一、ARIMA模型基本概念
1.1 自回归模型(AR)
- 描述当前值与历史值之间的关系,用变量自身的历史数据对自身进行预测;
- 自回归模型必须满足平稳性的要求;(何为平稳性:见时间序列数据分析基本概念)
- p阶自回归过程的公式定义:
其中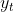是当前值,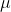是常数项,p是阶数,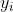是自相关系数,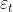是误差。
1.1.1 自回归模型的限制
- 自回归模型是用自身的数据来进行预测;
- 必须具有平稳性;
- 必须具有自相关性,如果自相关系数
小于0.5,则不宜采用;
- 自回归只适用于预测与自身前期相关的现象;
1.2 移动平均模型(MA)
- 移动平均模型关注的是自回归模型中的误差项的累加;
- 移动平均法能有效的消除预测中的随机波动;
- q阶自回归过程的公式定义:
1.3 自回归移动平均模型(ARMA)
自回归与移动平均的结合,公式定义:
1.4 差分自回归移动平均模型(ARIMA)
ARIMA(p,d,q)模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)
- AR是自回归,p为自回归项;MA为移动平均,q为移动平均项,d为时间序列成为平稳时所做的差分次数;
- 原理:将非平稳时间序列转化为平稳时间序列,然后因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型;
1.5 自相关函数ACF(autocorrelation function)
- 有序的随机变量序列与自身相比较,自相关函数反映了同一序列在不同时序的取值之间的相关性;
- 公式:
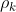的取值范围为[-1,1]。
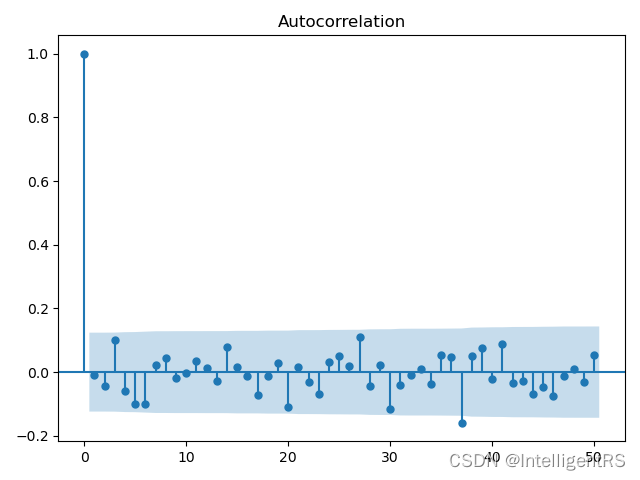
1.6 偏自相关函数PACF(partial autocorrelation function )
- 对于一个平稳AR(p)模型,求出滞后k自相关系数p(k)时,实际上得到的并不是x(t)与x(t-k)之间单纯的相关关系;
- x(t)同时还会受到中间k-1个随机变量x(t-1),x(t-2),...,x(t-k+1)的影响,而这k-1个随机变量又都和x(t-k)具有相关关系,所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响
- 剔除了中间k-1个随机变量x(t-1),x(t-2),...,x(t-k+1)的干扰之后x(t-k)对x(t)影响的相关程度;
- ACF还包含了其他变量的影响,而偏自相关系数PACF是严格这两个变量之间的相关性;
1.7 ARIMA(p,d,q)阶数确定
AR(p)看PACF,MA(q)看ACF
模型ACFPACFAR(p)衰减趋于零(几何型或振荡型)p阶后截尾MA(q)q阶后截尾衰减趋于零(几何型或振荡型)ARMA(p,q)q阶后衰减趋于零(几何型或振荡型)p阶后衰减趋于零(几何型或振荡型)
截尾:落在置信区间内(95%的点都符合该规则)
1.8 ARIMA建模流程
- 获取被观测系统时间序列数据;
- 对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
- 经过第二步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF ,通过对自相关图和偏自相关图的分析,得到最佳的阶层 p 和阶数 q;
- 由以上得到的 ,得到ARIMA模型。然后开始对得到的模型进行模型检验。
1.9 模型选择AIC与BIC:选择更简单的模型
- AIC:赤池信息准则(Akaike Information Criterion,AIC)
- BIC:贝叶斯信息准则(Bayesian Information Criterion,BIC)
k为模型参数个数,n为样本数量,L为似然函数;在保证模型精度的情况下尽量使得k值越小越好。
1.10 模型残差检验
- ARIMA模型的残差是否是平均值为0且方差为常数的正态分布;
- QQ图:线性即正态分布;
二、pandas数据处理
2.1 pandas数据重采样
date_range
- 可以指定开始时间与周期
- H:小时
- D:天
- M:月
import pandas as pd
import numpy as np
rng = pd.date_range("2016/07/01",periods=10,freq="D")
print(rng)

time = pd.Series(np.random.randn(20),index=pd.date_range("2016/1/1",periods=20))
print(time)
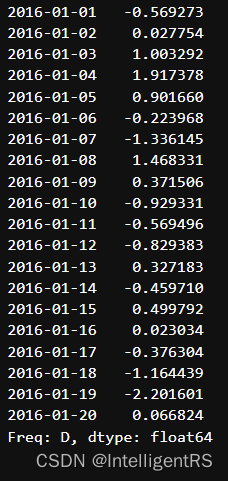
数据重采样:
- 时间数据由一个频率转换到另一个频率
- 降采样
- 升采样
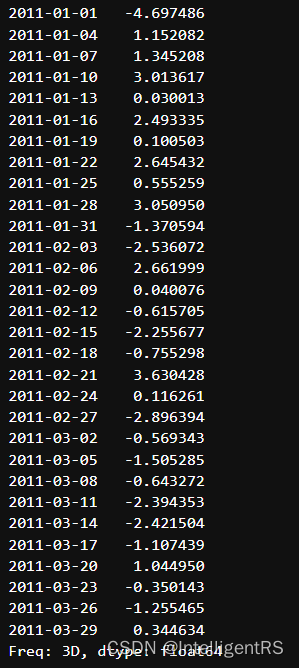
rng = pd.date_range("2011/1/1",periods=90,freq="D")
ts = pd.Series(np.random.randn(len(rng)),index=rng)
print(ts)
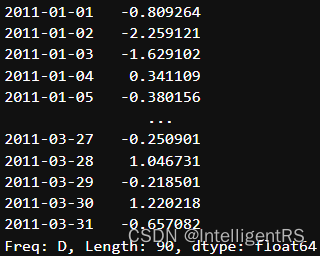
ts.resample("3D").sum()
升采样插值方法
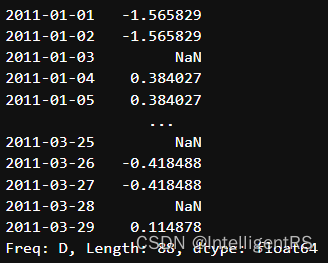
- ffill空值取前面的值
- bfill空值取后面的值
- interpolate 线性取值
day3D.resample("D").ffill(2)
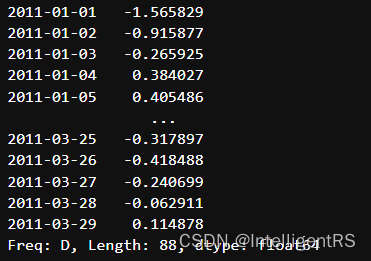
day3D.resample("D").interpolate("linear")
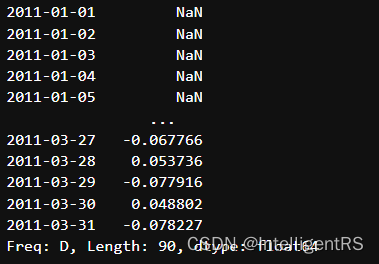
2.2 Pandas滑动窗口
r = ts.rolling(window=10).mean()
print(r)
import matplotlib.pyplot as plt
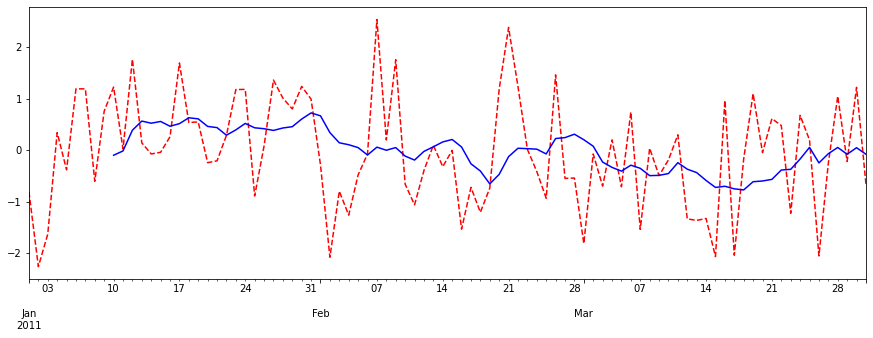
plt.figure(figsize=(15,5))
ts.plot(style="r--")
ts.rolling(window=10).mean().plot(style="b")
版权归原作者 IntelligentRS 所有, 如有侵权,请联系我们删除。