ID3 决策树的原理、构造及可视化（附完整源代码）

说明：

1、第一节至第三节来源于《机器学习及应用》李克清 时允田主编一书，大约在 57 页的位置。

2、源代码部分是我根据书中原理并参考源码后，自己重写。其中，源代码中的变量的定义对应第二节介绍的原理部分的数学符号，以便于适合对应学习。源代码中的注释是根据自己的理解所写。

3、本文是自己的学习过程的记录，还望读者海涵。如果有幸对大家产生帮助，不胜感激。

一、本文的问题定义和（决策树中）信息熵的回顾

① 本文的问题定义

②（决策树中）信息熵的回顾

（决策树中的）信息熵和样本分类的信息熵计算源代码_白白净净吃了没病的博客-CSDN博客本文包含（决策树）中的信息熵和实现源码，以及极为详细的注释和说明https://angxiao.blog.csdn.net/article/details/127156554

二、ID3 决策树的原理及构造

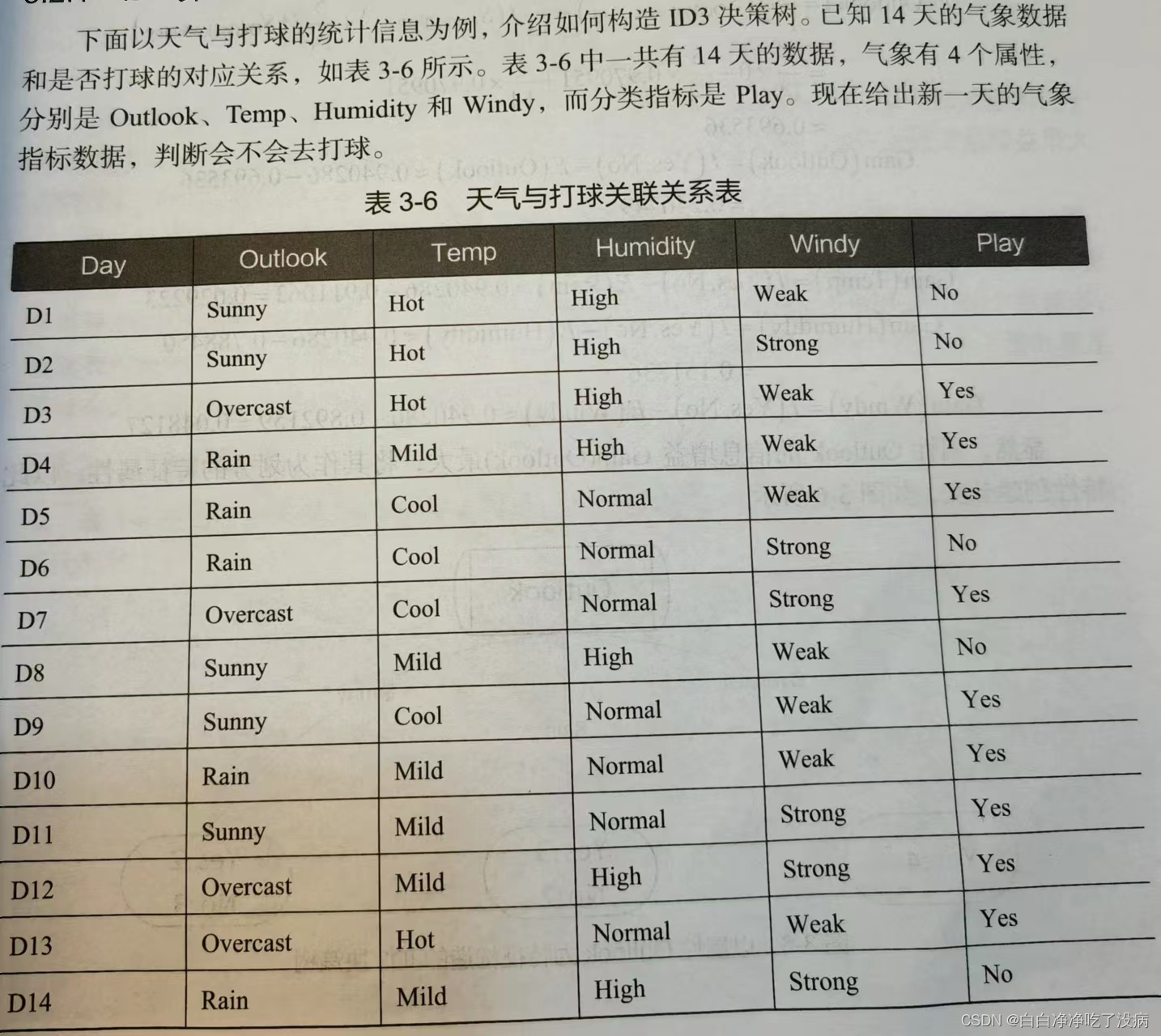
本文不写任何复杂通用的公式，以书中的例子作为本文的例子，个人觉得能够更通俗易懂：

继续对其他属性逐个计算信息增益，直到不能划分为止。在这个过程，不断找到具有最大信息熵的特征，采用递归思想来构造子树，最终构造出 ID3 的分类决策树。

三、ID3 决策树的可视化源码（含构造过程）

① main.py

from math import log2

# import treePlotter # 导入失败
import help  # 新建模块，然后导入

class ID3Tree(object):
    def __init__(self, data, cols):
        self.all_data = data  # 初始化数据集
        self.all_cols = cols  # 初始化数据集的各个列名（类别名）
        self.tree = {}  # 初始化ID3决策树

    def train(self):
        self.tree = self.make_tree(self.all_data, self.all_cols)

    def make_tree(self, data, cols):
        """
        :param data: 数据集：可能是总集，也可能是子集
        :param cols: 列名（特征名）：可能是全列名，也可能是当前数据集去掉最大信息熵特征后的列名集
        :return:树
        """
        all_label_datas = [item[-1] for item in data]  # 所有的标签对应的所有值
        # 1、如果这个数据集的全部标签都是一样的，那么没有属性划分的必要，决策树就一个叶子节点（即拿这个标签直接作为决策）
        if all_label_datas.count(all_label_datas[0]) == len(all_label_datas):
            return all_label_datas[0]
        # 2、如果这个数据集中每条数据（默认每条数据的长度和格式都一样）没有任何属性，只有标签
        # 我们看哪类标签出现的次数最多，直接拿它作为决策结果，这种情况决策树也就一个叶子结点
        elif len(data[0]) == 1:
            # 初始化出现的次数
            max_num = all_label_datas.count(all_label_datas[0])
            # 初始化出现次数最多的标签
            max_sort_data = all_label_datas[0]
            # set对原列表去重，但不改变原列表
            for i in list(set(all_label_datas)):
                if all_label_datas.count(all_label_datas[i]) > max_num:
                    max_num = all_label_datas.count(all_label_datas[i])
                    max_sort_data = i
            return max_sort_data
        # 3、正常情况，我们来构建决策树
        # *** 选取信息熵最大的属性（特征）***
        best_xns_feature_index = self.find_best_xns_feature(data)  # 找到香农熵最大的特征的下标
        best_feature_label = cols[best_xns_feature_index]  # 找到香农熵最大的特征的名称
        tree = {best_feature_label: {}}  # 构造一个（新的）树结点,一个根节点，大括号是子树
        del (cols[best_xns_feature_index])  # 删除数据集中香农熵最大的特征所在的列
        # 抽取最大增益的特征对应的列的数据
        best_xns_feature_values = [item[best_xns_feature_index] for item in data]
        for value in list(set(best_xns_feature_values)):
            # 此时的all_data是上次all_data去掉一列特征得到的
            sub_cols = cols
            sub_data = self.construct_new_dataset(data, best_xns_feature_index, value)
            # 递归构造子树
            tree[best_feature_label][value] = self.make_tree(sub_data, sub_cols)  # 向子树中放入值
        return tree

    def find_best_xns_feature(self, data):
        """
        计算各个特征的香农熵的大小，并返回香农熵最大的特征的下标
        :return: 香农熵最大的特征的下标
        """
        data_num = len(data)  # 数据集中样本的总数
        feature_nums = len(data[0]) - 1  # 数据集中所有特征的数量，-1是因为数据中不止有特征，还有标签
        I = self.calculate_xns(data)  # 数据集（样本标签）的香农熵
        best_xns_feature_value = 0  # 初始化香农熵最大的特征的值
        best_xns_feature_index = -1  # 初始化香农熵最大的特征的下标

        for i in range(feature_nums):
            feat_values = [number[i] for number in data]  # 得到某个特征列（随机变量）下的所有值
            feat_sorts = set(feat_values)  # 去重，得到特征的所有无重复的取值
            E = 0  # 初始化当前特征的信息熵
            # 对当前特征下具有相同特征值的子集，根据正负样本算出信息熵，并乘以prob。在不同特征值下计算完后，进行加和，得到E
            for value in feat_sorts:
                sub_dataset = self.construct_new_dataset(data, i, value)  # 得到i特征下，特征值为value的数据，去除特征i构成的集合
                prob = len(sub_dataset) / float(data_num)  # 特征i的值为value的数据所占的比例
                E += prob * self.calculate_xns(sub_dataset)
            # 用 I 减去 E，得到当前特征的信息增益gain
            gain = I - E  # 当前i特征的信息增益
            # 保留最大的信息熵及其对应的特征索引
            if gain > best_xns_feature_value:
                best_xns_feature_value = gain
                best_xns_feature_index = i

        return best_xns_feature_index  # 返回最大信息增益的特征的下标

    def construct_new_dataset(self, data, axis, value):
        """
        从数据集的某个特征中，选取值为某个特征值的数据，并去掉此特征，然后将这类数据构成新的数据集
        比如，在性别这个特征中，把特征值是男的数据抽出来，然后把这些数据的性别列去掉，构成数据集
        :param data:数据集
        :param axis:数据集中某个特征在数据中的索引
        :param value:此特征下的一个特征值
        :return:数据集中特征值是给定特征值的数据构成的子集
        """
        remain_dataset = []
        for item in data:  # 数据集中的每条数据
            if item[axis] == value:  # 如果这条数据的特征等于给定的某个特征值时
                # 把此条数据去掉这个特征列，重构此条数据
                remain_data = item[:axis]
                remain_data.extend(item[axis + 1:])
                remain_dataset.append(remain_data)  # 将重构后的数据加入列表中
        return remain_dataset

    def calculate_xns(self, data):
        """
        计算给定数据集的香农熵（信息熵）
        :return:数据集的香农熵
        """
        xns = 0.0  # 香农熵
        data_num = len(data)  # 样本集的总数，用于计算分类标签出现的概率

        # 将数据集样本标签的特征值（分类值）放入列表
        all_labels = [c[-1] for c in data]  # c[-1]：即取数据集中的每条数据的标签：Yes 或 No
        # print(all_labels)  # 得到 [Yes,No,No,...] 的结果
        # 按标签的种类进行统计，Yes这一类几个；No这一类几个
        every_label = {}  # 以词典形式存储每个类别（键）及个数（值）
        for item in list(set(all_labels)):  # 对每个类别计数，并放入词典, 其中set(all_labels) = [Yes,No]
            every_label[item] = all_labels.count(item)
        # 计算样本标签的香农熵，即数据集的香农熵
        for item2 in every_label:
            prob = every_label[item2] / float(data_num)  # 每个特征值出现的概率
            xns -= prob * log2(prob)  # xns是全局变量，这样就可以计算关于决策的要考虑的某个随机变量（如收入特征）的香农熵
        return xns

if __name__ == "__main__":
    dataset = [['sunny', 'hot', 'high', 'weak', 'NO'],
               ['sunny', 'hot', 'high', 'strong', 'NO'],
               ['overcast', 'hot', 'high', 'weak', 'YES'],
               ['rain', 'mild', 'high', 'weak', 'YES'],
               ['rain', 'cool', 'normal', 'weak', 'YES'],
               ['rain', 'cool', 'normal', 'strong', 'NO'],
               ['overcast', 'cool', 'normal', 'strong', 'YES'],
               ['sunny', 'mild', 'high', 'weak', 'NO'],
               ['sunny', 'cool', 'normal', 'weak', 'YES'],
               ['rain', 'mild', 'normal', 'weak', 'YES'],
               ['sunny', 'mild', 'normal', 'strong', 'YES'],
               ['overcast', 'mild', 'high', 'strong', 'YES'],
               ['overcast', 'hot', 'normal', 'weak', 'YES'],
               ['rain', 'mild', 'high', 'strong', 'NO']]
    # 前四列的名字（特征列）分别为天气、温度、湿度、风速
    labels = ['Outlook', 'Temp', 'Humidity', 'Windy']
    id3 = ID3Tree(dataset, labels)  # 实例化决策树对象
    id3.train()
    print(id3.tree)  # 输出决策树
    # treeplotter.createPlot(id3.tree) # 因treePlotter不能直接导入，这里会报错
    help.createPlot(id3.tree)  # 可视化决策树

    # 给定新一天的气象数据指标，根据决策树，来判断是否会去打球
    def predict_play(tree, new_dic):
        """
        根据构造的决策树，对未知数据进行预测
        :param tree: 决策树（根据已知数据构造的）
        :param new_dic: 一条待预测的数据
        :return:返回叶子节点，也就是最终的决策
        """
        while type(tree).__name__ == "dict":
            key = list(tree.keys())[0]
            tree = tree[key][new_dic[key]]
        return tree

    # 输出决策结果
    print(predict_play(id3.tree, {'Outlook': 'rain', 'Temp': 'mild', 'Humidity': 'high', 'Windy': 'weak'}))

**② help.py **

由于 treePlotter这个模块一直导入失败，目前未知原因。因此使用并在 main.py 中导入以下这个模块，用于构建 ID3 决策树。

import matplotlib.pyplot as plt

"""绘决策树的函数"""
decisionNode = dict(boxstyle="sawtooth", fc="0.8")  # 定义分支点的样式
leafNode = dict(boxstyle="round4", fc="0.8")  # 定义叶节点的样式
arrow_args = dict(arrowstyle="<-")  # 定义箭头标识样式

# 计算树的叶子节点数量
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs

# 计算树的最大深度
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth

# 画出节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center",
                            bbox=nodeType, arrowprops=arrow_args)

# 标箭头上的文字
def plotMidText(cntrPt, parentPt, txtString):
    lens = len(txtString)
    xMid = (parentPt[0] + cntrPt[0]) / 2.0 - lens * 0.002
    yMid = (parentPt[1] + cntrPt[1]) / 2.0
    createPlot.ax1.text(xMid, yMid, txtString)

def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.x0ff + \
              (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.y0ff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.y0ff = plotTree.y0ff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.x0ff = plotTree.x0ff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.x0ff, plotTree.y0ff), cntrPt, leafNode)
            plotMidText((plotTree.x0ff, plotTree.y0ff), cntrPt, str(key))
    plotTree.y0ff = plotTree.y0ff + 1.0 / plotTree.totalD

def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.x0ff = -0.5 / plotTree.totalW
    plotTree.y0ff = 1.0
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()

四、ID3 决策树可视化的效果及测试结果

① ID3 决策树可视化的效果

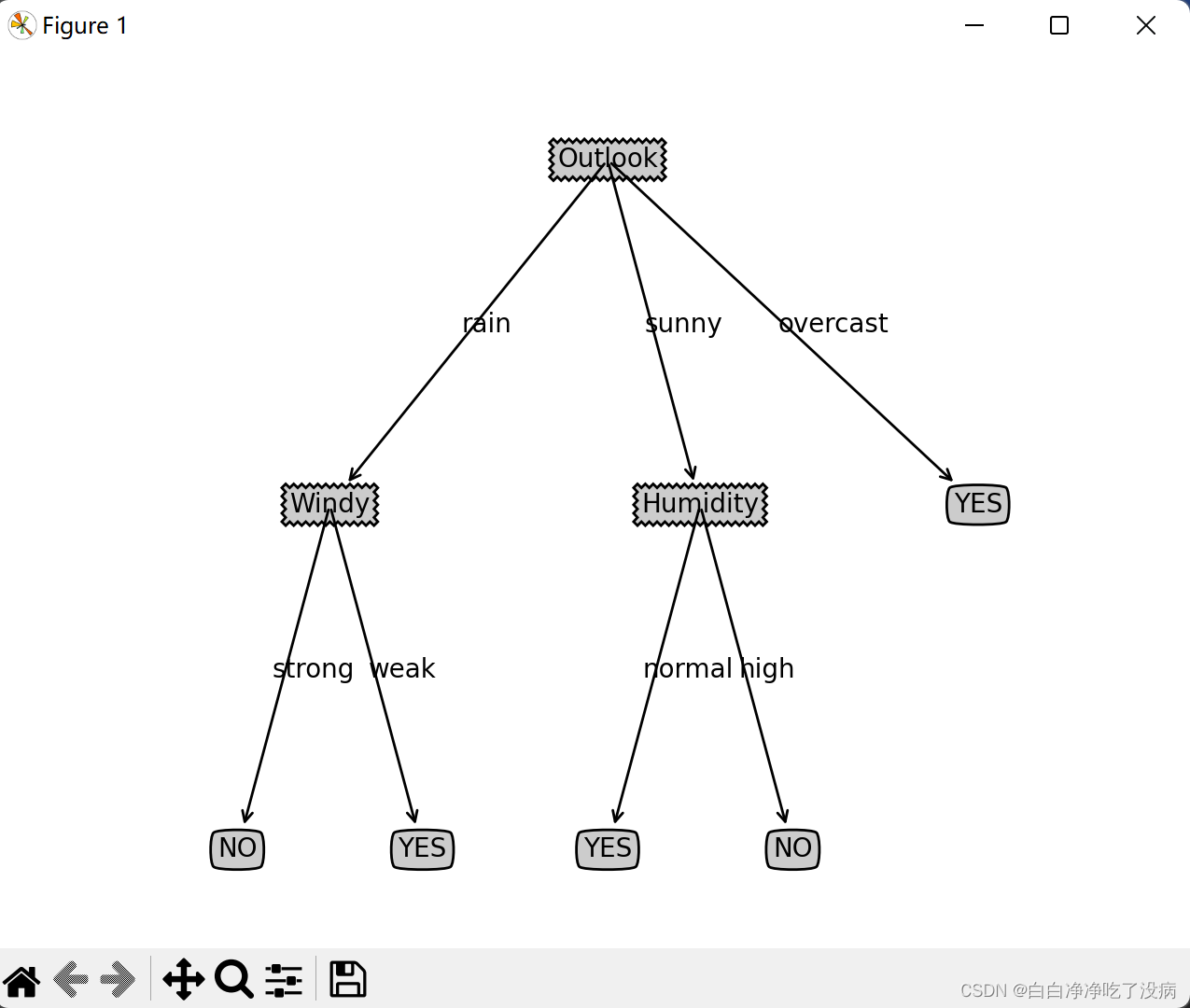
② ID3 决策树的文本化结果和用例的测试结果

五、ID3 算法的优缺点

ID3 算法是决策树的经典构建算法，它根据信息增益来评估和选择特征进行划分，每次选择信息增益最大的特征作为判断的模块（即特征节点），可用于划分标称型数据集（即数据中没有缺省特征值的数据集），虽然 ID3 比较灵活方便，但是有以下几个缺点：

（1）采用信息增益进行分裂，缺少剪枝的过程，很可能会出现过拟合的问题。我们可以合并相邻的无法产生大量信息增益的叶子结点（如设置信息增益阈值）。

（2）信息增益和属性的值域范围成正比，也就是有些特征（属性）取值很多，ID3算法很大可能将其作为分裂属性，导致分裂的精确度可能没有采用信息增益率进行分裂高。

（3）不能处理连续分布的数据特征，只能通过将连续性数据转化为离散型数据来解决，也不能处理数据集中的缺省值。