【Deep-sort多目标跟踪流程及其改进方法的解读】

【Deep-sort多目标跟踪流程及其改进方法的解读】

文前白话

• 本文针对deepsort的多目标跟踪方法进行梳理，了解其主要的流程步骤，以及相比于 sort 算法的改进原理进一步理解。

相关的文章、资源链接

• deepsort 开源代码连接与论文： 论文地址：https://arxiv.org/pdf/1703.07402.pdf. 代码地址：https://github.com/nwojke/deep_sort.
• 一些原理上解读的文章
• 1、DeepSORT（工作流程）.
• 2、DeepSort论文学习.
• 3、论文翻译：Deep SORT.
• 4、关于 Deep Sort 的一些理解.
• 5、目标追踪—deepsort原理讲解.
• 代码解读文章：
• 6、Deep sort算法代码解读（很详细）.

流程及其改进方法的梳理

一、多目标跟踪的流程

1. 获取原始视频帧，利用目标检测器对视频帧中的目标进行检测
2. 将检测到的目标的框中的特征提取出来，该特征包括表观特征（方便特征对比避免ID switch）和运动特征（运动特征方便卡尔曼滤波对其进行预测）
3. 计算前后两帧目标之前的匹配程度（利用匈牙利算法和级联匹配），为每个追踪到的目标分配ID。

二、Sort 与 deepSort 的对比

• sort算法的核心是卡尔曼滤波算法和匈牙利算法。
• 卡尔曼滤波：该算法的主要作用就是当前的一系列运动变量去预测下一时刻的运动变量，但是第一次的检测结果用来初始化卡尔曼滤波的运动变量。
• 匈牙利算法：简单来讲就是解决分配问题，就是把一群检测框和卡尔曼预测的框做分配，让卡尔曼预测的框找到和自己匹配的检测框，达到追踪的效果。
• DeepSort是在Sort目标追踪基础上的改进的，引入了在行人重识别的深度学习模型，在实时目标追踪过程中，提取目标的表观特征进行最近邻匹配，可以改善有遮挡情况下的目标追踪效果。同时，也减少了目标ID跳变的问题。

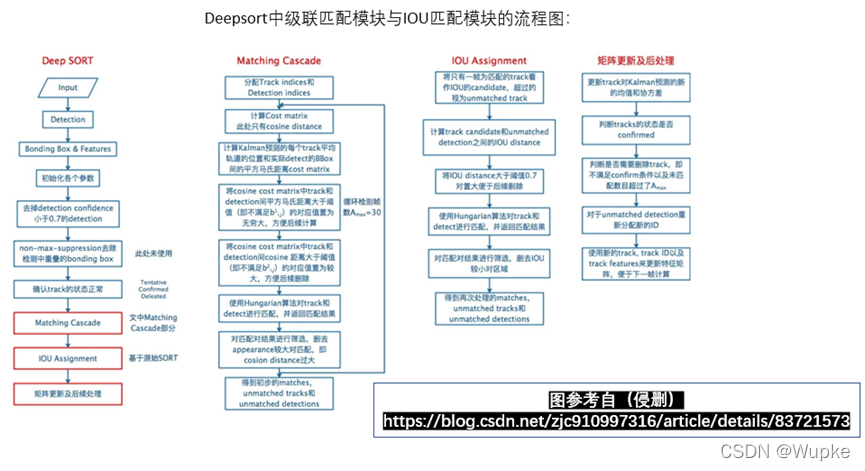
三、DeepSort主要的跟踪流程

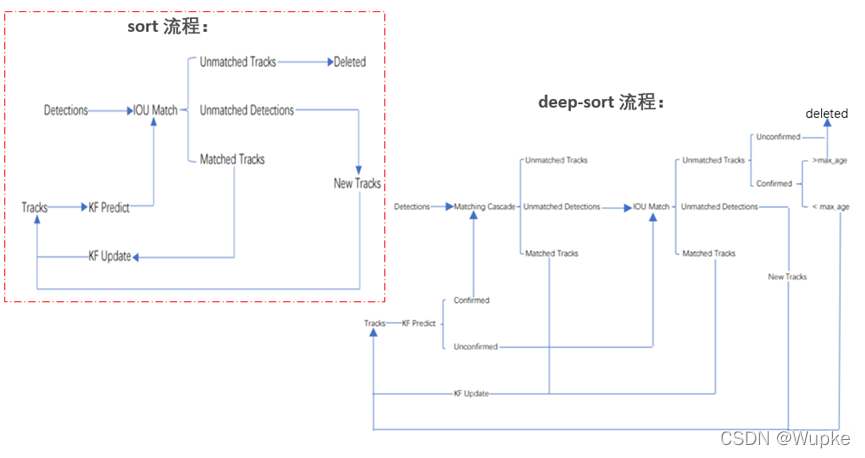
• （1）将初始的第一帧次检测到的结果创建其对应的Tracks，并通过卡尔曼滤波进行检测目标运动变量初始化，通过卡尔曼滤波预测其对应的框（最开始的Tracks是unconfirmed的）。
• （2）将该帧目标检测的框框和第上一帧通过Tracks预测的框框一一进行IOU匹配，再通过IOU匹配的结果计算其代价矩阵（cost matrix，其计算方式是1-IOU）。
• （3）将第（2）步中得到的所有的代价矩阵作为匈牙利算法的输入，得到线性的匹配的结果：得到的结果可能有三种：① Tracks失配（Unmatched Tracks），直接将失配的Tracks（默认连续达30次）删除； ② Detections失配（Unmatched Detections），则将这样的Detections初始化为一个新的Tracks（new Tracks）； ③ 检测框和预测的框框配对成功，这说明前一帧和后一帧追踪成功，将其对应的Detections通过卡尔曼滤波更新其对应的Tracks变量。
• （4）反复循环（2）-（3）步骤，直到出现确认态（confirmed）的Tracks或者视频帧结束。
• （5）通过卡尔曼滤波预测其确认态的Tracks和不确认态的Tracks对应的框框。将确认态的Tracks的框框和是Detections进行级联匹配（之前每次只要Tracks匹配上都会保存Detections其的外观特征和运动信息，默认保存前100帧，利用外观特征和运动信息和Detections进行级联匹配（提高Tracks和Detections匹配的性能））。
• （6）进行级联匹配后有三种可能的结果：① Tracks匹配，这样的Tracks通过卡尔曼滤波更新其对应的Tracks变量。 ② 第2、3种是Detections和Tracks失配，这时将之前的不确认状态的Tracks和失配的Tracks一起和Unmatched Detections一一进行IOU匹配，再通过IOU匹配的结果计算其代价矩阵。
• （7）将（6）中得到的所有的代价矩阵作为匈牙利算法的输入，得到线性的匹配的结果，这时候我们得到的结果有三种：①Tracks失配（Unmatched Tracks），直接将失配的Tracks（默认连续达30次）删除 ；② Detections失配（Unmatched Detections），将这样的Detections初始化为一个新的Tracks（new Tracks）。③ 检测框和预测的框框配对成功，这说明前一帧和后一帧追踪成功，将其对应的Detections通过卡尔曼滤波更新其对应的Tracks变量。
• （8）反复循环上述（5-7）步骤，直到视频帧结束。

四、关于DeepSort中部分模块原理的理解

• DeepSort中使用了递归的卡尔曼滤波和逐帧的数据关联，使用的跟踪思路：detection + track。代码实现过程中，检测的主要部分为输入：bounding box、confidence、feature等等。
• confidence主要用于进行一部分的检测框的筛选；bounding box与feature（ReID）用于后面与跟踪器的match匹配计算。

1、预测模块

• 运动状态估计描述：预测模块中会对跟踪器使用卡尔曼滤波器进行预测，使用的是卡尔曼滤波器的匀速运动和线性观测模型（有四个量且在初始化时会使用检测器进行恒值初始化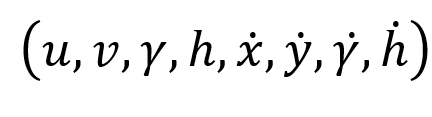）。 用上述状态参量来描述运动状态估计：其中(u,v)是bounding box的中心坐标，r是长宽比，h表示高度。其余四个变量表示对应的在图像坐标系中的速度信息。使用一个基于常量速度模型和线性观测模型的标准kalman滤波器进行目标运动状态的预测，预测的结果为(u,v,r,h)。
• 跟踪目标的创建与移除 对每一个追踪目标，记录自其上一次检测结果与追踪结果匹配之后的帧数a_k，一旦一个目标的检测结果与追踪结果正确关联之后，就将该参数设置为0。如果a_k超过了设置的最大阈值A_max，则认为对该目标的追踪过程已结束。对新目标出现的判断则是，如果某次检测结果中的某个目标始终无法与已经存在的追踪器进行关联，那么则认为可能出现了新目标。如果连续的3帧中潜在的新的追踪器对目标位置的预测结果都能够与检测结果正确关联，那么则确认是出现了新的运动目标；如果不能达到该要求，则要删除该运动目标。

2、更新模块

在更新模块中也包括匹配，追踪器更新与特征集更新。在更新模块的部分，根本的方法还是使用IOU来进行匈牙利算法的匹配，在此基础上添加了新的关联方法。传统的解决检测结果与追踪预测结果的关联的方法是使用匈牙利方法。Deepsort中同时考虑了运动信息的关联和目标外观信息的关联。

• 运动信息的关联：使用了对已存在的运动目标的运动状态的kalman预测结果与检测结果之间的马氏距离和余弦距离进行运行信息的关联。
• 马氏距离关联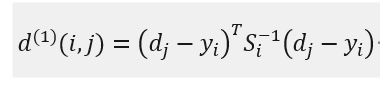： 其中， d_j表示第j个检测框的位置，y_i表示第i个追踪器对目标的预测位置，S_i表示检测位置与平均追踪位置之间的协方差矩阵。马氏距离通过计算检测位置和平均追踪位置之间的标准差将状态测量的不确定性进行了考虑。如果某次关联的马氏距离小于指定的阈值t_(1)则设置运动状态的关联成功。使用的函数为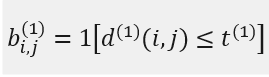： 如果上面的距离小于指定的阈值，那么这个关联就是成功的。阈值是从单独的训练集里得到的。（论文中阈值t^((1))=9.4877）
• 当运动的不确定性很低的时候，上述的马氏距离匹配是一个合适的关联度量方法，但是在图像空间中使用kalman滤波进行运动状态估计只是一个比较粗糙的预测。特别是相机存在运动时会使得马氏距离的关联方法失效，造成出现ID- switch的现象。因此作者引入了第二种关联方法-》余弦距离：

对每一个的检测块d_j求一个特征向量r_i,限制条件是∣r_i∣ = 1.对每一个追踪目标构建一个gallary，存储每一个追踪目标成功关联的最近100帧的特征向量。第二种度量方式就是计算第i个追踪器的最近100个成功关联的特征集与当前帧第j个检测结果的特征向量间的最小余弦距离。计算公式为：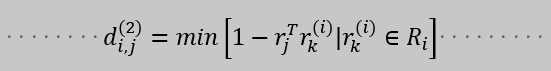

如果上面的距离小于指定的阈值，那么这个关联就是成功的。阈值是从单独的训练集里得到的。

• 最终使用两种度量方式的线性加权作为最终的度量Ｃij（如果在两个度量阈值都满足了才能用于融合Ｃij,），位于两种度量阈值的交集内时，才认为实现了正确的关联。
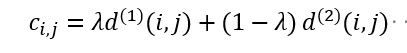
• 距离度量对短期的预测和匹配效果很好，但对于长时间的遮挡的情况，使用外观特征的度量比较有效。
• 对于存在相机运动的情况，可以设置 λ=0. 但是，马氏距离的阈值仍然生效，如果不满足第一个度量的标准，就不能进入Ｃij的融合阶段。

3、使用级联匹配算法

针对每一个检测器都会分配一个跟踪器，每个跟踪器会设定一个time_since_update参数。如果跟踪器完成匹配并进行更新，那么参数会重置为0，否则就会+1。实际上，级联匹配换就是不同优先级的匹配。在级联匹配中，会根据这个参数来对跟踪器分先后顺序，参数小的先来匹配，参数大的后匹配。也就是给上一帧最先匹配的跟踪器高的优先权，给好几帧都没匹配上的跟踪器降低优先权（逐渐降低）。至于使用级联匹配的目的，引用文章（- 3、论文翻译：Deep SORT.）里的解释：

当一个目标长时间被遮挡之后，kalman滤波预测的不确定性就会大大增加，状态空间内的可观察性就会大大降低。假如此时两个追踪器竞争同一个检测结果的匹配权，往往遮挡时间较长的那条轨迹的马氏距离更小，使得检测结果更可能和遮挡时间较长的那条轨迹相关联，这种不理想的效果往往会破坏追踪的持续性。可以理解为，假设本来协方差矩阵是一个正态分布，那么连续的预测不更新就会导致这个正态分布的方差越来越大，那么离均值欧氏距离远的点可能和之前分布中离得较近的点获得同样的马氏距离值。所以，作者使用了级联匹配来对更加频繁出现的目标赋予优先权。

4、马氏距离与余弦距离的添加

这两种距离，实际上是针对运动信息与外观信息的计算。
马氏距离就是“加强版的欧氏距离”。它实际上是规避了欧氏距离中对于数据特征方差不同的风险，在计算中添加了协方差矩阵，其目的就是进行方差归一化，从而使所谓的“距离”更加符合数据特征以及实际意义。马氏距离是对于差异度的衡量中，的一种距离度量方式，而不同于马氏距离，余弦距离则是一种相似度度量方式。前者是针对于位置进行区分，而后者则是针对于方向。使用余弦距离的时候，可以用来衡量不同个体在维度之间的差异，而一个个体中，维度与维度的差异我们却不好判断，此时我们可以使用马氏距离进行弥补，从而在整体上可以达到一个相对于全面的差异性衡量。而我们之所以要进行差异性衡量，根本目的也是想比较检测器与跟踪器的相似程度，优化度量方式，也可以更好地完成匹配。

5、添加的深度学习特征

这部分是属于ReID模块，也是deepsort的主要更新改进的地方。deepsort在对于sort的改进中加入了一个深度学习的特征提取网络，作者将所有confirmed的追踪器（其中一个状态）每次完成匹配对应的detection的feature map存储进一个list。存储的数量作者使用budget超参数（100帧）进行限制（如果实时性效果不好的话，可以尝试调低这个参数加快速度）。从而在每次匹配之后都会更新这个feature map的list，比如去除掉一些已经出镜头的目标的特征集，保留最新的特征将老的特征 pop 掉等等。这个特征集在进行余弦距离计算的时候将会发挥作用。实际上，在当前帧，会计算第i个物体跟踪的所有Feature向量和第j个物体检测之间的最小余弦距离。

6、IOU 计算 与匈牙利算法匹配

这个方法是在sort中被提出的，实际上匈牙利算法可以理解成“尽量多”的一种思路，比如说A检测器可以和a，c跟踪器完成匹配（与a匹配置信度更高），但是B检测器只能和a跟踪器完成匹配。那在算法中，就会让A与c完成匹配，B与a完成匹配，而降低对于置信度的考虑。所以算法的根本目的并不是在于匹配的准不准，而是在于尽量多的匹配上，这是在deepsort中添加级联匹配与马氏距离与余弦距离的根本目的，因为仅仅使用匈牙利算法进行匹配特别容易造成ID switch，就是一个检测框id不停地进行更换，缺乏准确性与鲁棒性。针对匹配的置信度高这一标准，作者是使用IOU进行衡量，计算检测器与跟踪器的IOU，将这个作为置信度的高低。