Identification
当我们以因果结构图模型的形式捕获了我们的因果假设,因果分析的第二个阶段就是识别。在这个阶段,我们的目标是分析我们的因果模型——包括特征之间的因果关系以及观察到哪些特征——以确定我们是否有足够的信息来回答特定的因果推断问题。
我们首先使用干预图来形式化因果推理问题的概念。我们描述了将干预图中的关系与我们观察数据的因果模型联系起来的do-calculus规则。我们展示了do-calculus如何引导我们各种识别策略,以及do-calculus如何与参数假设相结合。最后,我们讨论了这些策略的相对优势和劣势,并讨论了分析因果推理问题的常用方法,以帮助从这些不同的方法中进行选择。
Causal inference quesitons: Concepts and Notation
在这里我们缩小范围讨论因果推理问题,讨论这些问题需要的假设有:(1)因果模型是已知的。(2)我们希望量化两个特定变量之间的因果关系,例如他的强度和函数关系。因果模型,无论是以图形形式还是以一组等式表达,都捕捉了我们对节点之间可能存在的关系的假设。
Formalizing causal inference questions using intervention graphs and do notation

图 1
基于图1的因果图,我们所存在的疑惑就是干预如何改变特征A的值影响特征B的值?我们不能简单地称之为
P
(
B
∣
A
)
P(B|A)
P(B∣A),因为这个符号已经用来表示观察到的分布,这是有变量C参与的情况下得出的分布结果,这是统计关系。在我们观察到的数据中,我们所期望的是 B 的值会是什么在给定一个特定的A的值情况下。
为了正确地表述这个问题,我们必须首先引入一种符号,来处理统计关系和因果关系之间的微妙区别。为了表示A和B的因果关系,我们需要一个特殊的数学符号来将它与数学上的统计关系做一个区分。我们把这种因果关系写成:
P
(
B
∣
d
o
(
A
)
)
P(B|do(A))
P(B∣do(A))
d
o
(
A
)
do(A)
do(A)符号表示在变量A上所做的干预,当我们估计 B 以
d
o
(
A
)
do(A)
do(A)为条件 ,我们想象自己改变了变量A地值,同时保持其余部分不变——当然,直接或间接的变化来自于操纵 A 的值。因为我们的干预是独立于系统的其余部分进行的,所以我们本质上是在创造一个新的因果模型,我们已经切断了这个模型 A 来自其所有父代的边。换句话说,我们的情况如图2所示。换句话说我们看到了原始的图G,图2的右边我们看到了具有该特征的相同模型 A 现在是独立确定的。称图2为介入干预图或者
D
o
G
r
a
p
h
Do Graph
DoGraph,
G
d
o
(
A
)
G_{do(A)}
Gdo(A)。这是一个新系统,如果我们可以观察从数据分布中取样的数据
P
∗
P^*
P∗对应于这个新系统,我们观察到的数据将完美地代表两者之间的因果关系 A 和其他值。也就是说
P
(
B
∣
d
o
(
A
)
)
=
P
∗
(
B
∣
A
)
P(B|do(A))=P^*(B|A)
P(B∣do(A))=P∗(B∣A)因此
E
[
B
∣
d
o
(
A
)
]
=
E
∗
[
B
∣
A
]
E[B|do(A)]=E^*[B|A]
E[B∣do(A)]=E∗[B∣A]。
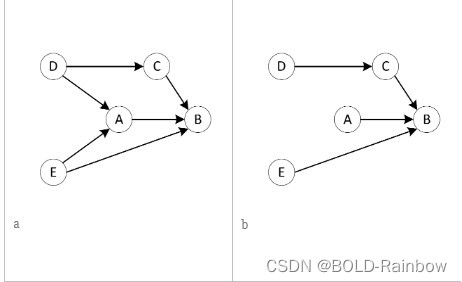
图2
由于在需要做出决策的背景下我们需要经常问出因果性质的问题,而且我们经常比较两种可能性的结果来帮助我们理解我们可能采取的行动措施。例如,加入我们计划在变量A上实施一个干预措施,我们因果推断问题就关注在比较A=1和A=0的效果。所以
A
→
B
A\:\rightarrow\:B
A→B的因果效应表示为:
P
(
B
∣
d
o
(
A
=
1
)
)
−
P
(
B
∣
d
o
(
A
=
0
)
)
(1)
P(B|do(A=1))\:-\:P(B|do(A=0))\tag{1}
P(B∣do(A=1))−P(B∣do(A=0))(1)
当然,如果我们决策的重点比较复杂,涉及多个选项,我们会在选项之间做很多比较。
如果我们决策的焦点是一个连续变量,我们可以用导数来表示干预的效果:
d
B
d
d
o
(
A
)
=
lim
Δ
→
0
[
P
(
B
∣
d
o
(
A
+
Δ
A
)
−
P
(
B
∣
d
o
(
A
)
)
Δ
A
]
(2)
\frac{dB}{d \:do(A)}=\lim_{\Delta\rightarrow0}[\frac{P(B|do(A\:+\:\Delta A)\:-\:P(B|do(A))}{\Delta A}\tag{2}]
ddo(A)dB=Δ→0lim[ΔAP(B∣do(A+ΔA)−P(B∣do(A))](2)
或者,如果有多个独立变量,我们可以将影响写成偏导数,其中偏导数的计算是
X
X
X,排除治疗的独立变量的集合。
∂
B
∂
d
o
(
A
)
=
lim
Δ
A
→
0
[
P
(
B
∣
d
o
(
A
+
Δ
A
)
,
X
)
−
P
(
B
∣
d
o
(
A
)
,
X
)
Δ
A
]
(3)
\frac{\partial B}{\partial do(A)}=\lim_{\Delta A \rightarrow 0}[\frac{P(B|do(A\:+\:\Delta A),X)-P(B|do(A),X)}{\Delta A}]\tag{3}
∂do(A)∂B=ΔA→0lim[ΔAP(B∣do(A+ΔA),X)−P(B∣do(A),X)](3)
Feature Interactions and Heterogeneous Effects
治疗对结果的影响很少是简单和一致的。更确切地说,这种效果通常会因上下文或单元级特性而异。例如,一个医疗程序在年轻或年老的病人身上可能效果更好或更差;或者,价格折扣可能会增加某些产品的销量,但不会增加其他产品的销量。
我们将这些不同的效果建模为特征交互。在我们的系统图形模型中,我们的结果特征将具有来自治疗的传入边缘,以及一个或多个影响结果或修改治疗对结果的影响的上下文特征。例如,图2中结果变量B不仅有来自变量A的入度也同时包括有来自其他变量C和E的入度。这些变量可能会和A相互作用进而削弱或者扩大对结果变量B的影响。仅从因果图看我们不知道变量C和E如何影响A来改变B。
回想一下,我们可以将节点的值表示为其父特性的一般函数。不失一般性,让我们将节点的值表示为单个父节点的一般函数,
v
0
v_0
v0和剩余父节点的向量
v
v
v :
f
(
v
0
,
v
)
f(v_0,v)
f(v0,v)。如果变量
v
0
v_0
v0的边
e
0
e_0
e0和其他结点变量没有互相作用,那么
v
0
v_0
v0的效果是同质的,我们可以分解
f
(
v
0
,
v
)
f(v_0,v)
f(v0,v)为:
f
(
v
0
,
v
)
=
ϕ
(
g
0
(
v
0
)
+
g
1
(
v
)
)
f(v_0,v)=\phi (g_0(v_0)\: + \:g_1(v))
f(v0,v)=ϕ(g0(v0)+g1(v));如果
v
0
v_0
v0确实和其他结点有交集,那么
v
0
v_0
v0的结果就是异质的那么
f
(
v
0
,
v
)
f(v_0,v)
f(v0,v)就会被分解为
f
(
v
0
,
v
)
=
ϕ
(
g
0
(
v
0
,
v
′
)
+
g
1
(
v
)
)
f(v_0,v)=\phi (g_0(v_0,v')\: +\:g_1(v))
f(v0,v)=ϕ(g0(v0,v′)+g1(v)),其中
v
′
v'
v′是
v
v
v的子集,有时也称
v
′
v'
v′是结果修改器。
将异质效应与同质效应可用公式表述为,如果异质:
P
(
Y
∣
d
o
(
v
0
)
)
≠
P
(
Y
∣
d
o
(
v
0
,
v
)
)
P(Y|do(v_0)) \neq P(Y|do(v_0,v))
P(Y∣do(v0))=P(Y∣do(v0,v));如果同质:
P
(
Y
∣
d
o
(
v
0
)
=
P
(
Y
∣
d
o
(
v
0
,
v
)
)
P(Y|do(v_0)\:=\:P(Y|do(v_0,v))
P(Y∣do(v0)=P(Y∣do(v0,v))
在识别因果关系时如何考虑结果修改器? 在某些情况下,我们可能只对给定已知人口分布的治疗的平均因果效应感兴趣。例如,我们可以根据平均因果效应1来决定是否应用全局处理。有趣的是,估计平均因果效应并不一定需要测量因果修改器。也就是说,只要它们不是混杂因素,它们可能不会被观察到。然而,我们必须记住,如果我们测量一个人口分布的平均效应,如果人口发生变化,它将不再有效。
在大多数情况下,我们的总体任务目的将要求我们捕捉因果效应的全部分布;也就是说,我们必须了解治疗效果如何随着那些结果修改器的变化而变化。个体治疗效果(ITE)是对特定个体单位和环境的治疗效果的估计。请注意,ITE做出了一个强有力的假设,即所有的效果修改器都是已知的,并且在模型中被捕获,并且也被观察到。如果我们认为可能存在未知或未观察到的结构修正变量,那么更正确的说法是我们正在识别条件平均治疗效应(CATE)。
此外,我们有时会计算局部平均治疗效果(local-ATE)。Local-ATE是对治疗效果的估计,但仅针对特定的亚群或效果修正值的子集。
Direct and mediated Effects
在因果图中,可能有多条路径,通过这些路径,改变某些特征可以影响我们关心的某些结果。例如在图2 a中,改变变量E的值可通过边E
⇒
\Rightarrow
⇒B直接影响B;间接地,改变变量E通过中间变量A间接影响变量A,
E
⇒
A
⇒
B
E\Rightarrow A \Rightarrow B
E⇒A⇒B。通常,当我们希望衡量和理解某个特征对结果的影响时,我们希望知道该特征对结果的总体影响,不管这种影响是直接的还是间接的。
有时区分直接效应和间接效应是有用的。例如,当我们在分析一个涉及长期结果的情况时,测量一个中介的短期结果可能是有用的,以了解我们的变化正在产生什么影响。在其他情况下,理解影响如何通过中介路径传播,可能会让我们深入了解如何更好地控制这些影响。例如,我们也许能够找到阻断一些路径的方法来防止负面影响。
理论上说,这个
P
(
Y
∣
d
o
(
T
)
)
P(Y|do(T))
P(Y∣do(T))符号表示治疗变量在结果变量上的效果。假如,在治疗变量T和结果变量Y之间给定k个中间变量,其中每个中间变量都有单个特征
m
1...
k
m_{1...k}
m1...k我们可以计算治疗变量T到结果变量Y的
m
i
m_i
mi中介效应
M
E
i
=
P
(
Y
∣
d
o
(
m
i
)
P
(
m
i
∣
d
o
(
T
)
)
)
ME_i=P(Y|do(m_i)P(m_i|do(T)))
MEi=P(Y∣do(mi)P(mi∣do(T))),这种链式计算可以扩展到由多个中间变量组成的更长中间路径。
治疗变量T在结果变量Y的因果效应与各个中间变量的因果效应的 和 差异是:
d
i
r
e
c
t
e
f
f
e
c
t
=
P
(
Y
∣
d
o
(
T
)
)
−
∑
i
=
1...
k
M
E
i
(4)
direct\: effect=P(Y|do(T))\: - \: \sum_{i=1...k}ME_i \tag{4}
directeffect=P(Y∣do(T))−i=1...k∑MEi(4)
Do calculus
因果识别的任务是确定一个表达式,即因果估计,它将我们的目标值表达为我们系统中可观察到的相关关系的函数。也就是说,如何表达
P
(
B
∣
d
o
(
A
)
)
P(B|do(A))
P(B∣do(A))——也就是干预图中A和B的相关性,作为初始图中可观察到的相关性函数。
Randomized Experiments
作为理解原始图和介入图之间的联系的起点,从考虑随机实验的因果图开始是比较容易的。当治疗变量 A 在实验中是随机的,它在图中没有祖先。如果我们画出干涉图,
d
o
(
A
)
do(A)
do(A),我们看到它和原文是一样的。因此,在
d
o
(
A
)
do(A)
do(A)的干预图中可以看出
P
(
B
∣
d
o
(
A
)
)
P(B|do(A))
P(B∣do(A))和条件概率
P
(
B
∣
A
)
P(B|A)
P(B∣A)是一样的。此外,这不需要分析因果图的其余部分,这意味着我们可以确定的因果关系 A 在不知道系统中的因果关系的情况下A是随机分配的。这种对因果系统知识的稳健性是为什么随机实验被认为是识别因果效应的黄金标准。
随机化可以来自许多来源。有时,随机化是系统逻辑的固有部分,例如在负载平衡算法中,随机地将传入的请求分配给一个可用的服务器。
当我们观察的系统不是随机实验时,我们该怎么办?我们如何确定一个因果估计来表示
P
(
B
∣
d
o
(
A
)
)
P(B|do(A))
P(B∣do(A))基于在非随机实验中观察到的混杂相关性?在下一节中,我们将描述可以帮助我们完成这项任务的规则演算。
Causal Distributions from Observational Data
我们现在的挑战,在我们分析的因果识别阶段,变得更加清晰。我们希望去计算
P
[
B
∣
d
o
(
A
)
]
P[B|do(A)]
P[B∣do(A)]的值,但是我们没有观察到系统中代表
G
d
o
(
A
)
G_{do(A)}
Gdo(A)的图。换句话说就是,以
P
G
d
o
(
A
)
(
⋅
)
P_{G_{do(A)}}(·)
PGdo(A)(⋅)为概率分布的数据是不可用的。所以我们应该去估计
P
G
d
o
(
A
)
[
B
∣
A
]
=
P
[
B
∣
d
o
(
A
)
]
P_{G_{do(A)}}[B|A]=P[B|do(A)]
PGdo(A)[B∣A]=P[B∣do(A)]。因此,我们必须确定一种策略,在只给定系统观测值的情况下计算这个值
G
G
G并从概率分布中取样
P
(
⋅
)
P(·)
P(⋅)。
正是因为我们没有来自
P
G
d
o
(
A
)
P_{G_{do(A)}}
PGdo(A)概率分布的数据,一个自然而然的策略是写出根据概率表达式
P
G
d
o
(
A
)
P_{G_{do(A)}}
PGdo(A)的数量。为此,我们可以利用一种干预(给定一个治疗变量T)对应于因果图中特定结构变化的事实,并找到在这种变化下应该保持不变的条件分布。具体而言,由于治疗变量仅影响到接受治疗的结果变量,因此其后代节点的结构方程应该保持不变,因此给定其父代的后代变量的条件分布应该保持不变。也就是说,假如变量B的父结点为
P
a
(
B
)
Pa(B)
Pa(B),那么我给定治疗变量A就不会影响变量B,式子表示为
P
G
d
o
(
A
)
(
B
∣
P
a
B
)
=
P
(
B
∣
P
a
B
)
P_{G_{do(A)}}(B|PaB)\: = \:P(B|PaB)
PGdo(A)(B∣PaB)=P(B∣PaB)。类比着,我们可以声称,观察数据分布中变量之间的任何条件独立性也应该适用于干预分布,因为干预只是从图中删除一些边,而不是添加它们。如果变量B在给定变量D的条件下独立的话,那么
P
(
B
∣
D
,
C
)
=
P
(
B
∣
D
)
P(B|D,C)\: = \:P(B|D)
P(B∣D,C)=P(B∣D)而且
P
G
d
o
(
A
)
(
B
∣
C
,
D
)
=
P
G
d
o
(
A
)
(
B
∣
D
)
P_{G_{do(A)}}(B|C,D)\: = \: P_{G_{do(A)}}(B|D)
PGdo(A)(B∣C,D)=PGdo(A)(B∣D)。
以上描述的属性应用我们在这里举个栗子:eg.
P
(
B
∣
d
o
(
A
)
)
P(B|do(A))
P(B∣do(A))其中
A
⊃
P
a
(
B
)
A \supset \: Pa(B)
A⊃Pa(B)也就是说变量B的父结点包含于变量A,那么应用到以上公式我们就可以得到。
P
(
B
∣
d
o
(
A
)
)
=
P
G
d
o
(
A
)
(
B
∣
A
)
=
P
G
d
o
(
A
)
(
B
∣
P
a
(
B
)
,
A
∖
P
a
(
B
)
)
=
P
G
d
o
(
A
)
(
B
∣
P
a
(
B
)
)
=
P
G
d
o
(
A
)
(
B
∣
P
a
(
B
)
)
\begin{aligned} P(B|do(A)) &= P_{G_{do(A)}}(B|A) \\ &= P_{G_{do(A)}}(B|Pa(B),A \setminus Pa(B)) \\ &= P_{G_{do(A)}}(B|Pa(B)) \\ &= P_{G_{do(A)}}(B|Pa(B)) \end{aligned}
P(B∣do(A))=PGdo(A)(B∣A)=PGdo(A)(B∣Pa(B),A∖Pa(B))=PGdo(A)(B∣Pa(B))=PGdo(A)(B∣Pa(B))
因此,从涉及do算子的目标概率表达式开始,我们能够仅基于观察到的概率分布来构建概率P的表达式 最终的表达式被称为识别的估计需求或目标估计需求,并且可以从可用数据中估计。将一个目标do表达式转换成一个只包含观察概率的表达式的过程称为识别。
do-calculus不是为每一个新的do表达式都提出这样的属性,而是为任何因果图概括上述过程的一套规则。do-calculus的关键优势在于,它将这种自定义推导形式化为一个通用框架,该框架可以机械地应用于任何图以及该图的任何因果推理问题。给定一个因果图,它允许我们将因果图中的概率(我们没有观察到)与我们可以在观察图中观察到的统计关系联系起来。也就是说,do-calculus将为我们提供转换因果目标的工具, $ P(B|do(A)$,到一个因果估计,可从观察数量计算。
Graph Rewriting
一个概率图G代表我们对一个系统的因果假设,它是有用的,能够根据参考该图G将之修改为因果图
G
d
o
G_{do}
Gdo.
-interventional Graph: 当我们确定了图并指定了图中的治疗变量比如变量A。那么图
G
d
o
(
A
)
G_{do(A)}
Gdo(A)可以说和原始概率图G相同,只不过将变量A的入度边(来自父结点)都移除了。
-Nullified Graph: 参考无效图也是有用的,在无效图中,我们人为地移除或无效了一个特征的所有效果 C。这种图我们称之为
G
n
u
l
l
(
C
)
G_{null(C)}
Gnull(C), 和图G相同来自变量C的出度边都被移除了。

图3
Rules of Do-calculus
do-calculus包含三个简单的规则:
insertion or deletion of observations P ( y ∣ d o ( x ) , z , ω ) = P ( y ∣ d o ( x ) , ω ) i f ( y ⊥ z ∣ x , ω ) G d o ( x ) P(y|do(x),z,\omega )=P(y|do(x),\omega )\quad\quad if(y\bot z|x,\omega){G{do(x)}} P(y∣do(x),z,ω)=P(y∣do(x),ω)if(y⊥z∣x,ω)Gdo(x) 规则1表明,我们可以从条件变量集中移除变量z,如果条件变量 ω \omega ω和治疗变量 x x x 在干预图中 d-separate也就是条件分离变量 y y y和 z z z。当然,我们也可以以相同的标准添加其他条件变量。规则1的概率图示应该是:

图4
Action/observation exchange P ( y ∣ d o ( x ) , d o ( z ) , ω ) = P ( y ∣ d o ( x ) , z , ω ) i f ( y ⊥ z ∣ x , ω ) G d o ( x ) , n u l l ( z ) P(y|do(x),do(z),\omega)=P(y|do(x),z,\omega) \quad\quad if(y \bot z|x,\omega){G{do(x),null(z)}} P(y∣do(x),do(z),ω)=P(y∣do(x),z,ω)if(y⊥z∣x,ω)Gdo(x),null(z) 规则2表明我们在图 G d o ( x ) , n u l l ( z ) G_{do(x),null(z)} Gdo(x),null(z)可以替换掉一个治疗变量 d o ( z ) do(z) do(z),也就是说如果给定变量 x x x 和 ω \omega ω,导致 y y y 和 z z z d-separation。其中我们移除了变量x的所有入度和变量z的所有出度。 为了理解这个规则,我们举个简单例子比如对变量x不施加干预: P ( y ∣ d o ( z ) , ω ) = p ( y ∣ z , ω ) G n u l l ( z ) P(y|do(z),\omega) = p(y|z,\omega){G{null(z)}} P(y∣do(z),ω)=p(y∣z,ω)Gnull(z) 在这个简单的例子当中,如果变量 y y y和变量 z z z在给定 ω \omega ω的条件下相互独立,其中z没有出度边,那么也就意味着变量z和y之间的连接是没有被 ω \omega ω阻挡的,(真实的连接情况应该是从变量z直接连接y)这个模型的简单草图应该是图4这样的。因此得到公式 P ( d o ( z ) . ω ) = P ( y ∣ z , ω ) P(do(z).\omega) = P(y|z,\omega) P(do(z).ω)=P(y∣z,ω)

图5
额外的干预变量
x
x
x遵循规则1的原则
insertion/deletion of actions P ( y ∣ d o ( x ) , d o ( z ) , ω ) = P ( y ∣ d o ( x ) , ω ) i f ( y ⊥ z ∣ x , ω ) G d o ( x ) d o ( z ( ω ) ) P(y|do(x),do(z),\omega)=P(y|do(x),\omega) \quad\quad if(y\bot z|x,\omega){G{do(x)do(z(\omega))}} P(y∣do(x),do(z),ω)=P(y∣do(x),ω)if(y⊥z∣x,ω)Gdo(x)do(z(ω)) 关于规则3的理解还是通过因果图来表示。
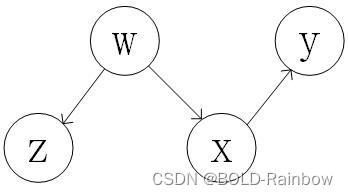
图6
版权归原作者 BOLD-Rainbow 所有, 如有侵权,请联系我们删除。