政安晨：【完全零基础】认知人工智能（三）【超级简单】的【机器学习神经网络】—— 三层神经网络示例

知识准备

咱们还没有演示过使用矩阵进行计算得到经由神经网络馈送的信号，我们也没有演示过多于2层的神经网络示例，在这篇文章里，咱们将构建一个三层神经网络的示例，并观察如何处理中间层的输出以作为最后第三层的输入，可以想象到这个示例估计会非常有趣。

如果小伙伴们第一次看到这篇文章，同时也对这类知识稍感陌生的话，可以先看看我这个系列的前两篇文章：
政安晨：【完全零基础】认知人工智能（一）【超级简单】的【机器学习神经网络】 —— 预测机https://blog.csdn.net/snowdenkeke/article/details/136139504政安晨：【完全零基础】认知人工智能（二）【超级简单】的【机器学习神经网络】—— 底层算法https://blog.csdn.net/snowdenkeke/article/details/136141888

现在开始

下图显示了具有3层、每层具有3个节点的神经网络示例（仅示例，没有标上所有的权重）：

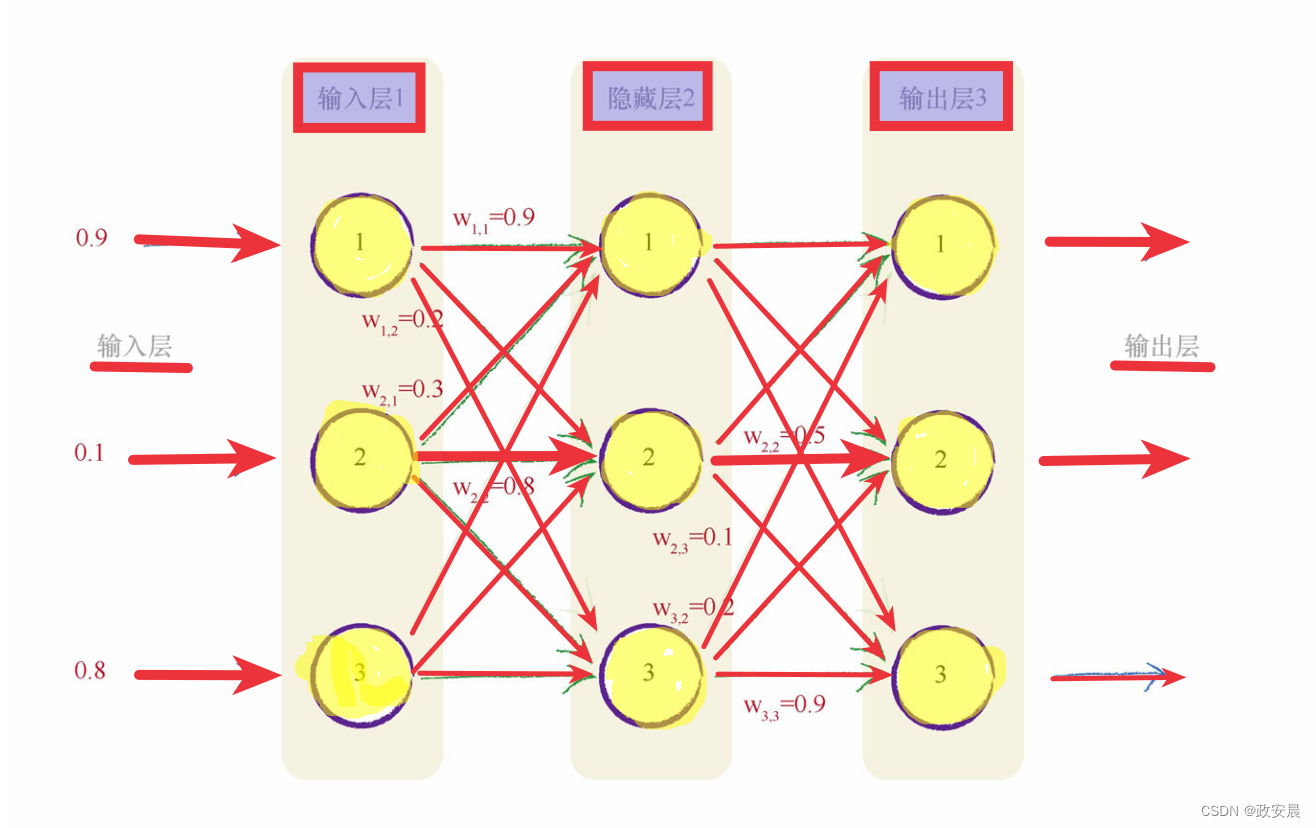
这里，咱们要介绍一点常用的术语。

正如我们所知道的：第一层为输入层，最后一层为输出层，中间层我们称之为隐藏层。

虽然隐藏层听起来很神秘、很黑暗，但是很遗憾，我们这样称呼中间层，其理由并不神秘：中间层的输出不需要很明显地表示为输出，因此我们称之为“隐藏”层。

目前咱们暂时没有对这个名称更好的解释了。

权重矩阵

好，咱们继续解析上图的这个神经网络：

我们观察到了3个输入是0.9、0.1和0.8。

所以，输入矩阵I为：

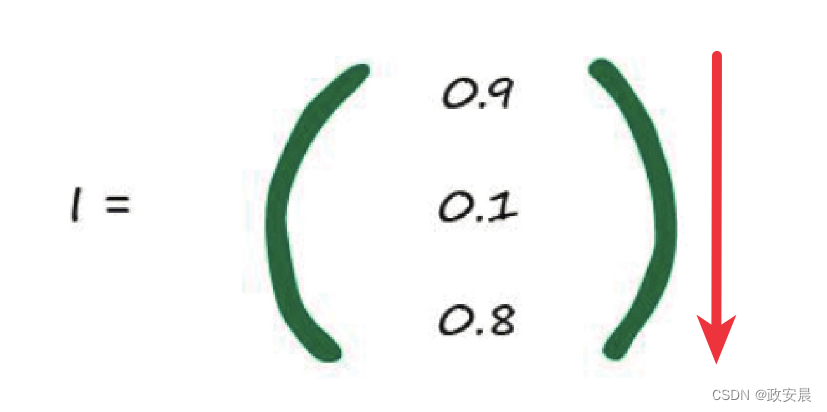
A

这是输入层所做的所有事情，就是表示输入，这样咱们已经完成了第一层输入层。

B

接下来是中间的隐藏层：

在这里，我们需要计算出输入到中间层每个节点的组合（调节）信号。

请记住，中间隐藏层的每个节点都与输入层的每个节点相连，因此每个节点都得到输入信号的部分信息。我们不想再像先前那样做大量的计算，我们希望尝试这种矩阵的方法。

正如我们刚才看到的，输入到中间层的组合调节信号为X=W·I，其中I为输入信号矩阵，W为权重矩阵。

这个神经网络的I、W是什么样的呢？

咱们刚才图中显示了这个神经网络的一些权重，但是并没有显示所有的权重。

下图显示了所有的权重，同样，这些数字是随机列举的，在这个示例中，权重没有什么特殊的含义，咱们随机取了一些值，方便演示而已。

您已经可以看到，第一个输入节点和中间隐藏层第一个节点之间的权重为w1,1=0.9，正如上图中的神经网络所示。

同样，你可以看到输入的第二节点和隐藏层的第二节点之间的链接的权重为w2,2=0.8。

图中并没有显示输入层的第三个节点和隐藏层的第一个节点之间的链接，我们随机编了一个权重w3,1=0.4。

**W[input_hidden]**是输入层和隐藏层之间的权重。

(说明一下：我们只是为了书写方便，用[ ] 来表示图中的下标)

我们需要另一个权重矩阵来表示隐藏层和输出层之间的链接，这个矩阵我们称之为：**W[hidden_output]**。

下图显示的是第二个矩阵**W[hidden_output]**，如先前一样，矩阵中填写了权重。

举个例子，同样你可以看到，隐藏层第三个节点和输出层第三个节点之间链接的权重为w3,3=0.9。·

如此，咱们就已经得到了排列整齐的权重矩阵。

矩阵计算

让我们一起继续算出输入到隐藏层的组合调节输入值。

我们应该给这个输入值一个名称，考虑到这个组合输入是到中间层，而不是最终层，因此，我们将它称为**X[hidden]**。

X[hidden]=W[input_hidden] · I

此处我们不打算进行完整的矩阵点积运算，以后使用计算机进行费力的数字运算，这里先展示如下图：

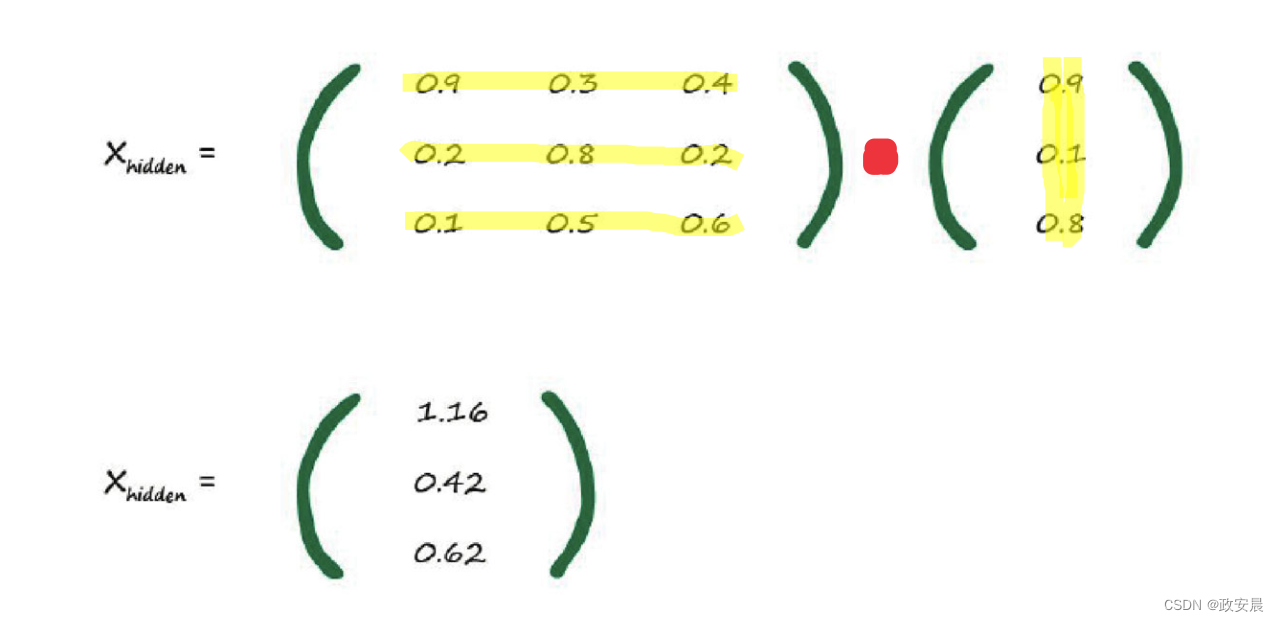
（说明：这个结果是咱们用计算机通过Python语言编程算出来的，这个以后说，咱这里先理解核心概念）

至此，咱们已经拥有了输入到中间隐藏层的组合调节输入值，它们为1.16、0.42和0.62。

咱们已经学会使用矩阵这个工具来完成这种复杂的工作，这是值得我们自豪的一个成就。

让我们可视化这些输入到第二层隐藏层的组合调节输入：

虽然到目前为止，一切都还顺利，但是，我们还有更多的工作要做。

我们对这些节点应用了S激活函数，使得节点对信号的反应更像自然界中节点的反应，你应该记得这一点吧！因此，现在，我们进行这个操作：

**O[hidden] **= sigmoid(X[hidden])

在X[hidden]层中的元素上应用S函数，生成中间隐藏层输出矩阵。

让我们检查第一个元素，确定一下过程：S函数为 ，因此，当x=1.16时， 是0.3135。这意味着y=1 /（1+0.3135）=0.761。你会看到，S函数的值域在0和1之间，所有的值都处在这个区间。(这一点很重要，小伙伴们要重视)

咱们现在梳理一下，当信号通过中间层时，我们对这些信号进行了计算，也就是说我们计算出了中间层的输出值，这个过程是非常清晰的，也就是应用激活函数到中间层的组合输入信号上，让我们使用这个新信息，更新下图：

如果这只是一个两层的神经网络，那么这些就是第二层的输出值，我们现在就可以停止计算了。

但是，由于还有第三层，我们不能在此处停止计算。

我们如何处理通过第三层的信号呢？

我们可以采用与处理第二层信号相同的方式进行处理，这没有任何实质的区别。

我们仍然可以得到第三层的输入信号，就像我们得到第二层的输入信号一样，我们依然使用激活函数，使得节点的反应与我们在自然界中所见到的一样。

因此，需要记住的事情是，不管有多少层神经网络，我们都“一视同仁”，即组合输入信号，应用链接权重调节这些输入信号，应用激活函数，生成这些层的输出信号。

我们不在乎是在计算第3层、第53层或是第103层的信号，使用的方法如出一辙。

咱们继续计算最终层的组合调节输入 X=W·I。

这一层的输入信号是第二层的输出信号，也就是我们刚刚解出的O[hidden]，所使用的权重就是第二层和第三层之间的链接权重**W[hidden_output]**，而不是第一层和第二层之间的链接权重。

因此，我们得到：

X[output]=W[hidden_output] · O[hidden]

因此，使用同样的方式计算出这个矩阵，这样我们得到了最后一层输出层的组合调节输出信号:

现在，更新示意图，看看咱们的进展，从初始输入信号开始，前馈信号，并得到了最终层的组合输入信号：

上述计算出来的输出信号还缺少了S函数，咱们继续：

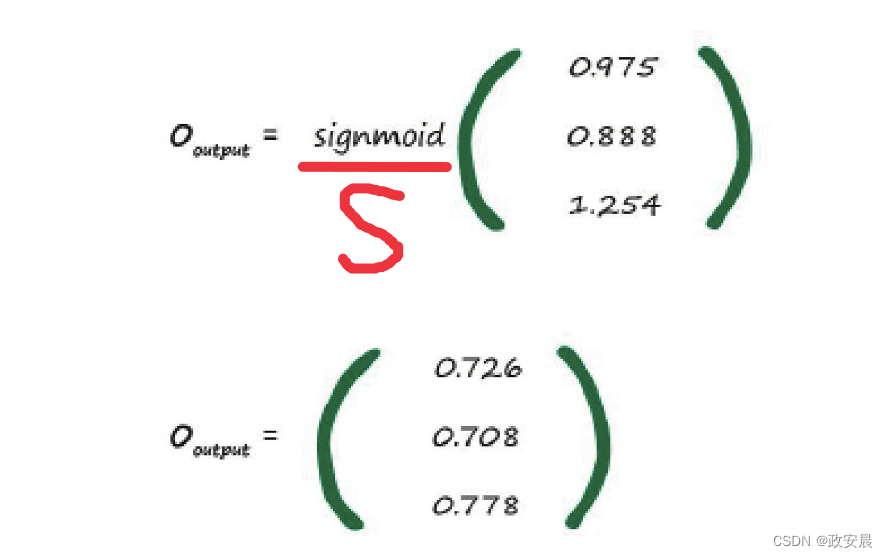
咱们就这样得到了神经网络的最终输出信号，咱们现在就将其显示在图上：

因此，这个三层示例神经网络的最终输出信号为0.726、0.708和0.778。

我们成功计算出了神经网络中的各个节点的信号，从信号进入神经网络，通过神经网络的各层，并得到了最终输出层的输出信号。

成果实现

接下来，将神经网络的输出值与训练样本中的输出值进行比较，计算出误差。

我们需要使用这个误差值来调整神经网络本身，进而改进神经网络的输出值：

现在，咱们将最终成果补充完整：

节点权重

咱们刚才已经说过，神经网络由多个节点组成，每个节点都有一个权重。

节点权重是神经网络中的参数，它们决定了节点对输入数据的响应程度。权重可以看作是节点的重要程度或者贡献度。节点的输入经过与权重相乘并加权求和后，再经过激活函数进行处理，得到节点的输出。

节点权重的初始值可以随机设定，然后通过训练神经网络来不断调整。

训练过程中，通过反向传播算法，计算出每个节点的梯度，并根据梯度的方向和大小来更新节点的权重。这样，经过多次迭代，神经网络可以不断调整节点权重，从而逐渐减小误差，并更好地拟合训练数据。

节点权重的调整是神经网络学习的关键步骤，它决定了神经网络的性能和准确度。

通过合理的选择和调整节点权重，神经网络可以对输入数据进行有效的分类、回归或其他任务。

我们使用误差值，也就是节点生成了答案与所知正确答案之间的差值，引导我们进行调整。

当输出和误差是多个节点共同作用的结果时，我们如何更新链接权重呢？

咱们现在将前面涉及到的神经网络中的节点拿出一个来放大，如下：

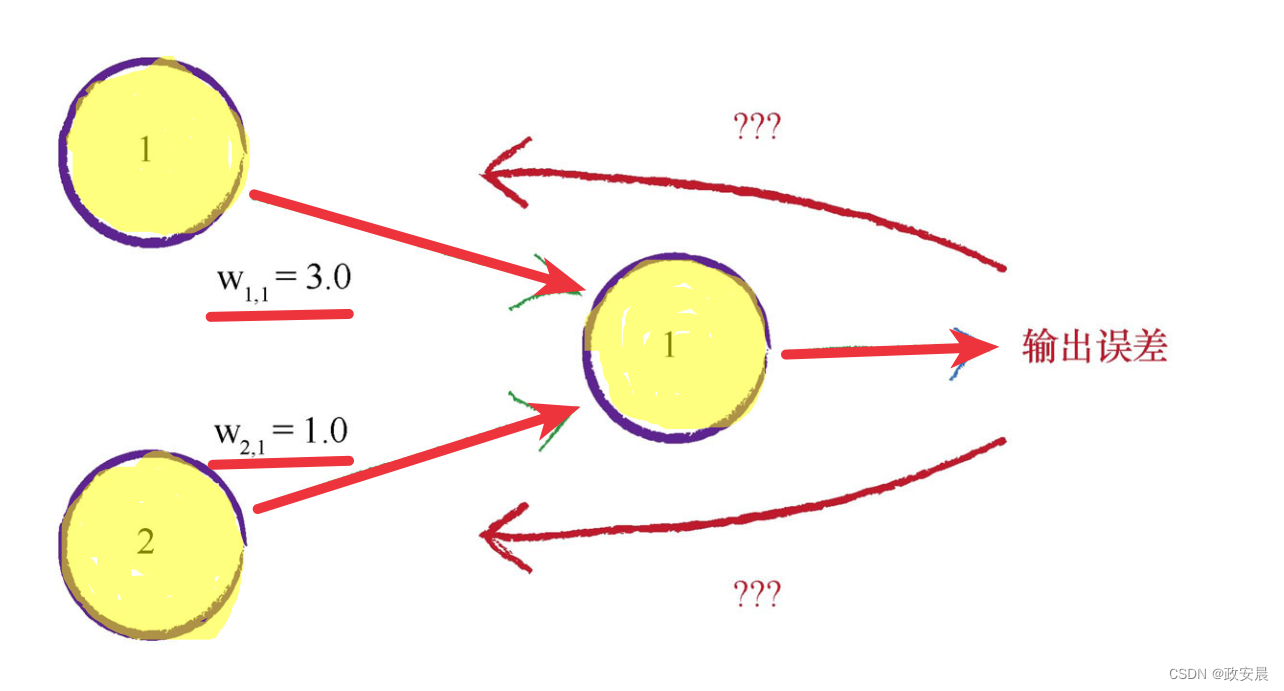
当只有一个节点前馈信号到输出节点，事情要简单得多，如果有两个节点，我们如何使用输出误差值呢？

使用所有的误差值，只对一个权重进行更新，这种做法忽略了其他链接及其权重，这样做毫无意义。

因为，多条链接都对这个误差值有影响。只有一条链接造成了误差，这种机会微乎其微。

如果我们改变了已经“正确”的权重而使情况变得更糟，那么在下一次迭代中，这个权重就会得到改进，因此神经网络并没有失去什么。这些方法是计算机科学经过多年积累，逐渐形成一种思想。

好了，咱们继续，先在所有造成误差的节点中平分误差，如下图所示：

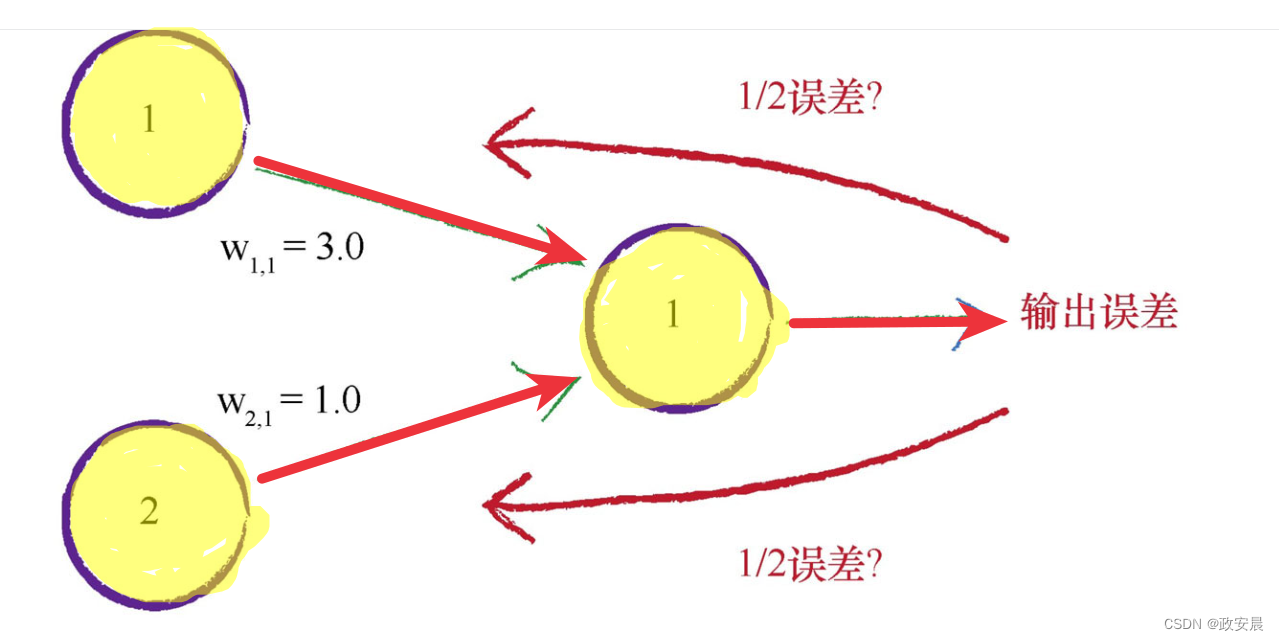
另一种思想是不等分误差。

与前一种思想相反，我们为较大链接权重的连接分配更多的误差。

为什么这样做呢？这是因为这些链接对造成误差的贡献较大。

下图详细阐释了这种思想：

此处，有两个节点对输出节点的信号做出了贡献，它们的链接权重分别是3.0和1.0。

如果按权重比例分割误差，那么我们就可以观察到输出误差的3/4应该可以用于更新第一个较大的权重，误差的1/4可以用来更新较小的权重。

我们可以将同样的思想扩展到多个节点。

如果我们拥有100个节点链接到输出节点，那么我们要在这100条链接之间，按照每条链接对误差所做贡献的比例（由链接权重的大小表示），分割误差。

咱们在两件事情上使用了权重：

第一件事情，在神经网络中，我们使用权重，将信号从输入向前传播到输出层。此前，我们就是在大量地做这个工作。

第二件事情，我们使用权重，将误差从输出向后传播到网络中，我们称这种方法为反向传播，您应该经常听到这个说法吧，呵呵。

如果输出层有2个节点，那么，咱们对第二个输出节点也会做同样的事情，第二个输出节点也会有其误差，这个误差也可以通过相连的链接进行类似的分割。

咱们接下来再详细地看一看这个概念。

反向传播

接下来咱们还是用具有2个输入节点和2个输出节点的简单神经网络来讲解。

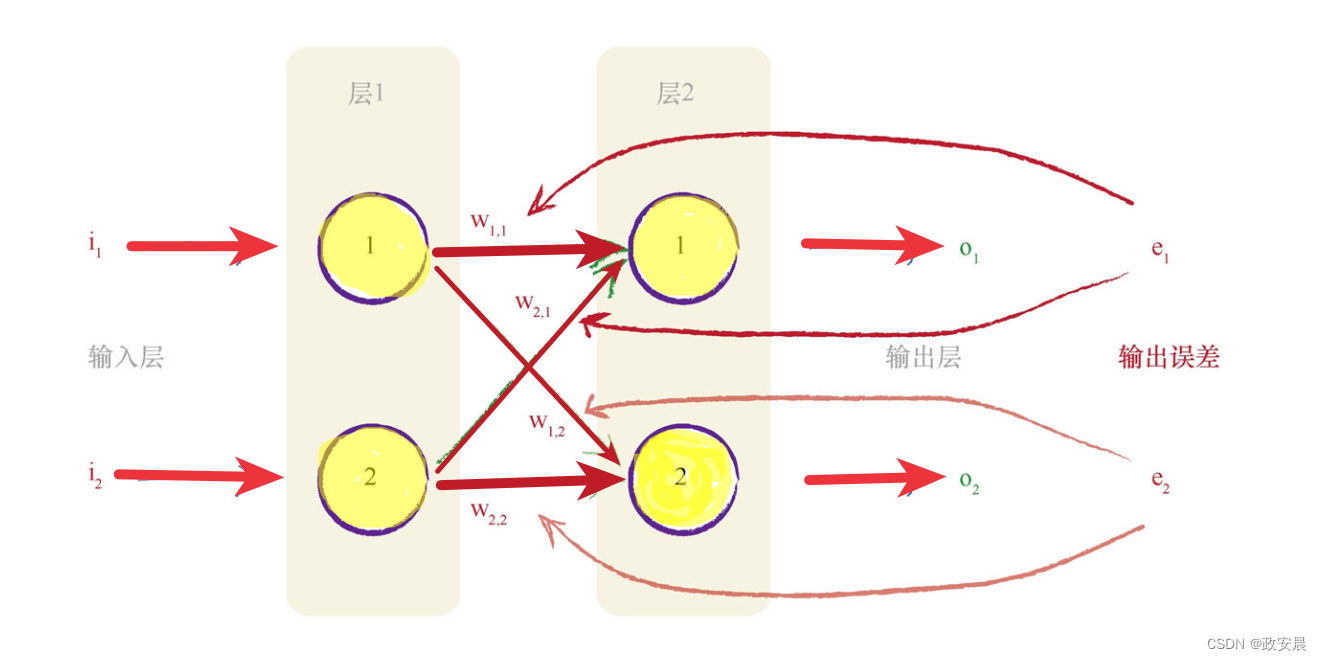
两个输出节点都有误差：事实上，在未受过训练的神经网络中，这是极有可能发生的情况。

咱们会发现，在神经网络中，咱们需要使用这两个误差值来告知如何调整内部链接权重。

我们可以使用与先前一样的方法，也就是跨越造成误差的多条链接，按照权重比例，分割输出节点的误差。

我们拥有多个节点这一事实并没有改变任何事情，对于第二个输出节点，我们只是简单地重复第一个节点所做的事情。

为什么如此简单呢？

这是由于进入输出节点的链接不依赖于到另一个输出节点的链接，因此事情就变得非常简单，在两组的链接之间也不存在依赖关系。

让我们再次观察上图：

我们将第一个输出节点的误差标记为e1。

（请记住，这个值等于由训练数据t1（当然t1并没与在图上标出来）提供的所期望的输出值与实际输出值o1之间的差，也就是，e1=(t1-o1)。）

我们将第二个输出节点的误差标记为e2。

从图咱们可以发现，按照所连接链接的比例，也就是权重w1,1和w2,1，我们对误差e1进行了分割。类似地，我们按照权重w1,2和w2,2的比例分割了e2。

让我们写出这些分割值：我们使用误差e1的信息，来调整权重w1,1和w2,1。

通过这种分割方式，我们使用e1的一部分来更新w1,1：

类似地，用来调整w2,1的e1部分为：

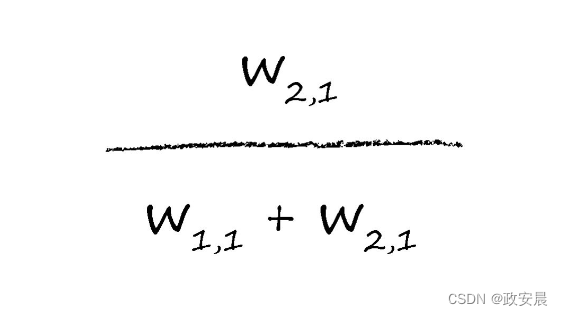
这些分数看起来可能令人有点费解，让我们详细阐释这些分数，在所有这些符号背后，思想非常简单，也就是误差e1要分割更大的值给较大的权重，分割较小的值给较小的权重。

如果w1,1是w2,1的2倍，比如说，w1,1=6, w2,1=3，那么用于更新w1,1的e1的部分就是6 /（6+3）=6/9=2/3。同时，这留下了1/3的e1给较小的权重w2,1，我们可以通过表达式3 /（6+3）=3/9确认这确实是1/3。

如果权重相等，就可以各分一半。让我们确定一下，假设w1,1=4和w2,1=4，那么针对这种情况，e1所分割的比例都等于4 /（4+4）=4/8=1/2。

咱们已经大概了解了这些概念，现在让咱们从一个更高的维度观察我们已经做的事情：

A. 我们知道需要使用误差来指导在网络内部如何调整一些参数，在这里也就是链接权重。

B. 我们明白了如何调整链接权重，并且我们使用链接权重来调节进入神经网络最终输出层的信号。在存在多个输出节点的情况下，我们也看到了这种调整过程没有变得复杂，只是对每个输出节点都进行相同的操作。

接下来我们要问的问题是，当神经网络多于2层时，会发生什么事情呢？在离最终输出层相对较远的层中，我们如何更新链接权重呢？

接下来咱们继续讲清楚。

反向传播误差到更多层中

下图展示了具有3层的简单神经网络，一个输入层、一个隐藏层和一个最终输出层。

从右手边的最终输出层开始，往回工作：

我们可以看到，我们使用在输出层的误差值引导调整馈送到最终层的链接权重。

更一般地，我们将输出误差标记为e[output]，将在输出层和隐藏层之间的链接权重标记为w[ho]。通过将误差值按权重的比例进行分割，我们计算出与每条链接相关的特定误差值。

通过可视化这种方法，咱们已经可以明白，对于额外的新层所需要做的事情。

简单说来，我们采用与隐藏层节点相关联的这些误差**e[hidden]，再次将这些误差按照输入层和隐藏层之间的链接权重w[ih]**进行分割。

下图就显示了此逻辑：

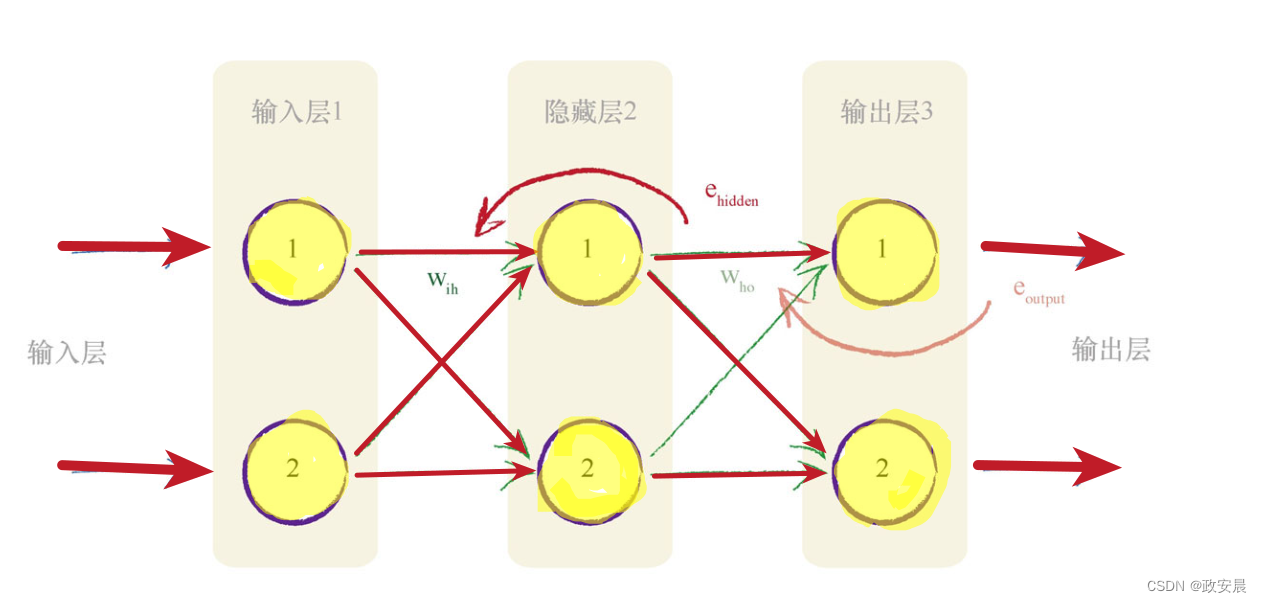
如果神经网络具有多个层，那么我们就从最终输出层往回工作，对每一层重复应用相同的思路。

误差信息流具有直观意义，您肯定已经明白称之为“误差的反向传播”的意义了。

如果对于输出层节点的e[output]，我们首先使用了输出误差，那么，对于隐藏层节点e[hidden]，我们使用什么误差呢？

中间隐藏层节点没有明确显示的误差，这是一个好问题：

咱们知道，向前馈送输入信号，隐藏层的每个节点确实有一个单一的输出。还记得，我们在该节点经过加权求和的信号上应用激活函数，才得到了这个输出。但是，我们如何才能计算出误差呢？

对于隐藏层的节点，我们没有目标值或所希望的输出值，我们只有最终输出层节点的目标值，这个目标值来自于训练样本数据。

让我们再次观察上图，寻找一些灵感！

隐藏层第一个节点具有两个链接，这两个链接将这个节点连接到两个输出层节点。

我们知道，沿着各个链接可以分割输出误差，就像我们先前所做的一样，这意味着，对于中间层节点的每个链接，我们得到了某种误差值，我们可以重组这两个链接的误差，形成这个节点的误差。实际上我们没有中间层节点的目标值，因此这种方法算得上退而求其次的最佳方法。

下图就可视化了这种想法：

虽然你可以相对清楚地观察到发生的事情，但是我们还是要再次演示，确认一下：我们需要隐藏层节点的误差，这样我们就可以使用这个误差更新前一层中的权重。我们称这个误差为**e[hidden]**。但是，我们不需要明确地回答这些误差是什么。我们的训练样本数据只给出了最终输出节点的目标值，因此不能说这个误差等于中间层节点所需目标输出值与实际输出值之间的差。

训练样本数据只告诉我们最终输出节点的输出应该为多少，而没有告诉我们任何其他层节点的输出应该是多少。这是这道谜题的核心。

咱们可以使用先前所看到的误差反向传播，为链接重组分割的误差。

因此，第一个隐藏层节点的误差是与这个节点前向连接所有链接中分割误差的和。

在上图中，我们得到了在权重为w1,1的链接上的输出误差**e[output,1]的一部分，同时也得到了在权重为w1,1的链接上第二个输出节点的输出误差e[output,2]**的一部分。

让咱们将这些值写下来：

这有助于我们看到这个理论的实际作用，下图详细阐释了在一个简单的具有实际数字的3层网络中，误差如何向后传播：

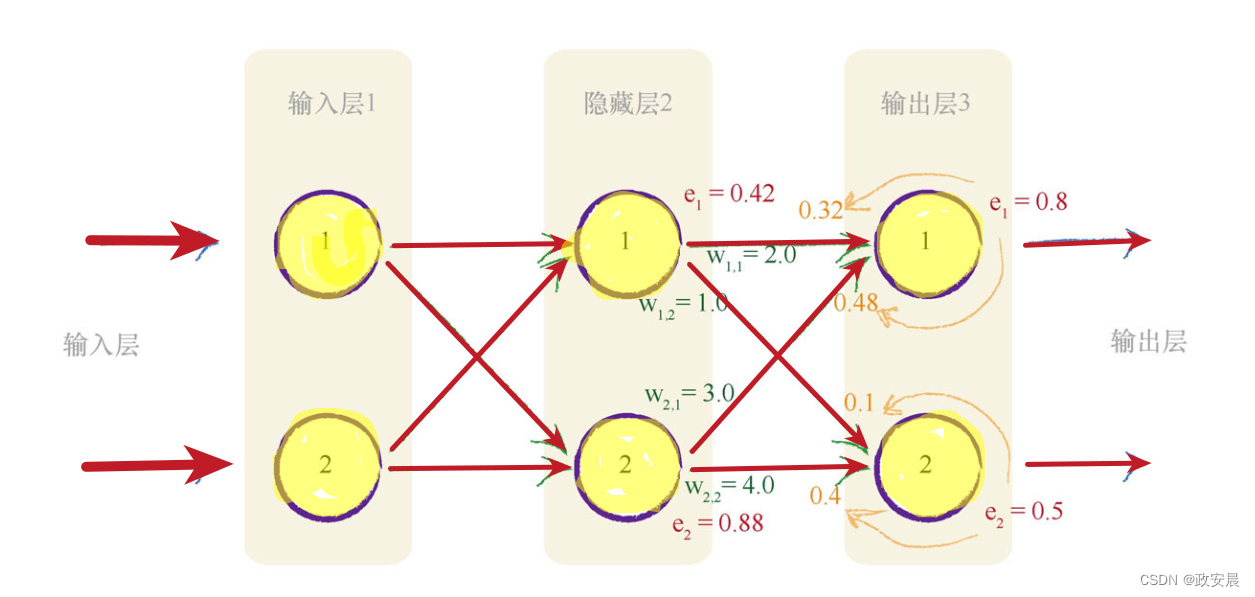
让我们演示一下反向传播的误差：

你可以观察到，第二个输出层节点的误差0.5，在具有权重1.0和4.0的两个链接之间，根据比例被分割成了0.1和0.4。

你也可以观察到，在隐藏层的第二个节点处的重组误差等于连接的分割误差之和，也就是0.48与0.4的和，等于0.88。

如下图所示（我们进一步向后工作，在前一层中应用相同的思路）：

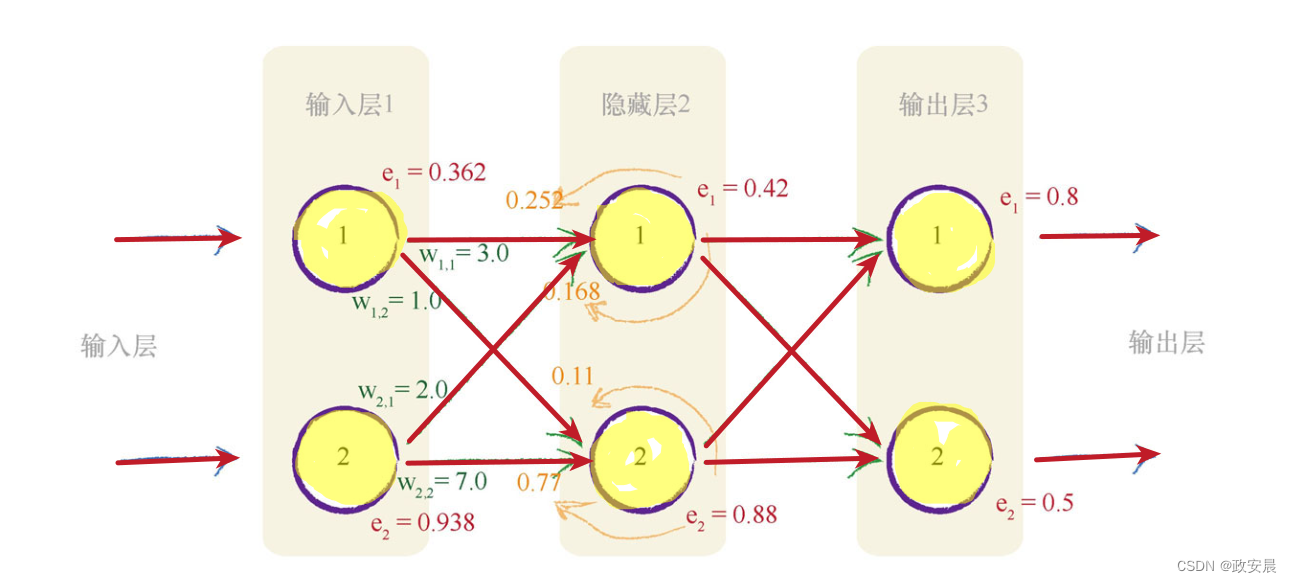
至此，咱们使用一个3层神经网络的示例演绎了的计算、权重与反向传播算法的原理。