线性回归:在实际中,对于情况较复杂的实际问题(因素不易化简,作用机理不详)可直接使用数据组建模,寻找简单的因果变量之间的数量关系, 从而对未知的情形作预报。这样组建的模型为拟合模型。
拟合模型的组建主要是处理好观测数据的误差,使用数学表达式从数量上近似因变量之间的关系拟合模型的组建是通过对有关变量的观测数据的观察、分析和选择恰当的数学表达防守得到的。
回归分析:回归分析就是用数理统计的方法,研究自然界中变量之间 存在的非确定的相互依赖和制约关系,并把这种非确定的相 互依赖和制约关系用数学表达式表达出来。其目的在于利用 这些数学表达式以及对这些表达式的精度估计,对未知变量 作出预测或检验其变化,为决策服务。 因此从某种程度而言,回归分析也可以认为是对自然界中 具有相关关系的变量进行简单的反演。
确定性关系和相关性关系
变量间的关系:确定行关系或函数关系 和不确定性关系
回归分析的流程
采集样本信息(x,y)——>(回归分析、散点图)回归方程——>回归方程的显著性——>对现实进行预测
回归模型
若两个变量x, y之间有线性相关关系,其回归模型为 y 称为因变量,x 称为自变量, 称为随机扰动,a, b 称为待估计的回归参数,下标 i 表示第 i 个观测值。
回归方程
去掉回归模型中的扰动项,得理论回归方程为 如果给出a 和b 的估计量分别为
则经验回归方程为:
一般的
残差
可视为扰动
的“估计量”。
离差平方和分解
因变量 y 的取值是不同的,y 取值的这种波动称为变差。变差来源于两个方面:
①、自变量 x 的取值不同造成的
②、 除 x 以外的其他因素(如x 对 y的非线性影响、测量误差等)的影响
对一个具体的观测值来说,变差的大小可以通过该实际观测值与其均值之差 来表示
总变差平方和 SST
回归平方和 SSR
残差平方和
总平方和(SST): 反映因变量的 n 个观察值与其均值的总离差
回归平方和(SSR) : 反映自变量 x 的变化对因变量 y 取值变化的影响,或者说,是由于 x 与 y 之间的线性关系引起的 y 的取值变化,也称为可解释的平方和
残差平方和(SSE) : 反映除 x 以外的其他因素对 y 取值的影响,也称为不可解释的平方和或剩余平方和
判定数据
定义: 回归平方和占总离差平方和的比例
判定系数的意义
反映回归直线的拟合程度
取值范围在 [ 0 , 1 ] 之间
——>1,说明回归方程拟合的越好;
——>0,说明回归方程拟合的越差
判定系数等于相关系数的平方,即=
线性回归函数regress
确定回归系数的值 : b = regress ( Y, X )
求回归系数的估计值和区间估计、并检验回归模型 [b, bint,r,rint,stats]=regress(Y,X,alpha)
b, bint——>回归系数的区间估计
r——>残差
rint ——>置信区间
stats——>用于检验回归模型的统计量, 有4个数值:判定系数、 F 值、与F 对应的概率p、误差方差的估计——>判定系数
越接近1,说明回归方程越显著
alpha——> 显著性水平(缺省时为0.05)
相关系数函数:corrcoef(x,y)
画残差图函数: rcoplot (r, rint )
残差正态检验 [h,p]=jbtes(r) 由jbtest检验,h=0表明残差服从正态分布,进而由Jarque–Bera检验可知h=0,p=1,故残差服从均值为零的正态分布;
进行一元线性回归的步骤:
1、做自变量与因变量的散点图,根据散点图的形状决定是否可以进行线性回归;
2、输入自变量与因变量;
3、利用命令: [b,bint,r,rint,stats]=regress(y,X,alpha),rcoplot(r,rint) 得到回归模型的系数以及异常点的情况
4、对回归模型进行检验 首先进行残差的正态性检验:jbtest,ttest
非线性回归
一元(多元)多项式回归 、非线性回归 、逐步回归
多项式回归
定义:研究一个因变量与一个或多个自变量间多项式的回归分析方法,称为多项式回归(Polynomial Regression)。如果自变量只有一个时,称为一元多项式回归;如果自变量有多个时,称为多元多项式回归
利用nlinfit函数作非线性回归 [beta, r] = nlinfit( X, y, fun, b0, options)
beta——>
r——>残差
y——>
b0——>回归系数初值
options——>优化属性设置
根据经验,人口增长的预测模型通常采用Logistic函数

renkou_data=[1975 0 92420 9.242 1976 1 93717 9.3717 1977 2 94974 9.4974 1978 3 96259 9.6259 1979 4 97542 9.7542 1980 5 98705 9.8705 1981 6 100072 10.0072 1982 7 101654 10.1654 1983 8 103008 10.3008 1984 9 104357 10.4357 1985 10 105851 10.5851 1986 11 107507 10.7507 1987 12 109300 10.93 1988 13 111026 11.1026 1989 14 112704 11.2704 1990 15 114333 11.4333 1991 16 115823 11.5823 1992 17 117171 11.7171 1993 18 118517 11.8517 1994 19 119850 11.985 1995 20 121121 12.1121 1996 21 122389 12.2389 1997 22 123626 12.3626 1998 23 124761 12.4761 1999 24 125786 12.5786 2000 25 126743 12.6743 2001 26 127627 12.7627 2002 27 128453 12.8453 2003 28 129227 12.9227 2004 29 129988 12.9988 2005 30 130756 13.0756];
year=renkou_data(:,1);
t=renkou_data(:,2);
y=renkou_data(:,4);
figure(1)
plot(year,y,'bo');
grid on;hold on;
xlabel('时间(1975-2005年)');
ylabel('中国人口(亿人)')
set(gca,'color','none')
fun=@(beta,t)[beta(1)./(1+beta(2)*exp(beta(3)*t))];
[beta,resid] = nlinfit(t,y,fun,[15,1,1]);
yp=fun(beta,t);
beta
plot(year,yp,'k-')
模型检验
ybar = mean(y);
SSE = sum((yp-ybar).^2);
SST= sum((y-ybar).^2);
r2 = SSE/SST
指数函数
基本形式: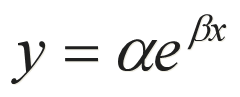
线性化方法 两端取对数得:lny = lna+ βx 令:y' = lny,则有y' = lna + β x
clc;clear all x=[1949 1954 1959 1964 1969 1974 1979 1984 1989 1994]; y=[5.4 6.0 6.7 7.0 8.1 9.1 9.8 10.3 11.3 11.8 ];
Y = log(y)'
X = [ones(length(x),1),x']
[b,bint,r,rint,stats] = regress(Y,X)
y_pred = exp(b(1))*exp(b(2)*x)
plot(x,y,'bo')
hold on
plot(x,y_pred,'r-')
legend('原始数据','回归曲线'
负指数函数
基本形式: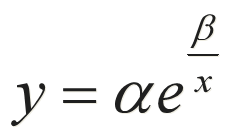
线性化方法 两端取对数得:lny = lna + β/ x 令:y' = lny, x' = 1/x,则有y' = lna + β x'
幂函数
基本形式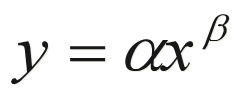
双曲线函数
基本形式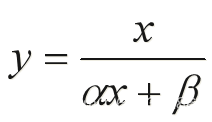
对数函数
基本形式: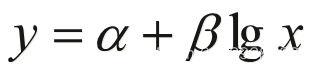
** S 型曲线**
基本形式: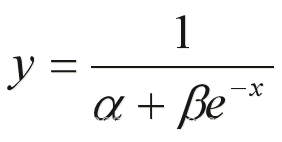
逐步回归stepwise
逐步回归简介
“最优”的回归方程就是包含所有对Y有影响的变量, 而不包含对Y影响不显著的变量回归方程。
选择“最优”的回归方程有以下几种方法:
从所有可能的因子(变量)组合的回归方程中选择 最优者
从包含全部变量的回归方程中逐次剔除不显著因子
从一个变量开始,把变量逐个引入方程;
“有进有出”的逐步回归分析
以第四种方法,即逐步回归分析法在筛选变量方面较为理想.
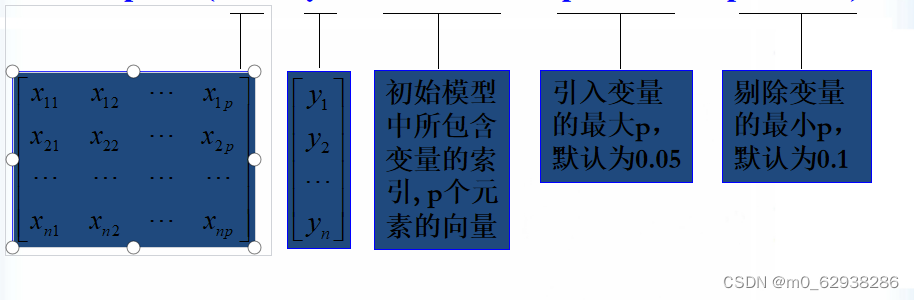
调用格式 :stepwise( X, y, inmodel, penter, premove)
版权归原作者 m0_62938286 所有, 如有侵权,请联系我们删除。