图像处理之高通滤波器与低通滤波器

高频与低频区分：

    在了解图像滤波器之前，先谈一下如何区分图像的高频信息和低频信息，所谓高频就是该像素点与周围像素差异较大，常见于一副图像的边缘细节和噪声等；而低频就是该像素点与周围像素差异变化不大，一般体现为图像的平坦区；

高通滤波器：

   高通滤波器指的是允许高于某一阈值的频率信息通过，过滤掉低于这一阈值的频率信息，从而大大衰减低频率的一种滤波器。在图像处理中，过滤频率信息采用的是傅里叶变换，把图像从空域转为频域进行处理。

1.傅里叶变换：

傅里叶变换公式：

               ![](https://img-blog.csdnimg.cn/01926ffe4ddf47f380476673c153595c.png)

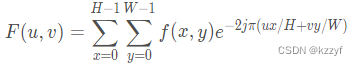
   图像高H，宽W。F(u,v)表示频域图像，f(x,y)表示时域图像。u的范围为[0,H−1]，v的范围为[0,W−1]。从这个公式中可以看出频率图像某一点值和整幅图像的灰度值都有关，而且计算量非常大，之前用opencv写过这个公式的傅里叶变换，一张很小的图片就要跑很长很长时间，所以一般不会采用这种方式，而是采用快速傅里叶变换，将减少运行时间，使得这种傅里叶变化可以运用在计算机的各个方面。

   运用这个公式之后，得到的频谱图，低频在四周，高频在中心，需要居中处理得到如下频谱，中心是低频，四周是高频：

    如果直接使用opencv定义的傅里叶函数，其是直接完成过居中处理的。

    高通滤波器过滤低频信息，就是将频域上的低频信息赋值，然后再采用逆变换将频域变换为空域。这里就有多种方法，滤波模板也可以自定义，这里就举例较简单的一种，将如下图像与频谱卷积相乘，黑色为像素为0，白色为1,再进行逆变换得到高通滤波器后的图像。

   逆变换后的图像，一般如下这样，图像：

   从这个结果图像可以知道，高通滤波器将低频信息过滤后就只有高频信息，高频一般是图像的边缘和噪点等。高通滤波器就是调整滤波模板，不同的滤波模板过滤的频率是不一样的，高通一般是过滤中心低频信息。知道高通滤波的过程后，低通滤波器就会很简单了。

低通滤波器：

    低通滤波器是和高通滤波器正好相反，低通滤波器是允许低频信息通过，滤掉高频信息，造成的结果就是图像变模糊了，一般用于去噪，因为噪点是高频信息。简单的说，就是靠近频谱图中心的低频部分给保留，远离频谱图中心的高频部分给去除掉。但是这会影响图像的清晰度。

    同理低通滤波器给一个滤波模板，将频谱中心保留，四周去掉，得到的低通滤波器后图像为如下：

     ![](https://img-blog.csdnimg.cn/0a6ca1f3fe31463db03c7ea933ce377d.png)

  可以看出图像变模糊了，根据给出的频率滤波模板的不同模糊程度也会不一样。

总结：

   以上都是基于频率滤波，根据傅里叶变换后的频谱进行滤波，再逆变换达到滤除不同频率得到目标图像。关于高通滤波和低通滤波，除了频率滤波，也可以采取空间滤波等，如常见的均值滤波和高斯滤波也可以去除高频信息达到平滑边缘的目的；拉普拉斯算子和梯度、Sobel等可以从空间上滤除低频信息得到边缘信息，可以利用其锐化边缘等。