实验一 k-means聚类建模
**1.****案例简介 **
某个餐饮公司因前期经验不善的影响而生意惨淡,现有位“接盘侠”接受了此餐厅。他为了扭转此现状,通过“充值 200 送 20 元”、“充值 500 元送 50 元”等优惠方式办理了几百张就餐充值卡,若干个月后收集了 500 名顾客的“最近一次消费时间间隔”(R)、“消费频率”(F)、“消费总额”(M)三类消费行为数据。此 “接盘侠”试图利用此数据将客户进行分类成不同客户群,并评价这些客户群的价值,进行实行做到针对性服务。然而此“接盘侠”不懂得对这些数据进行分析,你可以帮助他吗?(数据集为 consumption_data.xls)
** 消费者行为特征数据实例**
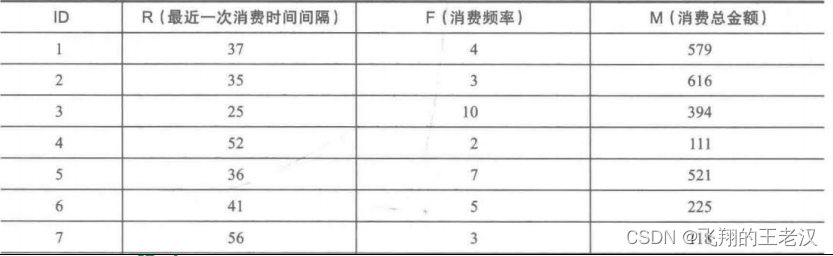
**2.****先验知识 **
2.1 因此餐饮店员工的失误导致收集的数据存在属性值缺失的情况
2.2 此数据中各属性的量纲(单位)不一致;
2.3 “接盘侠”凭借“砖家”的经验得知需要将客户划分为
**3 **个群体(簇),即优质客户、一般客户、低价值客户。
**3. ****数据分析步骤解读 **
3.1 数据预处理:去除缺省值(pandas. dropna(…)方法)
3.2 数 据 归 一 化 : 因 各 属 性 存 在 量 纲 ( 单 位 ) 不一致 (sklearn.preprocessing.sclae()等类似方法)
3.3 数据聚类:利用欧式距离和 k-means 聚类对客户进行分群,聚类结果如下图所示(
注意:因初始“类”中心和停止准则的不同每个人得****到结果不一样)
** 聚类结果**
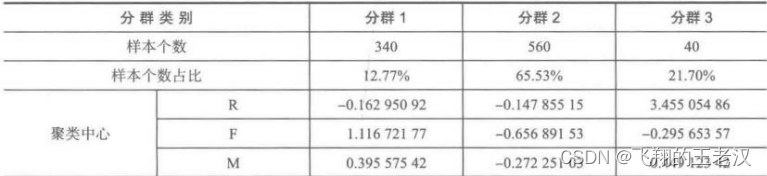
**3.4. ****密度函数绘制 **
为了对群体进行识别。针对每个群体的每个属性画出概率密度函数图像。(pandas.Series.plot(kind="kde")方法)
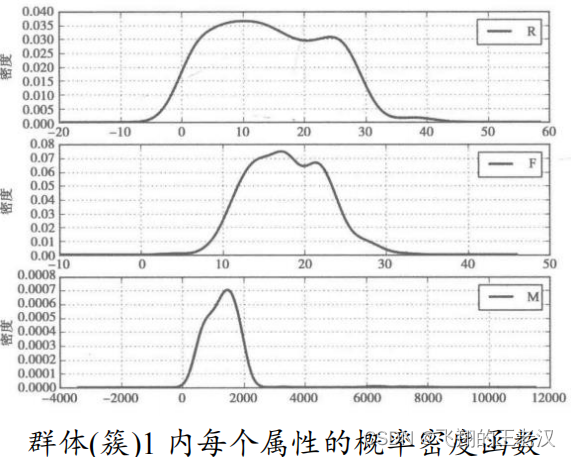
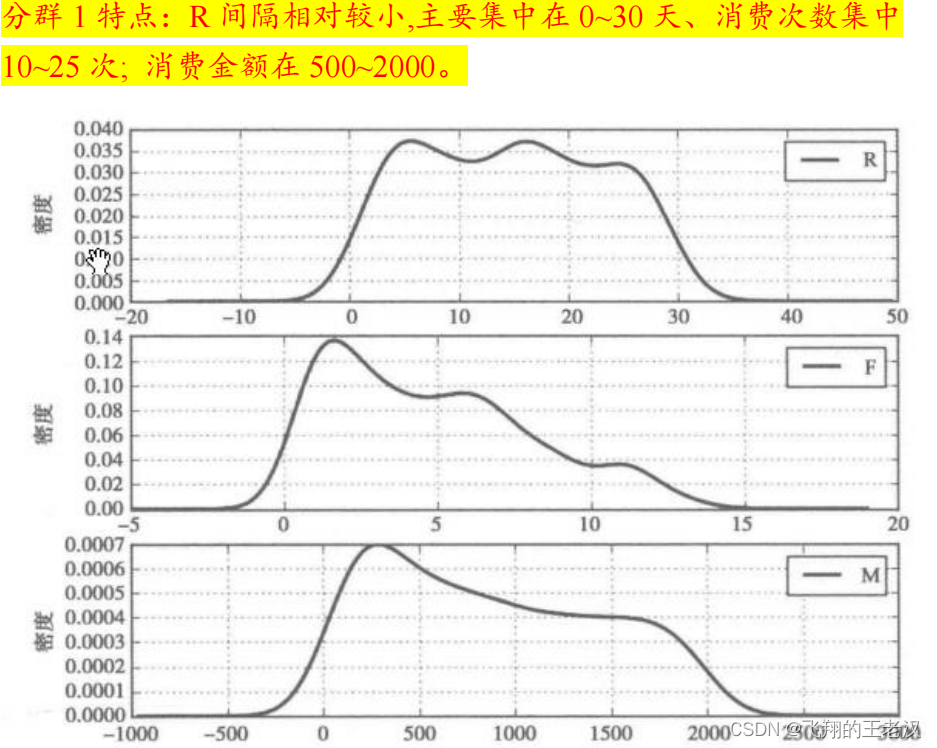
分群 2 特点:R 间隔分布在 0~30 天;消费次数集中在 0~12 次;消费金额在 0~1800。
分群 3 特点:R 间隔相对较大,间隔分布在 30~80 天;消费次数集中在0~15 次;消费金额在 0~2000。
对比分析**:****分群 ****1 时间间隔较短,消费次数多,而且消费金额较大,是消费、高价值人群。分群 *2 的时间间隔、消费次数和消费金额处于中等水平*,****代表着一般客户。分群 *3 的时间间隔较长,消费次数较少,消费金额也不是特别高*,****是价值较低的客户群体。 **
**4.****结论: **
“接盘侠”老板很高兴,他准备摩拳擦开始指定策略?什么策略呢?稳住高价值客服、。。。。。
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
k=3 #“接盘侠”凭借“砖家”的经验得知需要将客户划分为 3 个群体(簇),即优质客户、一般客户、低价值客户
data=pd.read_csv("C:/Users/wcj770801/Desktop/Python/consumption_data.csv",index_col=0)
data=data.dropna(axis=0,how='any') #数据预处理
data1=1.0*(data-data.mean())/data.std()
model=KMeans(3)
model.fit(data1)
print('label:\n',model.labels_)
print('cluster_centers_:\n',model.cluster_centers_)
r1=pd.Series(model.labels_).value_counts()
r2=pd.DataFrame(model.cluster_centers_)
r=pd.concat([r2,r1],axis=1) #数据归一化
r.columns=data.columns.tolist()+['类别数目']
print('r:\n',r) #数据聚类
output_data=pd.concat([data,pd.Series(model.labels_,index=data.index)],axis=1)
output_data.columns=list(data.columns)+['聚类类别']
def density_plot(data):
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
p=data.plot(kind='kde',linewidth=2,subplots=True,sharex=False) #密度函数绘制
plt.legend()
return plt
for i in range(k):
density_plot(data[output_data['聚类类别']==i]).show()
实验二 DBSCAN聚类算法
**1.****案例简介 **
利用随机模拟生成的二维数据点,观察 K-means 聚类算法与DBSCAN算法间的聚类区别,并观察在不同参数的条件下聚类效果。
**深刻理解 ****DBSCAN ****最大的难点在于确定 ****eps ****和 *min_samples 两个变量。*最后利用实际多个国家的自然数据,寻找特殊国家。 **
**2. ****不同聚类算法展示 **
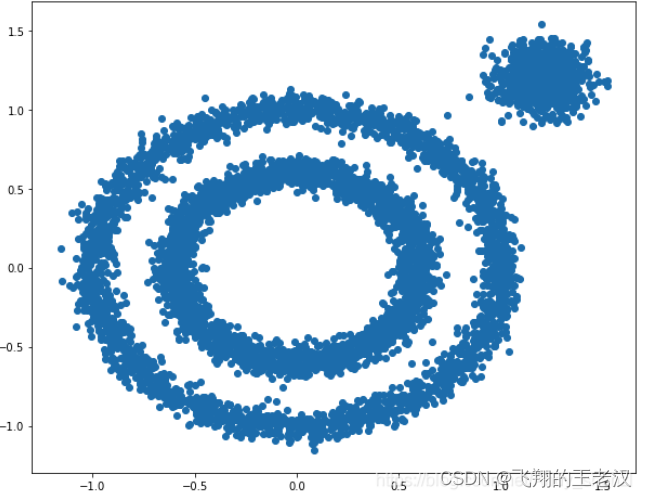
**2.1 ****原始数据生成 **
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X1, y1=datasets.make_circles(n_samples=5000, factor=.6,noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2,
centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9)
X = np.concatenate((X1, X2))
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
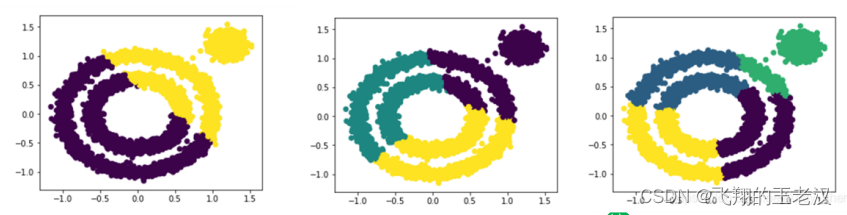
*2.2K-Means 聚类算法演示(k=2,3,4***) **
from sklearn.cluster import KMeans
for i in range(2,5):
y_pred = KMeans(n_clusters=i, random_state=9).fit_predict(X)
plt.figure(figsize=(5, 4))
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
**2.3 DBSCAN ****算法演示 **
**2.3.1 ****当 ****min_samples =10 ****不变,改变 ****eps **
from sklearn.cluster import DBSCAN
from sklearn import metrics
for i in range(0,20,5):
db=DBSCAN(eps = 0.1, min_samples = i).fit(X)
y_pred =DBSCAN(eps = 0.1, min_samples = i).fit_predict(X)
plt.figure(figsize=(3, 2))
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
print("eps=0.1,并且 min_samples=",i)
print("同质性: %0.3f" % metrics.homogeneity_score(labels_true,
db.labels_))
plt.show()
print("--"*2
**2.3.2 ****当 ****eps =0.1 ****不变,改变 **min_samples
**2.4 ****思考题 **
**如何选择最优的两个 ****eps ****和 ****min_samples ****取值呢? **
**3.****数据分析步骤解读 **
利用密度聚类对 12 个国家进行聚类,以寻找一些特殊国家。
**3.1 ****数据获取与预处理 **
读取数据集“country.txt”,并使用面积和人口这两个属性对以下 12 个国家进行密度聚类。
**注意**:需要数据进行归一化处理(属性值在 0~10000 之间)
**3.2 ****数据分析 **
调用 DBSCAN 算法,其中 eps=2000,min_samples=?(
**考虑一下 ****3****?**)
**3.3 ****数据展示 **
那一些国家比较特殊呢?横坐标面积,纵坐标人口
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
from sklearn import metrics
data = pd.read_csv('C:/Users/wcj770801/Desktop/Python/country.txt',sep='\t')
data1 = data[['面积km^2' , '人口']]
scaler = StandardScaler()
data2 = scaler.fit_transform(data1)
for i in range(3,5):
db = DBSCAN(eps = 200,min_samples = i).fit(data2)
y_pred = DBSCAN(eps = 0.1,min_samples = i).fit_predict(data2)
plt.figure(figsize=(3,2))
plt.scatter(data2[:,0],data2[:,1], c=y_pred)
print("eps=0.1,并且min_samples=",i)
# print("同质性:%0.3f" % metrics.homogeneity_score(labels_true,db.labels_))
plt.show()
print("--"*2)
实验三 聚类度量
**1.****案例简介 **
为探究我国城市在地理位置的相似程度,依据其地理位置(经纬度信息)将全国城市进行聚类分析,判定其自然风貌。
**2. ****数据分析步骤解读 **
**2.1 ****数据获取 **
读取 city.txt 数据集。
**考虑一下需要对数据的属性进行预处理吗? **
**2.2 ****聚类趋势探究 **
调用“hopkins_test”模块中的“hopkins_statistic”函数,探究城市经纬度数据是否存在类结构。
**2.3 ****确定聚类方法和距离度量 **
利用 K-means 聚类算法以及欧式距离度量。
**2.4 ****簇数确定 **
利用肘方法确定最优簇个数。在给定不同的聚类簇个数 k 值(k 可能取值为 2,3,4,5,7,8,9,10)的条件下,计算簇所有内离差和(对于聚类后的每个簇计算该簇内所有数据对象与其簇中心的距离的和,然后将 k个类簇各自的距离和相加得到一个函数
*var*(
*k*),
*k *就是类簇数)。其中横坐标聚类后簇的个数,纵坐标为在给定簇个数的条件下的所有簇内里差和。
平方和最大的时刻应该是分 1 个类——也就是不分类的时候,所有的向量到重心的距离都非常大,这样的距离的和是最大的。那么尝试着划分为 2 个类,3 个类,4 个类……随着分类的增多,第 k 次划分时,每个向量到自己簇的重心的距离会比上一次(k-1)次临近的机会更大,那么这个距离总和就会总体上缩小。极限情况就是最后被分成了 k 个类簇,n 整个空间向量的数量,也就是一个向量一个类簇,每个类簇一个成员。这种情况最后距离的和就变成了 0,因为每个向量距离自己(自己就是重心)的距离都是 0。
** ****2.5 ****聚类质量(轮廓系数) **
计算一下聚类后簇的个数分别为 5 和 6的条件下,轮廓系数的大小。 并选择最优的聚类方案。
from sklearn.neighbors import NearestNeighbors
from random import sample
from numpy.random import uniform
import numpy as np
from math import isnan
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt
def hopkins(X):
d = X.shape[1]
n = len(X)
m = int(0.1*n)
nbrs = NearestNeighbors(n_neighbors=1).fit(X.values)
rand_X = sample(range(0,n,1),m)
ujd = []
wjd = []
for j in range(0, m):
u_dist, _ = nbrs.kneighbors(uniform(np.amin(X, axis=0), np.amax(X, axis=0), d).reshape(1, -1), 2, return_distance=True)
ujd.append(u_dist[0][1])
w_dist, _ = nbrs.kneighbors(X.iloc[rand_X[j]].values.reshape(1, -1), 2, return_distance=True)
wjd.append(w_dist[0][1])
H = sum(ujd) / (sum(ujd) + sum(wjd))
if isnan(H):
print(ujd, wjd)
H = 0
return H
data = pd.read_csv('C:/Users/wcj770801/Desktop/Python/city.txt')
print("hopkins", hopkins(data))
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(data)
labels = kmeans_model.labels_
number = metrics.silhouette_score(data, labels, metric='euclidean')
print("轮廓系数:", number)
SSE = []
for i in range(1, 11): # k取1-10,计算簇内误差平方和
km = KMeans(n_clusters=i, random_state=2019)
km.fit(data)
SSE.append(km.inertia_)
plt.plot(range(1, 11), SSE, marker='v')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.xlabel('k值', size=15)
plt.ylabel('簇内误差平方和SSE', size=15)
# plt.scatter(data["longitude"],data["latitude"])
model_kmeans = KMeans(n_clusters=5, random_state=0)
model_kmeans.fit(data)
y_pre = model_kmeans.predict(data)
centers = model_kmeans.cluster_centers_
print(centers)
colors = ['r', 'c', 'b', 'y', 'g']
plt.figure()
for j in range(5):
index_set = np.where(y_pre == j)
cluster = data.iloc[index_set]
plt.scatter(cluster.iloc[:, 0], cluster.iloc[:, 1], c=colors[j], marker='.')
plt.plot(centers[j][0], centers[j][1], 'o', markerfacecolor=colors[j], markeredgecolor='k', markersize=8) # 画类别中心
plt.show()
版权归原作者 飞翔的王老汉 所有, 如有侵权,请联系我们删除。