环境混合物总体效应：加权分位数和回归（WQS）

1 WQS原理

加权分位数和(Weighted Quantile Sum, WQS)回归是一种在环境暴露中常见的高维数据集的多元回归的统计模型。该模型允许通过有监督的方式构建一个加权指数，以评估环境暴露的总体效应以及混合物中每一个成分对总体效应的贡献。

首先若某一类环境混合物中共有i个component，将每个component的值按分位数编码，如1st，2nd，3rd， 4th 分位数分别编为qi = 1，2，3，4。

WQS的拟合的模型如下：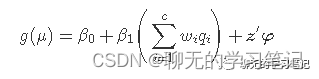

其中wi是环境混合物中每一个成分的权重，β1是加权分位数和指数（WQS指数）的回归系数，也就是环境混合物的总体效应。

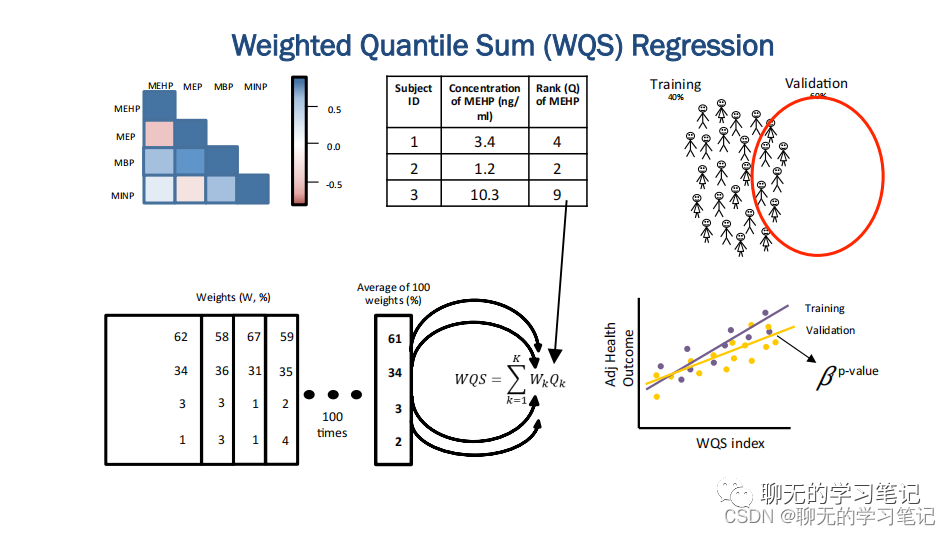
如图中所示流程，为了估计各成分的权重，构建WQS指数，WQS算法首先将数据集分为训练集和验证集，训练集用于权重的估计，验证集用于测试最终 WQS 指数的显着性。为了提高模型的稳定性，在训练集里进行B次自助抽样（B=100或1000）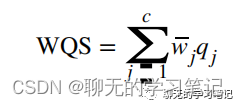

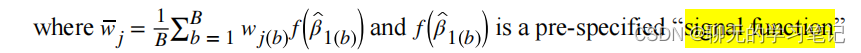
最后取100次自主抽样得到的权重的均值，或者只取100此中β1显著的那些次的权重均值作为最终得到的权重，然后在验证集中拟合模型（当样本量足够大时），若样本量小，也可在全部数据集中检验β1的显著性：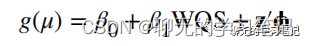

WQS的假设是：在混合物中每个暴露的效应都是同方向的（全为正或全为负），本质上是单向的，因为它只测试与给定结果正相关或负相关的混合效应。因此，在实践中，分析应该运行两次以测试正负两方向的关联。

2 WQS R语言示例

R语言的“gWQS”包可以实现WQS, 使用包里自带的示例数据wqs_data

install.packages("gWQS")
library(gWQS)
data(wqs_data)
toxic_chems <- names(wqs_data)[1:34]# we run the model and save the results in the variable "results"
results <- gwqs(y ~ wqs, mix_name = toxic_chems,
                data = wqs_data, q =4, validation =0.6, b =100,
                b1_pos =TRUE, b1_constr =FALSE, family ="gaussian",
                seed =1, plots =TRUE, tables =TRUE)

该WQS模型检验了我们的因变量y和根据四分位数暴露浓度排序估计的WQS指数之间的关系(q=4)；toxic_chems是混合物中所有components的名字，b=100为bootstrap的次数；60%的样本作为验证集；因为WQS只提供了混合效应的单向评估，我们只估计β1为正的权重(b1_pos=TRUE)；我们可以通过将该参数设置为假(b1_pos=false)来检验负关联。当我们估计权重时，我们也可以选择将β1约束为正(b1_pos=TRUE和b1_constr=TRUE)或负(b1_pos=false和b1_constr=TRUE)；seed为种子点

之后我们对权重进行排序并绘制权重的条形图：

w_ord <- order(results$final_weights$mean_weight)
mean_weight <- results$final_weights$mean_weight[w_ord]
mix_name <- factor(results$final_weights$mix_name[w_ord],
                      levels = results$final_weights$mix_name[w_ord])
data_plot <- data.frame(mean_weight, mix_name)
ggplot(data_plot, aes(x = mix_name, y = mean_weight, fill = mix_name))+
  geom_bar(stat ="identity", color ="black")+ theme_bw()+
  theme(axis.ticks = element_blank(),
           axis.title = element_blank(),
          axis.text.x = element_text(color='black'),
          legend.position ="none")+ coord_flip()

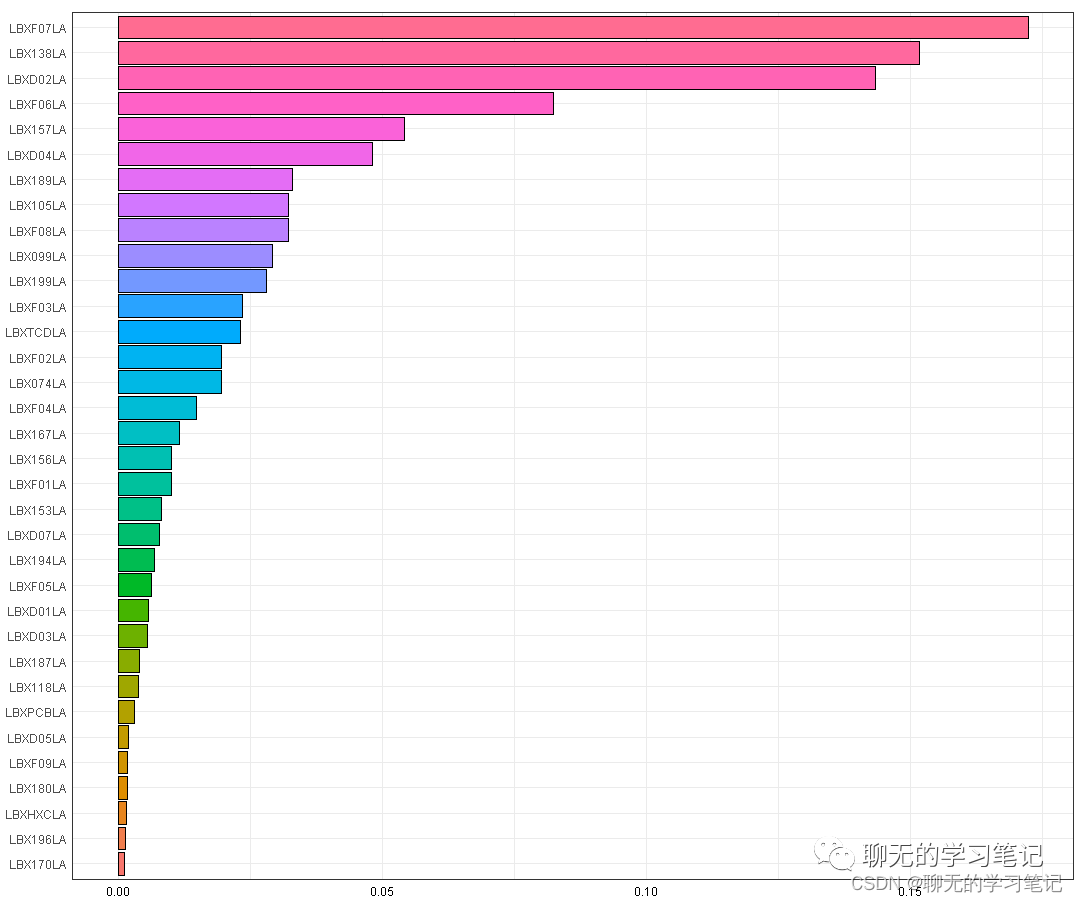
以及y和wqs指数的散点图加拟合线：

# scatter plot y vs wqs
 ggplot(results$y_wqs_df, aes(wqs, y_adj))+ geom_point()+
 stat_smooth(method ="loess", se =FALSE, size =1.5)+ theme_bw()

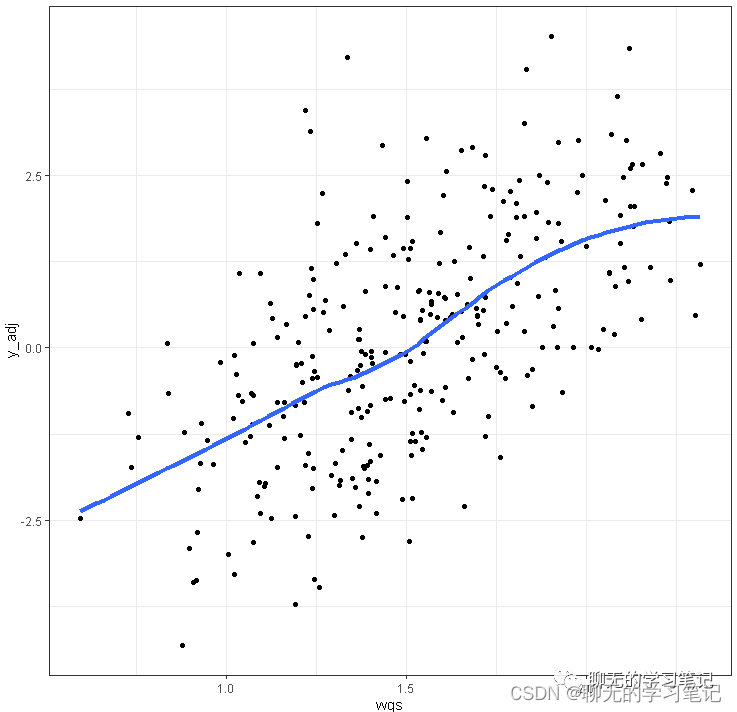
WQS 回归可以应用于多种类型的因变量，可以用逻辑回归、多项式、泊松和负二项式回归。WQS 的一个限制是由于必须将数据集拆分为训练集和验证集而导致的统计能力降低， 这种划分也可能导致不具代表性的数据集和不稳定的参数估计。

最后值得一提的是WQS的扩展方法：Bayesian WQS (Colicino et al. (2020))，它允许放宽单向假设，以及lagged WQS (Gennings et al. (2020))，它处理随时间变化的暴露混合物。

参考：

https://www.healthandenvironment.org/assets/images/Gennigs_Presentation_5-20-19.pdf
Renzetti S, Gennings C, Curtin P C. gWQS: an R package for linear and generalized weighted quantile sum (WQS) regression[J]. J Stat Softw, 2019: 1-9.

欢迎关注公众号：聊无的学习笔记