深度学习相关概念：计算图与反向传播

深度学习相关概念：计算图与反向传播

  在深度学习分类问题中，反向传播是一个重要的环节，它决定着模型是否能被训练，反向传播相当于一个负反馈，当一件事做完之后，会寻找当前事件做的不好的问题，进行回传，当下次在做的时候，进行优化。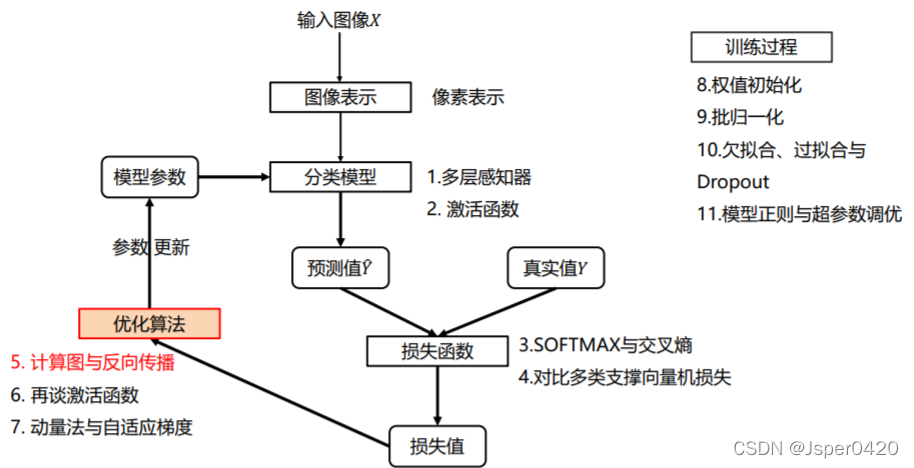

计算图

  在了解反向传播之前，我们必须首先明白什么是计算图，当只有构成计算图时，数据才能通过反向传播进行更新。
  计算图是一种有向图，它用来表达输入、输出以及中间变量之间的计算关系，图中的每个节点对应着一种数学运算。
  例如函数f=(x+y)²的计算图如下所示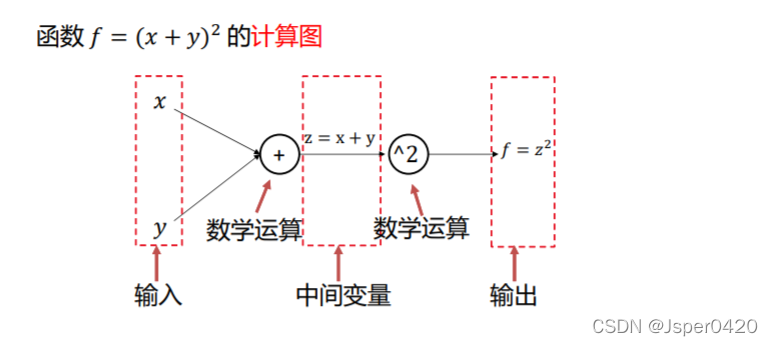

  这里假设x=1，y=2，则z=x+y=3，f=z²等于9，计算

         d
        
        
         f
        
       
       
        
         d
        
        
         z
        
       
      
      
       ∣
      
     
     
      
       z
      
      
       =
      
      
       3
      
     
    
    
     =
    
    
     2
    
    
     z
    
    
     =
    
    
     6
    
   
   
     \left. \frac{{\rm d}f}{{\rm d}z} \right| _{z=3}=2z=6 
   
  
 dzdf​∣∣∣∣​z=3​=2z=6

  又因为z对于x的导数

       d
      
      
       z
      
     
     
      
       d
      
      
       x
      
     
    
    
     =
    
    
     y
    
    
     =
    
    
     1
    
   
   
     \frac{{\rm d}z}{{\rm d}x}=y=1 
   
  
 dxdz​=y=1

  z对于y的导数

       d
      
      
       z
      
     
     
      
       d
      
      
       y
      
     
    
    
     =
    
    
     x
    
    
     =
    
    
     1
    
   
   
     \frac{{\rm d}z}{{\rm d}y}=x=1 
   
  
 dydz​=x=1

  根据链式法则即可求出

       d
      
      
       f
      
     
     
      
       d
      
      
       x
      
     
    
    
     =
    
    
     
      
       d
      
      
       f
      
     
     
      
       d
      
      
       z
      
     
    
    
     
      
       d
      
      
       z
      
     
     
      
       d
      
      
       x
      
     
    
    
     =
    
    
     6
    
   
   
     \frac{{\rm d}f}{{\rm d}x} =\frac{{\rm d}f}{{\rm d}z}\frac{{\rm d}z}{{\rm d}x}=6
   
  
 dxdf​=dzdf​dxdz​=6
 
  
   
    
     
      
       d
      
      
       f
      
     
     
      
       d
      
      
       y
      
     
    
    
     =
    
    
     
      
       d
      
      
       f
      
     
     
      
       d
      
      
       z
      
     
    
    
     
      
       d
      
      
       z
      
     
     
      
       d
      
      
       y
      
     
    
    
     =
    
    
     6
    
   
   
     \frac{{\rm d}f}{{\rm d}y}=\frac{{\rm d}f}{{\rm d}z}\frac{{\rm d}z}{{\rm d}y} =6
   
  
 dydf​=dzdf​dydz​=6

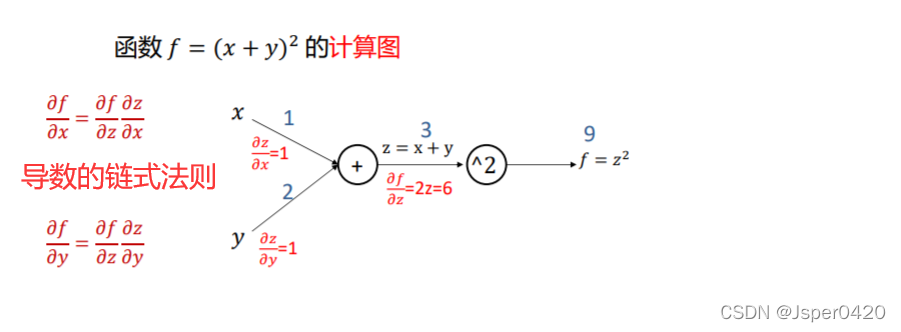
计算图总结

• 任意复杂的函数，都可以用计算图的形式表示
• 在整个计算图中，每个门单元都会得到一些输入，然后，进行下面两个计算：

  a) 这个门的输出值
  b) 其输出值关于输入值的局部梯度。

• 利用链式法则，门单元应该将回传的梯度乘以它对其的输入的局部梯度，从而得到整个网络的输出对该门单元的每个输入值的梯度（核心）。

反向传播

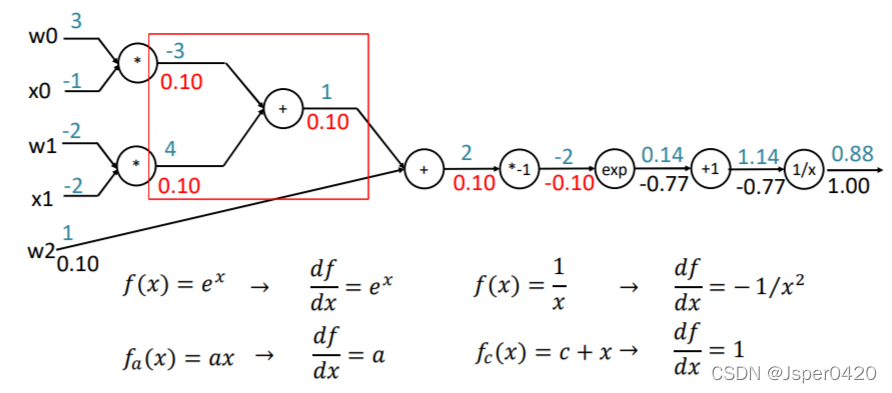
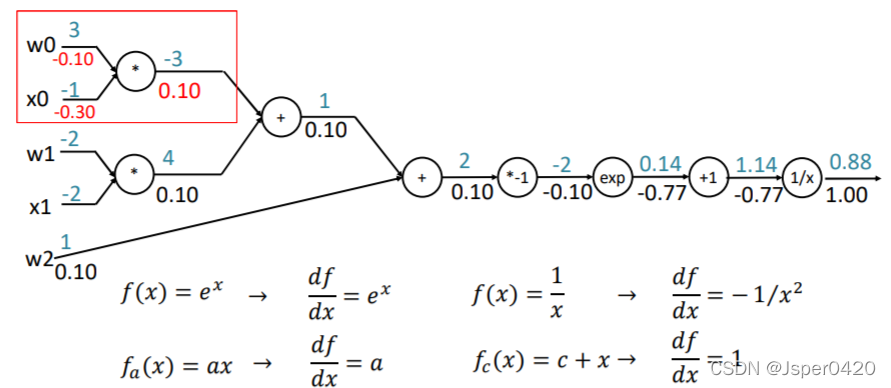
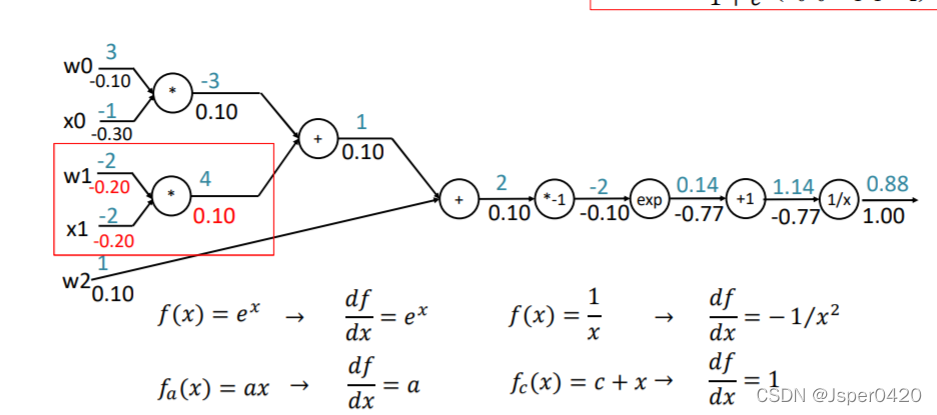
  根据上面总结，我们可以把反向传播应用到下面中，以函数f(w,x）为例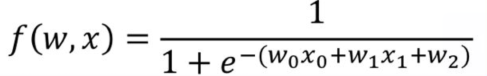
回传的梯度乘以它对其的输入的局部梯度，从而得到整个网络的输出对该门单元的每个输入值的梯度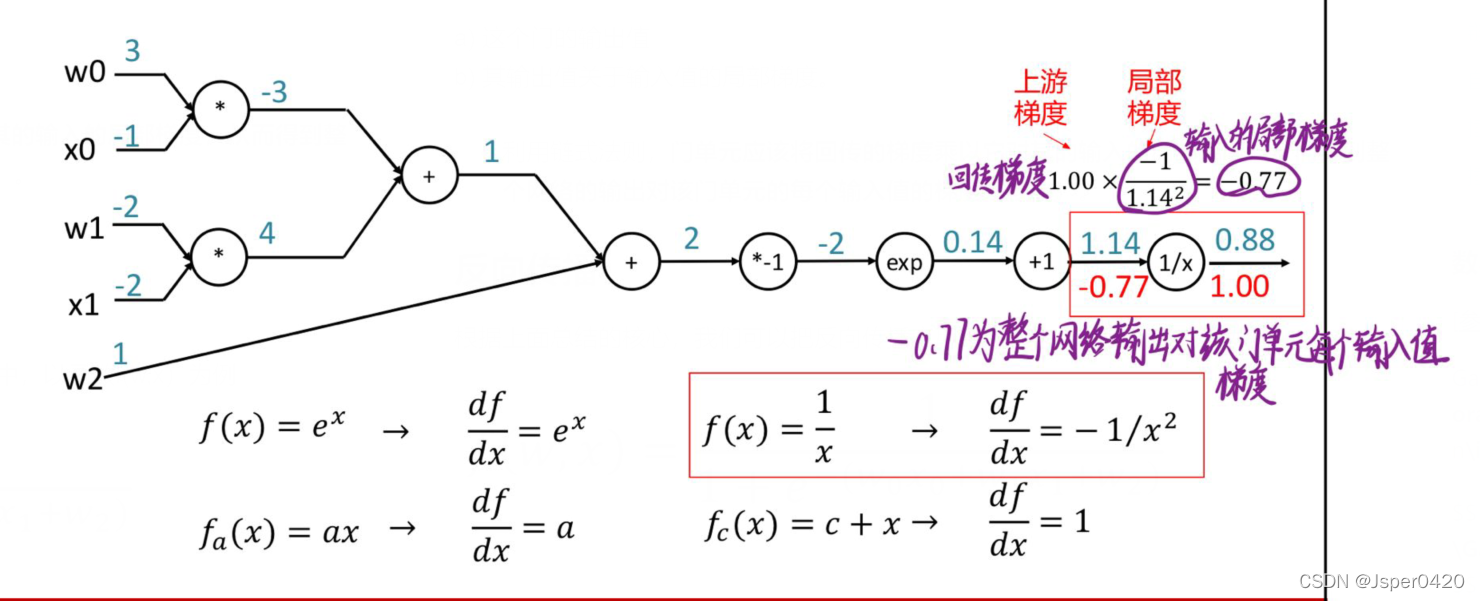
  以此类推可计算上一个门单元的输入梯度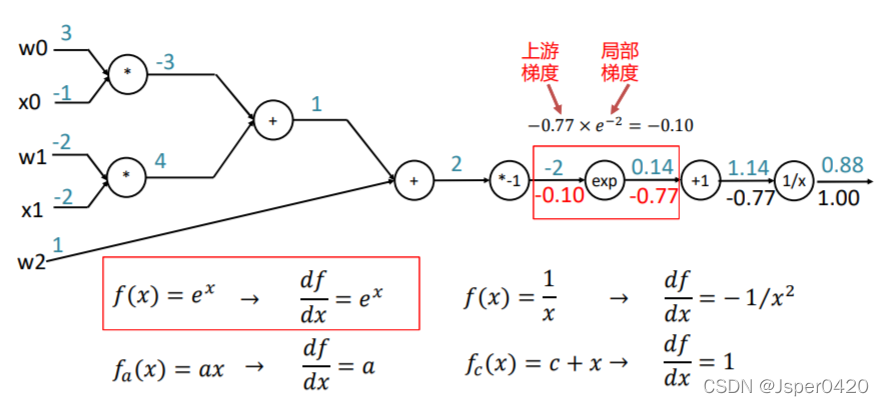

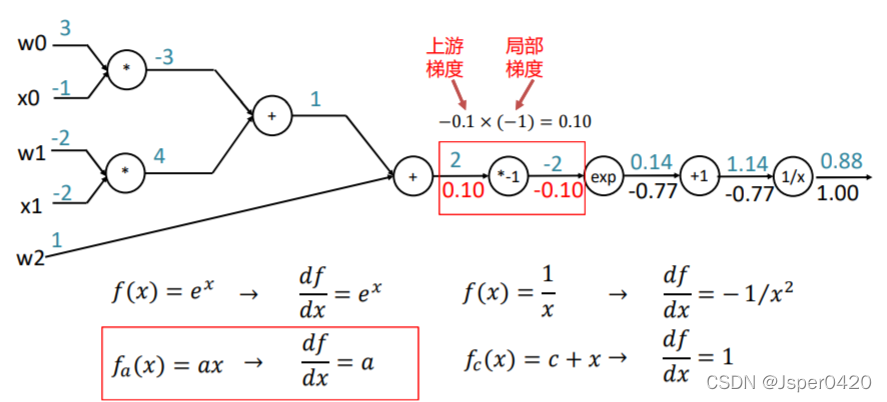
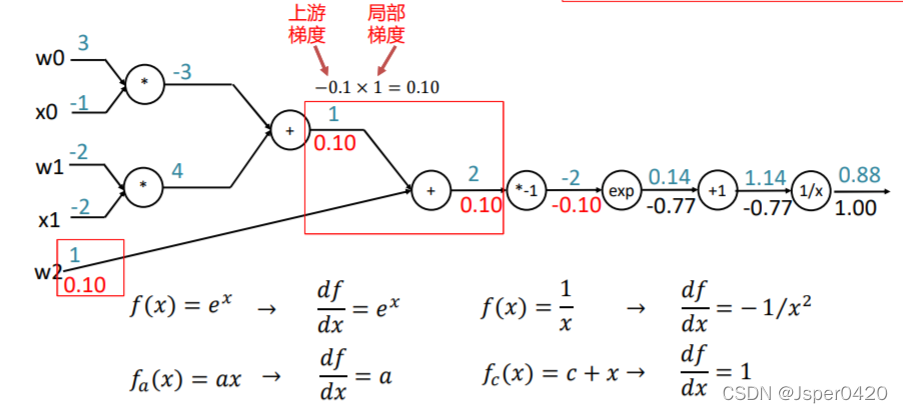
颗粒度

  在上述的反向传播中，每一次数据运算都要进行一次传播，显得有些冗余。我的前项计算结果在计算梯度的时候都是要用到的。如何避免这个现象了？这里讲了一个颗粒度问题，如果我把这个方框中的所有运算做写成一个函数，就写成一个这个Sigmoid的函数的话，写成一个函数，我直接把这个导数写出来的话，这个导数我可以直接相当于输入和输出就可以直接求出，那么我就可以直接求出这个0.1。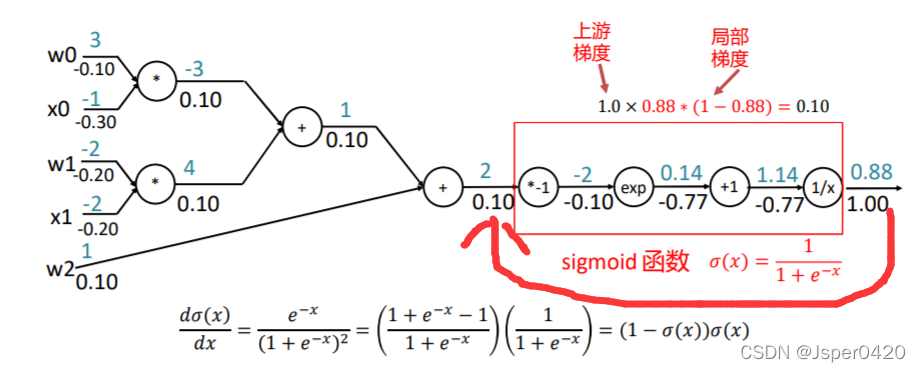
  这样求的好处是什么？在我的这个计算过程中，这点就不用分解成多处的分解成多次的这种局部门的计算，我可以直接用这一个公式就可以算到这个到这个点的梯度了，这样的好处就是计算效果快，所以在很多这个学习框架里面可以用的就是这样的，他的梯度可以推断是比较快的，你甚至把这整个写成一个函数，你一次就可以求出来w0、x0、w1、x1、w2所有的梯度。组合这种大函数，优势时速度快，计算少，但是缺点是你就得自己去写导函数。但是大部分情况是另一种情况，他把所有的算法都拆解成计算图，那么拆解的计算图了以后，那这样的话你不用自己求导函数，因为这种标准的分解流程它可以子在神经网络中写成标准的程序，它能帮你标准的完成这件事情。这就是计算图的颗粒度问题，计算块颗粒度小，计算慢；但颗粒度越大，你就要自己写求导函数，这就是计算图的颗粒度，它跟效率有关系。