
使用DBSCAN标识为员工分组

照片由Ishan @seefromthesky 在 Unsplash拍摄
**基于密度的噪声应用空间聚类(DBSCAN)**是一种无监督的ML聚类算法。无监督的意思是它不使用预先标记的目标来聚类数据点。聚类是指试图将相似的数据点分组到人工确定的组或簇中。它可以替代KMeans和层次聚类等流行的聚类算法。
在我们的示例中,我们将检查一个包含15,000名员工的人力资源数据集。数据集包含员工的工作特征,如工作满意度、绩效评分、工作量、任职年限、事故、升职次数。
KMeans vs DBSCAN
KMeans尤其容易受到异常值的影响。当算法遍历质心时,在达到稳定性和收敛性之前,离群值对质心的移动方式有显著的影响。此外,KMeans在集群大小和密度不同的情况下还存在数据精确聚类的问题。K-Means只能应用球形簇,如果数据不是球形的,它的准确性就会受到影响。最后,KMeans要求我们首先选择希望找到的集群的数量。下面是KMeans和DBSCAN如何聚类同一个数据集的示例。
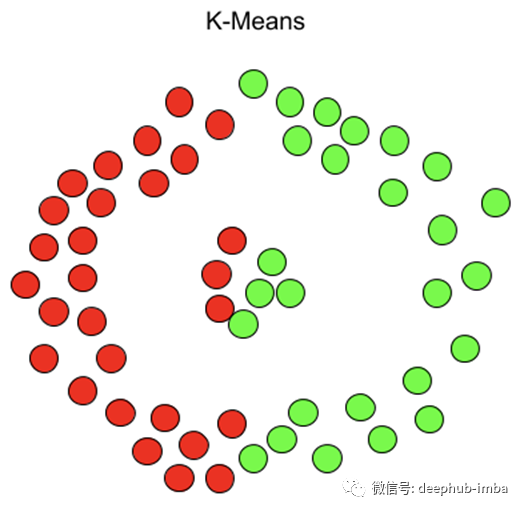
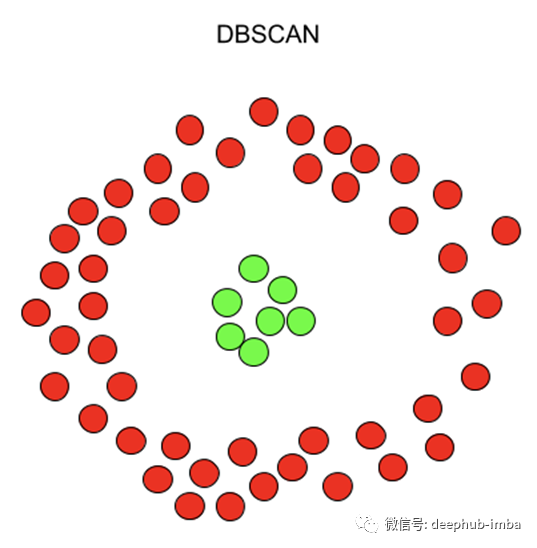
另一方面,DBSCAN不要求我们指定集群的数量,避免了异常值,并且在任意形状和大小的集群中工作得非常好。它没有质心,聚类簇是通过将相邻的点连接在一起的过程形成的。
DBSCAN是如何实现的呢?
首先,让我们定义Epsilon和最小点、应用DBSCAN算法时需要的两个参数以及一些额外的参数。
- Epsilon (ɛ):社区的最大半径。如果数据点的相互距离小于或等于指定的epsilon,那么它们将是同一类的。换句话说,它是DBSCAN用来确定两个点是否相似和属于同一类的距离。更大的epsilon将产生更大的簇(包含更多的数据点),更小的epsilon将构建更小的簇。一般来说,我们喜欢较小的值是因为我们只需要很小一部分的数据点在彼此之间的距离内。但是如果太小,您会将集群分割的越来越小。
- 最小点(minPts):在一个邻域的半径内minPts数的邻域被认为是一个簇。请记住,初始点包含在minPts中。一个较低的minPts帮助算法建立更多的集群与更多的噪声或离群值。较高的minPts将确保更健壮的集群,但如果集群太大,较小的集群将被合并到较大的集群中。
如果“最小点”= 4,则在彼此距离内的任意4个或4个以上的点都被认为是一个簇。
其他参数
**核心点:**核心数据点在其近邻距离内至少有的最小的数据点个数。
我一直认为DBSCAN需要一个名为“core_min”的第三个参数,它将确定一个邻域点簇被认为是聚类簇之前的最小核心点数量。
**边界点:**边界数据点位于郊区,就像它们属于近邻点一样。(比如w/在epsilon距离内的核心点),但需要小于minPts。
**离群点:**这些点不是近邻点,也不是边界点。这些点位于低密度地区。
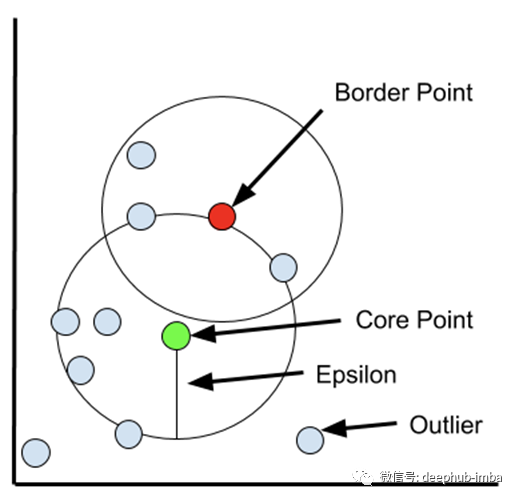
首先,选择一个在其半径内至少有minPts的随机点。然后对核心点的邻域内的每个点进行评估,以确定它是否在epsilon距离内有minPts (minPts包括点本身)。如果该点满足minPts标准,它将成为另一个核心点,集群将扩展。如果一个点不满足minPts标准,它成为边界点。随着过程的继续,算法开始发展成为核心点“a”是“b”的邻居,而“b”又是“c”的邻居,以此类推。当集群被边界点包围时,这个聚类簇已经搜索完全,因为在距离内没有更多的点。选择一个新的随机点,并重复该过程以识别下一个簇。
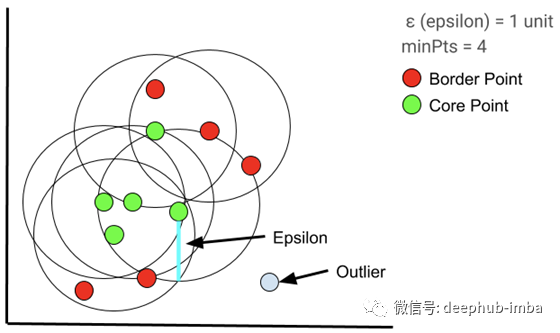
如何确定最优的Epsilon值
估计最优值的一种方法是使用k近邻算法。如果您还记得的话,这是一种有监督的ML聚类算法,它根据新数据点与其他“已知”数据点的距离来聚类。我们在带标记的训练数据上训练一个KNN模型,以确定哪些数据点属于哪个聚类。当我们将模型应用到新数据时,算法根据与训练过的聚类的距离来确定新数据点属于哪一个聚类。我们必须确定“k”参数,它指定在将新数据点分配给一个集群之前,模型将考虑多少个最邻近点。
为了确定最佳的epsilon值,我们计算每个点与其最近/最近邻居之间的平均距离。然后我们绘制一个k距离,并选择在图的“肘部”处的epsilon值。在y轴上,我们绘制平均距离,在x轴上绘制数据集中的所有数据点。
如果选取的epsilon太小,很大一部分数据将不会被聚类,而一个大的epsilon值将导致聚类簇被合并,大部分数据点将会在同一个簇中。一般来说,较小的值比较合适,并且作为一个经验法则,只有一小部分的点应该在这个距离内。
如何确定最佳minPts
通常,我们应该将minPts设置为大于或等于数据集的维数。也就是说,我们经常看到人们用特征的维度数乘以2来确定它们的minPts值。
就像用来确定最佳的epsilon值的“肘部方法”一样,minPts的这种确定方法并不是100%正确的。
DBSCAN聚类的评价方式
影像法:该技术测量集群之间的可分离性。首先,找出每个点与集群中所有其他点之间的平均距离。然后测量每个点和其他簇中的每个点之间的距离。我们将两个平均值相减,再除以更大的那个平均值。
我们最终想要的是一种较高(比如最接近1)的分数,表明存在较小的簇内平均距离(紧密簇)和较大的簇间平均距离(簇间分离良好)。
**集群可视化解释:**获得集群之后,解释每个集群非常重要。这通常是通过合并原始数据集和集群并可视化每个集群来完成的。每个集群越清晰越独特越好。我们将在下面实现这个过程。
DBSCAN的优点
- 不需要像KMeans那样预先确定集群的数量
- 对异常值不敏感
- 能将高密度数据分离成小集群
- 可以聚类非线性关系(聚类为任意形状)
DBSCAN的缺点
- 很难在不同密度的数据中识别集群
- 难以聚类高维数据
- 对极小点的参数非常敏感
让我们尝试一下
importnumpyasnp
importpandasaspd
importmatplotlib.pyplotasplt
importseabornassns
importplotly.offlineaspyo
pyo.init_notebook_mode()
importplotly.graph_objsasgo
fromplotlyimporttools
fromplotly.subplotsimportmake_subplots
importplotly.offlineaspy
importplotly.expressaspx
fromsklearn.clusterimportDBSCAN
fromsklearn.neighborsimportNearestNeighbors
fromsklearn.metricsimportsilhouette_score
fromsklearn.preprocessingimportStandardScaler
fromsklearn.decompositionimportPCAplt.style.use('fivethirtyeight')
fromwarningsimportfilterwarnings
filterwarnings('ignore')
withopen('HR_data.csv') asf:
df = pd.read_csv(f, usecols=['satisfaction_level', 'last_evaluation', 'number_project',
'average_montly_hours', 'time_spend_company', 'Work_accident',
'promotion_last_5years'])
f.close()

1. 标准化
由于数据集中的特特征不在相同的范围内,所以我们需要对整个数据集进行标准化。换句话说,我们数据集中的每个特征对于它们的数据都有独特的大小和范围。满意度水平增加一分并不等于最后评价增加一分,反之亦然。由于DBSCAN利用点之间的距离(欧几里得)来确定相似性,未缩放的数据会产生问题。如果某一特征在其数据中具有较高的可变性,则距离计算受该特征的影响较大。通过缩放特征,我们将所有特征对齐到均值为0,标准差为1。
scaler = StandardScaler()
scaler.fit(df)
X_scale = scaler.transform(df)df_scale = pd.DataFrame(X_scale, columns=df.columns)
df_scale.head()

2. 特征降维
在一些算法如KMeans中,如果数据集的特征维度太大,就很难精确地构建聚类。高维数并不一定意味着成百上千维度的特征。甚至10个维度的特征也会造成准确性问题。
特征降维背后的理论是将原始特征集转换为更少的人工派生特征,这些特征仍然保留了原始特征中包含的大部分信息。
最流行的特征降维技术之一是主成分分析(PCA)。PCA将原始数据集缩减为指定数量的特征,并将这些特征称为主成分。我们必须选择我们希望看到的主成分的数量。我们在我关于KMeans集群的文章中讨论了减少特性,我强烈建议您看一看(链接)。
首先,我们需要确定适当的主成分数量。3个主成分似乎占了大约75%的方差。
pca = PCA(n_components=7)
pca.fit(df_scale)
variance = pca.explained_variance_ratio_var=np.cumsum(np.round(variance, 3)*100)
plt.figure(figsize=(12,6))
plt.ylabel('% Variance Explained')
plt.xlabel('# of Features')
plt.title('PCA Analysis')
plt.ylim(0,100.5)plt.plot(var)
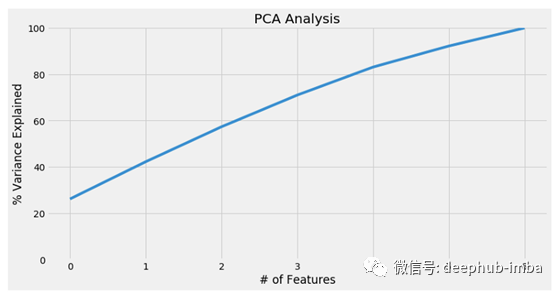
现在我们知道了维持一个特定百分比的方差所需的主成分的数量,让我们对原始数据集应用一个3成分的主成分分析。请注意,第一个主成分占到与原始数据集方差的26%。在本文的其余部分中,我们将使用“pca_df”数据框架。
pca = PCA(n_components=3)
pca.fit(df_scale)
pca_scale = pca.transform(df_scale)pca_df = pd.DataFrame(pca_scale, columns=['pc1', 'pc2', 'pc3'])
print(pca.explained_variance_ratio_)
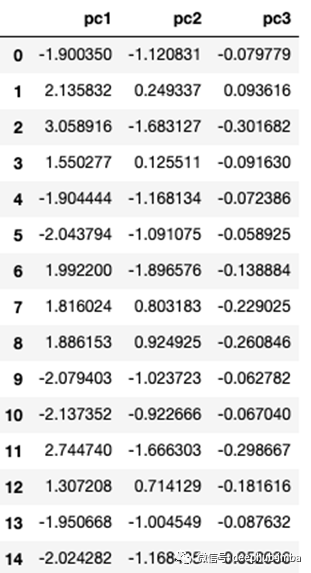
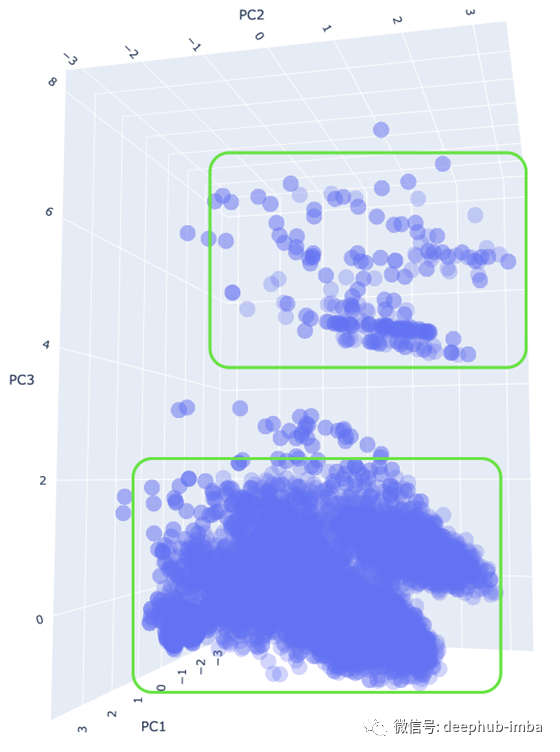
在3D空间中绘制数据,可以看到DBSCAN存在一些潜在的问题。DBSCAN的一个主要缺点就是它不能准确地对不同密度的数据进行聚类,从下面的图中,我们可以看到两个不同密度的单独集群。在应用DBSCAN算法时,我们可能能够在数据点较少的聚类结果中找到不错的聚类方式,但在数据点较多的聚类中的许多数据点可能被归类为离群值/噪声。这当然取决于我们对epsilon和最小点值的选择。
Scene = dict(xaxis = dict(title = 'PC1'),yaxis = dict(title = 'PC2'),zaxis = dict(title = 'PC3'))trace = go.Scatter3d(x=pca_df.iloc[:,0], y=pca_df.iloc[:,1], z=pca_df.iloc[:,2], mode='markers',marker=dict(colorscale='Greys', opacity=0.3, size = 10, ))
layout = go.Layout(margin=dict(l=0,r=0),scene = Scene, height = 1000,width = 1000)
data = [trace]
fig = go.Figure(data = data, layout = layout)
fig.show()
3.DBSCAN聚类
方法1
在应用聚类算法之前,我们必须使用前面讨论过的“肘形法”来确定合适的epsilon级别。看起来最佳的值在0.2左右。最后,由于我们的数据有3个主成分,我们将把最小点标准设置为6。
plt.figure(figsize=(10,5))
nn = NearestNeighbors(n_neighbors=5).fit(pca_df)
distances, idx = nn.kneighbors(pca_df)
distances = np.sort(distances, axis=0)
distances = distances[:,1]
plt.plot(distances)
plt.show()
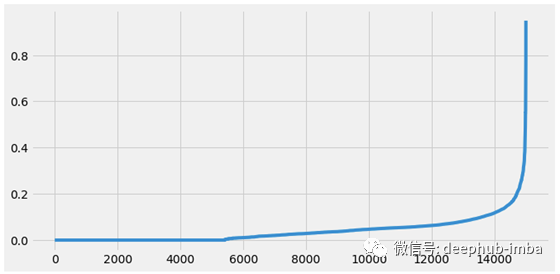
将epsilon设置为0.2,将min_samples设置为6,得到了53个集群,影像分数为-0.521,以及超过1500个被认为是离群值/噪声的数据点。在某些研究领域,53个集群可能被认为是有用的,但我们有一个15000名员工的数据集。从业务的角度来看,我们需要一些可管理的集群(即3-5个),以便更好地分配工作场所。此外,剪影得分-0.521表明数据点是不正确的聚集。
看看下面的3D图,我们可以看到一个包含了大多数数据点的集群。出现了一个较小但很重要的聚类簇,但剩下52个聚类簇的规模要小得多。从业务角度来看,这些集群提供的信息不是很多,因为大多数员工只属于两个集群。组织希望看到几个大的集群,以确定它们的有效性,但也能够从事一些针对集群员工的组织主动性工作(例如。增加培训、薪酬变化等)。
db = DBSCAN(eps=0.2, min_samples=6).fit(pca_df)
labels = db.labels_# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1if-1inlabelselse0)
n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d'%n_clusters_)
print('Estimated number of noise points: %d'%n_noise_)
print("Silhouette Coefficient: %0.3f"%metrics.silhouette_score(pca_df, labels))

Scene = dict(xaxis = dict(title = 'PC1'),yaxis = dict(title = 'PC2'),zaxis = dict(title = 'PC3'))labels = db.labels_trace = go.Scatter3d(x=pca_df.iloc[:,0], y=pca_df.iloc[:,1], z=pca_df.iloc[:,2], mode='markers',marker=dict(color = labels, colorscale='Viridis', size = 10, line = dict(color = 'gray',width = 5)))
layout = go.Layout(scene = Scene, height = 1000,width = 1000)
data = [trace]
fig = go.Figure(data = data, layout = layout)fig.update_layout(title='DBSCAN clusters (53) Derived from PCA', font=dict(size=12,))
fig.show()
Imageforpost
方法2
我们不使用“肘部方法”和最小值启发式方法,而是使用迭代方法来微调我们的DBSCAN模型。在对数据应用DBSCAN算法时,我们将迭代一系列的epsilon和最小点值。
在我们的例子中,我们将迭代0.5到1.5之间的epsilon值和2-7之间的minPts。for循环将使用这组值运行DBSCAN算法,并为每次迭代生成集群数量和影像分数。请记住,您需要根据数据调整参数。您可能会在一组参数上运行此代码,并发现产生的最佳影像分数是0.30。为了将更多的点包含到一个集群中,您可能需要增加值。
pca_eps_values = np.arange(0.2,1.5,0.1)
pca_min_samples = np.arange(2,5)
pca_dbscan_params = list(product(pca_eps_values, pca_min_samples))pca_no_of_clusters = []
pca_sil_score = []
pca_epsvalues = []
pca_min_samp = []forpinpca_dbscan_params:
pca_dbscan_cluster = DBSCAN(eps=p[0], min_samples=p[1]).fit(pca_df)
pca_epsvalues.append(p[0])
pca_min_samp.append(p[1])pca_no_of_clusters.append(
len(np.unique(pca_dbscan_cluster.labels_)))
pca_sil_score.append(silhouette_score(pca_df, pca_dbscan_cluster.labels_))pca_eps_min = list(zip(pca_no_of_clusters, pca_sil_score, pca_epsvalues, pca_min_samp))pca_eps_min_df = pd.DataFrame(pca_eps_min, columns=['no_of_clusters', 'silhouette_score', 'epsilon_values', 'minimum_points'])pca_ep_min_df
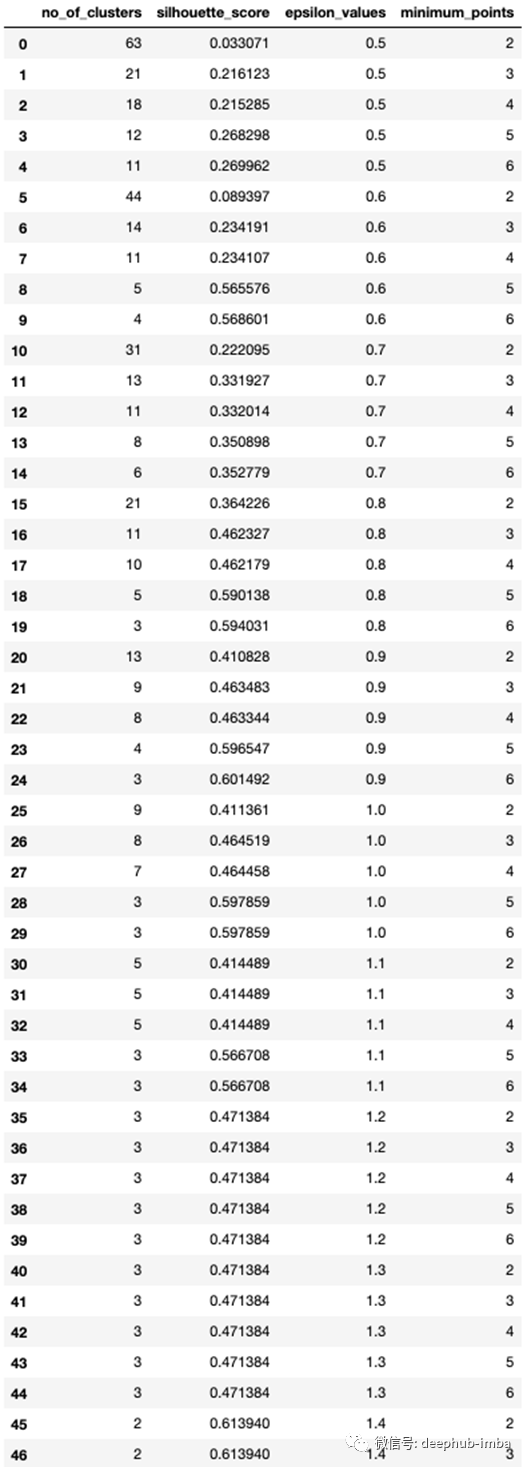
我们可以看到,通过我们的epsilon和minPts的迭代,我们已经获得了很大范围的簇数和影像分数。0.9到1.1之间的epsilon分数开始产生可管理的集群数量。将epsilon增加到1.2或更高会导致集群数量太少,无法在商业上发挥作用。此外,其中一些集群可能只是噪音。我们稍后会讲到。
增加的epsilon会减少集群的数量,但每个集群也会开始包含更多的离群点/噪声数据点,这一点也可以理解为有一定程度的收益递减。
为了简单起见,让我们选择7个集群并检查集群分布情况。(epsilon: 1.0和minPts: 4)。
同样重要的是,运行此代码串时肯定会遇到的一个常见错误。有时,当你设置的参数不合适,for循环最终会变成eps_values和min_samples的组合,这只会产生一个集群。但是,silhouette ette_score函数至少需要定义两个集群。您需要限制参数以避免此问题。
在上面的示例中,如果我们将epsilon参数的范围设置为0.2到2.5,那么很可能会生成一个集群并最终导致错误。
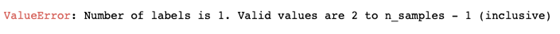
你可能会问自己“我们不是应该获得7个集群吗?”答案是肯定的,如果我们看一下独特的标签/集群,我们看到每个数据点有7个标签。根据Sklearn文档,标签“-1”等同于一个“嘈杂的”数据点,它还没有被聚集到6个高密度的集群中。我们自然不希望将任何“-1”标签考虑为一个集群,因此,它们将从计算中删除。
db = DBSCAN(eps=1.0, min_samples=4).fit(pca_df)
labels = db.labels_# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1if-1inlabelselse0)
n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d'%n_clusters_)
print('Estimated number of noise points: %d'%n_noise_)
print("Silhouette Coefficient: %0.3f"%silhouette_score(pca_df, labels))

set(labels)
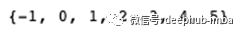
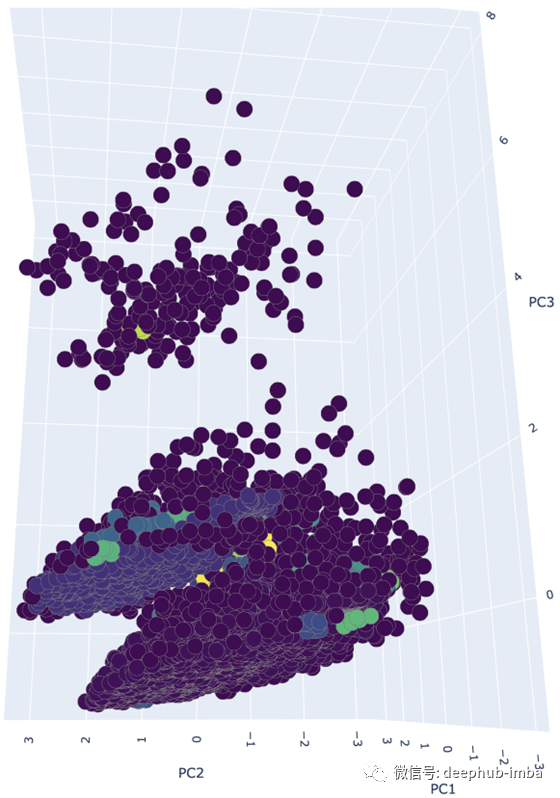
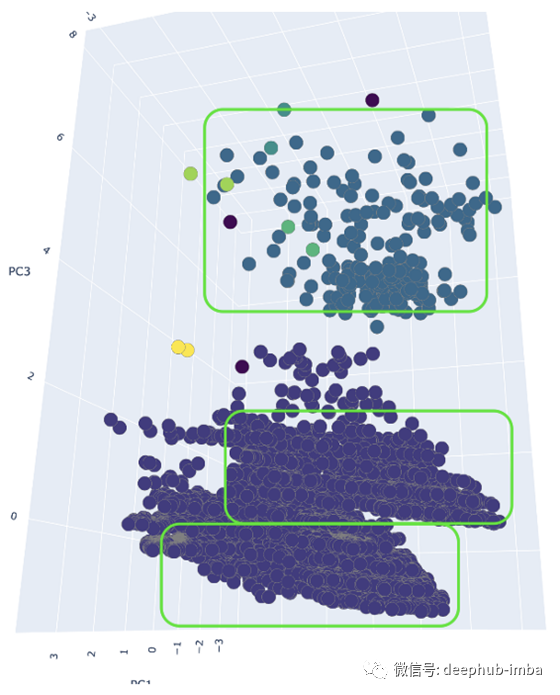
从6个DBSCAN派生集群的3D图中可以看出,尽管密度较小,但位于图顶端的密度较小的集群对DBSCAN并没有造成太大影响。如果您还记得的话,DBSCAN很难正确地集群各种密度的数据。顶部的集群和更大的底部集群之间的距离很可能大于1.0的epsilon值。
也就是说,数据集包含额外的高密度集群,但是我们的epsilon和minPts太大了。底部的聚类簇包含至少两个高密度的聚类簇,然而,由于底部聚类簇的高密度降低了epsilon和minPts,只会产生许多更小的聚类簇。这也是DBSCAN的主要缺点。我一直认为DBSCAN需要第三个参数“min_core”,它将确定一个集群可以被视为有效集群之前的最小核心点数量。
Scene = dict(xaxis = dict(title = 'PC1'),yaxis = dict(title = 'PC2'),zaxis = dict(title = 'PC3'))# model.labels_ is nothing but the predicted clusters i.e y_clusters
labels = db.labels_trace = go.Scatter3d(x=pca_df.iloc[:,0], y=pca_df.iloc[:,1], z=pca_df.iloc[:,2], mode='markers',marker=dict(color = labels, colorscale='Viridis', size = 10, line = dict(color = 'gray',width = 5)))
layout = go.Layout(scene = Scene, height = 1000,width = 1000)
data = [trace]
fig = go.Figure(data = data, layout = layout)fig.update_layout(title="'DBSCAN Clusters (6) Derived from PCA'", font=dict(size=12,))
fig.show()
在我们开始之前,让我们快速了解一下每个集群中的员工数量。似乎cluster 0包含了大部分信息不太丰富的数据点。事实上,如果我们使用0.5的epsilon值和5的minPts运行算法,就会产生63个集群,集群0仍然会包含99%的员工人口。
np.unique(labels, return_counts=True)
小结
DBSCAN,一种密度聚类算法,常用于非线性或非球面数据集。epsilon和minPts是两个必需的参数。epsilon是附近数据点的半径,这些数据点需要被认为是足够“相似”才能开始聚类。最后,minPts是需要在半径内的数据点的最小数目。
在我们的示例中,我们试图根据工作特征对包含15,000名员工的数据集进行聚类。我们首先标准化了数据集以缩放特征。接下来,我们应用主成分分析将维度/特征的数量减少到3个主成分。使用“肘部法”,我们估计了0.2的epsilon值和6的minPts。使用这些参数,我们能够获得53个集群,1500个离群值和-0.52的影响分数。不用说,结果并不是很理想。
接下来,我们尝试了一种迭代的方法来微调epsilon和minPts。我们已经确定了epsilon值为1.0和minPts值为4。该算法返回6个有效的集群(一个-1集群),只有7个异常值,以及0.46的可观影像分数。然而,在绘制派生集群时,发现第一个集群包含99%的员工。从业务的角度来看,我们希望我们的集群能够更加均衡地分布,从而为我们提供关于员工的良好见解。
DBSCAN似乎不是这个特定数据集的最佳聚类算法。
作者:Kamil Mysiak
deephub翻译组:孟翔杰
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
喜欢就请三连暴击!********** **********