【数据结构与算法】排序（下篇）

🐱作者：一只大喵咪1201
🐱专栏：《数据结构与算法》
🔥格言：你只管努力，剩下的交给时间！

排序

在文章排序（上篇）中本喵详细讲解了，插入排序(包括直接插入排序，希尔排序)，选择排序(包括直接选择排序，堆排序)和交换排序(包括冒泡排序，快速排序)。

再次看下面这张图：

常见算法中还有一个归并排序本喵没有介绍，下面本喵就来讲解下归并排序是如何实现的。

⚽归并排序

⚾递归实现

基本思想：

• 归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。
• 将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

下面本喵来讲解下上述的概念是什么意思。

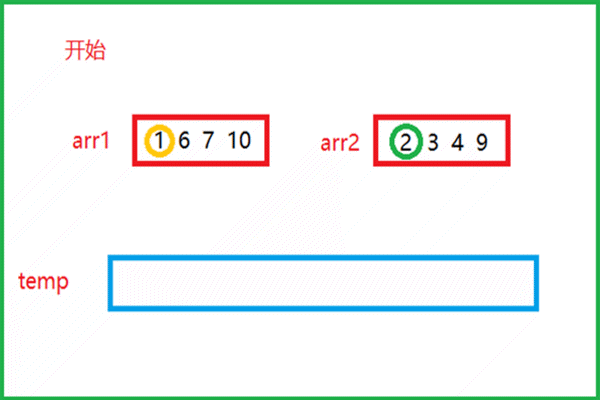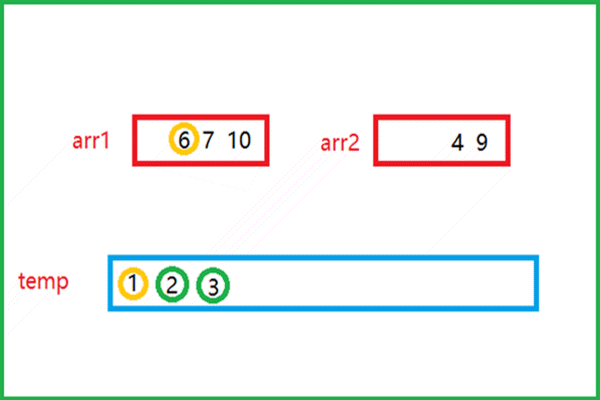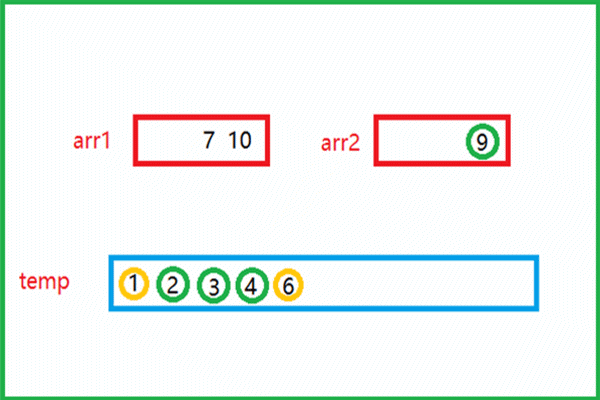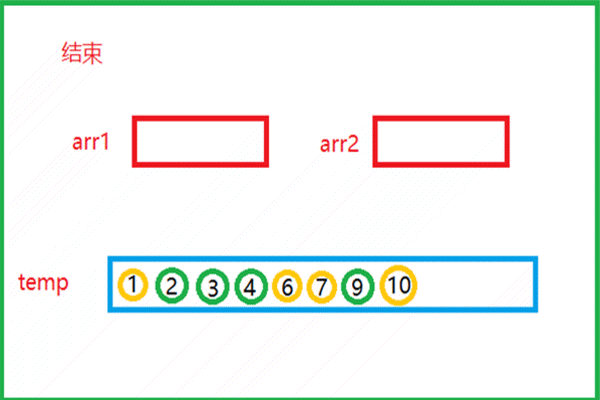
该动图就是归并思想的实现过程。

• 有俩个有序的数组arr1和arr2，比较俩个数组中的元素
• 较小的元素尾插到下面的临时数组temp中，再指向下一个元素与另一数组中的元素比较大小
• 如此重复，将俩个数组中的所有元素全部尾插到temp数组中
• 此时俩个有序的数组就归并为一个有序的数组

这种思想和链表的合并有相似之处。

但是我们往往拿到的数据并不是有序的，此时就要想办法让它成为俩个有序的数组来进行合并。

我们知道，单个的数据是一定有序的，我们就可以利用递归，将一组数据拆分到单个的数据为止，然后进行归并，归并后就成了两两有序，再次归并，直到所有的数据有序，采用的是二叉树的后序遍历的思想。

同样拿上面那组数据，但是它是乱序的，如：

10 6 7 1 3 9 4 2这一组数据，将它们进行升序排列，过程如下面动图：

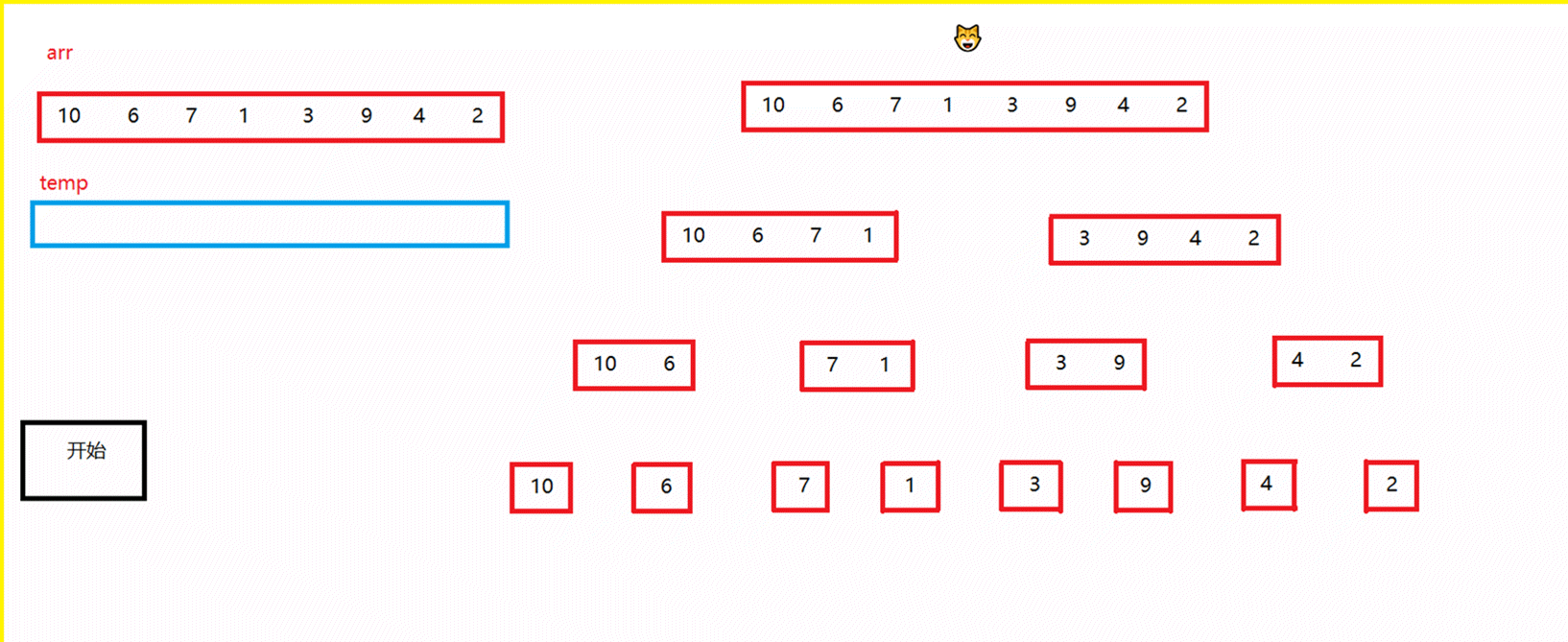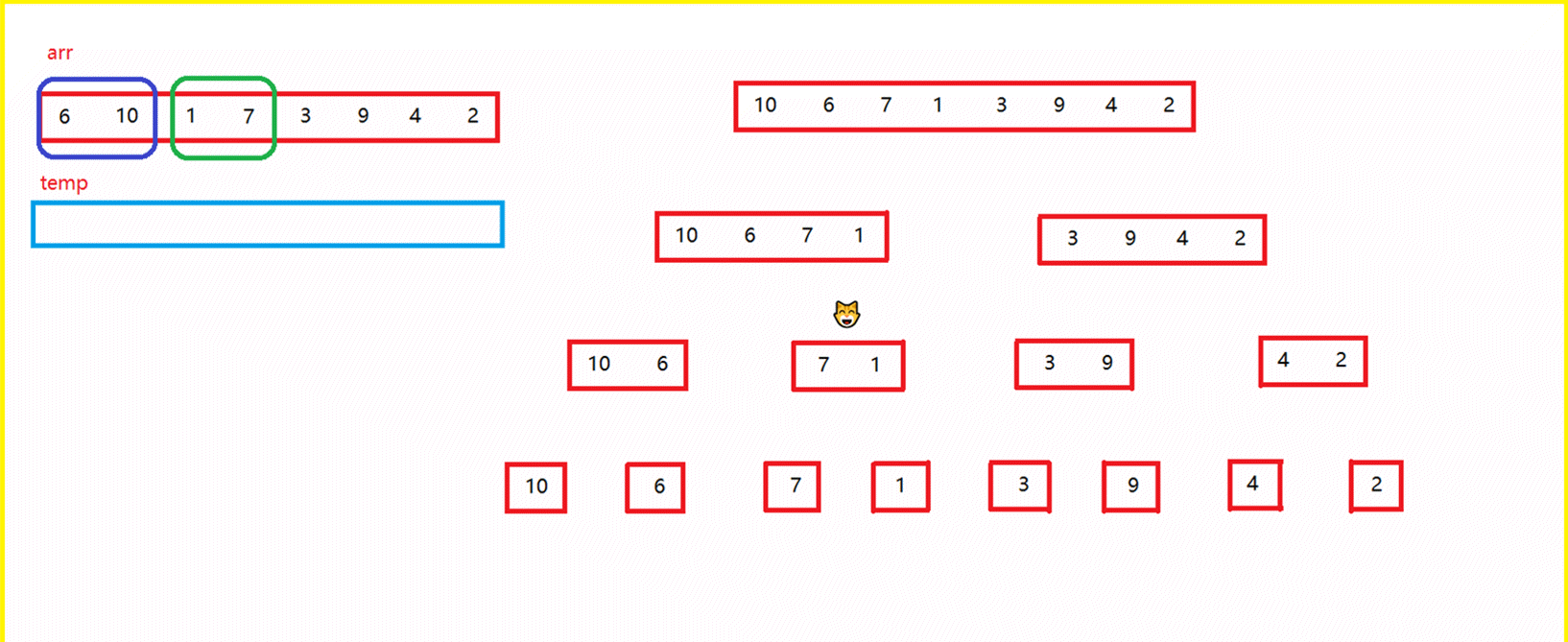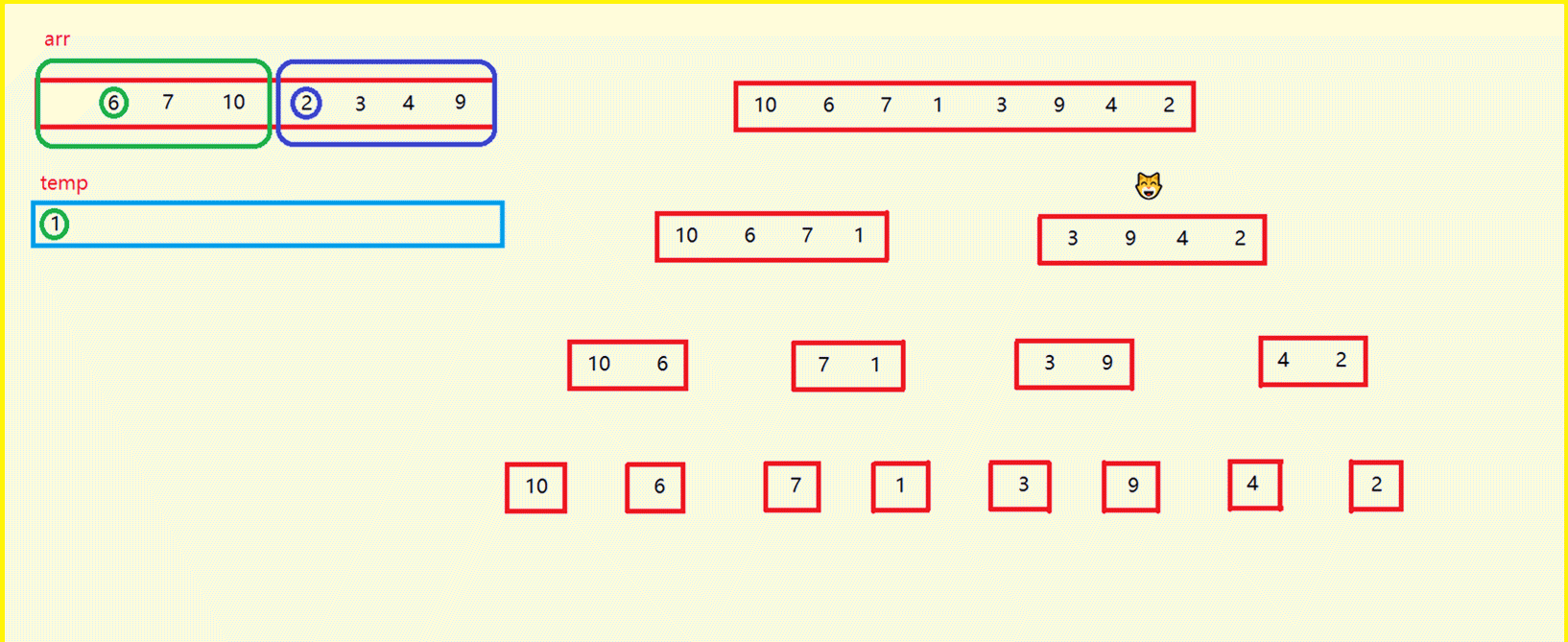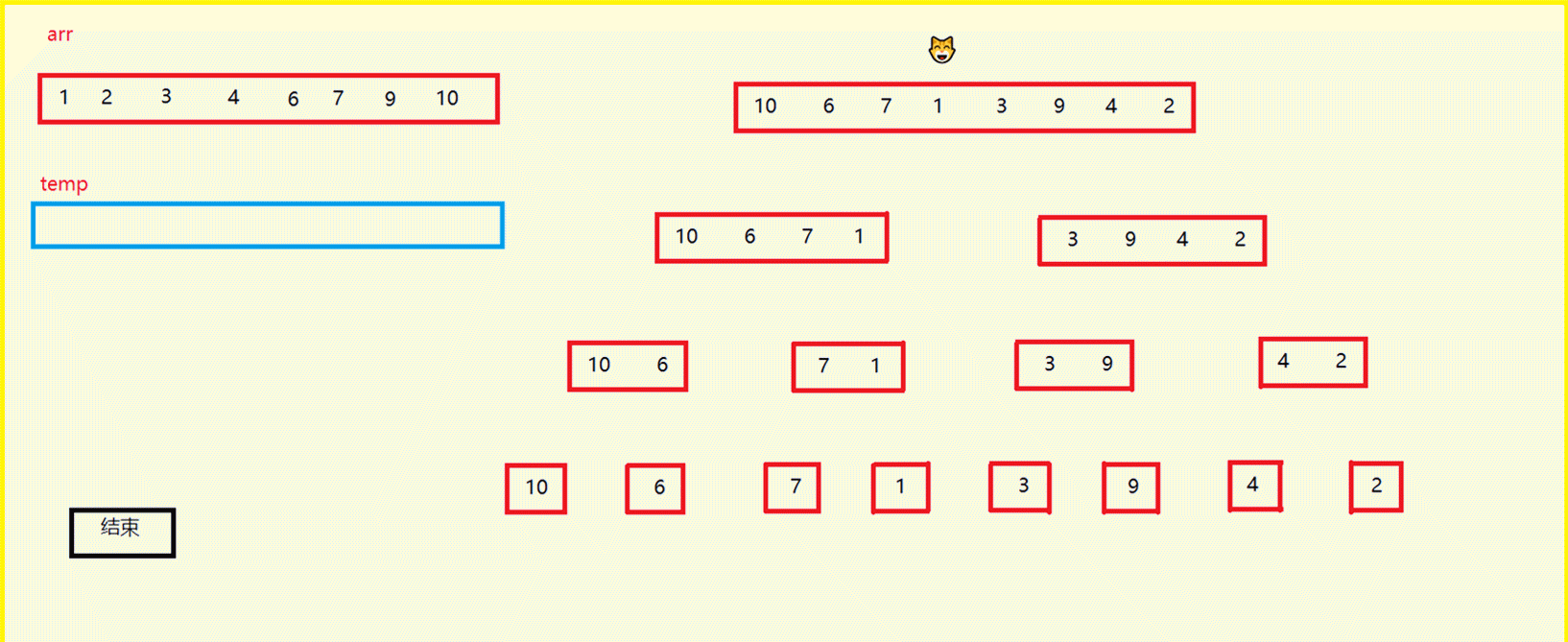
• 图中，猫头所走的路线就是递归的路线
• 左侧数组arr是原数组，temp是开辟的临时数组
• 使用下标将原数组采用递归的形式逐渐平分，分到俩个数组中只有1个元素的时候，进行归并
• 此时就有多个含有俩个元素的区间，再继续进行归并，直到所有元素升序排列。

代码实现：

看看用代码是如何实现上诉过程的：

staticvoid_MergeSort(int* a,int left,int right,int* temp){//结束条件,只有一个元素时返回if(left >= right)return;int mid =(right - left)/2+ left;//求中间元素下标//按区间[left,mid][mid+1,right]递归_MergeSort(a, left, mid, temp);_MergeSort(a, mid +1, right, temp);//归并int left1 = left, right1 = mid;int left2 = mid +1, right2 = right;int i = left;//比较将元素按照升序放在临时数组中while(left1 <= right1 && left2 <= right2){if(a[left1]<= a[left2]){
            temp[i++]= a[left1++];}else{
            temp[i++]= a[left2++];}}//一定有一个区间没有比较完，直接复制到临时数组中while(left1 <= right1){
        temp[i++]= a[left1++];}while(left2 <= right2){
        temp[i++]= a[left2++];}//拷贝回原数组memcpy(a + left, temp + left,(right - left +1)*sizeof(int));}//归并排序voidMergeSort(int* a,int n){//开辟临时空间int* temp =(int*)malloc(n *sizeof(int));if(temp ==NULL){perror("malloc fail");return;}//归并排序_MergeSort(a,0, n -1, temp);//释放空间free(temp);
    temp =NULL;}

可以看到，成功的将这组数字按照升序排列。

注意：

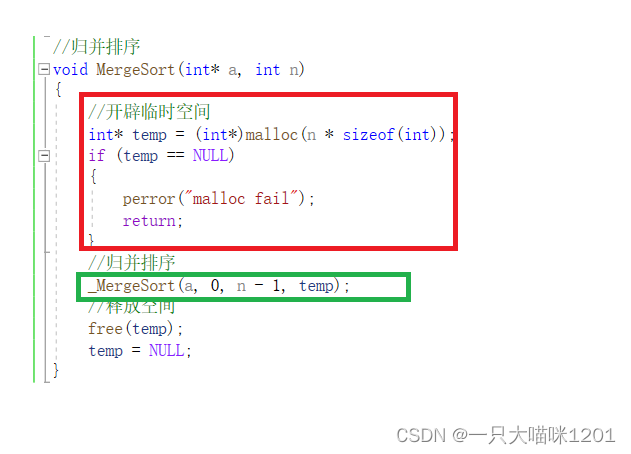
递归必须在另一个函数中实现，因为我们开辟了一组动态空间作为temp临时数组，如果递归不在另一个函数中实现，就会每递归调用一次该函数就开劈一次动态空间，造成空间的浪费。

• 通常在函数名前面加下划线_表示该函数的子函数。

• 红色框中是将一个数组分为俩个区间，[left , mid]和[mid+1 , right]
• 绿色框中就是递归调用的过程
• 蓝色框中是归并的过程的控制条件，在上面分为了俩个区间，在归并过程中记为[left1 , right1]和[left2 , right2]。 在归并中，一定是有一个区间中的元素全部放在零时数组中，一个区间中还剩有元素。 所以只要一个区间空了就要跳出循环归并。
• 黄色框只，由于我们并不直到是哪个区间中的元素还有剩余，所以进行俩个循环判断，符合就进循环，进去后将该区间中剩余的有序元素放在临时数组中
• 紫色框中是每归并完俩个区间后，将临时数组中的元素再拷贝回原来的数组，此时原数组中拷贝进来的元素就是有序的。

下面动图展示了数据的位置变化：

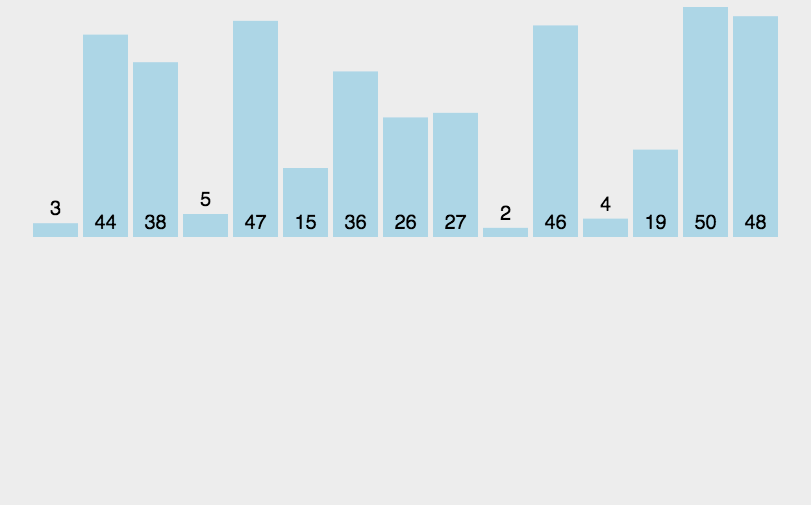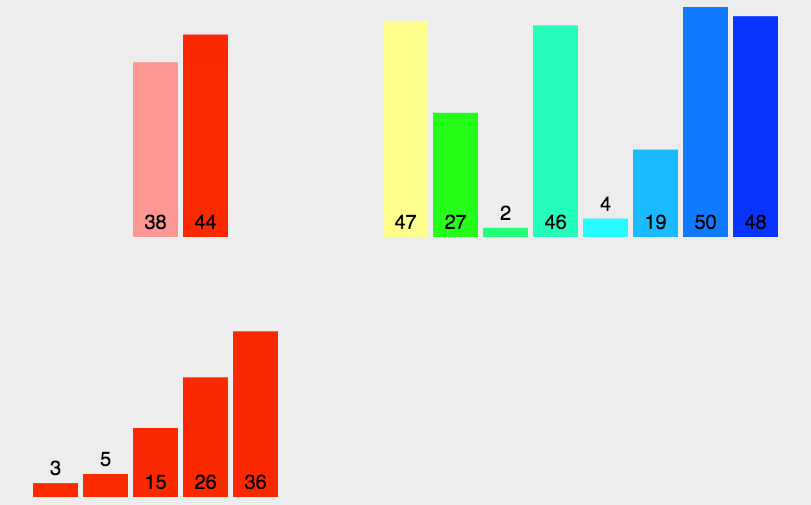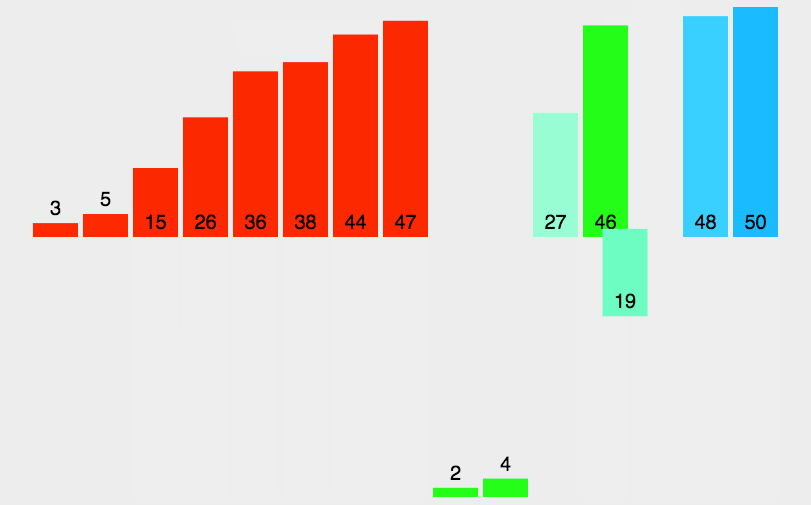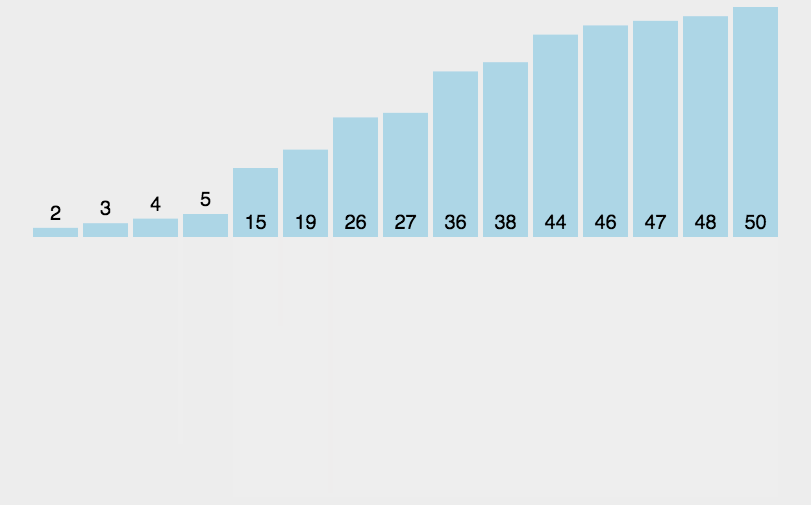
⚾非递归实现

上面是使用递归实现的归并排序，也是大多数情况下所使用到的，和快速排序一样，归并排序同样可以使用非递归的方法，这样就可以避免栈溢出。

基本思想：

1. gap = 1

将待排数据分为多个区间，每个区间中只有一个数据，每俩个区间形成一对，进行一次归并排序，假设一共有n个数据，此时就需要归并n/2次，其中gap表示区间中数据的个数。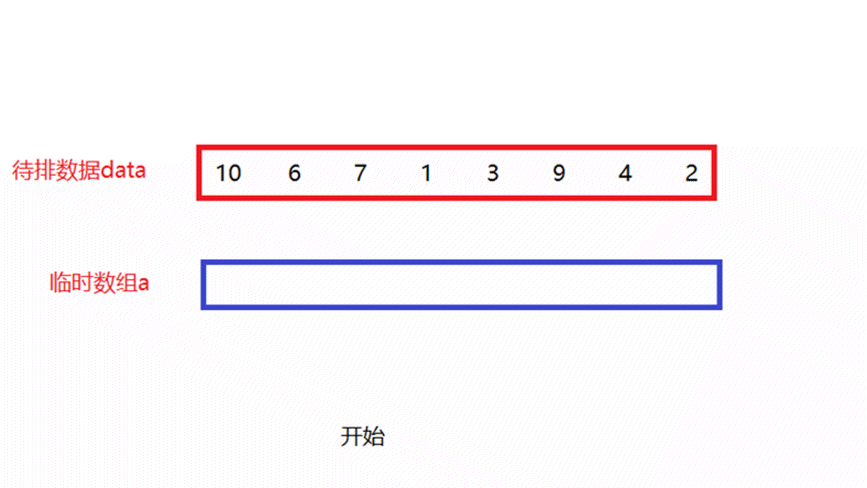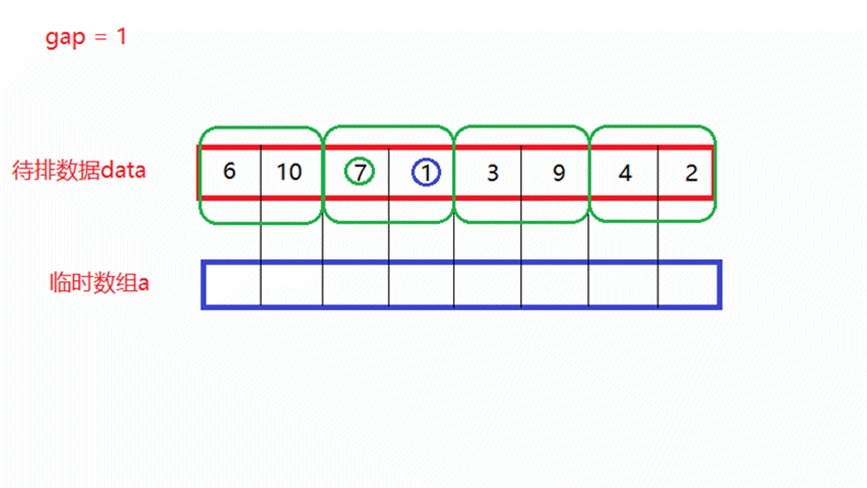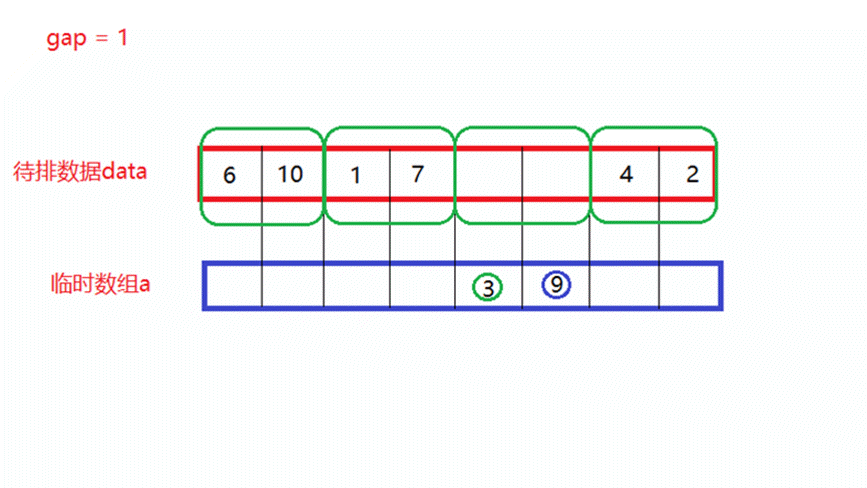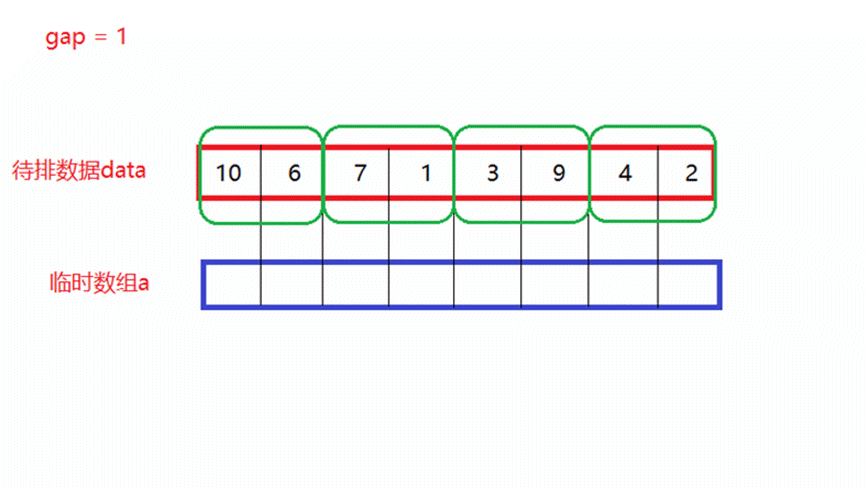

如上面动图所演示，当归并n/2次以后，每俩个数所形成的新区间就是有序的。

1. gap = 2

将gap = 1归并完成的待排数据，再分为多个区间，每个区间中有俩个数据，每俩个区间形成一对，进行一次归并排序，此时就需要归并n/4次。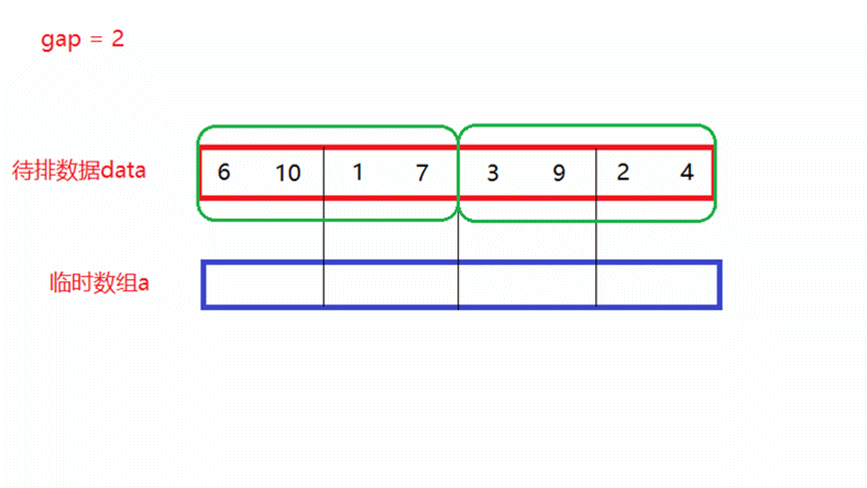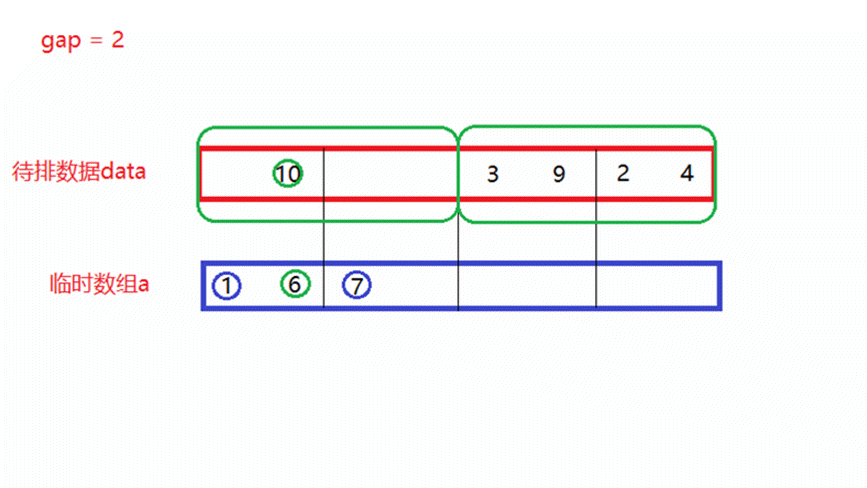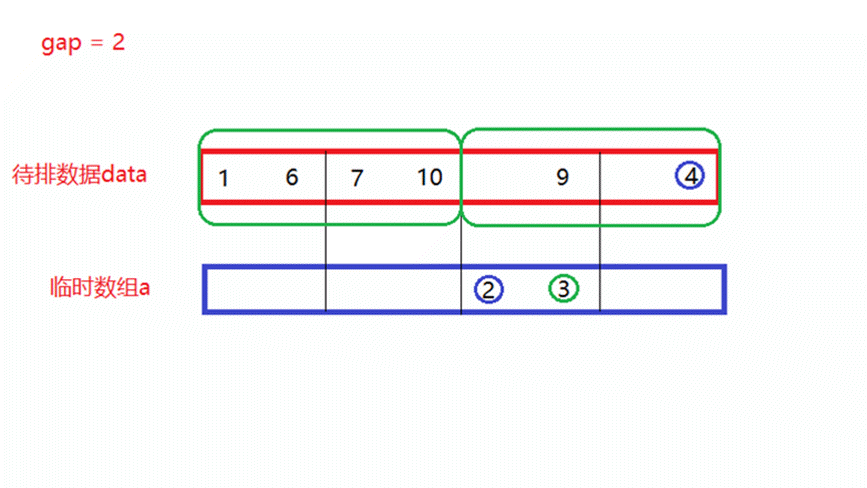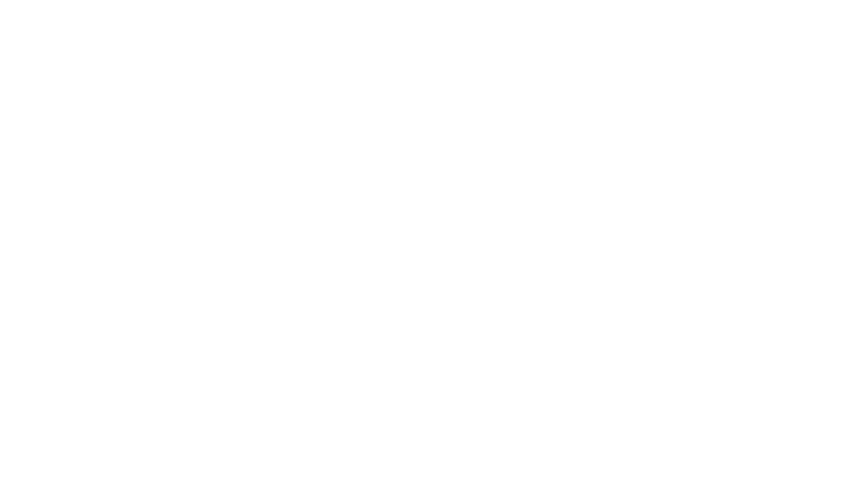

如上面动图所演示，当归并n/4次以后，每4个数所形成的新区间就是有序的。

1. gap = 4

将gap = 2归并完成的待排数据，再分为多个区间，每个区间中有4个数据，每俩个区间形成一对，进行一次归并排序，此时就需要归并n/8次。

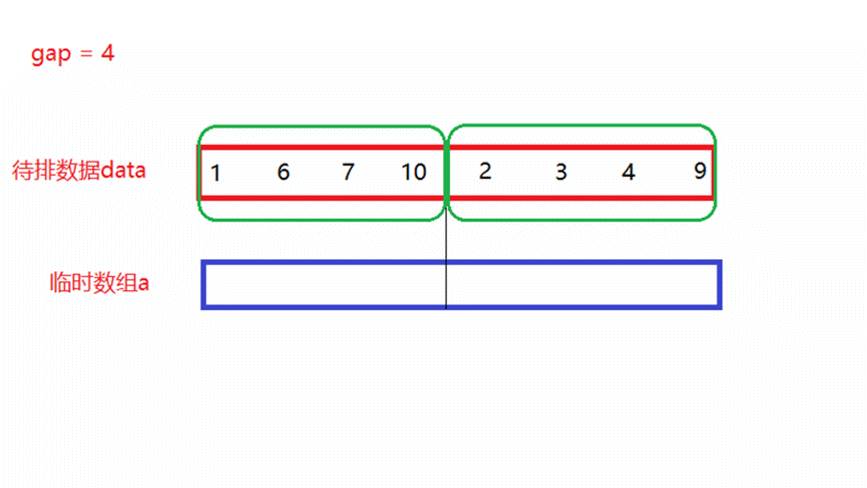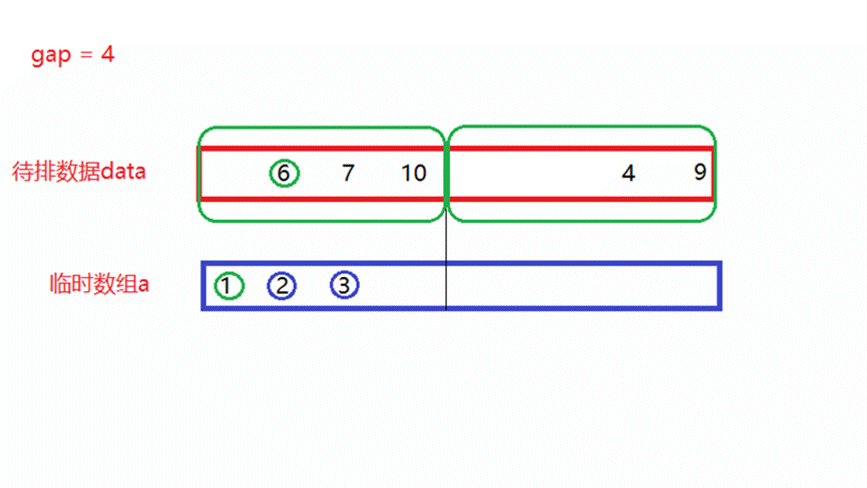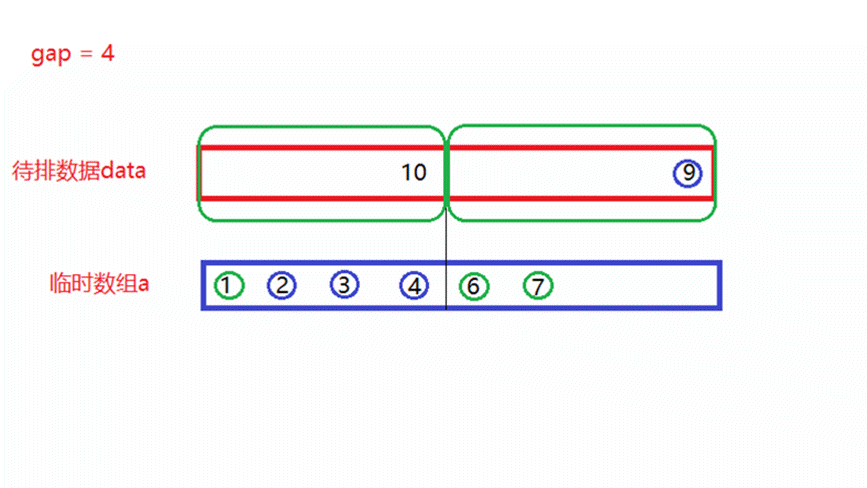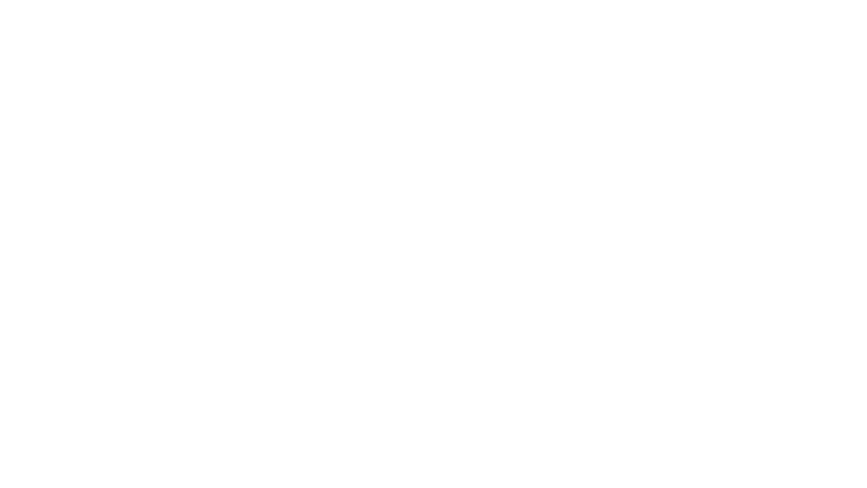
如上面动图所演示，当归并n/8次以后，每8个数所形成的新区间就是有序的。

1. gap = 8

如此重复，直到gap等于待排数据的个数为止，用前面的例子就是当gap等于8的时候停止。

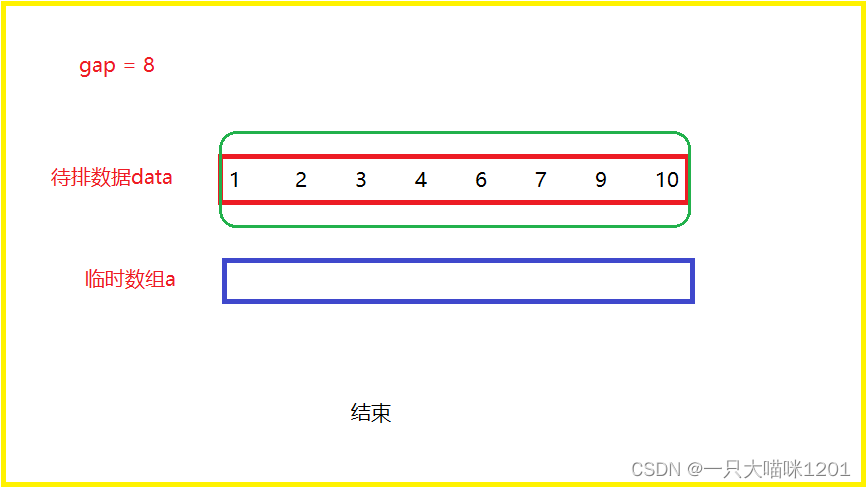
此时归并停止，并且数据已经按照升序排列好了。

代码实现：

//归并排序非递归voidMergeSortNonR(int* a,int n){//开辟临时空间int* temp =(int*)malloc(sizeof(int)* n);if(temp ==NULL){perror("malloc fail");return;}//归并int gap =1;while(gap < n){int i =0;for(int j =0; j < n; j +=2* gap){int left1 = j, right1 = j + gap -1;int left2 = j + gap, right2 = j +2* gap -1;//比较将元素按照升序放在临时数组中while(left1 <= right1 && left2 <= right2){if(a[left1]<= a[left2]){
                    temp[i++]= a[left1++];}else{
                    temp[i++]= a[left2++];}}//一定有一个区间没有比较完，直接复制到临时数组中while(left1 <= right1){
                temp[i++]= a[left1++];}while(left2 <= right2){
                temp[i++]= a[left2++];}//拷贝回原数组memcpy(a + j, temp + j,(2* gap)*sizeof(int));}
        gap *=2;}//释放动态空间free(temp);
    a =NULL;}

可以看到，已经实现了升序排列。

缺陷修复：

但是将上面那组待排数据稍加修改后我们再看效果，修改后的数据为：10 6 7 1 3 9 4 2 5，我们再看运行结果：

可以看到，程序直接崩了，这是什么原因呢？

我们只是将原本的待排数据又增加了一个，原本偶数个数据变成了奇数个数据，是奇数的原因吗？

我们在将待排数据增加一个，10 6 7 1 3 9 4 2 5 6，再看运行结果：

程序同样是崩溃的，说明和待排数据的个数是奇数个还是偶数个是没有必然关系的。

我们将每次归并的区间打印出来

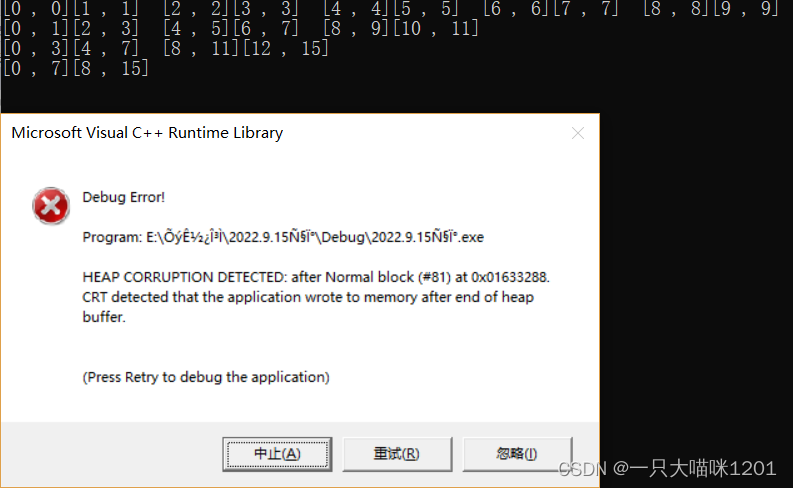
虽然程序是崩溃的，但是我还是可以看到归并的区间，下面就来分析一下这些归并的区间。

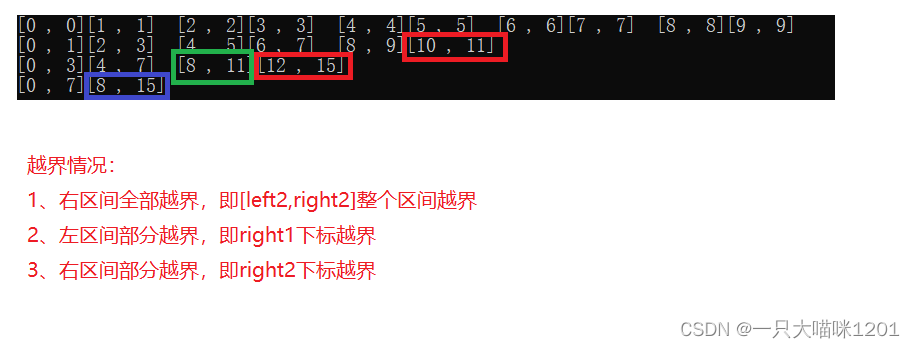
• 其中被框住的区间是存在越界的区间，它们的越界情况也无非就是上图中所写的3种，只要对这三种情况进行控制就可以了
• 右区间全部越界，此时的left2肯定是大于等于n(待排数据个数的)，所以就没有存在的必要，我们也就不对右区间进行归并了。
• 左区间部分越界，此时的right1肯定是大于等于n的，并且右区间肯定也是越界的，所以就没有存在的必要，我们也就不对右区间进行归并了
• 右区间部分越界，此时的right2肯定是大于等于n的，只需要将right1修正到n-1

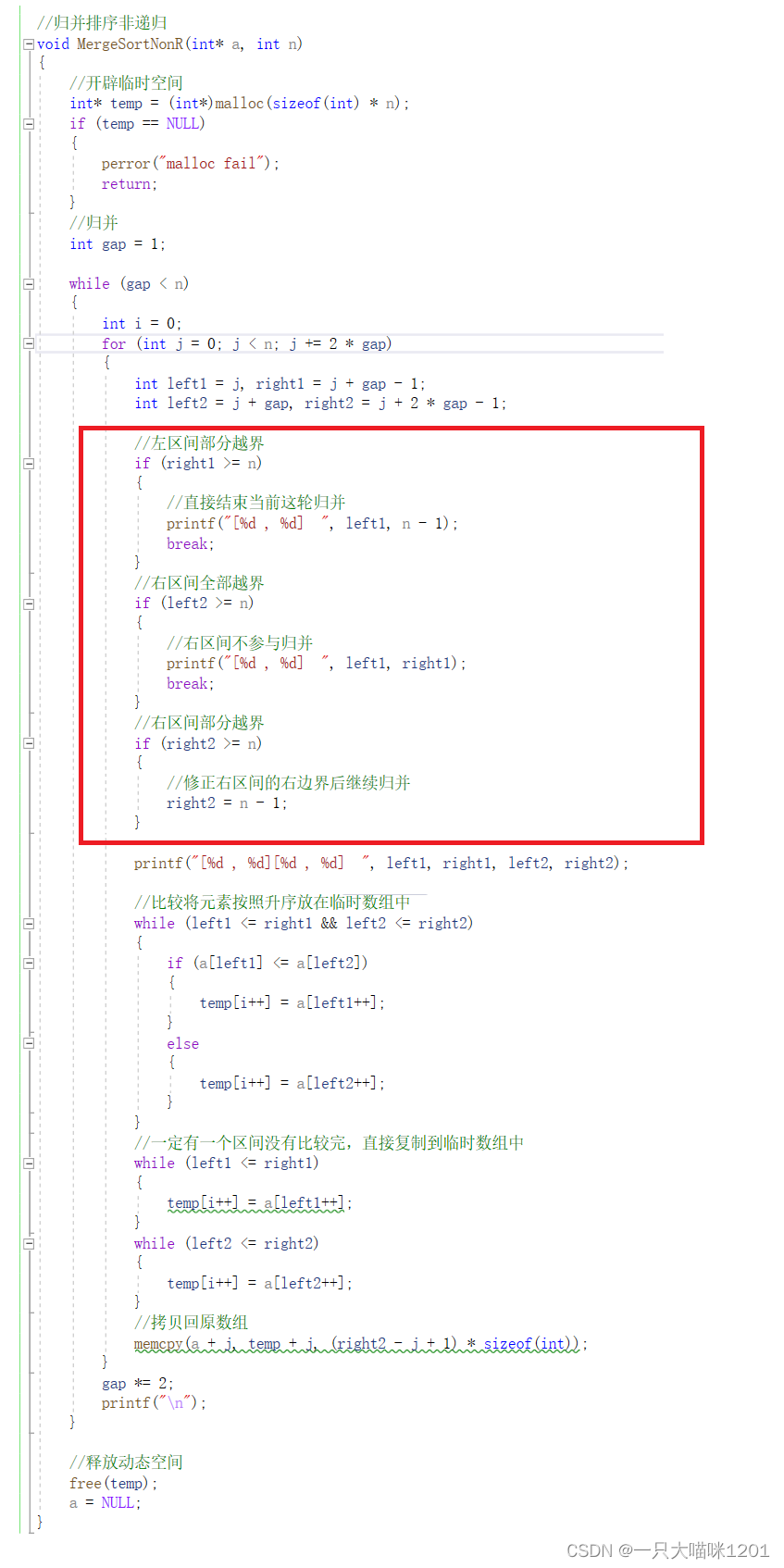
红色框中的内容就是对越界情况的修正。
此时就可以达到我们排序的目的了：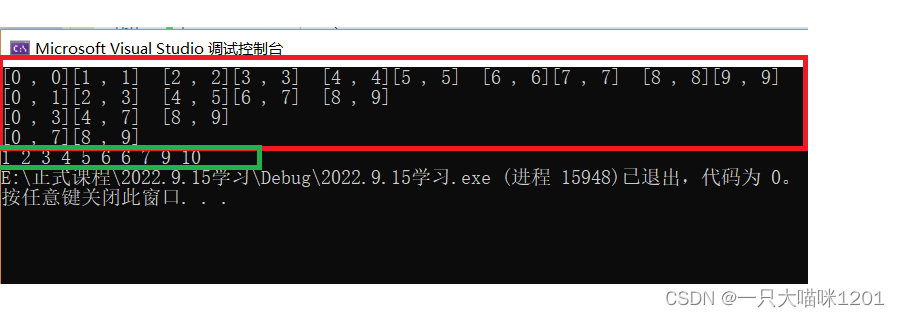

红色框中是进行归并的区间，绿色框中是待排数据按照升序排列后的结果。

⚽常见排序算法的复杂度和稳定性分析

⚾稳定性

• 稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

例如这样一组数据5 6 8 4 5 2 3 1 4，将相同关键字用不同颜色标记出来。

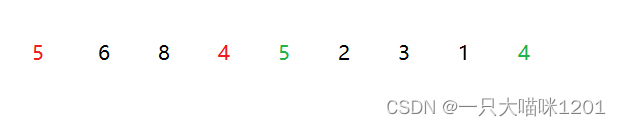
• 在排序之前，红色的5在绿色的5之前
• 红色的4在绿色的4之前

首先用归并排序按照升序来排列一下这组数据。

排好之后，该组数据变成了升序排列。并且

• 红色的5仍然在绿色的5之前
• 红色的4仍然在绿色的4之前

这样的排序算法，我们称之为稳定的排序算法。

同样是这组数据，我们用堆排序升序排列。

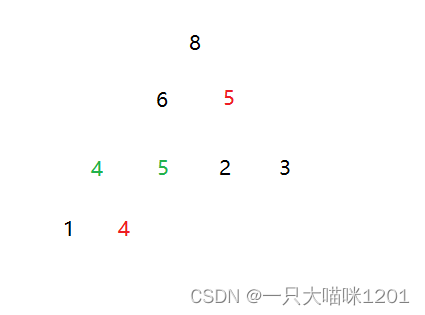
在向下调整建立大根堆的过程中，如果关键小于等于子节点时交换，那么在建堆的过程中就造成了不稳定。

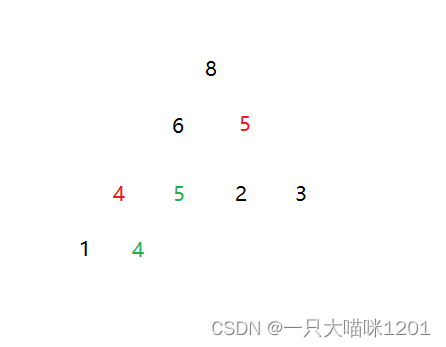
在向下调整建立大根堆的过程中，如果关键小于子节点时交换，那么在建堆后的数据仍然是稳定的。

我们使用建堆后仍然稳定的大根堆进行排序。

在交换堆顶和最后一个元素后进行向下调整时，通过控制，进来保证数据的稳定，让红色关键字放在绿色关键字之后，因为堆顶元素会去数组的最后面。

交换后并且进行向下调整后。

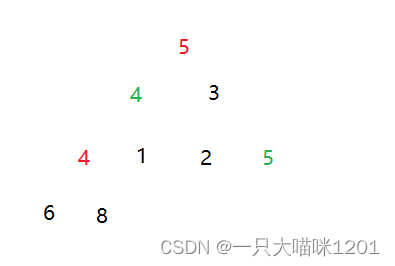
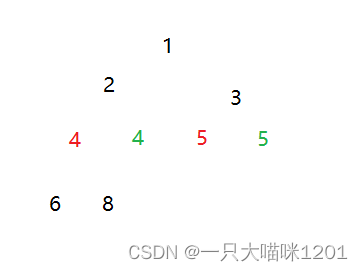
虽然这里可以通过控制将红色关键字放在绿色关键字前面，这是由于我们可以直观的看到关键字的颜色，从而进行控制。

而在编写程序过程中，我们是不知道关键字的颜色的，所以也无法控制它们的相对位置，所以堆排序是不稳定的。

现在已经知道了稳定性指的是什么，接下来我们分析一下这些常用排序算法的优略，通过复杂度和稳定性。

⚾具体分析

1. 插入排序

直接插入排序：

• 通过直接插入排序的思想我们知道，该算法最好情况下的时间复杂度是O(N)，此时数据是非常有序的，最坏情况的时间复杂度是O(N2)，此时数据是逆序的，空间复杂度是O(1)。
• 只需要控制end+1指向的元素放在[begin , end]区间与之相等的元素后面，该算法中关键字的相对位置就不会发生变化，所以该算法是稳定的。

希尔排序：

• 通过上篇文章中堆希尔排序的分析，该算法的平均时间复杂度是O(N1.3)，空间复杂度是O(1)。
• 由于相同的关键字可能会因为不同的间隙gap分在不同的组中，所以相对位置就会发生改变，而且像堆排序一样，我们在写程序的时候不知道关键字的相对位置，所以无法像直接插入排序那样只需要通过简单的控制就能稳定，所以该算法是不稳定的。

1. 选择排序

直接选择排序：

• 通过直接选择排序的思想我们知道，该算法是不分好坏情况的，它的时间复杂的是O(N2)，空间复杂度是O(1)。

很容易有一个误区，认为该算法是稳定的，其实它是不稳定的，我们来看这样一组数据：

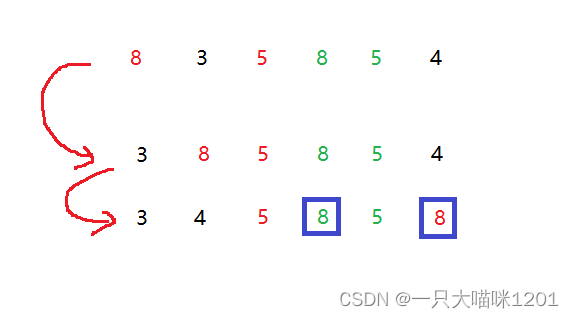
• 关键字5的相对位置是不会改变，但是关键字8的相对位置在无意中已经改变了，而且是无法控制的，所以直接选择排序是不稳定的。

堆排序：

• 根据堆排序的思想我们知道，建堆的过程时间复杂度是O(N)，每交换一次堆顶和最后一个元素后向下调整的时间复杂度是O(logN)，因为二叉树的高度是logN，一共有N个元素，所以堆排序的时间复杂度是O(N*logN)，不区分最好和最坏的情况。空间复杂度是O(1)，在原来的物理空间上操作。
• 在讲解稳定性的概念时本喵就分析过，堆排序是不稳定的。

1. 交换排序：

冒泡排序：

• 根据冒泡排序的思想，最好情况也就是非常有序时，时间复杂度是O(N)，只需要进行一趟就可以，最坏情况是逆序时，时间复杂度是O(N2)，空间复杂度是O(1)，是在原来空间上进行操作的。
• 只需要控制相等的关键字不发生交换，就可以达到稳定，所以该算法是稳定的。

快速排序：

• 根据快速排序的思想，无论采用hore版本，还是挖坑法，亦或是前后指针法，key位置如果选最左边的数据或者最右边的数据，在递归时，二叉树的深度是N，每层进行一趟，将一个数放在它所属的位置，需要进行N次交换，所以最坏情况下的时间复杂度是O(N2)，最好情况是将key位置采用三数取中或者随机取值的方法，此时递归的二叉树高度是logN，最好情况的时间复杂度是O(N*logN)，
• 由于递归在调用函数的过程中开创建栈帧，又因为函数的栈帧空间是可以重复利用的，所以空间复杂度是O(N)。
• 由于每趟快排中，key位置的元素最后的位置是不确定的，也无法进行控制，所以该算法是不稳定的。

1. 归并排序

• 根据归并排序的思想，递归二叉树的高度是logN，每一层都需要进行N次归并，将数据按照大小关系尾插到临时数组中，所以该算法的时间复杂度是O(N*logN)，由于需要开辟临时数组，所以空间复杂度是O(N)。
• 只需在归并的过程中，将左边区间和右边区间中的相同关键字按照先尾插左边关键字，再尾插右边关键字的顺序，就可以使该算法稳定，所以该算法是稳定的。

上诉内容可以总结为下面的表格：

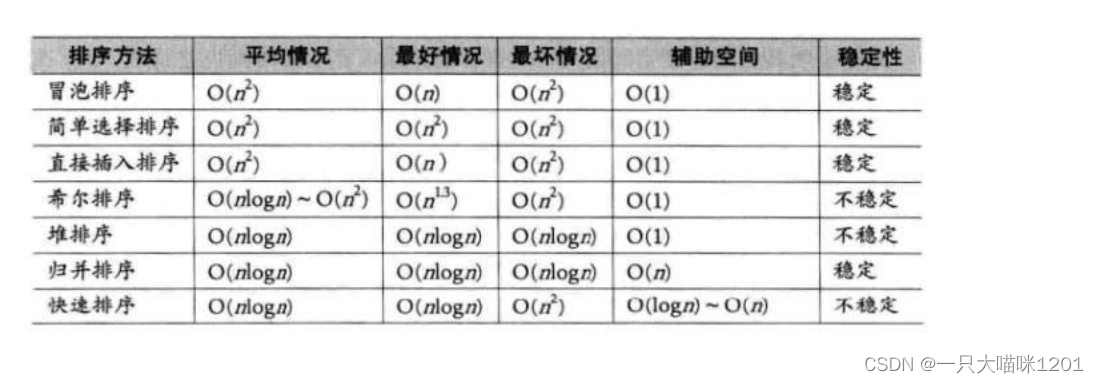
只要理解了这几种算法是思想，它们的时间复杂度和空间复杂度以及稳定性是很容易得出的。

⚽非比较排序

上面所讲述的排序方法都是通过比较俩个数的大小，再移动相应的数据达到目的的，属于比较排序的范畴，当然，还有一些非比较排序，这里本喵介绍俩个。

⚾计数排序

思想：

计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用，将待排数据中的每一个数据都映射一个地址，地址所对应的数据出现一次，将该地址中的内容加1，最后按照地址中数据的个数将数据还原到原来的数组。

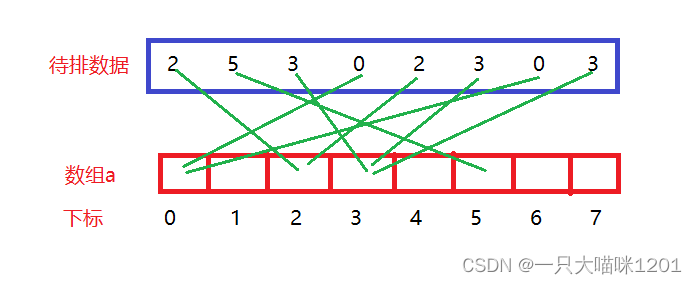
• 蓝色框中是待排数据，红色框是创建的一个数组，也就是映射的地址
• 待排数据中的每一个数据都对应一个数组中的地址
• 得出数据映射在数组中的下标后，该数据每出现一次，数组中该下标位置的内容加1，当然，数组a要全部初始化为0。
• 当待排数据全部映射到数组a中后，遍历数组中的元素，当数组中某下标i中的内容不是0时，说明映射的数存在
• 数组中不为0的位置中，数字是多少，就在原数据空间中按顺序覆盖多少个映射的数据。
• 当数组遍历完后，待排数据也就排好了。

这种方法中，每一个待排数据都有一个映射地址，也就是对应一个数组元素，而且数组中的下标是从0开始的，这样的映射被叫做绝对映射。如果待排数据是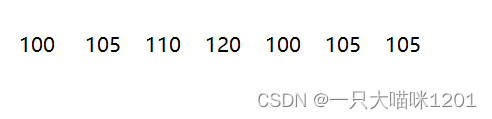

这样一组数据呢？映射的数组的下标还是从0开始吗？如果从0开始会造成空间浪费，所以我们需要开辟一个(max - min + 1)个空间的数组进行映射，其中max和min是待排数据的最大值和最小值。

• 设待排数据中的最小数据是min，则待排数据中的任意一个数据在数组中映射的下标是data-min。
• 反求待排数据的关系是(下标i+待排数据的最小值min)。
• 其他操作同绝对映射一样。

这样开辟一个范围的数组进行映射的方式称为相对映射。

我们将上面举列中的这组数据100 105 110 120 100 105 105进行升序排列。

分析：

• 待排数据data中的最大值max=120，最小值min=100
• 开辟大小为(max - min + 1)个元素大小的数组a，并且初始化为0
• 遍历待排数据data，每个数都在映射的数组中加1，也就是a[data[i]-min]++
• 当data遍历结束后，开始遍历数组a，只要a中某位置的元素不为0，就将对应下标i所映射的data中的数据(i + min)按顺序覆盖到原数组中
• 当数组a遍历结束后，原数组中的数据就按照升序排列好了。

代码实现：

//计数排序voidCountSort(int* data,int n){//寻找待排数据中的最小值和最大值int max = data[0];int min = data[0];for(int i =0; i < n; i++){if(data[i]> max)
            max = data[i];if(data[i]< min)
            min = data[i];}//开辟映射数组int range = max - min +1;int* a =(int*)malloc(sizeof(int)* range);if(a ==NULL){perror("malloc fail");return;}memset(a,0,sizeof(int)* range);//初始化为0//进行映射,个数统计for(int i =0; i < n; i++){
        a[data[i]- min]++;}//排序int j =0;for(int i =0; i < range; i++){while(a[i]--){
            data[j++]= i + min;//按照升序覆盖到原数组中}}//释放空间free(a);
    a =NULL;}

可以看到，成功的将该组数据按照升序排列了。

而且该算法可以实现负数的排序，因为相对映射得出的是一个相对值，是肯定大于等于0的。

注意：

1. 时间复杂度和空间复杂度

时间复杂度：

• 红色框中是寻找最大值和最小值的程序，该部分的时间复杂度是O(N)
• 绿色框中是遍历数组将映射值按升序还原到原数组中的程序，虽然是俩个循环，但是操作的数据一共是N个，所以该部分的时间复杂度是O(range)
• 所以计数排序算法的时间复杂度是O(N + range)
• 当range小于等于N的时候，该算法的时间复杂度就是O(N)
• 所以该算法的时间复杂度是取决于range的大小的，而range又取决于待排数据的离散程度，数据越离散，它的最大值和最小值的差就越大，所以对应的range也就越大。
• 所以说，计数排序适合用于待排数据比较紧凑的情况。

空间复杂度：

• 该算法开辟了range个临时空间作为待排数据的映射地址，所以空间复杂度就是O(range)

1. 稳定性

• 根据该算法的思想，它在按照映射数组还原待排数据的时候，是按照i + min的关系覆盖到原数组中的，这个过程中无法控制关键字的相对顺序，所以该算法也是不稳定的。

1. 弊端

• 在开辟作为映射地址的数组时，该数组的大小是根据待排数据中最大值和最小值之差确定的，所以待排数据只能是整型家族的数据
• 如果是字符串或者浮点型数据，是无法开辟出合适的映射数组的
• 所以说，计数排序只适用于整型数据的排序

⚽总结

上面内容加排序（上篇）便是常用的几种排序，重点在于理解各种排序方法的思想，从而知道它们的适用场景，在合适的场景中使用合适的排序方法可以提高程序的效率。在不知道用什么排序的时候，可以使用快排，俗话说，遇事不决用快排。