香农公式--通信的浅显理解--单纯只是为了弄懂功率和信道容量的关系

笔记的目标：简单梳理功率和信道容量的关系
其中主要是为了弄明白论文《Spectrum Sharing in Vehicular Networks Based on Multi-Agent Reinforcement Learning》中的应用场景问题，即功率（信道增益）与信道容量的关系
对于应用场景和其他公式的分析见我的此篇文章

香农公式

香农第二定理：信息传输率不超过信道容量就可以实现可靠传输

也就是说，我们如果希望实现可靠传输，就要知道信道容量是多少

信道容量有两种度量单位
一种是用每个符号能够传输的平均信息量的最大值C，一种是用单位时间（s）内能够传输的平均信息量的最大值Ct。在论文中选择的是第二种。

对于不同的连续信道和波形信道，它们存在的噪声形式不同，信道带宽及对信号的限制也不同，因此会具有不同的信道容量。

就比如在限带高斯白噪声加性波形信道中，对于单位时间信道容量的计算就是经典的香农公式

还有一个知识点，只是我不知道他和后面问题有没有联系，提前放在这里
信号
信号按照能量是否有限做区分，则有能量信号和功率信号。能量信号的能量等于一个有限的正值，但是平均功率为零；功率信号其平均功率等于一个有限的正值，但是能量为无穷大。

其中s(t)为代表信号电压或电流的时间波形

信号的基本知识

时域频域

对于信号特征的观察方式有两种，一种是在时域上，一种是在频域上，时域：x轴—时间t，y轴—电压/电流；频域：x轴—频率f，y轴—电压/电流，从时域到频域的转换就是傅里叶变换
而从频域到时域的转换就是傅里叶反变换

形象的观察见下图，图片来源，这篇文章解释了傅里叶变换以及信号在各种维度的观察，是真大佬，对于我一个外门汉极其友好。

能量信号和功率信号

信号在数学上可以用一个时间函数表示。确知信号(deterministic signal)是指其取值在任何时间都是确定的和可预知的，通常可以用数学公式表示它在任何时间的取值，例如，振幅、频率和相位都是确定的一段正弦波，它就是一个确知信号。

我们知道 : P=V2/R=I2R 即 功率 = 电压2/电阻=电流2x电阻
在通信理论中，通常把信号功率定义为电流在单位电阻（1Ω）上消耗的功率，即归一化功率P，因此在1欧姆阻抗前提下：P=V2=I2，功率 = 电压2=电流2

电压和电流的值随着时间变化而变化，因此将电压和电流的波形表示为函数𝑠(𝑡)

在高中学过能量的计算公式 E=I2Rt=V2t/R，在单位电阻的情况下 E=I2t=V2t，而对于随时间变化的电压电流，信号能量E应当是电流或者电压平方的积分，同时也是瞬时功率的积分

而信号的平均功率则定义为总功率在时间上的平均

信号按照能量是否有限做区分，则有能量信号和功率信号。能量信号的能量等于一个有限的正值，但是平均功率为零；功率信号其平均功率等于一个有限的正值，但是能量为无穷大。

总结一下就是
总能量（简称能量）是函数s2(t)的面积
平均功率（简称功率）是函数s2(t)的平均高度

频率还会有负值？

并且在这里记录一下我之前一直存在的疑问，因为有时候看到的频谱图是这样的

为什么频率还会有负值，这是我一直困惑不解的。
因为这个频率f指的不是物理意义上的频率，而是数学意义上的频率。根据傅里叶反变换式子可以看出傅里叶变换实际上并不是把实信号x(t)分解成一系列的正弦函数的相加，而是一系列复指数信号的相加（积分就是某种意义上的相加，离散是求和，连续是积分），而傅里叶变换后的频率恰恰指的是这些复指数信号的频率。所以说这里的频率f并不是指实信号x(t)中的频率。
那么既然频率f不是实信号x(t)中的频率，那它和x(t)中信号的频率有什么关系呢，欧拉公式给我们做出了说明：

从欧拉公式中可以看出，实信号中的一个频率在复指数信号中有一正一负频率与之对应。这样就能够从公式层面上解释了为什么傅里叶变换后会有和正频率对应的负频率了。所以在频谱分析的时候，频域上f，是复频域上的频率，而不是“实频域”上的频率。
如果还是不太理解，看一个直观的图理解欧拉公式

欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。

eit可以理解为一条逆时针旋转的螺旋线，那么e-it则可以理解为一条顺时针旋转的螺旋线。而 cos (t)则是这两条旋转方向不同的螺旋线叠加的一半，因为这两条螺旋线的虚数部分相互抵消掉了。这里，逆时针旋转的我们称为正频率，而顺时针旋转的我们称为负频率。

而通过各种公式的证明（见下图），可以得到结论：如果将数学上频谱函数的负频率分量和正频率分量的模相加，就等于物理上实信号的频谱的模。

一般称数学上的频谱函数为双边谱，而将实信号的频谱成为单边谱，前者用于数学分析，后者用于实验测量

这个证明在《通信原理》中有，放在这里

香农公式预备知识

信号的信息测度

信息量：

收到某信息获得的信息量 = 不确定性减少的量 =（收到消息前关于某件事的不确定性）-（收到消息后关于某件事的不确定性）
这里的信息量已经无法像上面的时域频域观察信号一样可以很形象化地观察了，这里对信息量的定义很抽象

自信息量𝐼(𝑎𝑖)：

事件𝑎𝑖发生所含的信息量𝐼(𝑎𝑖) = 𝑓[𝑃(𝑎𝑖)]

• 𝑃(𝑎𝑖) 是事件𝑎𝑖发生的先验概率
• 𝑓(𝑃𝑖)应该是先验概率𝑃(𝑎𝑖) 的单调递减函数，即当𝑃1(𝑎1) > 𝑃2(𝑎2)时，𝑓(𝑃1) < 𝑓(𝑃2)，因为如果某事件发生的概率很大，那么它的发生并不会带来意外，那么从这件事件的发生中获得的信息就很少
• 当𝑃(𝑎𝑖) = 1时， 𝑓(𝑃𝑖) = 0
• 当𝑃(𝑎𝑖) = 0时， 𝑓(𝑃𝑖) = ∞
• 两个独立事件的联合信息量应该等于它们分别的信息量之和，即统计独立信源的信息量等于它们分别的信息量
• 综上，可以从数学上证明这种函数形式是对数形式，即
• 𝐼(𝑎𝑖) 代表两种含义 – 当事件𝑎𝑖发生以前，表示事件𝑎𝑖发生的不确定性 – 当事件𝑎𝑖发生以后表示事件𝑎𝑖所含有（或所提供）的信息量
• 信息量𝐼(𝑎𝑖)的单位为比特（log的底为2），当底为e时单位为奈特，底为10时单位为哈特

这里的比特和计算机的比特含义不一样，这里的比特(bit binary unit)指的是抽象的信息量单位，而计算机中的比特的比特代表的时二元数字(binary digits)。这两种定义之间的关系是每个二元数字所能提供的最大平均信息量为1比特。

信息熵H(X)：

定义信息的数学期望为信源的平均自信息量

这里熵借用了物理中的热熵，因为这个表达式和物理中的热熵的表达式相似，在统计物理学中，热熵是一个物理系统杂乱性（无序性）的度量。熵：泛指某些物质系统状态的量度，系统内在的混乱程度

单位为 比特/符号

信息熵有三种物理含义：

• 信息熵𝐻(𝑋) 是表示信源输出后，每个消息（或符号）所提供的平均信息量
• 信息熵𝐻(𝑋) 是表示信源输出前，信源的平均不确定性
• 用信息熵𝐻(𝑋) 来表征变量X的随机性

这里有个跳跃，上面的自信息是事件的发生概率，还是离散的事件，怎么到了下面的信息熵就变成连续的变量了，这里做出解释。
连续的变量X可量化分层后用离散变量描述。量化单位越小，所得的离散变量和连续变量越接近。因此连续变量的信息测度可以用离散变量的信息测度来逼近

X位于第i区间的概率Pi是

这样连续信源X就可以被量化成离散信源

从物理意义上解释，X代表电压幅度，p(x)Δ代表电压幅度为X的概率
此时离散信源Xn的熵是

一般情况下，上式的第一项是定值，而当∆→0时，第二项是趋于无限大的常数，所以避开第二项，定义连续信源的熵为

由上式可知，所定义的连续信源的熵并不是真实信源的绝对熵，而是连续信源的绝对熵减去一个无穷大的常数项，因为连续信源取值连续，取某一个值的不确定性也为无限大，因此此时的熵表示相对性，称之为差熵（相对熵）

平均互信息I(X;Y)：

表示接收到输出符号后，平均每个符号获得的关于X的信息量

• 𝐼(𝑋; 𝑌) = 𝐻(𝑋) − 𝐻(𝑋|𝑌) = 𝐻(𝑌) − 𝐻(𝑌|𝑋)
• 𝐻(𝑋|𝑌)，条件熵也称信道疑义度，表示在输出端收到输出变量Y的符号后，对于输入端的变量X尚存在的平均不确定性（存在疑义）

信道

限带高斯白噪声加性波形信道（AWGN信道）

• 限带：通信系统或者传输信号被限制在某个频带范围之内。
• 高斯白噪声：在此频带范围之内，噪声的功率谱密度是常数，即为白噪声。这些噪声都是电阻性元器件中的电子的热运动，是热噪声，大量自由电子的运动特性服从高斯分布，因此又称为高斯白噪声。 • 运动特性服从高斯分布：时间连续的波形信号在某一时刻𝑡 = 𝑡0，信号的取值是连续的又是随机的，随机波形信源输出的消息可以用随机过程{x(t)}描述，这个随机过程的概率密度服从高斯分布
• 加性波形信道：信道中噪声对信号的干扰作用表现为与信号相加的关系，则此信道称为加性信道，此噪声为加性噪声，即输入和输出信号是随机过程{x(t)}和{y(t)}，而加入信道的噪声是加性高斯白噪声{n(t)}（其均值为零，功率谱密度为𝑁0 /2），所以输出信号满足{y(t)} = {x(t)} + {n(t)}
• 在加性连续信道中，信道的传递概率密度函数就等于噪声的概率密度𝑝(𝑦|𝑥) = 𝑝(𝑛)，进而可证明𝐻(𝑌|𝑋) = 𝐻(𝑁)，说明条件熵𝐻(𝑌|𝑋) 是由于信道中噪声引起的，它完全等于噪声信源的熵，称𝐻(𝑁)为噪声熵
• 功率谱密度𝑃(𝑓) = 𝑁0 /2 信号功率 平均功率

什么是功率谱密度：反应信号的功率在频域的分布情况

噪声信源——高斯信道{n(t)}

在上面说的信道中，噪声是高斯噪声，而噪声可以看作是一个专门制造噪声的信源在持续的发送信息，而高斯噪声具有下面所述的性质
基本高斯信源是指信源输出的一维随机变量N的概率密度分布是正态分布

噪声信源：随着时间变化；取值根据概率而定，是一个随机过程，对于本质是随机过程的高斯信源，可以根据下图进行理解，左边是电压函数n(t)随着时间的变化而变化，对于某时刻t1而言，它的取值也是不确定的（如果是确定的，那就是确知信号，而不是随机过程），因此它的取值是在t1时刻上进行上下浮动，具体会取何值，取值的大小根据概率而定，而连续随机变量的概率由概率密度确定，这个概率密度对于高斯信号而言就是高斯分布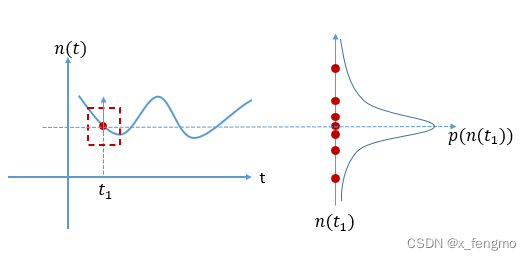

• 根据上面提到的信息熵的计算公式可以计算出噪声信源的信息熵
• 当均值𝑚 = 0时，X的方差𝜎2就等于信源输出的平均功率P，则ℎ(𝑁) =(1/2)𝑙𝑜𝑔2𝜋𝑒𝑃

关于如何将功率P和方差联系起来的，解释如下

第一个等号将p(n)代入就可以算出来，使用D(X)=E(X2)-E2(X)计算
第二个等号：确知信号(信号不是随机过程，虽然随着时间变化，但是确定某时刻的幅度就是多少)的平均功率是电压2的时间平均：
对于随机过程(不仅波形会随着时间变化，而且具体某时刻的取值也是不确定的，是随机变量)的信号，某一时刻的平均功率要取统计的平均，也就是所有可能波形在这一时刻的平均，对于某一时刻而言，取值也是随机的，

并且存在一个定理：若一个连续信源输出信号的平均功率被限定为P，则其输出信号幅度的概率密度分布时高斯分布时，信源有最大的熵，其值为(1/2)𝑙𝑜𝑔2𝜋𝑒P

这个定义会在后面的最大值计算中使用

这里讲一下为什么说通信里的噪声，一般指的是热噪声，是服从高斯分布的
通信系统中的主要噪声是热噪声，热噪声是由导体内电子热运动造成，存在于所有的电子设备和传输媒体中，是温度的函数。 热噪声均匀的分布在通信系统的整个频率范围内，因此称为白噪声。
“一大堆电子的热运动”，那根据中心极限定理，热噪声被建模成高斯随机过程，因为它由许多独立事件（单个电子的热波动）的叠加(superposition)组成

为什么这么定义(中心极限定理)，出处见此
John R. Barry; Edward A. Lee; David G. Messerschmitt (2004). Digital Communications. Sprinter. p. 69. ISBN 9780792375487.

对于叠加(superposition)，，因为原文并没有写明是求和(sum)，可能是相乘的叠加，也可能是相加的叠加，所以我去维基百科上搜了一下关于叠加在物理上的定义，见下图，指明了是求和，因此我下面进行猜测的时候才用的”叠加起来=平均值*N“这个说法

中心极限定理是什么
中心极限定理指的是给定一个任意分布的总体。每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。

我的理解是，如果某一时刻，在某导体内，所有电子（N个）在进行热运动，这就相当于对总体（还有除了本导体之外的其他电子）进行了样本为N的抽样。对于某一段时间来看，相当于由很多个时刻组成（当然时间是连续的，这里只是用离散的点去贴近连续的时间），假设由m个时刻组成，这就类似于每次抽取N个样本，抽取m次，而热噪声是多个单电子热运动叠加的（叠加起来=平均值*N），根据中心极限定理平均值接近正态分布，那么是不是也可以得到热噪声（即多个单电子热运动的叠加）也是接近正态分布的

抽样并联信道

通过抽样将连续信道转换为离散信道分析其容量特点，也就是分析他的随机过程的特点
一般信道的带宽（频率的范围）是有限的，设带宽为W(|f|<=W，单位Hz)，取样时间限制在（-T/2,T/2）内，对信道的输入、噪声和输出进行分别抽样。根据抽样定理，能不失真的还原波形的抽样率至少为2W。为使得到的离散时间子信道独立，抽样率为2W，那么抽样总点数为N=2TW。这样就构成一个由N个子信道组成的等价的离散时间并联信道。

• 该等价离散时间并联信道输入、噪声与输出序列分别为{𝑥𝑖}， {𝑦𝑖}，{𝑧𝑖}，𝑖 = 1, … , 𝑁，并且{𝑦𝑖} = {𝑥𝑖} + {𝑧𝑖}, 𝑖 = 1, … , 𝑁
• 如果𝑧(𝑡)是带宽为W的低通白噪声，则可以证明抽样后的𝑧𝑖是相互独立的
• 这样，通过时域抽样，原来的限带波形信道就变成一个等价的由N个离散时间独立子信道构成的并联信道

• 为什么带宽是有限的，大概理解一下就是，频率的大小和发射天线的长度有关，天线太短容易被遮挡，太长不现实，比如整一个和地球直径相等的天线的非常不现实，所以天线的高度限制了信号频率的范围
• 采样/抽样 是将一个信号（即时间或空间上的连续函数）转换成一个数值序列（即时间或空间上的离散函数）。采样过程所应遵循的规律，又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据
• 奈奎斯特抽样定理：若f(t)是一个频带限制在（0，fh）内的时间连续信号，要想抽样后的信号能够不失真地还原出原信号，则必须抽样频率fs大于或等于信号最高频率分量fh的两倍，或说信号的最高频率不得大于折叠频率fs/2，即fs≥2fh
• 证明在《通信原理》里面有，放在下面 如何抽样，使用冲激函数，做卷积（大概如此，非科班的理解），频域的卷积对应时域的乘积

大体解释一下什么意思，作为一名计算机人，类比计算机的知识就是，使用比如8bit可以确定一个波形，然后同一时间并列传输8bit信息，并行输出多bit（计算机组成原理里不是数据传输分并行和串行嘛，这个就相当于并行）

香农公式求解步骤

接下来就是使用上面的东西综合计算香农公式
香农公式用来求信道容量，此处对信道容量的定义： 用单位时间（s）内能够传输的平均信息量的最大值Ct

其中的C使用下列式子进行求解

这里的代入信息功率和噪声功率的式子


C的式子是使用下面两个式子得出

为什么 max I 等于后面每个I分量的求和解释如下，如果多维连续信道是无记忆的，则存在

关于式子的等式为什么成立

• 第一个等号：之前提到过，在加性连续信道中，信道的传递概率密度函数就等于噪声的概率密度𝑝(𝑦|𝑥) = 𝑝(𝑛)，进而可证明𝐻(𝑌|𝑋) = 𝐻(𝑁)，说明条件熵𝐻(𝑌|𝑋) 是由于信道中噪声引起的，它完全等于噪声信源的熵，称𝐻(𝑁)为噪声熵
• 第二个等号：此处有两个变量的替换，先解释**H(N)的替换，因为噪声是高斯噪声，在前面介绍噪声信源中推到过式子；H(Y)**的替换因为在噪声信源小节提到了一个定理，若一个连续信源输出信号的平均功率被限定为P，则其输出信号幅度的概率密度分布时高斯分布时，信源有最大的熵，其值为(1/2)𝑙𝑜𝑔2𝜋𝑒P，也就是信源输出是高斯分布时信息熵最大。因此两个替换都是形式一样的log式子。
• 为什么H(Y)的替换中功率为PS+PN：在信道输出信号Y的平均功率限制在P0时，由前已知，若Y是均值为0的高斯变量，其熵h(Y)最大，而输出信号Y是输入信号X和噪声的线性叠加。又已知噪声是均值为0，方差为𝜎2的高斯变量，并与输入信号X彼此独立统计。那么，要使Y是均值0，方差为P0的高斯变量必须要求输入信号也是均值为0，方差为PS=P0-𝜎2的高斯变量（因为从概率论知，统计独立的正态分布的随机变量之和仍是正态分布变量，并且和变量的方差等于各变量的方差之和）

什么是信道无记忆性：若连续信道在任一时刻输出的变量只与对应时刻的输入变量有关，与以前时刻的输入、输出变量无关，也与以后输出变量无关，则此信道为无记忆信道

总结下来示意图如下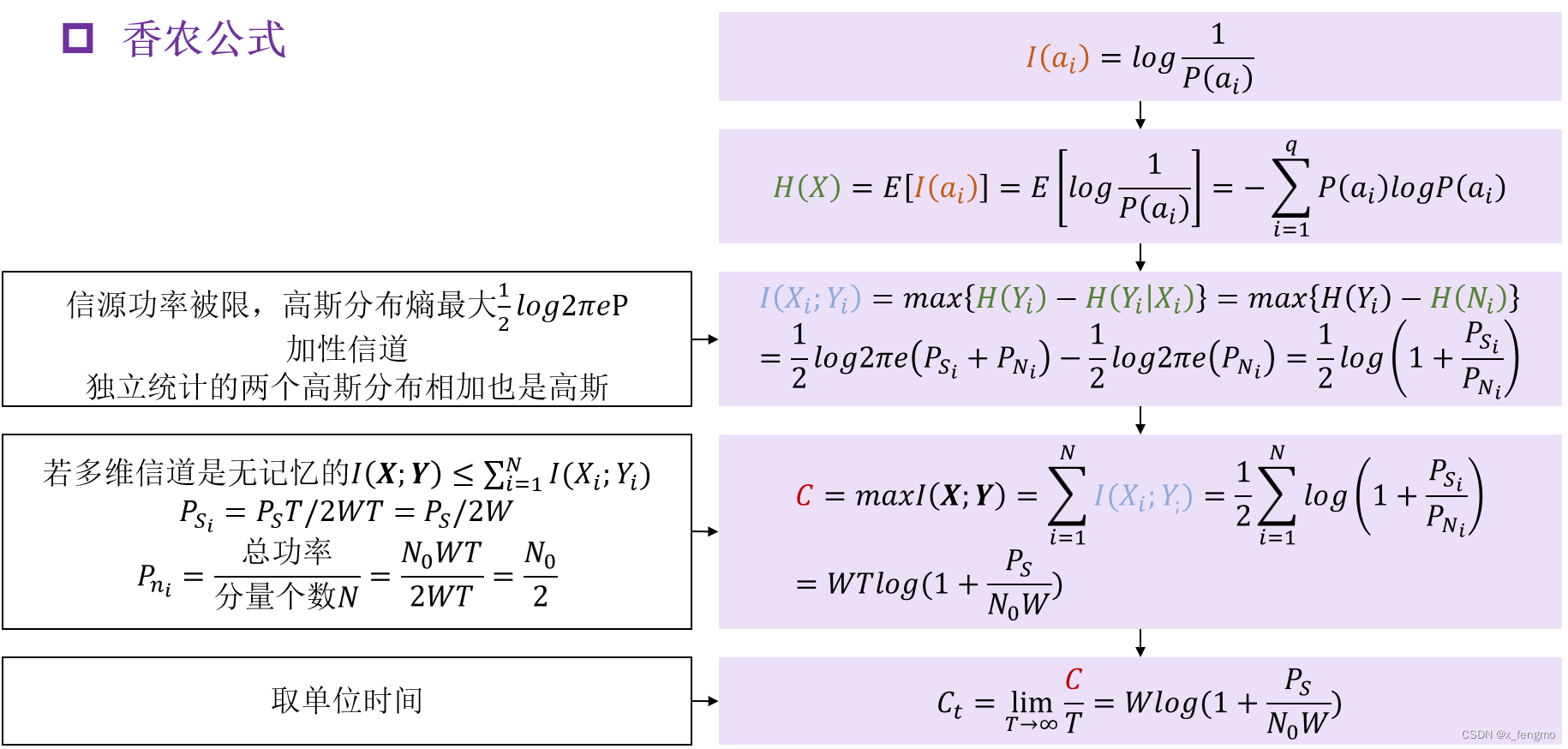

深入浅出学习傅里叶变换，个人评价，真大佬
并且参照《通信原理（第7版）》《信息论——基础理论与应用（第4版）》