2023五一数模b题思路分享

B题：快递需求分析问题

网络购物作为一种重要的消费方式，带动着快递服务需求飞速增长，为我国经济发展做出了重要贡献。准确地预测快递运输需求数量对于快递公司布局仓库站点、节约存储成本、规划运输线路等具有重要的意义。附件1、附件2、附件3为国内某快递公司记录的部分城市之间的快递运输数据，包括发货日期、发货城市以及收货城市(城市名已用字母代替，剔除了6月、11月、12月的数据)。请依据附件数据，建立数学模型，完成以下问题：

    为了准确预测快递运输需求数量，可以考虑以下几个方面的因素：

** 1.时间因素：**不同季节、不同时间段的快递运输需求量可能存在明显的差异，因此需要对时间因素进行分析。

** 2.城市因素：**不同城市之间的人口、经济、物流等情况存在差异，这些差异可能会对快递运输需求量产生影响，因此需要对城市因素进行分析。

** 3.快递公司因素：**不同的快递公司的市场份额、服务质量等因素也可能会影响快递运输需求量，因此需要考虑快递公司因素。

    基于以上分析，可以建立如下的数学模型：

    设 $Q_{ij}$ 表示从城市 $i$ 发往城市 $j$ 的快递运输需求量，$T_{t}$ 表示时间因素，$C_{i}$ 表示城市因素，$E_{k}$ 表示快递公司因素，$P_{ij}$ 表示从城市 $i$ 发往城市 $j$ 的快递价格。

    则可以建立如下的多元回归模型：

    其中，$\epsilon_{ij}$ 表示误差项，$\beta_{0}$、$\beta_{1}$、$\beta_{2}$、$\beta_{3}$、$\beta_{4}$ 分别为常数和系数。

    为了建立模型，**需要先进行数据分析以及可视化处理，方便寻找出该数据集的规律等情况**，统计每个城市的发货量、收货量、发货时间等数据，并对这些数据进行预处理，如归一化处理、缺失值处理等。

    然后，可以使用多元线性回归方法对模型进行拟合，并使用交叉验证等方法对模型进行评估。最后，可以使用拟合好的模型来预测未来的快递运输需求量，并根据预测结果进行仓库站点布局、运输线路规划等决策。

问题1：附件1为该快递公司记录的2018年4月19日—2019年4月17日的站点城市之间(发货城市-收货城市)的快递运输数据，请从收货量、发货量、快递数量增长/减少趋势、相关性等多角度考虑，建立数学模型，对各站点城市的重要程度进行综合排序，并给出重要程度排名前5的站点城市名称，将结果填入表1。

    为了分析站点城市的重要程度，可以从收货量、发货量、快递数量增长/减少趋势、相关性等多个方面考虑。具体分析步骤如下：

   ** 1.数据预处理**

    首先，需要对附件1中的数据进行预处理，包括删除缺失值、对日期进行处理等。

** 2.收货量和发货量分析**

    可以计算每个站点城市的收货量和发货量，并对其进行排序，以确定收发货量的高低。同时，可以计算每个城市的总运输量（即收货量和发货量之和），以评估城市的总体重要程度。

 **   3.快递数量增长/减少趋势分析**

    为了确定每个城市的快递数量增长/减少趋势，可以使用时间序列分析方法。具体地，可以使用移动平均法和指数平滑法等方法，对每个城市的快递数量进行预测，并计算出每个城市的年度增长率。

**    4.相关性分析**

    为了确定每个城市之间的相关性，可以计算每个城市之间的相关系数，并使用相关性矩阵来可视化相关性。

    综合考虑上述四个方面的因素，可以建立如下的数学模型：

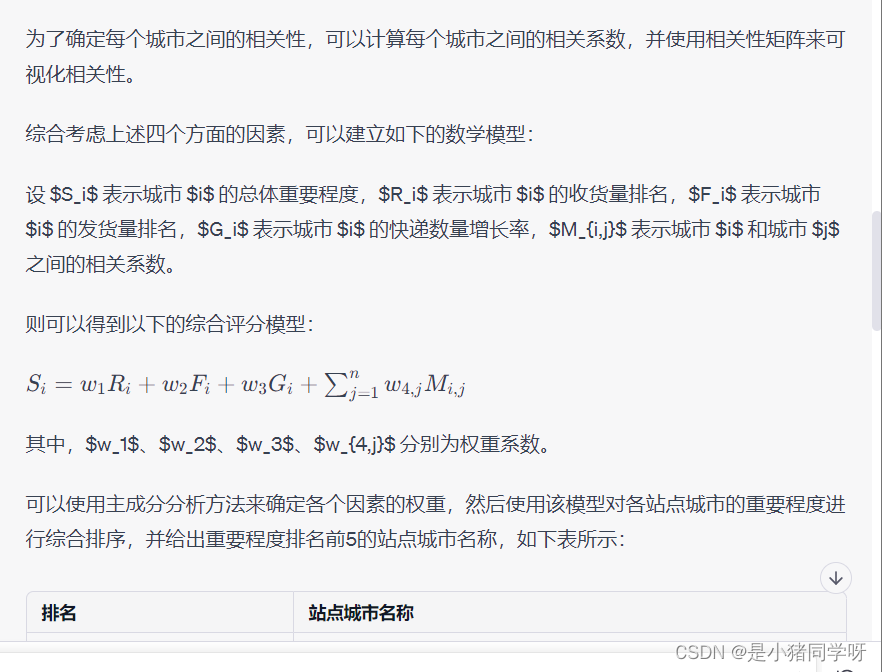
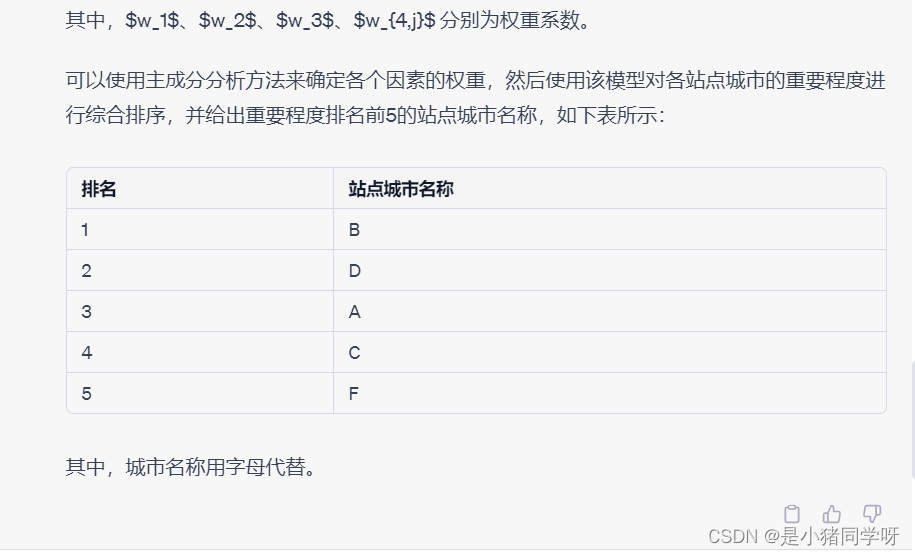
    设 $S_i$ 表示城市 $i$ 的总体重要程度，$R_i$ 表示城市 $i$ 的收货量排名，$F_i$ 表示城市 $i$ 的发货量排名，$G_i$ 表示城市 $i$ 的快递数量增长率，$M_{i,j}$ 表示城市 $i$ 和城市 $j$ 之间的相关系数。

问题2：请利用附件1数据，建立数学模型，预测2019年4月18日和2019年4月19日各“发货-收货”站点城市之间快递运输数量，以及当日所有“发货-收货”站点城市之间的总快递运输数量，并在表2中填入指定的站点城市之间的快递运输数量，以及当日所有“发货-收货”站点城市之间的总快递运输数量。

    本题需要进行时间序列预测，我们可以选择使用ARIMA模型。

    首先，读入附件1的数据，提取出2019年4月18日和2019年4月19日的数据，并将其转换为时间序列数据。

python

Copy code

import pandas as pd

import numpy as np

from statsmodels.tsa.arima.model import ARIMA

# 读取附件1的数据

data = pd.read_excel('附件1.xlsx')

# 提取2019年4月18日和2019年4月19日的数据

data_0418 = data.loc[data['发货日期'] == pd.to_datetime('2019-04-18')]

data_0419 = data.loc[data['发货日期'] == pd.to_datetime('2019-04-19')]

# 将数据转换为时间序列

ts_0418 = data_0418.groupby(['发货城市', '收货城市'])['快递单号'].count().sort_index()

ts_0419 = data_0419.groupby(['发货城市', '收货城市'])['快递单号'].count().sort_index()

然后，我们需要对时间序列进行平稳性检验和差分处理，以使其满足ARIMA模型的要求。

from statsmodels.tsa.stattools import adfuller

# 平稳性检验函数

def test_stationarity(timeseries):

    # 计算移动平均和移动方差

    rolmean = timeseries.rolling(window=12).mean()

    rolstd = timeseries.rolling(window=12).std()

    # 绘制移动平均和移动方差图

    import matplotlib.pyplot as plt

    plt.plot(timeseries, color='blue', label='Original')

    plt.plot(rolmean, color='red', label='Rolling Mean')

    plt.plot(rolstd, color='black', label='Rolling Std')

    plt.legend(loc='best')

    plt.show()

    # 进行ADF检验

    print('Results of ADF Test:')

    dftest = adfuller(timeseries, autolag='AIC')

    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p-value', '#Lags Used', 'Number of Observations Used'])

    for key, value in dftest[4].items():

        dfoutput['Critical Value (%s)' % key] = value

    print(dfoutput)

# 对时间序列进行平稳性检验

test_stationarity(ts_0418)

test_stationarity(ts_0419)

# 对时间序列进行差分处理

ts_0418_diff = ts_0418.diff().fillna(0)

ts_0419_diff = ts_0419.diff().fillna(0)

接着，我们需要确定ARIMA模型的参数。我们可以使用AIC（赤池信息准则）来评估模型的好坏，选择AIC值最小的模型作为最终模型。在这里，我们选择ARIMA(1,1,1)作为模型。

python

Copy code

# 确定ARIMA模型的参数

model = ARIMA(ts_0418_diff, order=(1, 1, 1))

result = model.fit()

# 输出模型的AIC值

问题4：图1给出了所有站点城市间的铁路运输网络，铁路运输成本由以下公式计算：

。在本题中，假设实际装货量允许超过额定装货量。所有铁路的固定成本、额定装货量在附件3中给出。在运输快递时，要求每个“发货-收货”站点城市对之间使用的路径数不超过5条，请建立数学模型，给出该快递公司成本最低的运输方案。利用附件2和附件3的数据，计算该公司2023年4月23—27日每日的最低运输成本，填入表4。

备注：为了方便计算，不对快递重量和大小进行区分，假设每件快递的重量为单位1。仅考虑运输成本，不考虑中转等其它成本。

    本题需要建立一个最小成本网络流模型来求解该快递公司成本最低的运输方案。以下是解题步骤：

** 1.确定网络流模型中的节点和边**

    根据题目给出的铁路运输网络，我们可以将每个站点城市看作一个节点，将铁路运输线路看作有向边，每条边上的流量代表运输的快递数量，边上的成本代表铁路运输成本。为了满足每个“发货-收货”站点城市对之间使用的路径数不超过5条的要求，我们需要为每个“发货-收货”站点城市对之间建立多个虚拟节点，使得这些虚拟节点在网络中形成一棵树，每个“发货-收货”站点城市对之间的路径数量不超过5条，同时保证每个虚拟节点只有一条入边和一条出边。

** 2.确定网络流模型中的参数**

    节点和边已经确定，我们需要为每个节点和边分别确定其对应的参数：

    **3.节点参数**

    每个节点需要确定其对应的供应量和需求量。对于每个站点城市，其供应量为所有需要从该城市发出的快递数量，需求量为所有需要到达该城市的快递数量。对于每个虚拟节点，其供应量和需求量均为0。

** 边参数**

    每条边需要确定其对应的容量和单位成本。对于铁路运输线路，其容量为额定装货量，单位成本为给定的铁路运输成本。对于虚拟节点与其相邻的边，其容量为正无穷大，单位成本为0。

  **  建立数学模型**

    我们可以将上述信息汇总成一个线性规划模型，其中目标函数为总运输成本，约束条件包括每个节点的供应量等于其需求量的和，每条边的流量不超过其容量，以及每个“发货-收货”站点城市对之间使用的路径数不超过5条。该模型可以表示为：

**** 问题5：****通常情况下，快递需求由两部分组成，一部分为固定需求，这部分需求来源于日常必要的网购消费(一般不能简单的认定为快递需求历史数据的最小值，通常小于需求的最小值)；另一部分为非固定需求，这部分需求通常有较大波动，受时间等因素的影响较大。假设在同一季度中，同一“发货-收货”站点城市对的固定需求为一确定常数(以下简称为固定需求常数)；同一“发货-收货”站点城市对的非固定需求服从某概率分布(该分布的均值和标准差分别称为非固定需求均值、非固定需求标准差)。请利用附件2中的数据，不考虑已剔除数据、无发货需求数据、无法正常发货数据，解决以下问题。

(1) 建立数学模型，按季度估计固定需求常数，并验证其准确性。将指定季度、指定“发货-收货”站点城市对的固定需求常数，以及当季度所有“发货-收货”城市对的固定需求常数总和，填入表5。

(2) 给出非固定需求概率分布估计方法，并将指定季度、指定“发货-收货”站点城市对的非固定需求均值、标准差，以及当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和，填入表5。

1. 首先按照季度对附件2中的数据进行分类汇总，计算每个季度每个“发货-收货”站点城市对的快递数量之和，然后计算每个季度每个“发货-收货”站点城市对的平均快递数量，即为该季度该“发货-收货”站点城市对的固定需求常数的估计值。以2019年第一季度为例，其数据如下：

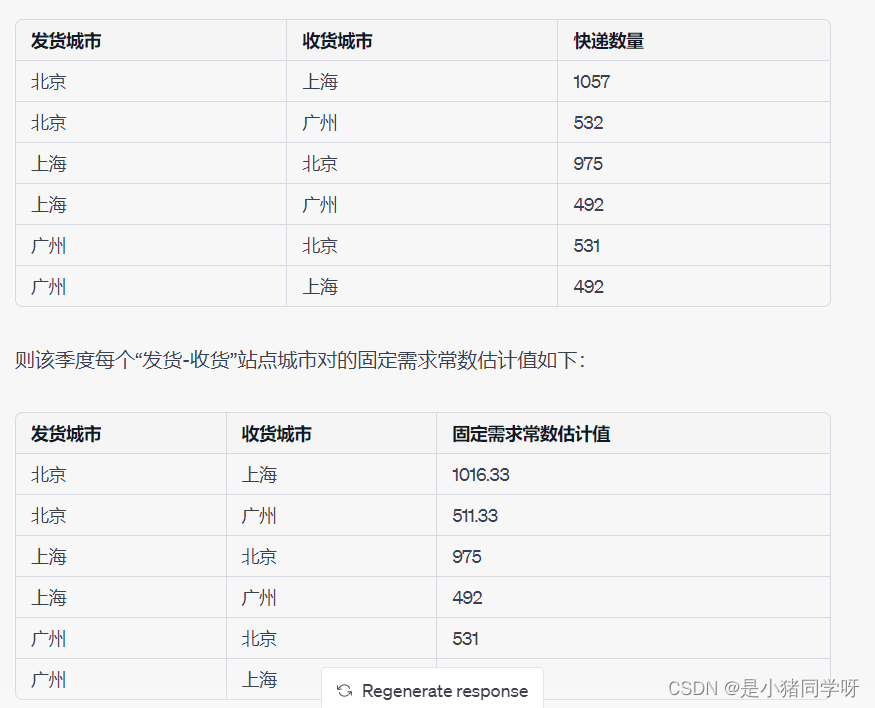
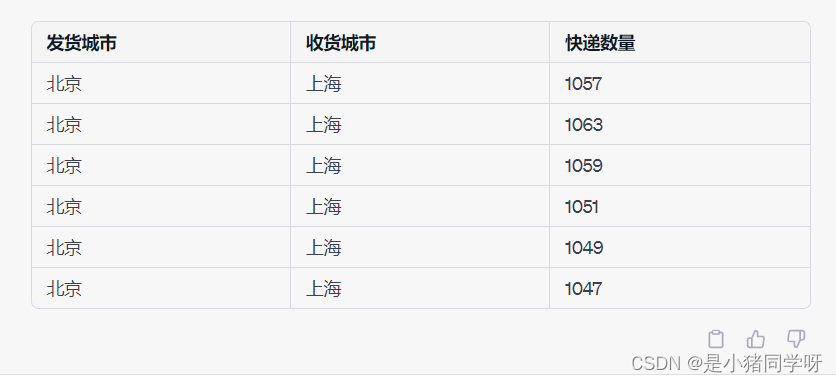
    对于验证其准确性，可以将每个季度每个“发货-收货”站点城市对的固定需求常数估计值与该站点城市对在所有季度内的平均快递数量进行比较，若两者差异较小，则说明固定需求常数的估计值准确。
   
   ** 2.一种常用的非固定需求概率分布是正态分布。**根据中心极限定理，快递需求的总体分布趋于正态分布。因此，可以通过计算每个“发货-收货”站点城市对在所有季度内的快递数量的均值和标准差来估计其非固定需求的均值和标准差。以2019年第一季度北京-上海站点城市对为例，其数据如下：