二分类及多分类ROC和PR曲线绘制

目录

   前两天2022年**第二届全国高校大数据竞赛**已经落下帷幕，比赛中也用到了一些分类预测模型，同时也要对这些模型的性能进行评估，那么肯定就少不了ROC曲线以及PR曲线，下面就比赛过程中用到的一些模型及相应的曲线绘制做一个简单的总结。

1.二分类曲线

在绘制曲线之前，首先来看一下混淆矩阵。

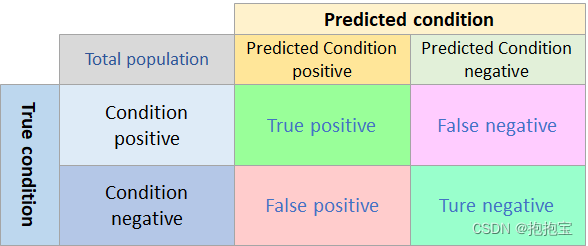
其中TP(True positive)为真正类，即真实值是正类，预测值也是正类的样本；FN(False negative)为假负类，即真实值是正类，预测值是负类的样本；FP(False positive)为假正类，即真实值是负类，预测值是正类的样本；TN(True negative)为真负类，即真实值是负类，预测值也是负类的样本。

本文中二分类曲线是将四种模型的曲线绘制在一起进行对比，观察模型性能差异。

1.1 二分类ROC曲线

#绘制ROC曲线
probas_dtc=dtc.predict_proba(x_test)#决策树
probas_rfc=rfc.predict_proba(x_test)#随机森林
probas_gbc=gbc.predict_proba(x_test)#梯度提升树
probas_xgbc=xgbc.predict_proba(x_test)#XGBoost
fpr_dtc,tpr_dtc,thresholds_dtc=roc_curve(y_test,probas_dtc[:,1])
fpr_rfc,tpr_rfc,thresholds_rfc=roc_curve(y_test,probas_rfc[:,1])
fpr_gbc,tpr_gbc,thresholds_gbc=roc_curve(y_test,probas_gbc[:,1])
fpr_xgbc,tpr_xgbc,thresholds_xgbc=roc_curve(y_test,probas_xgbc[:,1])
dtc_auc=auc(fpr_dtc,tpr_dtc)
rfc_auc=auc(fpr_rfc,tpr_rfc)
gbc_auc=auc(fpr_gbc,tpr_gbc)
xgbc_auc=auc(fpr_xgbc,tpr_xgbc)
plt.rcParams['font.family']=['Times New Roman']
plt.rcParams['figure.figsize']=(8,6)
plt.plot(fpr_dtc,tpr_dtc,color='k',label='dtc_AUC=%0.3f'%dtc_auc)
plt.plot(fpr_rfc,tpr_rfc,color='b',label='rfc_AUC=%0.3f'%rfc_auc)
plt.plot(fpr_gbc,tpr_gbc,color='g',label='gbc_AUC=%0.3f'%gbc_auc)
plt.plot(fpr_xgbc,tpr_xgbc,color='y',label='xgbc_AUC=%0.3f'%xgbc_auc)
plt.title('Receiver Operating Characteristic')
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.05,1.05])
plt.ylim([-0.05,1.05])
plt.ylabel('True positive Rate')
plt.xlabel('False positive Rate')
plt.grid(linestyle='-.')  
plt.grid(True)
plt.show()

4种模型的ROC曲线：

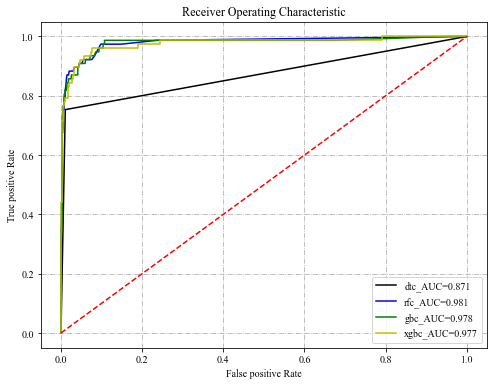
其中，横坐标为假正率（FPR），即预测为正例但实际为负例的样本占所有负例样本的比例；纵坐标为真正率（TPR），即预测为正例且实际为正例的样本占所有正例样本的比例。计算公式分别如下：

在ROC曲线中，模型的曲线越靠近左上角说明该模型的性能越好，如果曲线发生交叉不太好判断时，可以通过曲线与下方坐标轴围成的面积大小即AUC值来判断，一般曲线都是在对角线的上方，因此AUC的值一般在0.5到1之间，AUC值越大，说明该曲线性能越好。

1.2 二分类PR曲线

#绘制PR曲线
probas_dtc=dtc.predict_proba(x_test)#决策树
probas_rfc=rfc.predict_proba(x_test)#随机森林
probas_gbc=gbc.predict_proba(x_test)#梯度提升树
probas_xgbc=xgbc.predict_proba(x_test)#XGBoost
precision_dtc,recall_dtc,thresholds_dtc=precision_recall_curve(y_test,probas_dtc[:,1])
precision_rfc,recall_rfc,thresholds_rfc=precision_recall_curve(y_test,probas_rfc[:,1])
precision_gbc,recall_gbc,thresholds_gbc=precision_recall_curve(y_test,probas_gbc[:,1])
precisione_xgbc,recall_xgbc,thresholds_xgbc=precision_recall_curve(y_test,probas_xgbc[:,1])
plt.rcParams['font.family']=['Times New Roman']
plt.rcParams['figure.figsize']=(8,6)
plt.plot(precision_dtc,recall_dtc,color='k',label='DecisionTreeClassifier')
plt.plot(precision_rfc,recall_rfc,color='b',label='RandomForestClassifier')
plt.plot(precision_gbc,recall_gbc,color='g',label='GradientBoostingClassifier')
plt.plot(precisione_xgbc,recall_xgbc,color='y',label='XGBoost')
plt.title('Precision-recall curve')
plt.legend(loc='lower left')
plt.plot([1,0],[0,1],'r--')
plt.xlim([-0.05,1.05])
plt.ylim([-0.05,1.05])
plt.ylabel('Precision')
plt.xlabel('Recall')
plt.grid(linestyle='-.')  
plt.grid(True)
plt.show()

4种模型的PR曲线：

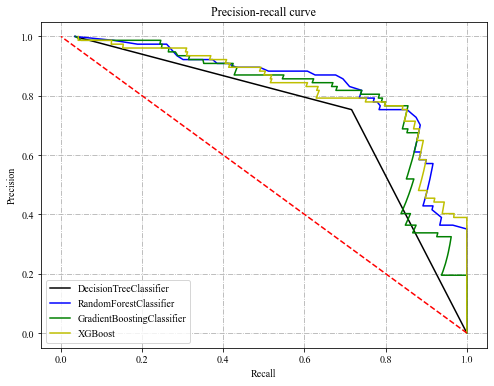
其中，横坐标为召回率（Recall），纵坐标为**准确率(Precision)**， 计算公式分别如下：

PR曲线代表的是准确率和召回率的关系，曲线越靠近右上角则说明模型训练效果越好。如果曲线发生交叉不太好判断，可以再根据模型的F1得分判断模型性能的好坏，其计算公式如下：

2.多分类曲线

对于多分类曲线，这里是根据模型准确性得分选取得分最高的模型，然后绘制其每一个类别的曲线。

在绘制多分类曲线之前，首先要对数据类别进行编码操作，然后构建模型进行训练。

#编码
from sklearn.preprocessing import label_binarize
y_test1=label_binarize(y_test,classes=[1,2,3,4,5])
n_classes=y_test1.shape[1]
#训练模型
from sklearn.multiclass import OneVsRestClassifier
rfc1=OneVsRestClassifier(DecisionTreeClassifier())
clf=xgbc.fit(x_train,y_train)
y_prob=clf.predict_proba(x_test)

2.1多分类ROC曲线

#绘制多分类ROC曲线
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test1[:, i], y_prob[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])
plt.rcParams['font.family']=['Times New Roman']
plt.figure()
lw = 1
colors = ['blue', 'red', 'green', 'black', 'yellow']
for i, color in zip(range(n_classes), colors):
    plt.plot(fpr[i], tpr[i], color=color, lw=lw,
             label='ROC curve of class {0} (AUC = {1:0.3f})'
             ''.format(i+1, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([-0.05, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic for multi-class data')
plt.legend(loc="lower right")
plt.show()

XGBoost模型5种类型的ROC曲线：

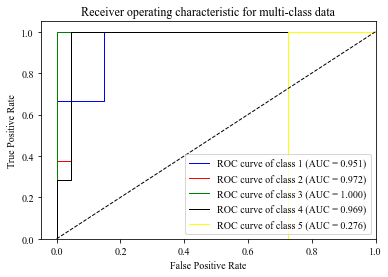
这里比较的是五个列表的分类好坏，可以看出第3类的分类效果是最好的；第五类的曲线在对角线下方是由于样本数量太少，导致分类准确性不高。

2.2 多分类PR曲线

#绘制多分类PR曲线
precision = dict()
recall = dict()
for i in range(n_classes):
    precision[i], recall[i], _ = precision_recall_curve(y_test1[:, i], y_prob[:, i])
plt.rcParams['font.family']=['Times New Roman']
plt.figure()
lw = 1
colors = ['blue', 'red', 'green', 'black', 'yellow']
for i, color in zip(range(n_classes), colors):
    plt.plot(precision[i], recall[i], color=color, lw=lw+0.5,
             label='PR curve of class {0}'.format(i+1))
plt.plot([1, 0], [0, 1], 'k--', lw=lw)
plt.xlim([-0.05, 1.05])
plt.ylim([0, 1])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Precision recall curve for multi-class data')
plt.legend(loc="lower left")
plt.show()

XGBoost 模型5种分类的PR曲线：

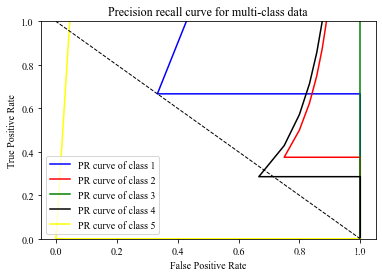
将PR曲线与ROC曲线对比，多分类情况下还是用ROC曲线进行判断比较合适，PR曲线明显不如ROC曲线那么好看，另一个原因也是由于样本数量比较少，在样本数量比较多的情况下，使用PR曲线还是比较不错的。

好啦，总结就到这里！也希望参加比赛的小伙伴可以取得好成绩哦！