统计信号处理-使用维纳滤波和逆滤波对图像进行恢复-matlab仿真-附代码

1. 使用维纳滤波对噪声图像恢复

2. 题目及滤波图像恢复简介

3. 题目

将维纳滤波应用于图像恢复，假设退化图像为一加性高斯白噪声污染的图像，试用逆滤波方法和维纳滤波方法恢复图像，并比较其效果；查阅文献，尝试使用迭代维纳滤波的方法进一步提高效果，注意构建正确的修正项。

1. 逆滤波用于图像恢复简介

逆滤波法是一种从添加了噪声的图像中恢复原始图像的技术，它的基本思想是使用滤波器和滤波器的逆滤波器。在这种方法中，首先用一个适当的滤波器（如维纳滤波器）对污染图像进行滤波，然后再使用该滤波器的逆滤波器对滤波后的图像进行滤波，从而恢复出原始图像。由于在滤波器的逆滤波器中，噪声的影响会被抵消，因此可以有效地恢复原始图像。

1. 维纳滤波用于图像恢复简介

维纳滤波是一种基于信号模型的迭代滤波算法，它假设信号为有噪声的线性系统动态响应和加性高斯噪声的组合。维纳滤波的基本思想是，首先估计信号和噪声的模型参数，然后根据模型参数来构造滤波器，最后使用滤波器消除噪声。

维纳滤波可以对噪声图像进行恢复，因为它可以根据信号和噪声的模型参数构造滤波器，然后通过滤波器消除噪声，从而恢复噪声图像。

1. 逆滤波与维纳滤波的原理

2. 逆滤波的原理

一般来说，图像的退化模型可以表示为

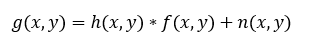
其中，g(x,y) 表示退化后的图像，h(x,y)为点扩散函数，f(x,y) 为原始图像，n(x,y) 为引入的噪声。在频域上面可以表示为

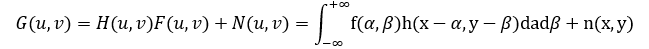
将其变换到频域可以得到

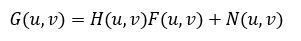
所以

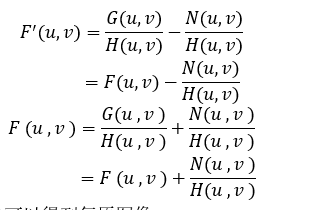
将其进行傅里叶反变换可以得到复原图像。

1. 维纳滤波的原理

维纳滤波是另外一种比较常见的图像复原方法，计算复杂度相对较小并且考虑了噪声的影响。通常情况下，假设图像和噪声是相互独立的且至少存在一个均值为零，恢复图像和模糊图像两者的灰度级呈线性关系时，维纳滤波可表示为

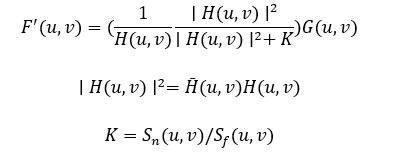
其中，Sn(u,v)为噪声功率谱，Sf(u,v)为原图像功率谱。

1. Matlab仿真结果

2. 逆滤波仿真结果

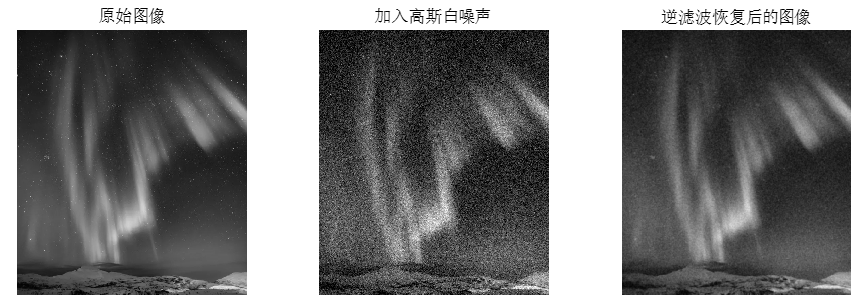
由上图可见，原始图像是一幅极光景色且无肉眼可见噪声，经过加入高斯白噪声后，图像中出现了随机位置的细小的白点，经过逆滤波恢复后，图像中的噪点明显减少，但同时也会过滤掉原始图像的与噪点类似的星星。

1. 维纳滤波仿真结果

经过维纳滤波恢复后，图像中的噪点明显减少，但是与逆滤波不同，维纳滤波后的图像中的星星并没有被认为是噪点而完全滤除。

1. 迭代维纳滤波仿真结果

如上图所示，迭代维纳滤波对于图像恢复有着很好的效果，能够滤除大部分的噪点。经过数次迭代后，图像已经恢复的很好。迭代次数达到一定上限后，效果则变化不明显。

代码

% Load image
img = imread('C:\Users\songy\OneDrive\Pictures\sample.png');
% Convert to grayscale
img_gray = rgb2gray(img);
% Add Gaussian white noise
noisy_img = imnoise(img_gray, 'gaussian', 0, 0.01);
% Perform Wiener filtering
filtered_img = wiener2(noisy_img, [5 5]);
% Display the filtered image
subplot(1,3,1)
imshow(img_gray)
title('原图')
subplot(1,3,2)
imshow(noisy_img)
title('加入高斯白噪声的图像')
subplot(1,3,3)
imshow(filtered_img)
title('维纳滤波后的图像')

%迭代部分，单独执行
img1=wiener2(noisy_img, [5 5]);
img2=wiener2(img1, [5 5]);
img3=wiener2(img2, [5 5]);
img4=wiener2(img3, [5 5]);
subplot(2,2,1)
imshow(noisy_img)
title('带噪声图')
subplot(2,2,2)
imshow(img1)
title('第一次迭代')
subplot(2,2,3)
imshow(img2)
title('第二次迭代')
subplot(2,2,4)
imshow(img3)
title('第三次迭代')
%% 加载图像
I=imread('C:\Users\songy\OneDrive\Pictures\sample.png');
%% 生成维纳滤波器
% Convert to grayscale
img_gray = rgb2gray(I);
% Add Gaussian white noise
noisy_img = imnoise(img_gray, 'gaussian', 0, 0.01);
N=5; % 维纳滤波器大小
sigma=2; % 标准差
h=fspecial('gaussian',N,sigma);
%% 逆滤波处理
J=imfilter(noisy_img,h,'symmetric');
%% 显示结果
figure;
subplot(1,3,1);
imshow(img_gray);
title('原始图像');
subplot(1,3,2);
imshow(noisy_img);
title('加入高斯白噪声');
subplot(1,3,3);
imshow(J);
title('逆滤波恢复后的图像');