数学建模常用算法—马尔可夫预测

今天数模君带大家学习一下数学建模中的预测算法之马尔科夫预测。

模型的含义

马尔可夫（Markov)预测法，就是一种关于事件发生的概率预测方法。它是根据事件的目前状况来预测其将来各个时刻（或时期)变动状况的一种预测方法。马尔可夫预测法是地理预测研究中重要的预测方法之一。

1. 状态

指某一件事在某个时刻（或时期）出现的某种结果。

2.状态转移过程

事件的发展，从一种状态转变为另一种状态，称为状态转移。

3.马尔可夫过程

在事件的发展过程中，若每次状态的转移都仅与前一时刻的状态有关，而与过去的状态无关，或者说状态转移过程是无后效性的，则这样的状态转移过程就称为马尔可夫过程。

4.状态转移概率

用于描述，在事件的发展变化过程中，从某一种状态出发，在下一时刻转移到其它状态的可能性大小。

为了求出每一个，一般采用频率近似概率的思想进行计算。

5.状态转移概率矩阵

假定某一个事件的发展过程有n个可能的状态，即E1，E2，…，En。记为从状态Ei转变为状态Ej的状态转移概率

则矩阵

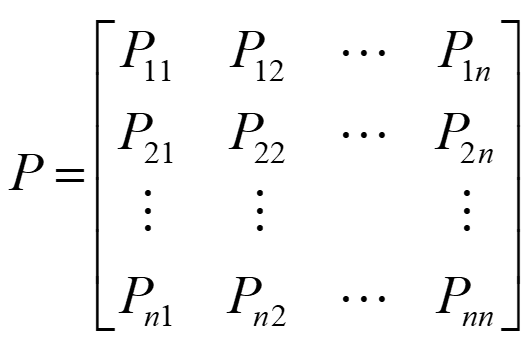
实例分析

题1：考虑某地区农业收成变化的3个状态，即“丰收”、“平收”和“歉收”。记E1为“丰收”状态，E2为“平收”状态，E3为“歉收”状态。表给出了该地区1975—2014年期间农业收成的状态变化情况。试计算该地区农业收成变化的状态转移概率矩阵。

将例题1中2014年的农业收成状态记为 =[0,1, 0] （因为2014年处于“平收”状态），将状态转移概率矩阵代入递推公式，求2015—2025年可能出现的各种状态的概率。

> library(markovchain)
> library(readxl)
> library(tidyverse)
> library(expm)
> library(diagram)
> setwd("D:/code")
> tb456=read_xlsx('markov.xlsx') %>%
+   mutate(state1=lag(state)) 
>  #交叉统计，变量state1转为state的个数
>  tss= table(tb456[-1,]$state1,tb456[-1,]$state) 
> #返回交叉表的频率,即状态转移概率矩阵
> tmA=prop.table(tss,1) 
> tmA

            E1        E2        E3
  E1 0.2000000 0.4666667 0.3333333
  E2 0.5384615 0.1538462 0.3076923
  E3 0.3636364 0.4545455 0.1818182

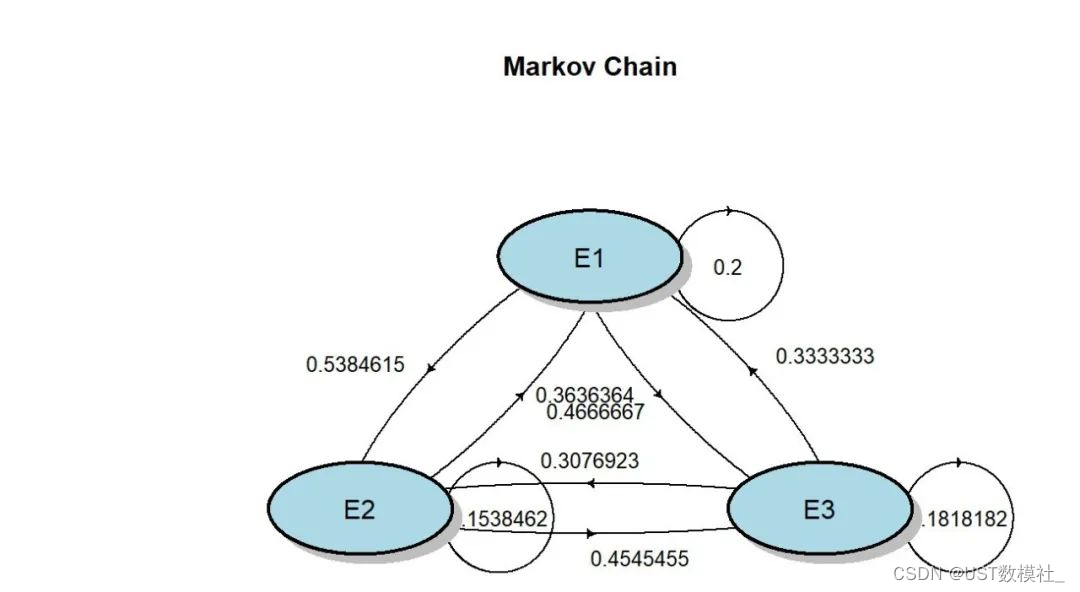
> #可视化
> plotmat(tmA,pos = c(1,2), 
+         lwd = 1, box.lwd = 2, 
+         cex.txt = 0.8, 
+         box.size = 0.1, 
+         box.type = "circle", 
+         box.prop = 0.5,
+         box.col = "light blue",
+         arr.length=.1,
+         arr.width=.1,
+         self.cex = .6,
+         self.shifty = -.01,
+         self.shiftx = .15,
+         main = "Markov Chain")

> #初始状态
> inital=matrix(c(0,1,0),nrow=1, byrow=TRUE)
> #预测下一年
> fc15=inital %*% tmA
> #预测下两年
> fc16=inital %*% tmA%*% tmA
> #预测第三年，tmA%^% 3相当于tmA%*% tmA%*%tmA
> fc17=inital %*% (tmA%^% 3)
> #要进行多年预测，因此编写一个函数
> myfunction=function(n){
+   inital %*% (tmA%^% n)
+ }
> mats=matrix(data = NA,nrow = 11,ncol = 3) %>% 
+ data.frame()
> #预测2015-2025年，共11年，用一个dataframe来进行结果存储
> for (i in 1:11) {
+   mats[i,]=myfunction(i)
+ }
> mats$year=seq(2015,2025)
> colnames(mats)=c('E1','E2',"E3",'year')
> mats

     E1        E2        E3 year
1  0.5384615 0.1538462 0.3076923 2015
2  0.3024207 0.4148108 0.2827685 2016
3  0.3866687 0.3334778 0.2798534 2017
4  0.3586636 0.3589558 0.2823806 2018
5  0.3677005 0.3509551 0.2813444 2019
6  0.3648230 0.3534705 0.2817065 2020
7  0.3657336 0.3526792 0.2815872 2021
8  0.3654463 0.3529282 0.2816256 2022
9  0.3655368 0.3528498 0.2816134 2023
10 0.3655083 0.3528745 0.2816172 2024
11 0.3655173 0.3528667 0.2816160 2025

> #-------利用markovchain包中的函数快速实现-------------
> #返回概率转移矩阵
> Ma=createSequenceMatrix(tb456$state,toRowProbs = T)
> #定义一个markov对象
> dtmcA <- new("markovchain",transitionMatrix=Ma,
+              states=c('E1','E2',"E3"),
+              name="MarkovChain A") 
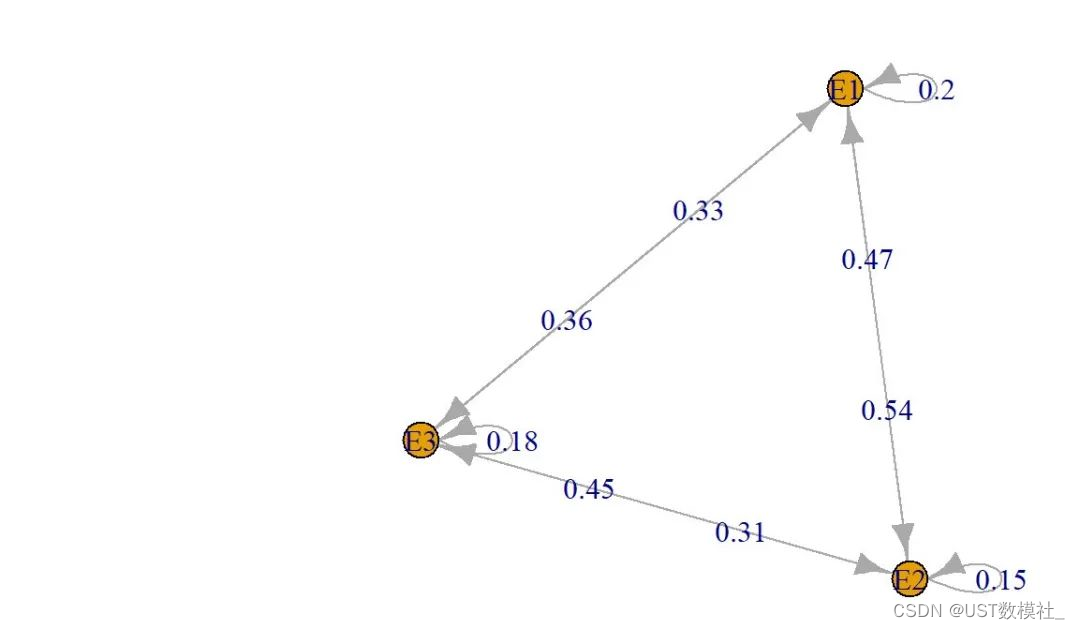
> #可视化
> plot(dtmcA)

> #定义一个dataframe存储结果，结果与mats相同
> mats1=matrix(data = NA,nrow = 11,ncol = 3) %>% 
+   data.frame()
> 
> for (i in 1:11) {
+   mats1[i,]=inital*(dtmcA^i)
+ }
> #终极状态概率
> steadyStates(dtmcA)

最终结果：

 E1        E2        E3
[1,] 0.3655151 0.3528686 0.2816163