题目
- Physics-Informed Geometry-Adaptive Convolutional Neural Networks for Solving Parametric PDEs on Irregular Domai
作者
- Han Gao a,b , Luning Suna,b , Jian-Xun Wanga,b
- a Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN
- b Center for Informatics and Computational Science, University of Notre Dame, Notre Dame, IN
期刊会议
- 在review
年份
- 2020
1 动机与研究内容
- 最近PINN被用作微分方程求解得到了广泛关注,但使用的是fully-connected neural network 网络,而CNN在机器学习中应用广泛,因为CNN的参数共享特性使得对于大尺度时空场的问题能够进行高效的学习
- 但是,CNN最大挑战是只能处理具有类似图像格式的规则几何图形(例如,具有统一网格的矩形域)
- 在这篇文中提出a novel physics-constrained CNN learning architecture, 目的研究不规则区域上无标记数据参数偏微分方程的解,引入椭圆坐标映射,实现了不规则物理域和规则参考域之间的坐标转换
2 问题背景
2.1 Physics-informed convolutional neural networks
- 尽管FC-NN取得了some sucess,但是FC-NN存在scalability issues,这是由于FC-NN的训练cost随着问腿复杂而增加的,特别是在参数变化的情况下,因为PDE残差需要在高维输入空间的大量配置点上进行评估
- 为了有效学习large-scale spatiotemporal solution fields ,卷积网络(CNN)结构在SciML community得到了越来越多的关注。相比于FC-NN,因为通过基于滤波器的卷积操作实现了参数共享,CNNs通常需要的参数少量几个数量集(orders of magnitude fewer parameters ),所以CNN适合处理large-scale and high-dimensional problem
- 将物理信息加到CNN中,
- 可以附加函数到CNN中
- 物理知识可以作为penalty加到损失函数中
- Long等人[66,67]利用深度神经网络和符号网络结合,通过解释学习滤波器从时空数据中发现偏微分方程
- Rackauckas等人[69]开发了通用微分方程(UDEs),利用CNN从数据中发现未知方程
- Singh等人[68]提出了一种低权重可解释卷积编码器-解码器网络,用于捕获各种PDE系统观测数据的不变结构。
- 现有的所有物理信息cnn的研究都只能处理定义在均匀网格的规则(矩形)区域上的问题,不适用于几何形状通常是复杂和不规则的,这是由于CNN提出用于图像,通常是作为欧几里得空间的函数,在一个均匀网格中sample。但是,用于求解不规则域问题的坐标系具有非欧几里得结构,其中:移位不变性证明使用经典卷积滤波器不再有效,基于有限差分,通过卷积运算计算偏导损耗的导数项,这种方法只适用于像矩形区域。
3 本文方法
为了解决非欧几里得结构 ,利用图论、谱变换、嵌入流形等重新构造非欧几里得卷积运,算新提出的几何网络神经网络很难在不同的拓扑中进行推广,而且,如何构造基于pde的损失函数和为物理约束学习设置边界条件也不清楚
- 本文提出一种a novel physics-constrained deep learning method,叫做physics-informed geometry-adaptive convolutional neural network (physics-informed geometry-adaptive convolutional neural network ),目的是在不使用任何标记数据的情况下学习不规则区域上参数偏微分方程的解(训练不需要模拟数据)
主要contribution:
- 提出了一种基于物理的CNN架构,使参数偏微分方程具有不规则几何图形的无数据学习成为可能(对椭圆坐标变换进行了编码,以处理非均匀网格和不规则几何图形);
- 以一种hard manner将边界条件编码到CNN架构中;
- 对参数热方程和Navier-Stokes方程进行了验证;
- 所提出的方法与基于物理的FC-NNs(即PINN)进行精度和效率的比较。此外,据作者所知,这是第一次尝试使用CNN来学习复杂几何上的参数Navier{Stokes方程,而不依赖任何标记数据进行训练
3.1. Physics-constrained learning with classic convolutional neural network(现有经典Physics-constrained CNN)
F
(
u
,
∇
u
,
∇
2
u
,
⋯
;
μ
)
=
0
,
in
Ω
p
B
(
u
,
∇
u
,
∇
2
u
,
⋯
;
μ
)
=
0
,
on
∂
Ω
p
\begin{array}{c} \mathcal{F}\left(\mathbf{u}, \nabla \mathbf{u}, \nabla^{2} \mathbf{u}, \cdots ; \boldsymbol{\mu}\right)=0, \quad \text { in } \Omega_{p} \\ \mathcal{B}\left(\mathbf{u}, \nabla \mathbf{u}, \nabla^{2} \mathbf{u}, \cdots ; \boldsymbol{\mu}\right)=0, \text { on } \partial \Omega_{p} \end{array}
F(u,∇u,∇2u,⋯;μ)=0, in ΩpB(u,∇u,∇2u,⋯;μ)=0, on ∂Ωp(1)
离散解可以通过CNN model估计
u
(
χ
,
μ
(
χ
)
)
≈
u
c
n
n
(
χ
,
μ
(
χ
)
;
Γ
)
\mathbf{u}(\chi, \boldsymbol{\mu}(\boldsymbol{\chi})) \approx \mathbf{u}^{c n n}(\boldsymbol{\chi}, \boldsymbol{\mu}(\boldsymbol{\chi}) ; \Gamma)
u(χ,μ(χ))≈ucnn(χ,μ(χ);Γ) (2)
χ
=
{
x
1
,
⋯
,
x
n
g
}
\chi=\left\{\mathbf{x}_{1}, \cdots, \mathbf{x}_{n_{g}}\right\}
χ={x1,⋯,xng}表示
n
g
n_{g}
ng个固定网格点均匀空间的几何(像像素/体素的图片),
Γ
=
{
γ
l
}
l
=
1
n
l
\Gamma=\left\{\gamma^{l}\right\}_{l=1}^{n_{l}}
Γ={γl}l=1nl组可训练的滤波器,用于卷积操作,输入离散空间轴
χ
\chi
χ以及参数fields
μ
(
χ
)
\mu(\chi)
μ(χ),为了获得输出解,通过应用
Γ
\Gamma
Γ以及非线性算子(如激活函数)作用于输入
g
l
(
x
)
=
ϕ
(
(
g
l
⊙
γ
l
)
(
x
)
)
,
x
∈
χ
l
g^{l}(\mathbf{x})=\phi\left(\left(g^{l} \odot \gamma^{l}\right)(\mathbf{x})\right), \mathbf{x} \in \chi^{l}
gl(x)=ϕ((gl⊙γl)(x)),x∈χl
其中,
⊙
\odot
⊙表示卷积算子
(
g
⊙
γ
)
(
x
)
=
∫
χ
g
(
x
−
x
′
)
γ
(
x
′
)
d
x
′
(g \odot \gamma)(\mathbf{x})=\int_{\chi} g\left(\mathbf{x}-\mathbf{x}^{\prime}\right) \gamma\left(\mathbf{x}^{\prime}\right) d \mathbf{x}^{\prime}
(g⊙γ)(x)=∫χg(x−x′)γ(x′)dx′
在训练集
{
μ
i
,
u
i
d
}
i
=
1
n
d
\left\{\boldsymbol{\mu}_{i}, \mathbf{u}_{i}^{d}\right\}_{i=1}^{n_{d}}
{μi,uid}i=1nd上训练的损失函数定义为
min
Γ
∑
i
=
1
n
d
∥
u
c
n
n
(
χ
,
μ
i
;
Γ
)
−
u
i
d
(
χ
)
∥
Ω
p
⏟
data-based loss:
L
d
a
t
a
\min _{\Gamma} \sum_{i=1}^{n_{d}} \underbrace{\left\|\mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right)-\mathbf{u}_{i}^{d}(\boldsymbol{\chi})\right\|_{\Omega_{p}}}_{\text {data-based loss: } \mathcal{L}_{d a t a}}
minΓ∑i=1nddata-based loss: Ldata∥∥ucnn(χ,μi;Γ)−uid(χ)∥∥Ωp
其中,
∥
⋅
∥
Ω
\|\cdot\|_{\Omega}
∥⋅∥Ω表示在空间域
Ω
p
\Omega_{p}
Ωp上的
L
2
L_{2}
L2 norm,这样的方法需要数值模拟或者实验获得数据,太过expensive,考虑使用下列的损失
min
Γ
∑
i
=
1
n
d
∥
F
(
u
c
n
n
(
χ
,
μ
i
;
Γ
)
,
∇
u
c
n
n
(
χ
,
μ
i
;
Γ
)
,
∇
2
u
c
n
n
(
χ
,
μ
i
;
Γ
)
,
⋯
;
μ
i
)
∥
Ω
p
⏟
equation-based loss:
L
p
d
e
s.t.
B
(
u
c
n
n
(
χ
,
μ
i
;
Γ
)
,
∇
u
c
n
n
(
χ
,
μ
i
;
Γ
)
,
∇
2
u
c
n
n
(
χ
,
μ
i
;
Γ
)
,
⋯
;
μ
i
)
=
0
,
on
∂
Ω
p
\begin{array}{l} \min _{\Gamma} \sum_{i=1}^{n_{d}} \underbrace{\left\|\mathcal{F}\left(\mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla \mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla^{2} \mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \cdots ; \boldsymbol{\mu}_{i}\right)\right\|_{\Omega_{p}}}_{\text {equation-based loss: } \mathcal{L}_{p d e}} \\ \text {s.t. } \mathcal{B}\left(\mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla \mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla^{2} \mathbf{u}^{c n n}\left(\boldsymbol{\chi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \cdots ; \boldsymbol{\mu}_{i}\right)=0, \text { on } \partial \Omega_{p} \end{array}
minΓ∑i=1ndequation-based loss: Lpde∥∥F(ucnn(χ,μi;Γ),∇ucnn(χ,μi;Γ),∇2ucnn(χ,μi;Γ),⋯;μi)∥∥Ωps.t. B(ucnn(χ,μi;Γ),∇ucnn(χ,μi;Γ),∇2ucnn(χ,μi;Γ),⋯;μi)=0, on ∂Ωp(6)
在这篇文章中仅仅关注不使用labeled data
Limitation:
- 在eq(2)中要求在矩形域中的均匀网格点,但是在scientific computing and physical modeling applications中求解域是几何不均匀的网格,在这种情况下前面提到的CNN就Physics-constrained learning with classic convolutional neural network不能用了
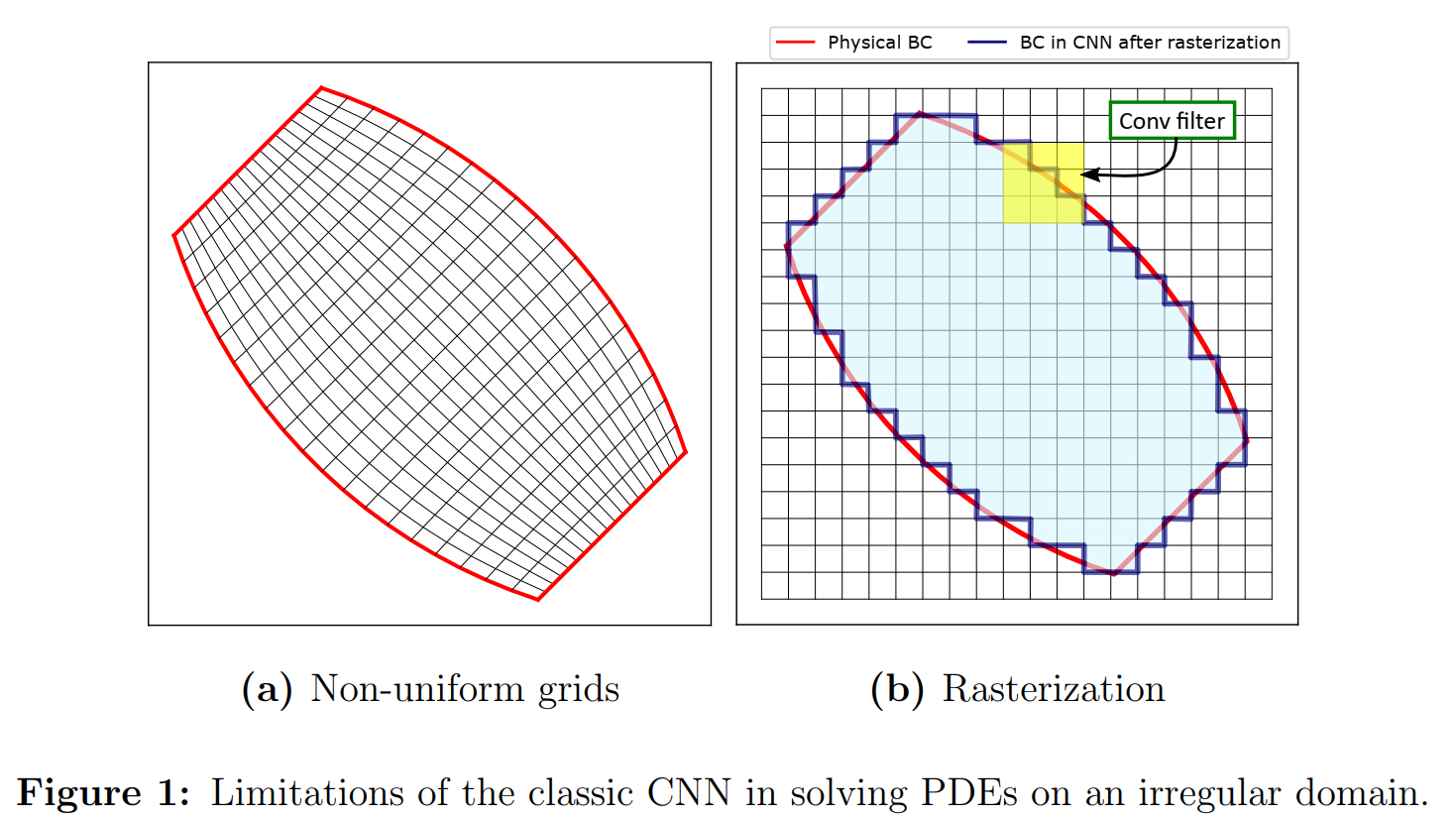
- 光栅(rasterization )如图1右,将不规则区域转化为均匀网格,像素点标记的方法有binaries or Signed Distance Function,但是这样的方法有两点drawbacks
- 光栅化后,边界形状呈阶梯状和锯齿状(图1),在低/中分辨率图像下引入了较大的混叠误差。特别是在边值问题中,即使对边界的一个微小的误表示,也会导致学习解领域中出现较大的误差
- 使用二进制/SDF表示,很难甚至不可能施加PDE边界条件(B(ucnn) = 0),因此物理约束学习将失败,特别是在标记数据稀缺甚至缺失的情况下。这是因为偏微分方程的解是由给定的BCs唯一确定的,如果没有适当的BCs,优化问题是无法实现的
- 当物理域(图1b中的蓝色区域)的形状远离其对应的矩形包络线时,从背景区域引入的伪影(图1b中的空白区域)可能会使训练过程复杂化,使优化更容易陷入不好的局部极小值。例如,在二进制表示中,在背景区域计算的导数总是零,因此求出的偏微分方程的解可能不正确
- 网格总是均匀的,不能根据物理来调整。例如在流体力学中,为了解决边界层问题,需要对边界附近的网格进行细化
- 虽然足够高的分辨率可以在一定程度上减少表示错误,缓解部分上述问题,但会显著增加训练成本,并导致记忆问题
- 传统统的栅格化/体素化方法对于输入的设计参数是不可微的,限制了其用于几何优化和设计目的。
 )
)
3.2 Physics-Informed Geometry-Adaptive Convolutional Neural Network
该方法核心思想是利用坐标变换技术将求解场从不规则物理域映射到矩形参考域。
3.2.1 Coordinate transformation between physical and reference domains
输入的正逆映射
x = G ( ξ ) , ξ = G − 1 ( x ) \mathbf{x}=\mathcal{G}(\boldsymbol{\xi}), \quad \boldsymbol{\xi}=\mathcal{G}^{-1}(\mathbf{x})x=G(ξ),ξ=G−1(x)
其中
G
:
Ω
r
↦
Ω
p
\mathcal{G}: \Omega_{r} \mapsto \Omega_{p}
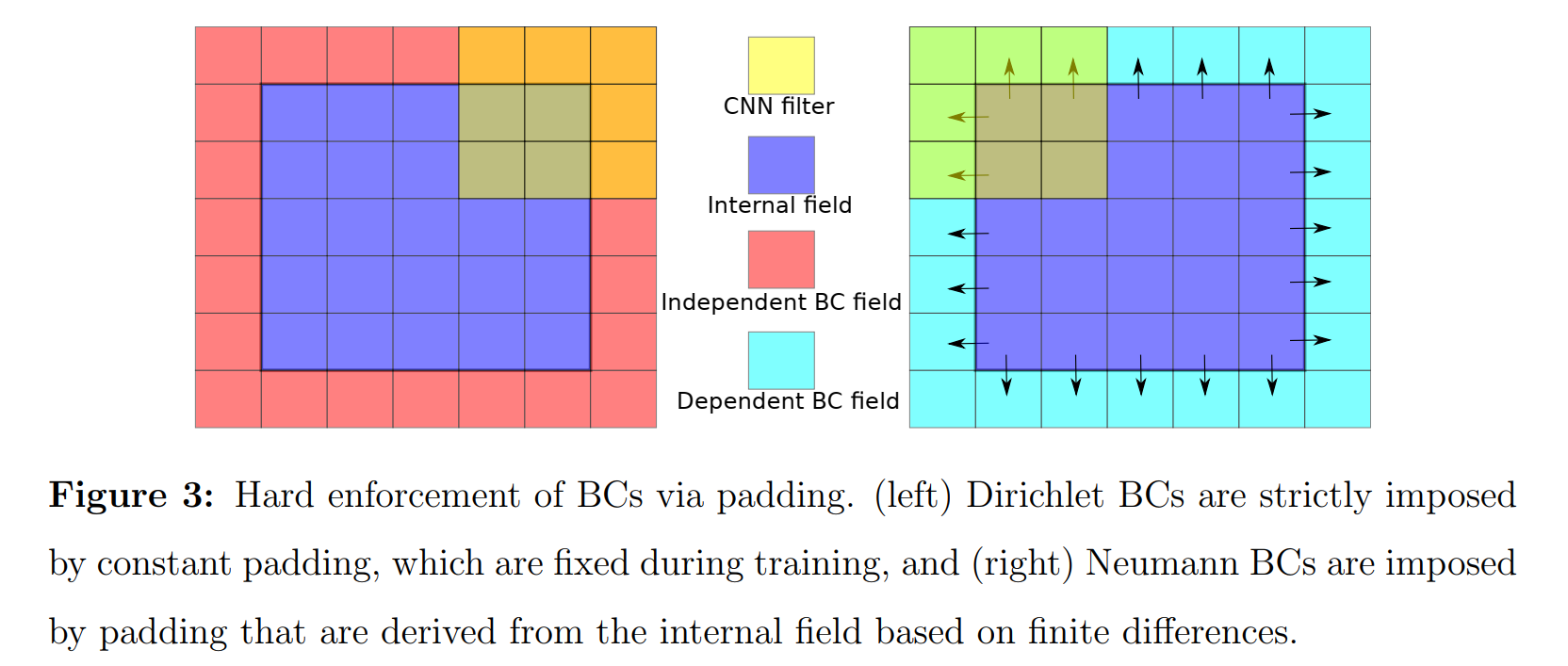
G:Ωr↦Ωpforward mapping,
Ω
p
↦
Ω
r
\Omega_{p} \mapsto \Omega_{r}
Ωp↦Ωr为inverse mapping,给定坐标变换函数(
9
/
9
−
1
9 / 9^{-1}
9/9−1),可以唯一地确 定从参考域到物理域的确定的一对一映射,并且变换映射的Jabobians也可用来重新表示参考域上的偏微分方 程。
The coordinates of the physical domain and reference domains are denoted by x ≐ [ x , y ] and ξ ≐ [ ξ , η ] \mathbf{x} \doteq[x, y] \text { and } \boldsymbol{\xi} \doteq[\xi, \eta] x≐[x,y] and ξ≐[ξ,η],对于边界
ξ ( x ) = ξ b for ∀ x ∈ ∂ Ω p i , i = 1 , ⋯ , 4 x ( ξ ) = x b for ∀ ξ ∈ ∂ Ω r i , i = 1 , ⋯ , 4 \begin{array}{l} \boldsymbol{\xi}(\mathbf{x})=\boldsymbol{\xi}_{b} \text { for } \forall \mathbf{x} \in \partial \Omega_{p}^{i}, i=1, \cdots, 4 \\ \mathbf{x}(\boldsymbol{\xi})=\mathbf{x}_{b} \text { for } \forall \boldsymbol{\xi} \in \partial \Omega_{r}^{i}, i=1, \cdots, 4 \end{array}ξ(x)=ξb for ∀x∈∂Ωpi,i=1,⋯,4x(ξ)=xb for ∀ξ∈∂Ωri,i=1,⋯,4(8,a,b)
如何来实现,举个例子, 9 − 1 9^{-1} 9−1可以由下列这个方程描述
∇ 2 ξ ( x ) = 0 \nabla^{2} \boldsymbol{\xi}(\mathbf{x})=0∇2ξ(x)=0 (9)
带有eq(8,a)的边界,通过交换Eq(9)中的自变量和因变量,可以得到以下物理坐标
x
x
x下的扩散方程:
α
∂
2
x
∂
ξ
2
−
2
β
∂
2
x
∂
ξ
∂
β
+
γ
∂
2
x
∂
η
2
=
0
α
∂
2
y
∂
ξ
2
−
2
β
∂
2
y
∂
ξ
∂
β
+
γ
∂
2
y
∂
η
2
=
0
\begin{aligned} \alpha \frac{\partial^{2} x}{\partial \xi^{2}}-2 \beta \frac{\partial^{2} x}{\partial \xi \partial \beta}+\gamma \frac{\partial^{2} x}{\partial \eta^{2}} &=0 \\ \alpha \frac{\partial^{2} y}{\partial \xi^{2}}-2 \beta \frac{\partial^{2} y}{\partial \xi \partial \beta}+\gamma \frac{\partial^{2} y}{\partial \eta^{2}} &=0 \end{aligned}
α∂ξ2∂2x−2β∂ξ∂β∂2x+γ∂η2∂2xα∂ξ2∂2y−2β∂ξ∂β∂2y+γ∂η2∂2y=0=0(10)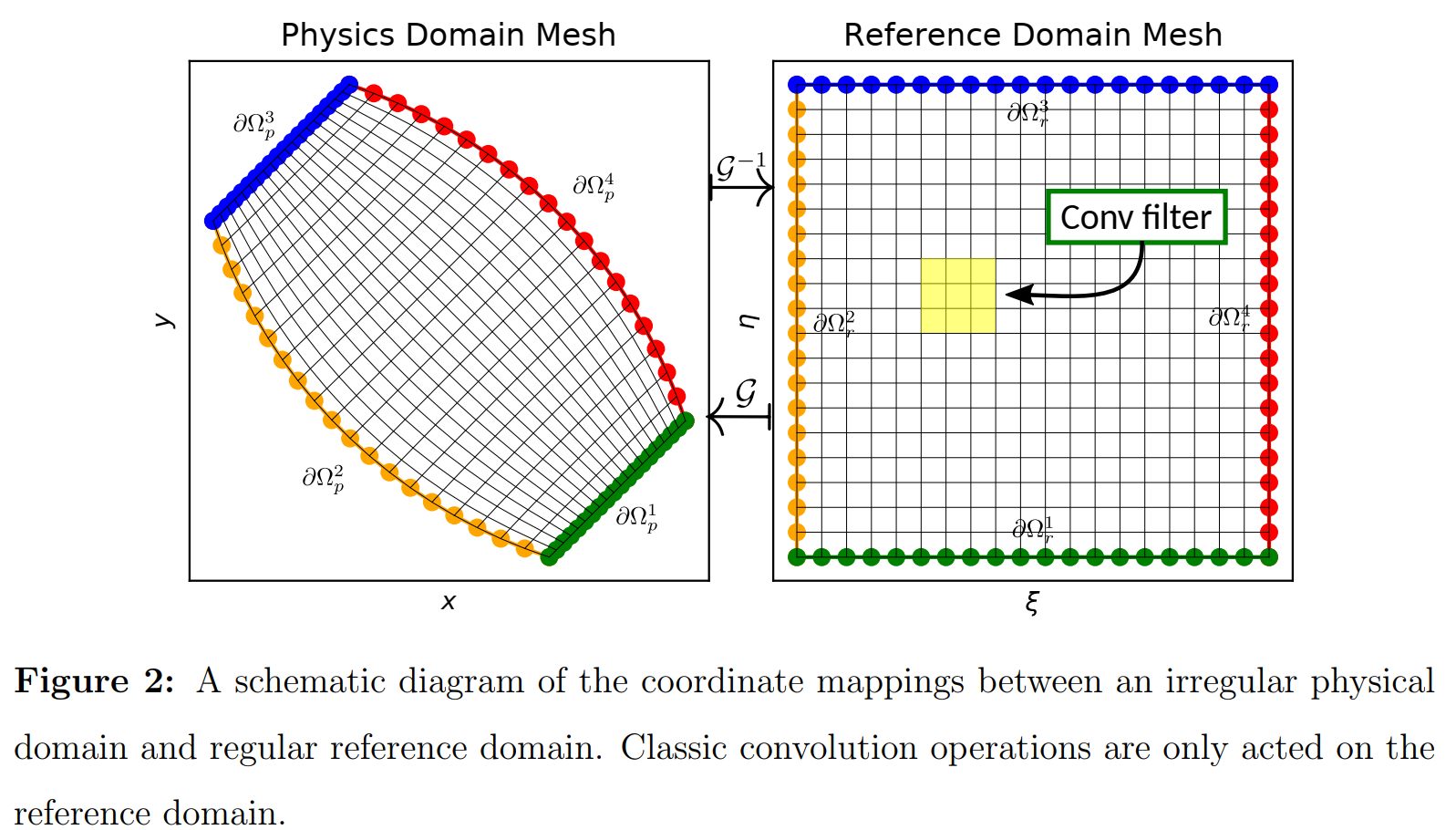
其中,
α
,
β
,
and
γ
\alpha, \beta, \text { and } \gamma
α,β, and γ
α
=
(
∂
x
∂
η
)
2
+
(
∂
y
∂
η
)
2
γ
=
(
∂
x
∂
ξ
)
2
+
(
∂
y
∂
ξ
)
2
β
=
∂
x
∂
ξ
∂
x
∂
η
+
∂
y
∂
ξ
∂
y
∂
η
\begin{aligned} \alpha &=\left(\frac{\partial x}{\partial \eta}\right)^{2}+\left(\frac{\partial y}{\partial \eta}\right)^{2} \\ \gamma &=\left(\frac{\partial x}{\partial \xi}\right)^{2}+\left(\frac{\partial y}{\partial \xi}\right)^{2} \\ \beta &=\frac{\partial x}{\partial \xi} \frac{\partial x}{\partial \eta}+\frac{\partial y}{\partial \xi} \frac{\partial y}{\partial \eta} \end{aligned}
αγβ=(∂η∂x)2+(∂η∂y)2=(∂ξ∂x)2+(∂ξ∂y)2=∂ξ∂x∂η∂x+∂ξ∂y∂η∂y
通过解带有边界(8)的eq(10),forward map的离散值就能获得.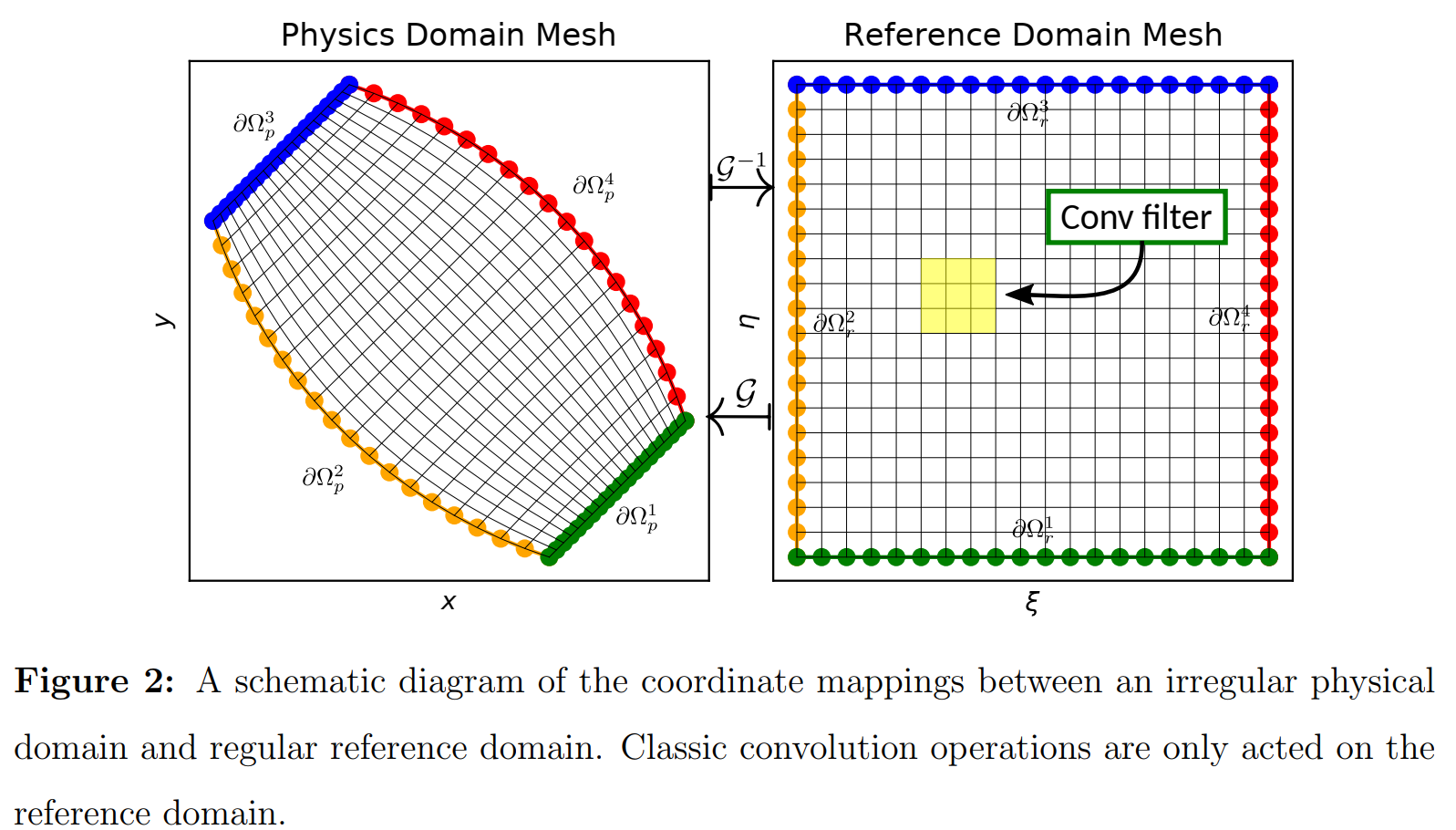
3.2.2 Reformulate physics-constrained learning on reference domain
在physics domain的微分方程要变成reference domain, **Jacobians of the transformation map **
9
9
9, 使得在physics domain的一阶导数转化为reference domain
∂
∂
x
=
(
∂
∂
ξ
)
(
∂
ξ
∂
x
)
+
(
∂
∂
η
)
(
∂
η
∂
x
)
∂
∂
y
=
(
∂
∂
ξ
)
(
∂
ξ
∂
y
)
+
(
∂
∂
η
)
(
∂
η
∂
y
)
\begin{aligned} \frac{\partial}{\partial x} &=\left(\frac{\partial}{\partial \xi}\right)\left(\frac{\partial \xi}{\partial x}\right)+\left(\frac{\partial}{\partial \eta}\right)\left(\frac{\partial \eta}{\partial x}\right) \\ \frac{\partial}{\partial y} &=\left(\frac{\partial}{\partial \xi}\right)\left(\frac{\partial \xi}{\partial y}\right)+\left(\frac{\partial}{\partial \eta}\right)\left(\frac{\partial \eta}{\partial y}\right) \end{aligned}
∂x∂∂y∂=(∂ξ∂)(∂x∂ξ)+(∂η∂)(∂x∂η)=(∂ξ∂)(∂y∂ξ)+(∂η∂)(∂y∂η) (12)
通常,有限差分用于数值计算雅可比矩阵,必须在参考域中执行,修改eq12为
∂
∂
x
=
1
J
⏟
constant
[
(
∂
∂
ξ
)
(
∂
y
∂
η
)
⏟
constant
−
(
∂
∂
η
)
(
∂
y
∂
ξ
)
⏟
constant
]
\frac{\partial}{\partial x}=\underbrace{\frac{1}{J}}_{\text {constant }}[\left(\frac{\partial}{\partial \xi}\right) \underbrace{\left(\frac{\partial y}{\partial \eta}\right)}_{\text {constant }}-\left(\frac{\partial}{\partial \eta}\right) \underbrace{\left(\frac{\partial y}{\partial \xi}\right)}_{\text {constant }}]
∂x∂=constant J1[(∂ξ∂)constant (∂η∂y)−(∂η∂)constant (∂ξ∂y)]
∂
∂
y
=
1
J
⏟
constant
[
(
∂
∂
η
)
(
∂
x
∂
ξ
)
⏟
constant
−
(
∂
∂
ξ
)
(
∂
x
∂
η
)
⏟
constant
]
\frac{\partial}{\partial y}=\underbrace{\frac{1}{J}}_{\text {constant }}[\left(\frac{\partial}{\partial \eta}\right) \underbrace{\left(\frac{\partial x}{\partial \xi}\right)}_{\text {constant }}-\left(\frac{\partial}{\partial \xi}\right) \underbrace{\left(\frac{\partial x}{\partial \eta}\right)}_{\text {constant }}]
∂y∂=constant J1[(∂η∂)constant (∂ξ∂x)−(∂ξ∂)constant (∂η∂x)]
其中
J
=
∂
x
∂
ξ
∂
y
∂
η
−
∂
x
∂
η
∂
y
∂
ξ
≠
0
J=\frac{\partial x}{\partial \xi} \frac{\partial y}{\partial \eta}-\frac{\partial x}{\partial \eta} \frac{\partial y}{\partial \xi} \neq 0
J=∂ξ∂x∂η∂y−∂η∂x∂ξ∂y=0是Jacobian matrix 的行列式,
∂
y
∂
η
,
∂
y
∂
ξ
\frac{\partial y}{\partial \eta}, \frac{\partial y}{\partial \xi}
∂η∂y,∂ξ∂y,
∂
x
∂
η
,
and
∂
x
∂
ξ
\frac{\partial x}{\partial \eta}, \text { and } \frac{\partial x}{\partial \xi}
∂η∂x, and ∂ξ∂x能预先计算,如果forward map确定就保持常数,
∂
∂
η
and
∂
∂
ξ
\frac{\partial}{\partial \eta} \text { and } \frac{\partial}{\partial \xi}
∂η∂ and ∂ξ∂在reference domain
在参考域的优化目标, 损失函数为
min
Γ
∑
i
=
1
n
d
∥
F
~
(
u
c
n
n
(
Ξ
,
μ
i
;
Γ
)
,
∇
u
c
n
n
(
Ξ
,
μ
i
;
Γ
)
,
∇
2
u
c
n
n
(
Ξ
,
μ
i
;
Γ
)
,
⋯
;
μ
i
)
∥
Ω
r
⏟
equation-based loss on reference domain:
L
~
p
d
e
s.t.
B
~
(
u
c
n
n
(
Ξ
,
μ
i
;
Γ
)
,
∇
u
c
n
n
(
Ξ
,
μ
i
;
Γ
)
,
∇
2
u
c
n
n
(
Ξ
,
μ
i
;
Γ
)
,
⋯
;
μ
i
)
=
0
,
on
∂
Ω
r
\begin{array}{l} \min _{\Gamma} \sum_{i=1}^{n_{d}} \underbrace{\left\|\tilde{\mathcal{F}}\left(\mathbf{u}^{c n n}\left(\boldsymbol{\Xi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla \mathbf{u}^{c n n}\left(\boldsymbol{\Xi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla^{2} \mathbf{u}^{c n n}\left(\boldsymbol{\Xi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \cdots ; \boldsymbol{\mu}_{i}\right)\right\|_{\Omega_{r}}}_{\text {equation-based loss on reference domain: } \tilde{\mathcal{L}}_{p d e}} \\ \text {s.t. } \tilde{\mathcal{B}}\left(\mathbf{u}^{c n n}\left(\boldsymbol{\Xi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla \mathbf{u}^{c n n}\left(\boldsymbol{\Xi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \nabla^{2} \mathbf{u}^{c n n}\left(\boldsymbol{\Xi}, \boldsymbol{\mu}_{i} ; \Gamma\right), \cdots ; \boldsymbol{\mu}_{i}\right)=0, \text { on } \partial \Omega_{r} \end{array}
minΓ∑i=1ndequation-based loss on reference domain: L~pde∥∥F~(ucnn(Ξ,μi;Γ),∇ucnn(Ξ,μi;Γ),∇2ucnn(Ξ,μi;Γ),⋯;μi)∥∥Ωrs.t. B~(ucnn(Ξ,μi;Γ),∇ucnn(Ξ,μi;Γ),∇2ucnn(Ξ,μi;Γ),⋯;μi)=0, on ∂Ωr
4 实验结果
∇
⋅
(
∇
T
(
x
)
)
=
0
,
x
∈
Ω
p
T
(
x
)
=
T
b
c
(
x
)
,
x
∈
∂
Ω
p
\begin{array}{l} \nabla \cdot(\nabla T(\mathbf{x}))=0, \mathbf{x} \in \Omega_{p} \\ T(\mathbf{x})=T_{b c}(\mathbf{x}), \mathbf{x} \in \partial \Omega_{p} \end{array}
∇⋅(∇T(x))=0,x∈ΩpT(x)=Tbc(x),x∈∂Ωp

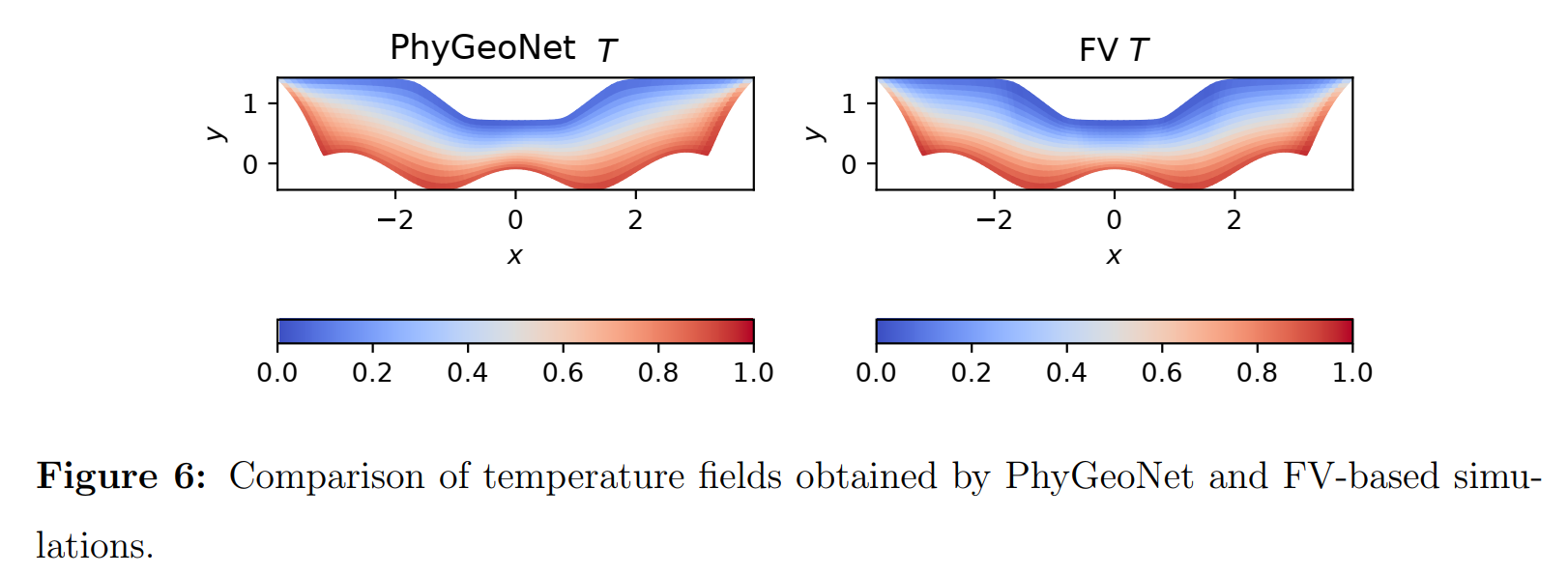
5 总结
- 主要就是解决了CNN求解域为非规则形状这样问题,同时将物理信息嵌入CNN中,实现了物理数据双驱动。
版权归原作者 pinn山里娃 所有, 如有侵权,请联系我们删除。