中科院一区顶刊！基于高斯量子改进的粒子群算法GQPSO！效果极佳！

** 声明：文章是从本人公众号中复制而来，因此，想最新最快了解各类智能优化算法及其改进的朋友，可关注我的公众号：强盛机器学习，不定期会有很多免费代码分享~**

目录

之前经常在论文里看到有将量子粒子群算法应用到各类领域的，但是用的人一旦多了，就没有什么创新性了，审稿人看了也会腻。另外，从测试函数的表现上来讲，量子粒子群相比于原始粒子群算法其实并没有特别明显的区别。

因此，今天给小伙伴带来一期发表在中科院SCI一区顶刊《Expert Systems with Applications 》上的算法：基于高斯量子行为改进的粒子群算法！它使用高斯变异算子代替随机序列，可以防止量子粒子群算法过早收敛到局部最优，是一种不错的改进方法！也能给审稿人眼前一亮的感觉！大家如果有需要也可以应用到各类预测、路径规划、分解等各类应用中！

本期代码包括了GQPSO与PSO两种算法以及23个标准测试函数，并在这些函数中进行测试，为公平起见，统一设置迭代次数为500，种群数量为30。同时为了防止作弊，全部列出前12个测试函数，无一遗漏！

废话不多说，先来看下效果！

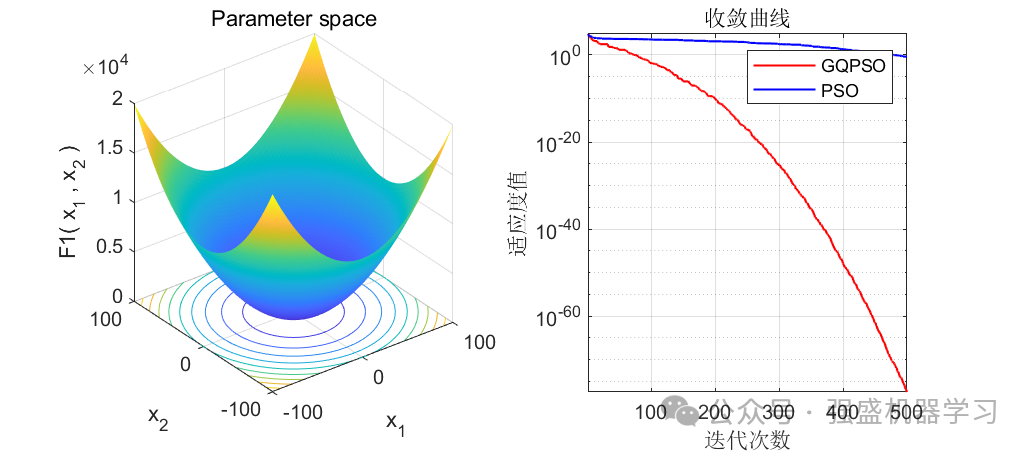
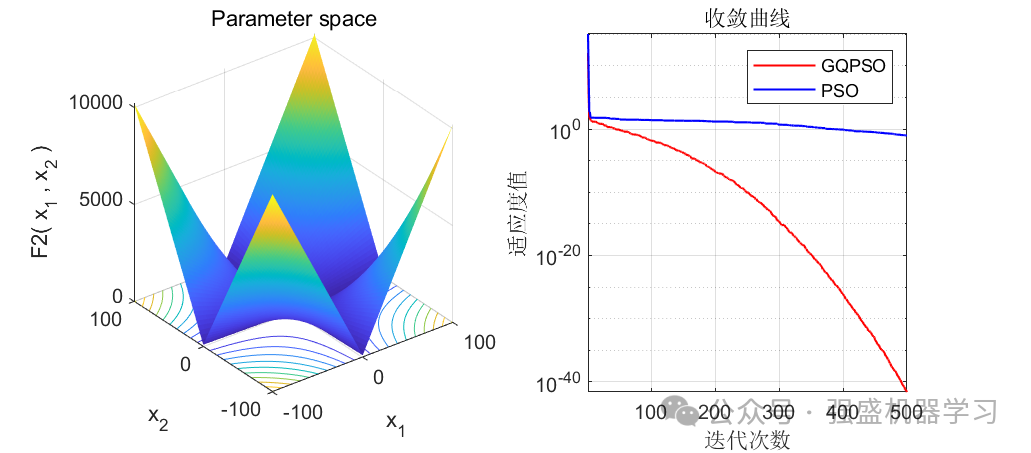
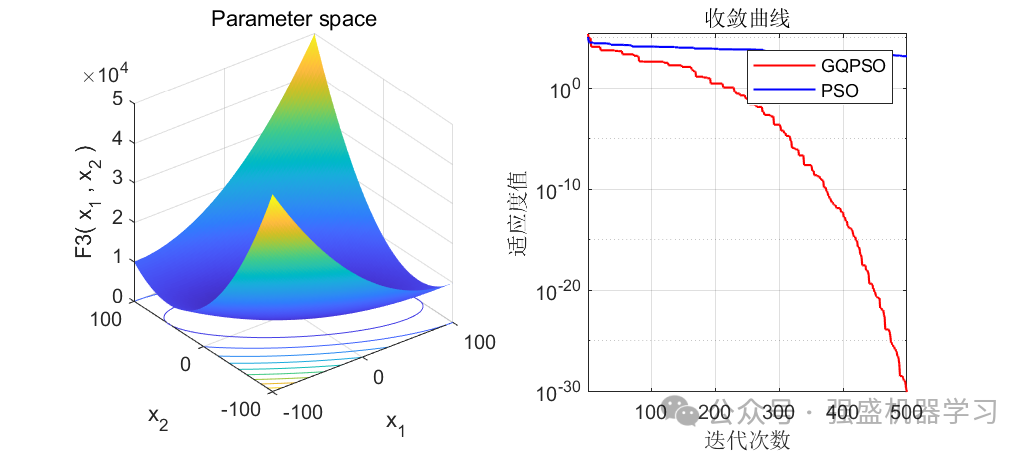
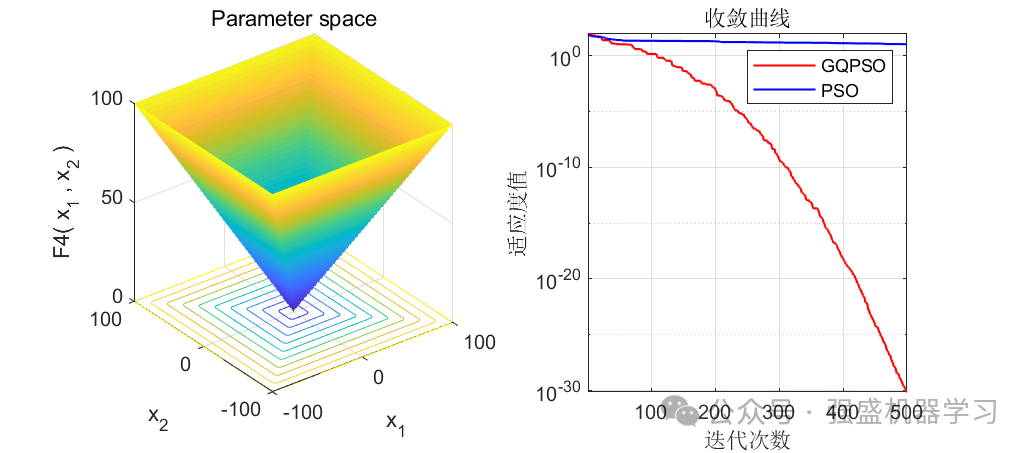
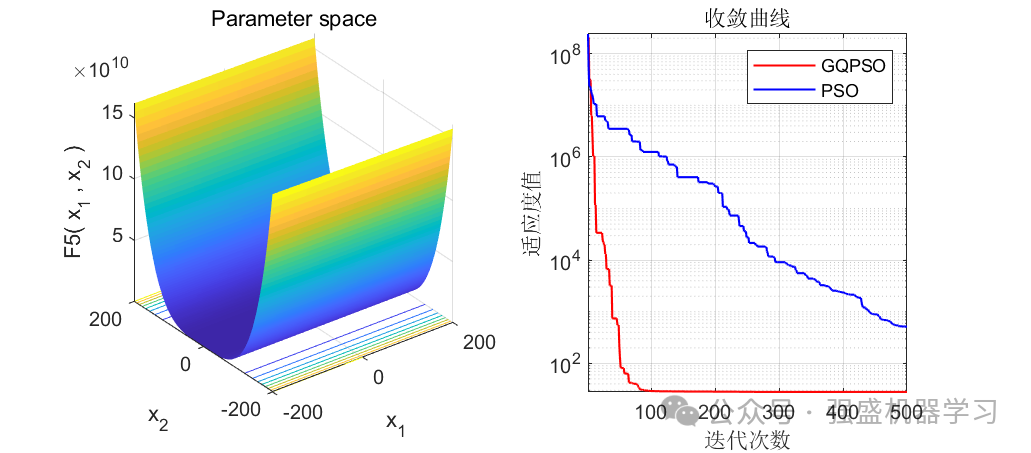
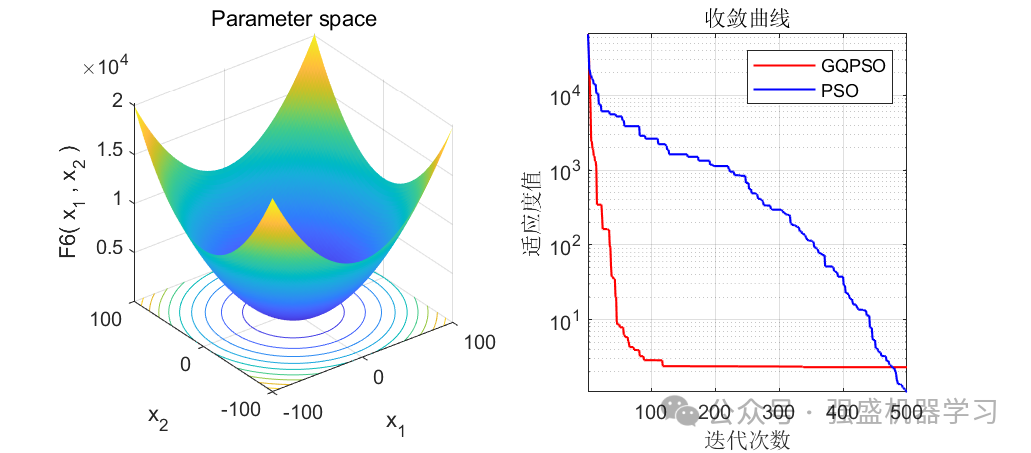
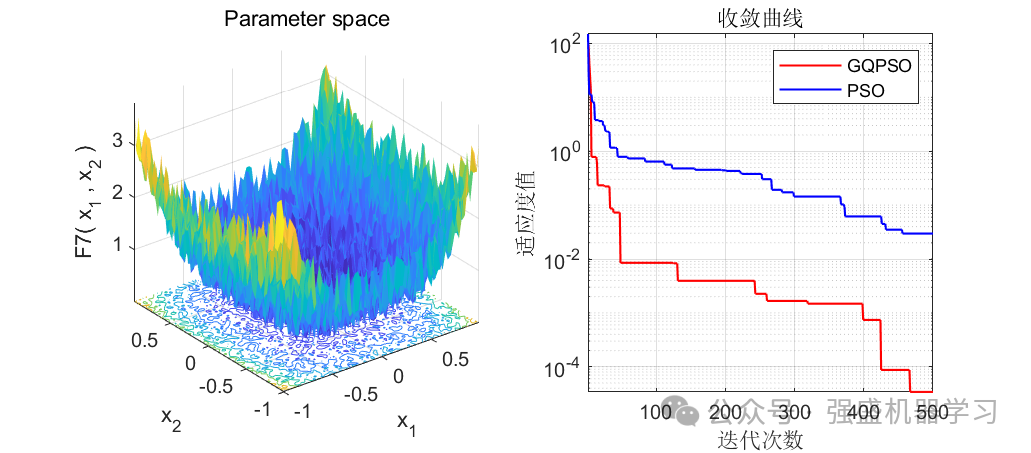
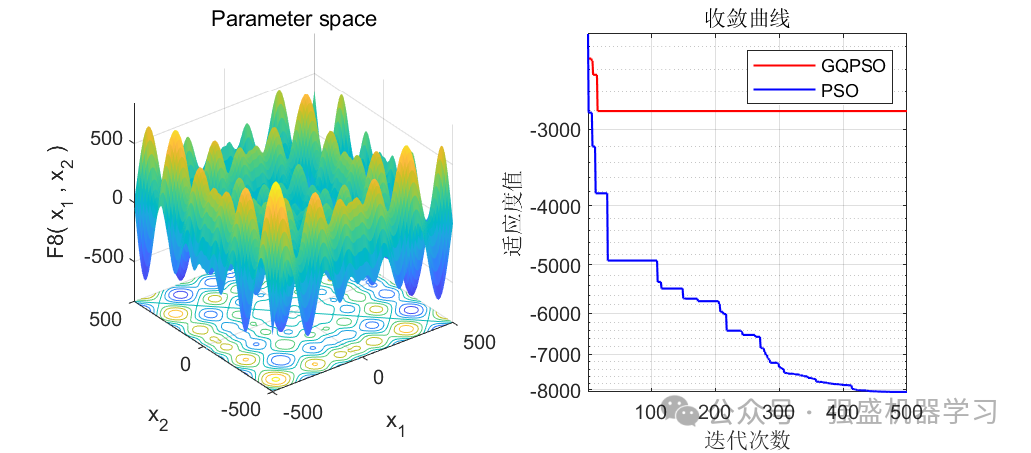
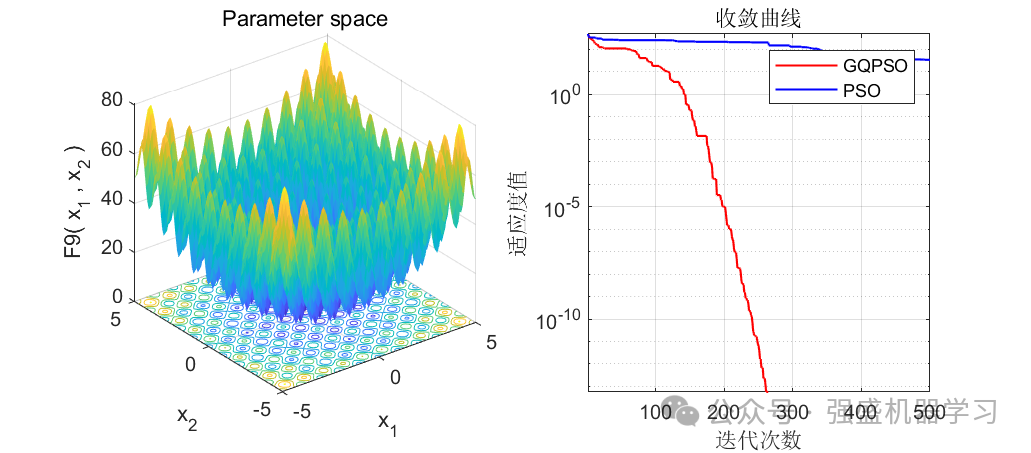
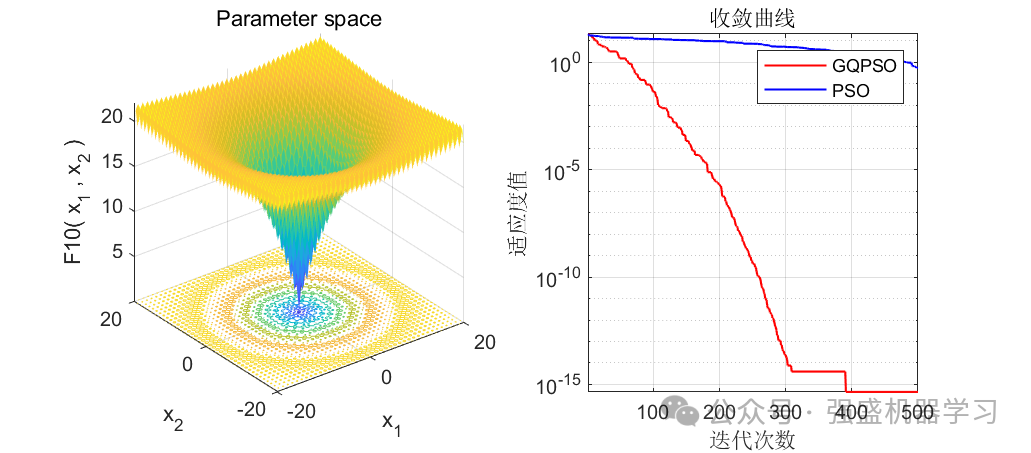
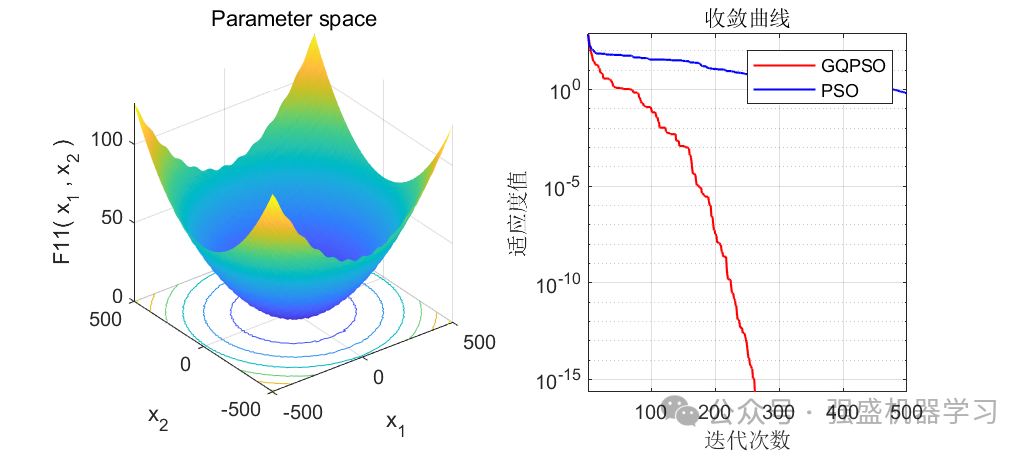
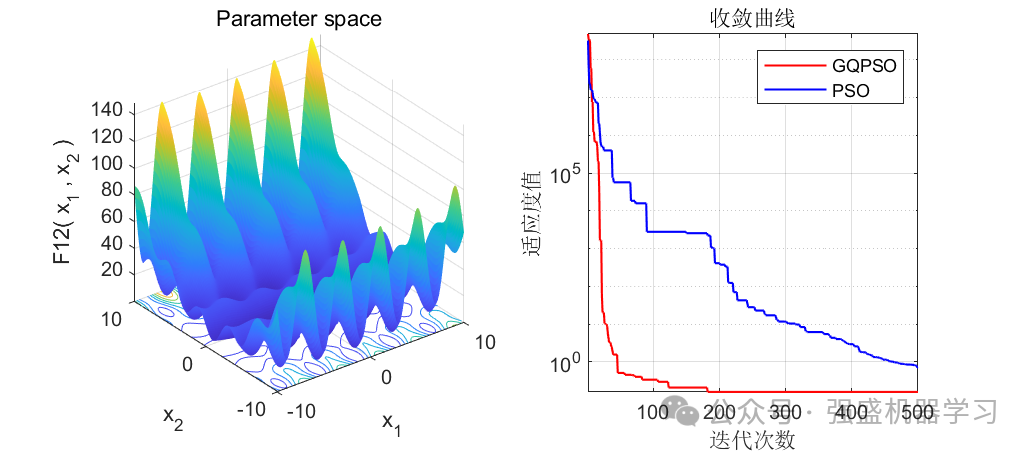
可以看到，前12个测试函数中，有10个都优于原来的PSO算法（当然你也不可能指望一个改进算法完全优于原始算法），在F9和F11中都直接找到了最优值0，且收敛速度相比于原算法也快很多！证明这个改进算法效果还是非常不错的！

其他的函数小伙伴们可以自行尝试，总体上效果明显优于原有的算术优化算法！

接下来详细讲解一下它的改进点！

量子粒子群算法

在PSO的量子模型中，粒子的状态由波函数(Schrödinger方程)描述，而不是位置和速度。换个通俗易懂的说法，就是原来粒子群是根据位置和速度的那一个主公式进行迭代的，而现在粒子按照以下主公式进行迭代迭代方：

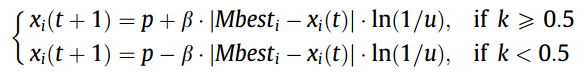
其中b为设计参数，称为收缩膨胀系数， u和k是在[0,1]范围内使用均匀概率分布函数生成的值。Mbest被定义为所有粒子最佳位置的平均值，它的计算方式为：

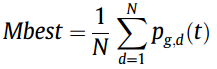
其中g表示群中所有粒子中最优粒子。在这种情况下，保证粒子群收敛的局部算子为如下公式：

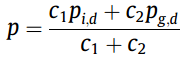
因此，QPSO（量子粒子群）的步骤为：

步骤1：初始化群体位置:使用均匀概率分布函数在n维问题空间中初始化具有随机位置的粒子群体(数组)。

步骤2：评价粒子的适应度:评价每个粒子的适应度值。一般来说，是最小化适应度函数。

步骤3：全局点更新:使用上式计算Mbest。

步骤4：与pbest比较：将每个粒子的适合度与粒子的pbest进行比较。如果当前值优于pbest，则将pbest值设置为当前值，并将pbest位置设置为n维空间中的当前位置。

步骤5：与gbest的比较：将适应度与总体上以前的最佳值进行比较。如果当前值优于gbest，则将gbest重置为当前粒子的数组索引和值。

步骤6：更新粒子位置：改变粒子的位置，其中c1和c2是在[0,1]范围内均匀概率分布生成的两个随机数。

步骤7：重复迭代循环：循环到步骤2，直到满足停止条件，通常是足够好的适应度或最大迭代次数。

高斯变异算子改进的量子粒子群算法

刚刚说完了原始的量子粒子群算法QPSO的原理，接下来看下我们的高斯量子粒子群算法是如何改进的：

以往，大多数粒子群算法使用均匀概率分布来生成随机数，而这里利用高斯概率分布给出了QPSO中突变算子的新结果。

对于PSO的随机系数，使用均值为零、单位方差的高斯分布序列生成随机数，可以在当前点周围生成具有大概率小振幅和具有小概率高振幅的步长，提供一个很好的折衷解，可以使粒子远离当前点并逃离局部极小值。

首先利用零均值、单位方差的高斯概率分布的绝对值生成随机数。这些结合高斯突变算子的QPSO新方法描述如下:

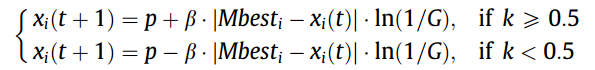
其中G=abs(N(0,1))。

刚刚的参数p改为：

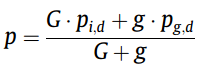
其中g=abs(N(0,1))。其余参数不变。

参考文献

[1]dos Santos Coelho L. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems[J]. Expert Systems with Applications, 2010, 37(2): 1676-1683.

部分代码展示

%% 清除环境变量
clear
clc
close all
addpath(genpath(pwd));
​
%% 参数设置
number = 'F1';                                                %  选定优化函数，自行替换:F1~F23
[lb,ub,variables_no,fobj] = Get_Functions_details(number);    %  [lb,ub,D,y]：下界、上界、维度、目标函数表达式
pop_size = 30;                                                %  种群数量 
max_iter = 500;                                               %  迭代次数
​
%% 运行各算法
[GQPSO_Best_score,GQPSO_Best_pos,GQPSO_curve] = GQPSO(pop_size,max_iter,lb,ub,variables_no,fobj);  % 改进粒子群优化算法
[PSO_Best_score,GQPSO_Best_pos,PSO_curve] = PSO(pop_size,max_iter,lb,ub,variables_no,fobj);        % 原始粒子群优化算法
​
%% 显示结果
display(['GQPSO在函数' [num2str(number)],'上的最优值', num2str(GQPSO_Best_score)]);
display(['PSO在函数' [num2str(number)],'上的最优值', num2str(PSO_Best_score)]);
​
%% 画图
figure('Position',[500 500 660 290])
% 三维函数图
subplot(1,2,1);
func_plot(number);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([number,'( x_1 , x_2 )'])

完整代码获取

**如果需要获得图中的完整代码，只需点击下方小卡片，再回复关键字，不区分大小写： **

GQPSO

也可回复个人需求（比如GQPSO-LSTM）定制以下高斯量子粒子群算法优化模型（看到秒回）：

1.回归/时序/分类预测类：SVM、RVM、LSSVM、ELM、KELM、HKELM、DELM、RELM、DHKELM、RF、SAE、LSTM、BiLSTM、GRU、BiGRU、PNN、CNN、BP、XGBoost、TCN、BiTCN、ESN等等均可~

2.组合预测类：CNN/TCN/BiTCN/DBN/Adaboost结合SVM、RVM、ELM、LSTM、BiLSTM、GRU、BiGRU、Attention机制类等均可（可任意搭配非常新颖）~

3.分解类：EMD、EEMD、VMD、REMD、FEEMD、TVFEMD、CEEMDAN、ICEEMDAN、SVMD、FMD等分解模型均可~

4.路径规划类：机器人路径规划、无人机三维路径规划、冷链物流路径优化、VRPTW路径优化等等~

​5.优化类：光伏电池参数辨识优化、储能容量配置优化、微电网优化、PID参数整定优化、无线传感器覆盖优化、故障诊断等等均可~~

6.原创改进优化算法（适合需要创新的同学）：原创改进粒子群优化算法PSO以及蛇鹫SBOA、蜣螂DBO等任意优化算法均可，保证测试函数效果！