Diffusion Models：生成扩散模型

Diffusion Models：生成扩散模型

当前的内容是梳理《Transformer视觉系列遨游》系列过程中引申出来的。目前最近在AI作画这个领域 Transformer 火的一塌糊涂，AI画画效果从18年的 DeepDream[1] 噩梦中惊醒过来，开始从2022年 OpenAI 的 DALL·E 2[2] 引来插画效果和联想效果都达到惊人效果。虽然不懂，但是这个话题很吸引ZOMI，于是就着这个领域内容来看看有什么好玩的技术点。

但是要了解：Transformer 带来AI+艺术，从语言开始遇到多模态，碰撞艺术火花 这个主题，需要引申很多额外的知识点，可能跟 CV、NLP 等领域大力出奇迹的方式不同，AI+艺术会除了遇到 Transformer 结构以外，还会涉及到 VAE、ELBO、Diffusion Model等一系列跟数学相关的知识。

Transformer + Art系列中，今天新挖一个 Diffusion Models 的坑，跟 VAE 一样原理很复杂，实现很粗暴。据说生成扩散模型以数学复杂闻名，似乎比 VAE、GAN 要难理解得多，是否真的如此？扩散模型能少来点数学吗？扩散模型真的做不到一个简单点的理解吗？

在本文中，我们将研究扩散模型的理论基础，然后演示如何在 PyTorch 中使用扩散模型生成图像。Let's dive in!

Diffusion Model 基本介绍

扩散模型（Diffusion Models）发表以来其实并没有收到太多的关注，因为他不像 GAN 那样简单粗暴好理解。不过最近这几年正在生成模型领域异军突起，当前最先进的两个文本生成图像——OpenAI 的 DALL·E 2和 Google 的 Imagen，都是基于扩散模型来完成的。

如今生成扩散模型的大火，则是始于2020年所提出的 DDPM（Denoising Diffusion Probabilistic Model），仅在 2020 年发布的开创性论文 DDPM 就向世界展示了扩散模型的能力，在图像合成方面击败了 GAN[6]，所以后续很多图像生成领域开始转向 DDPM 领域的研究。

看了下网上很多文章在介绍 DDPM 时，上来就引入概率转移分布，接着就是变分推断，然后极大值似然求解和引入证据下界（Evidence Lower Bound）。一堆数学记号下来，先吓跑了前几周的我（当然，从这种介绍我们可以再次看出，DDPM 实际上与 VAE 的理论关系是非常紧密），再加之人们对传统扩散模型的固有印象，所以就形成了“需要很高深的数学知识”的错觉。

生成模型对比

还是先横向对一下最近比较火的几个生成模型 GAN、VAE、Flow-based Models、Diffusion Models。

GAN 由一个生成器（generator）和判别器（discriminator）组成，generator 负责生成逼真数据以“骗”过 discriminator，而 discriminator 负责判断一个样本是真实的还是“造”出来的。GAN 的训练其实就是两个模型在相互学习，能不能不叫“对抗”，和谐一点。

VAE 同样希望训练一个生成模型 x=g(z)，这个模型能够将采样后的概率分布映射到训练集的概率分布。生成隐变量 z，并且 z 是及含有数据信息又含有噪声，除了还原输入的样本数据以外，还可以用于生成新的数据。

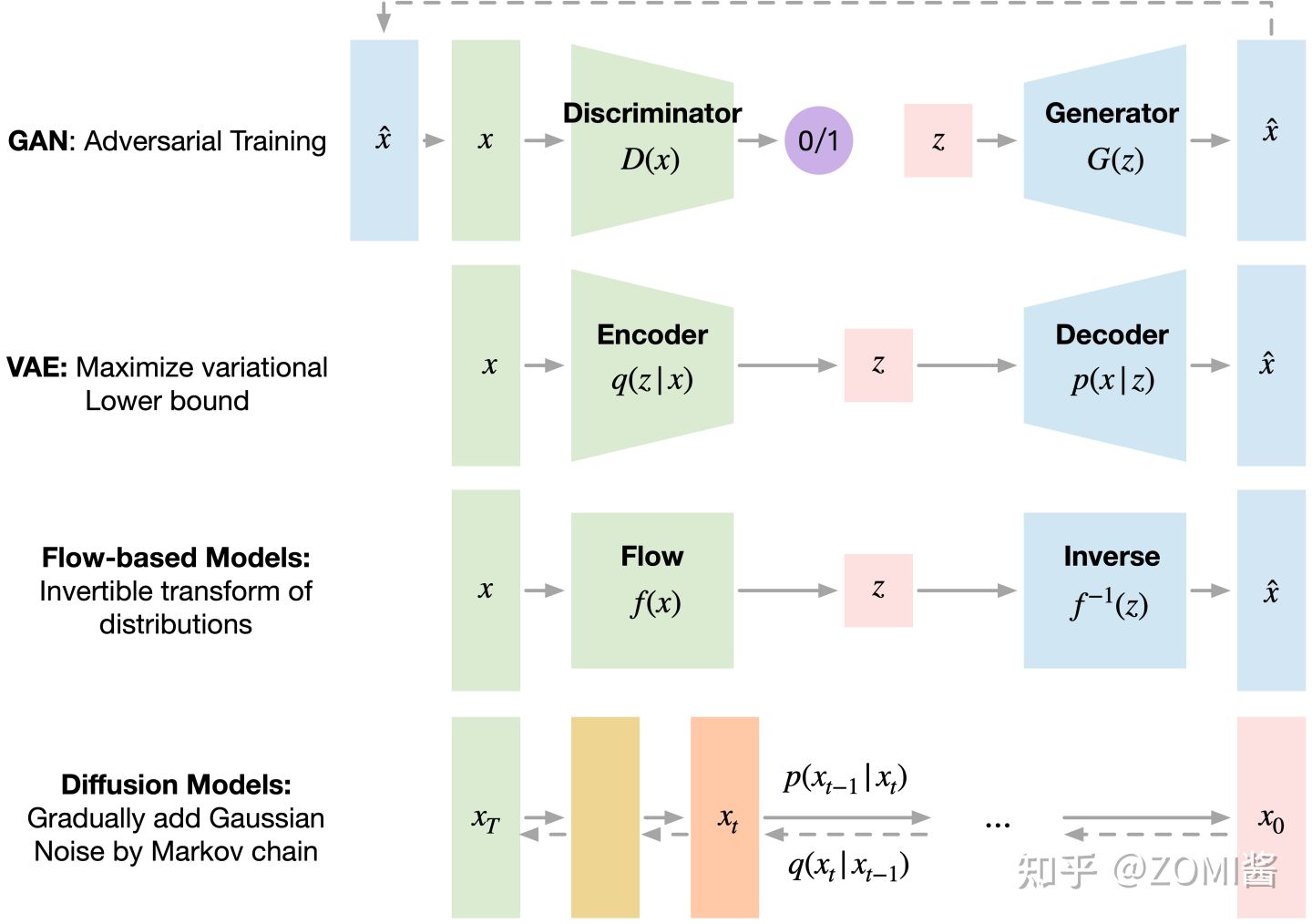
Diffusion Models 的灵感来自 non-equilibrium thermodynamics （非平衡热力学）。理论首先定义扩散步骤的马尔可夫链，以缓慢地将随机噪声添加到数据中，然后学习逆向扩散过程以从噪声中构造所需的数据样本。与 VAE 或流模型不同，扩散模型是通过固定过程学习，并且隐空间 z 具有比较高的维度。

总的来看，Diffusion Models 领域正处于一个百花齐放的状态，这个领域有一点像 GAN 刚提出来的时候，目前的训练技术让 Diffusion Models 直接跨越了 GAN 领域调模型的阶段，直接可以用来做下游任务。

基本介绍

Diffusion Models 既然叫生成模型，这意味着 Diffusion Models 用于生成与训练数据相似的数据。从根本上说，Diffusion Models 的工作原理，是通过连续添加高斯噪声来破坏训练数据，然后通过反转这个噪声过程，来学习恢复数据。

训练后，可以使用 Diffusion Models 将随机采样的噪声传入模型中，通过学习去噪过程来生成数据。也就是下面图中所对应的基本原理，不过这里面的图仍然有点粗。

更具体地说，扩散模型是一种隐变量模型（latent variable model），使用马尔可夫链（Markov Chain, MC）映射到 latent space。通过马尔科夫链，在每一个时间步 t 中逐渐将噪声添加到数据 xi 中以获得后验概率 q(x1:T∣x0) ，其中 x1,…,xT 代表输入的数据同时也是 latent space。也就是说 Diffusion Models 的 latent space 与输入数据具有相同维度。

马尔可夫链（Markov Chain, MC）是概率论和数理统计中具有马尔可夫性质（Markov property）且存在于离散的指数集（index set）和状态空间（state space）内的随机过程（stochastic process）。

Diffusion Models 分为正向的扩散过程和反向的逆扩散过程。下图为扩散过程，从 x0 到最后的 xT 就是一个马尔科夫链，表示状态空间中经过从一个状态到另一个状态的转换的随机过程。而下标则是 Diffusion Models 对应的图像扩散过程。

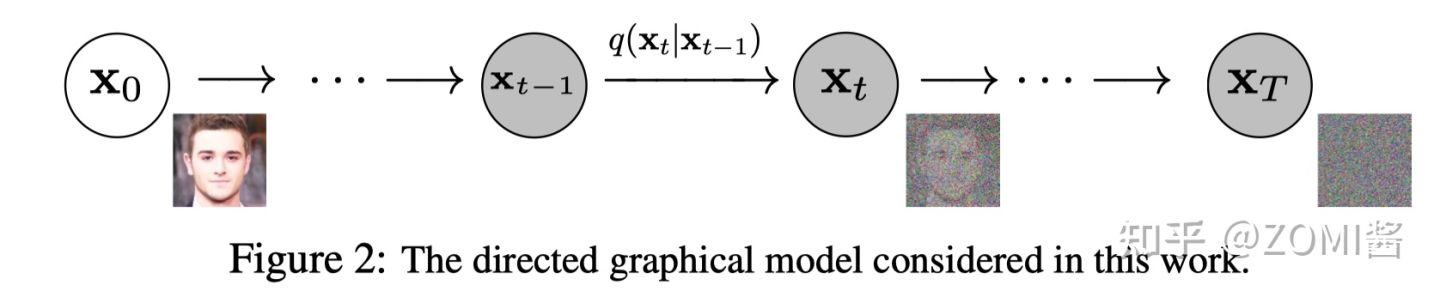
最终，从 x0 输入的真实图像，经过 Diffusion Models 后被渐近变换为纯高斯噪声的图片 xT 。

模型训练主要集中在逆扩散过程。训练扩散模型的目标是，学习正向的反过程：即训练概率分布 pθ(xt−1∣xt) 。通过沿着马尔科夫链向后遍历，可以重新生成新的数据 x0 。读到这里就有点意思啦，Diffusion Models 跟 GAN 或者 VAE 的最大区别在于不是通过一个模型来进行生成的，而是基于马尔科夫链，通过学习噪声来生成数据。

除了生成很好玩的高质量图片之外呢，Diffusion Models 还具有许多其他好处，其中最重要的是训练过程中不需要再对抗了，整个世界都感觉和平了。因为对于 GAN 网络模型来说，对抗性训练其实是很不好调试的，因为对抗训练过程互相博弈的两个模型，对我们来说是个黑盒子。另外在训练效率方面，扩散模型还具有可扩展性和可并行性，那这里面如何加速训练过程，如何添加更多数学规则和约束，扩展到语音、文本、三维领域就很好玩了，可以出很多新文章。

详解 Diffusion Model

上面已经清晰表示了 Diffusion Models 由正向过程（或扩散过程）和反向过程（或逆扩散过程）组成，其中输入数据逐渐被噪声化，然后噪声被转换回源目标分布的样本。

如果不想深入了解数学原理的可以直接跳过到代码实现部分。如果还是想了解一些基础的数学原理，那么可以接着继续看，其实没比 GAN 难多少，就是个马尔科夫链 + 条件概率分布。核心在于如何使用神经网络模型，来求解马尔科夫过程的概率分布。

扩散和逆扩散过程

前向过程由于每个时刻 t 只与 t-1 时刻有关，所以可以看做马尔科夫过程，在马尔科夫链的前向采样过程中，也就是扩散过程中可以将数据转换为高斯分布。即扩散过程通过 T 次累积对输入数据 xi 添加高斯噪声，将这个跟马尔可夫假设相结合，于是可以对扩散过程表达成：

(1)q(x1:T∣x0):=∏t=1Tq(xt∣xt−1):=∏t=1TN(xt;1−βtxt−1,βtI)

其中 β1,…,βT 是高斯分布方差的超参数。在扩散过程中，随着 t 的增大， xt 越来越接近纯噪声。当 T 足够大的时候， xT 可以收敛为标准高斯噪声 N(0,I) 。

不过呢，扩散模型的神奇“魔力”来自逆扩散过程。如果说扩散过程是加噪的过程，那么逆扩散过程就是去噪推断过程。如果我们能够逐步得到逆转后的分布 pθ(xt−1∣xt) ，就可以从标准高斯分布 N(0,I) 还原出样本数据的分布 x0 。

也就是在训练时候，模型学习逆扩散过程的概率分布，以生成新数据。如下图所示，从纯高斯噪声 p(xT):=N(xT;0,I) 开始，模型将学习联合概率分布 pθ(xT:0) ：

(2)pθ(xT:0):=p(xT)∏t=1Tpθ(xt−1∣xt):=p(xT)∏t=1TN(xt−1;μθ(xt,t),Σθ(xt,t))

根据马尔可夫规则表示，逆扩散过程当前时间步 t 只取决于上一个时间步 t-1，所以有：

(3)pθ(xt−1∣xt):=N(xt−1;μθ(xt,t),Σθ(xt,t))

现在我们其实已经简单搞清楚了 Diffusion Models 的扩散过程和逆扩散过程，也就是扩散过程中，人工添加一点点噪声直到数据为纯高斯噪声；逆扩散过程学习逆转后的分布，逐步地恢复样本数据。

不过，马尔科夫过程最麻烦的就是求解了，一般会用蒙特卡洛法进行采样，然后再去评估采样的结果好坏。上面的 Diffusion Models 会不会太理想啦？

训练方式

搞清楚逆扩散过程之后，现在算是搞清楚去噪推断过程。但是如何训练 Diffusion Models 以求得公式 (3) 中的均值 μθ(xt,t) 和方差 Σθ(xt,t) 呢？

在 VAE 中我们学过极大似然估计的作用：对于真实的训练样本数据已知，要求模型的参数，可以使用极大似然估计。Diffusion Models 通过极大似然估计，来找到逆扩散过程中马尔科夫链转换的概率分布，这就是 Diffusion Models 的训练目的。即最大化模型预测分布的对数似然：

(4)L=Eq[−log⁡pθ(x0)]

对于神经网络模型来说，一般优化的方式是通过损失函数求解网络模型的最小值，求最大化期望不太好使。于是换个思路，求模型的极大似然估计，等同于求解最小化负对数似然的变分上限 Lvlb （Variational Upper Bound）：

(5)E[−log⁡pθ(x0)]≤Eq[−log⁡pθ(x0:T)q(x1:T∣x0)]=:Lvlb

因为变分上界比较难求，但是 VAE 的推导中介绍过其实可以通过 KL散度来表示上界。那到这里为止，**最小化 **Lvlb 即可最小化 Diffusion Models 的目标损失。

看到公式 (5) 会不会觉很熟悉，下面讲讲两个小概念，再引入如何求解最小化变分上限 Lvlb。

什么是KL散度呢？

我们回顾一下， KL 散度是一种不对称统计距离度量，用于衡量一个概率分布 P 与另外一个概率分布 Q 的差异程度。之所以想根据 KL 散度来求解 Lvlb，是因为根据 Diffusion Models 的定义马尔可夫链中的转移分布属于高斯分布，而 KL 散度则可以用来计算2个高斯分布之间的差异距离。

连续分布的 KL 散度的数学形式是：

(6)DKL(P‖Q)=∫−∞∞p(x)log⁡(p(x)q(x))dx

用 KL 散度来表示变分上界

根据 Diffusion Models 最早提出的一篇文章[1]，进一步对 Lvlb 推导，可以得到变分上限为熵与多个KL散度的累加，根据 KL 散度重写变分上限有：

(7)Lvlb=L0+L1+…+LT−1+LT

其中有：

(8)L0=−log⁡pθ(x0∣x1)

(9)Lt−1=DKL(q(xt−1∣xt,x0)‖pθ(xt−1∣xt))

(10)LT=DKL(q(xT∣x0)‖p(xT))

x0 都会出现在扩散过程中的 Lt−1 ，现在所有 KL 散度都是在高斯概率分布之间进行比较。 这意味着可以使用闭包表达式，而不是采样的蒙特卡洛估计方式来精确计算变分上界。

到这里看不懂没关系，想表达的是最小化 Lvlb 即可最小化 Diffusion Models 的目标损失，而求解 Lvlb 则可以通过计算 KL 散度来代替。

有了目标函数的数学基础后，现在需要就如何实现扩散模型训练过程有几个细节：

1. 对于正向扩散过程，唯一需要的选择是概率相关的向量（均值和方差），其值在扩散过程中在隐变量 xt 中直接添加高斯参数 βt 。
2. 对于逆扩散过程，需要选择能够表达高斯分布的模型结构，神经网络模型的拟合能力很强，于是就可以引入神经网络模型啦。
3. 最后就是对于神经网络模型有一个简单的要求，模型的输入、输出、中间隐变量必须要有相同的维度 dims。

损失函数和 LT

既然有神经网络模型，那自然离不开损失函数，有了损失函数就有了优化的方向和目标，下面来展开损失函数的定义。

在扩散过程公式（1）中，其中 β1,…,βT 是高斯分布方差的超参数。且实际中 βt 随着 t 增大是递增的，即 β1<…<βT 。在实际代码中，我们设置 βt 是从 0.0001 到0.02 线性插值。

在逆扩散过程公式（10）中，时间步 T 中前，由于前向扩散过程中 q 没有可学习参数，只是单纯添加高斯噪声，而最后时间步 T 得到的 xT 则是纯高斯噪声，因此在训练的过程中 LT 可以当做常量忽略。即下面公式不需要：

LT=DKL(q(xT∣x0)‖p(xT)):=0

回顾公式（3），把反向马尔科夫过程转变为高斯分布来表示：

(3)pθ(xt−1∣xt):=N(xt−1;μθ(xt,t),Σθ(xt,t))

在求解（训练）的过程需要知道得到高斯分布的均值 μθ(xt,t) 和方差 Σθ(xt,t) 。对于方差 Σ 不好求解，DDPM 论文中直接使用 βt 来代替：

(11)Σθ(xt,t)=σt2Iσt2=βt

假设多元高斯是具有相同方差的独立高斯的乘积，方差值可以随时间变化。基于这个假设可以将逆扩散过程的方差，设置为与正向扩散过程方差相同，得到公式（11）。不过有意思的是在实际代码中因为引入了神经网络，所以可以通过训练的方式来得到方差 Σ 。

数学上，假设使用 βt 来代替方差 Σθ ，因此有：

(12)pθ(xt−1∣xt):=N(xt−1;μθ(xt,t),Σθ(xt,t):=N(xt−1;μθ(xt,t),σt2I)

那现在就更清楚啦，可以将KL散度：

(13)Lt−1=DKL(q(xt−1∣xt,x0)‖pθ(xt−1∣xt))

转换为：

(14)Lt−1∝‖μ~t(xt,x0)−μθ(xt,t)‖2

由正向扩散过程我们知道，任意时刻的 xt 可以由 x0 和 β 表示。参数 μθ 最直接的表示是预测扩散模型的后验概率的均值。不过在实际测试当中，DDPM 作者发现通过训练以在任何给定时间步 t 预测噪声分量 μθ 会产生更好的结果。设：

(15)μθ(xt,t)=1αt(xt−βt1−α¯tϵθ(xt,t))

其中：

(16)αt:=1−βt and α¯t:=∏s=1tαs

因此可以得到损失函数 L，使得训练更加稳定：

(17)Lsimple (θ):=Et,x0,ϵ[‖ϵ−ϵθ(α¯tx0+1−α¯tϵ,t)‖2]

高斯分布 ϵ 为神经网络模型所预测的噪声（用于去噪），可看做为 ϵθ(xt,t)。***Diffusion Models 训练的核心就是取学习高斯噪声 *ϵ,ϵθ 之间均方误差 MSE**。

实际训练过程和 L0

上面已经说过啦，在逆扩散过程中，马尔科夫过程表示为由连续条件高斯分布下的累积变换组成。有了总体的优化策略，还要看每个像素的计算方式，在逆扩散过程结束时，我们希望得到一张生成好的图像，因此需要设计一种方法，使得图像上每个像素值都满足离散的对数似然。

为了达到这个目的，将逆扩散过程中的最后从 x1 到 x0 的转换设置为独立的离散计算方式。 即在最后一个转换过程在给定 x_1$ x1 下得到图像 x0 满足对数似然，假设像素与像素之间是相互独立的：

(18)pθ(x0∣x1)=∏i=1Dpθ(x0i∣x1i)

式 (18) 中 D 是输入数据的维数，上标 i 表示图像中的一个坐标位置。现在的目标是确定给定像素的值可能性有多大，也就是想要知道对应时间步 t=1 下噪声图像 x 中相应像素值的分布：

(19)N(x;μθi(x1,1),σ12)

其中 t = 1 的像素分布来自多元高斯分布，其对角协方差矩阵允许我们将分布拆分为单变量高斯的乘积：

(20)N(x;μθ(x1,1),σ12I)=∏i=1DN(x;μθi(x1,1),σ12)

现在假设图像已经从0-255的数值之间，经过归一化在[-1,1]的范围内。在 t=0 时给定每个像素的像素值，最后一个时间步 t=1 的转换概率分布 pθ(x0∣x1) 的值就是每个像素值的乘积。简而言之，这个过程由等式简洁 (18) 地表示：

(21)pθ(x0∣x1)=∏i=1Dpθ(x0i∣x1i)=∏i=1D∫δ−(x0i)δ+(xii)N(x;μθi(x1,1),σ12)dx

其中约束有：

δ−(x)={−∞x=−1x−1255x>−1

和：

δ+(x)={∞x=1x+1255x<1

那现在我们就可以计算公式 (8) 中，最后的转换概率分布 pθ(x0∣x1) 的值。

训练过程如图左边 Algorithm 1 Training部分：

1. 从标准高斯分布采样一个噪声 ϵ∼N(0,I) ；
2. 通过梯度下降最小化损失 ∇θ|ϵ−zθ(α¯tx0+1−α¯tϵ,t)|2 ；
3. 训练到收敛为止（训练时间比较长，T代码中设置为1000）

测试（采样）如图右边 Algorithm 2 Sampling部分：

1. 从标准高斯分布采样一个噪声 xT∼N(0,I) ；
2. 从时间步 T 开始正向扩散迭代到时间步 1；
3. 如果时间步不为1，则从标准高斯分布采样一个噪声 z∼N(0,I) ，否则 z=0；
4. 根据高斯分布计算每个时间步 t 的噪声图；

网络模型

虽然通过上面一连串很复杂或者看不懂的公式，其实就是为了得到损失函数，或者要知道 Diffusion Model 的优化目标。简化损失函数后的目标变得更加简单了，主要是训练模型 ϵθ 。但是看了很多文章，其实还停留在复杂的数学公式推导，仍然没有定义 Diffusion Model 的网络模型结构。

在定义网络模型之前呢，再次声明，Diffusion Model 中对模型的唯一要求是输入和输出的数据维度 dims 需要相同。有点意思，看到这句话，估计就会想到类似于 U-Net的模型架构，而不是 VAE 那种 Encoder 和 Decoder 对 Latency sapce 压缩的结构啦。

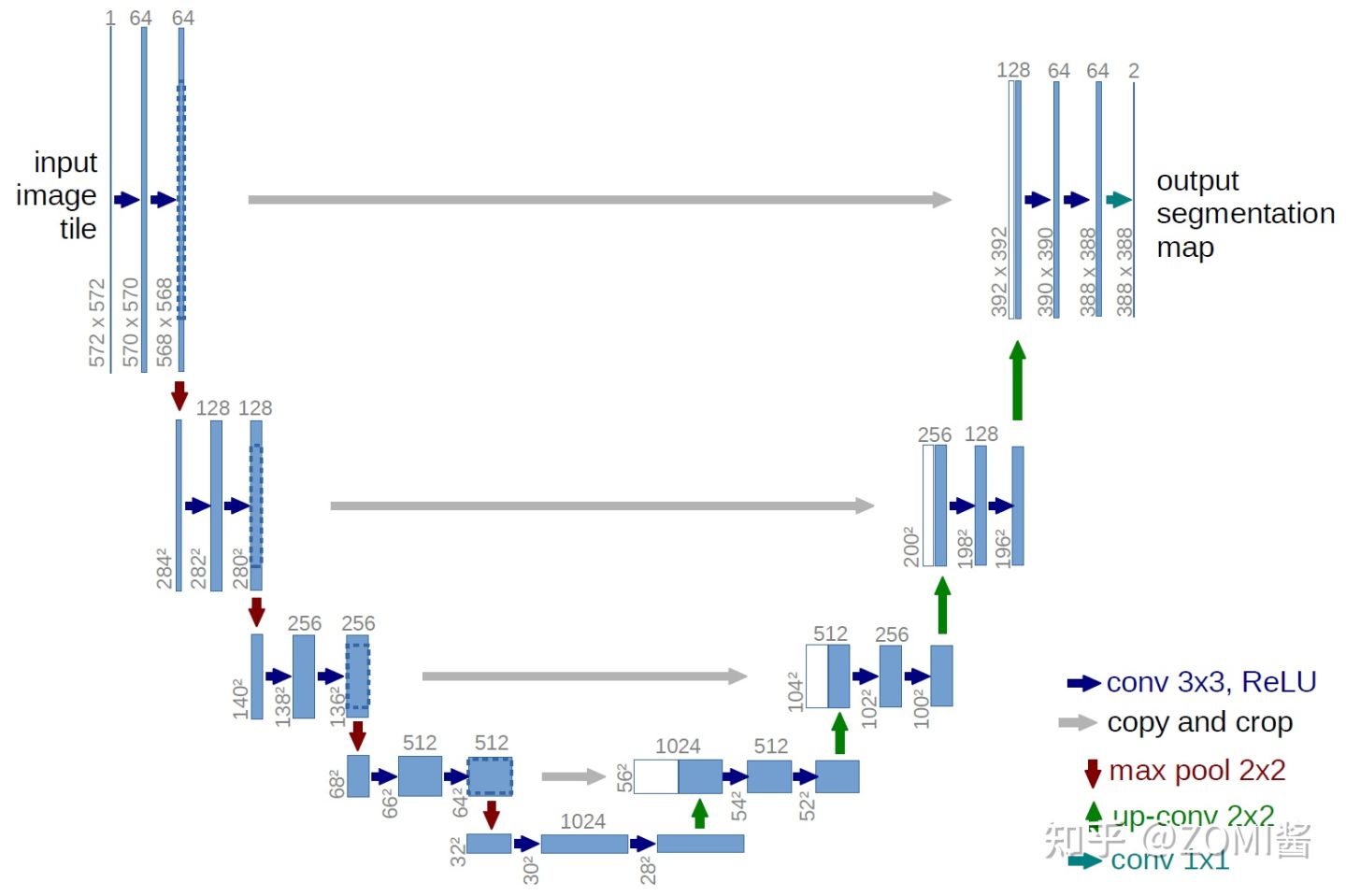
Pytroch 实现

扩散过程

在扩散过程公式（1）中，其中 β1,…,βT 是高斯分布方差的超参数。且实际中 βt 随着 t 增大是递增的，即 β1<…<βT 。在下面实际代码中，我们使用numpy设置 βt 是从 0.0001 到0.02 线性插值linspace，然后再转换称为Pytroch的tensor。对应时间步T，即num_steps设置为1000。

回顾扩散过程的公式(1)：

(1)q(x1:T∣x0):=∏t=1Tq(xt∣xt−1):=∏t=1TN(xt;1−βtxt−1,βtI)

为了方便表达，假设 αt=1−βt ，和 α¯t=∏s=1tαs ，那么有：

(22)q(xt∣x0)=N(xt;α¯txt−1,(1−α¯t)I)

所以代码中 alphas 即对应 αt ，alphas_prod对应 α¯t 。然后先计算得到公式 (22) 中的变量。

num_steps = 1000
beta = torch.tensor(np.linspace(1e-5, 0.2e-2, num_steps))

alphas = 1 - betas
alphas_prod = torch.cumprod(alphas, 0)
alphas_prod_p = torch.cat([torch.tensor([1]).float(), alphas_prod[:-1]], 0)
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)

既然有了公式(22) 中的变量， q(x1:T∣x0) 的函数表示就变得比较简单啦，直接使用下面函数 q_x 来表示。

def q_x(x_0, t, noise=None):
    if not noise: noise = torch.randn_like(x_0)
    alphas_t = extract(alphas_bar_sqrt, t, x_0)
    alphas_1_m_t = extract(one_minus_alphas_bar_sqrt, t, x_0)
    return (alphas_t * x_0 + alphas_1_m_t * noise)

正向过程正式的计算比较简单直接，正如上面理论部分提到的，通过时间步 T 在每次马尔科夫链的转换过程对样本数据 dataset 添加噪声：

for i in range(num_steps):
    q_i = q_x(dataset, torch.tensor([i]))

对应公式求解 q(xt∣x0) 则为：

posterior_mean_coef_1 = (betas * torch.sqrt(alphas_prod_p) / (1 - alphas_prod))
posterior_mean_coef_2 = ((1 - alphas_prod_p) * torch.sqrt(alphas) / (1 - alphas_prod))
posterior_variance = betas * (1 - alphas_prod_p) / (1 - alphas_prod)
posterior_log_variance_clipped = torch.log(torch.cat((posterior_variance[1].view(1, 1), posterior_variance[1:].view(-1, 1)), 0)).view(-1)

def q_posterior_mean_variance(x_0, x_t, t):
    coef_1 = extract(posterior_mean_coef_1, t, x_0)
    coef_2 = extract(posterior_mean_coef_2, t, x_0)
    mean = coef_1 * x_0 + coef_2 * x_t
    var = extract(posterior_log_variance_clipped, t, x_0)
    return mean, var

训练过程

与正向扩散过程不同，逆扩散过程需要训练神经网络模型，这里通过定义损失函数和训练参数，然后进行训练。

损失函数刚才原理部分已经讲过啦，通过最小化数据的负对数似然的变分上限进行求解，也就是对应公式(17)。而网络模型直接使用Unet，这里面就不再展开Unet的编写啦，网上一大堆。

from model import Unet
from ema import EMA
import torch.optim as optim

model = Unet()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

# Create EMA model
ema = EMA(0.9)
ema.register(model)

# Batch size
batch_size = 128
for t in range(num_steps):
    # X is a torch Variable
    permutation = torch.randperm(dataset.size()[0])
    for i in range(0, dataset.size()[0], batch_size):
        # Retrieve current batch
        indices = permutation[i:i+batch_size]
        batch_x = dataset[indices]
        # Compute the loss.
        loss = noise_estimation_loss(model, batch_x, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, num_steps)
        # Before the backward pass, zero all of the network gradients
        optimizer.zero_grad()
        # Backward pass: compute gradient of the loss with respect to parameters
        loss.backward()
        # Perform gradient clipping
        torch.nn.utils.clip_grad_norm_(model.parameters(), 1.)
        # Calling the step function to update the parameters
        optimizer.step()
        # Update the exponential moving average
        ema.update(model)

    # Print loss
    if (t % 100 == 0):
        print(loss)

参考公式(17)的实现损失函数，在上面训练的过程中其实没有展开，下面给出简单的代码示例，有空再详细解读，今天有点肚子痛，赶着收工。

def noise_estimation_loss(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):
    batch_size = x_0.shape[0]
    # Select a random step for each example
    t = torch.randint(0, n_steps, size=(batch_size // 2 + 1,))
    t = torch.cat([t, n_steps - t - 1], dim=0)[:batch_size].long()
    # x0 multiplier
    a = extract(alphas_bar_sqrt, t, x_0)
    # eps multiplier
    am1 = extract(one_minus_alphas_bar_sqrt, t, x_0)
    e = torch.randn_like(x_0)
    # model input
    x = x_0 * a + e * am1
    output = model(x, t)
    return (e - output).square().mean()

最终结果

总结

学习 Diffusion Model 的过程当中，很容易陷入具体的数学细节，像我这样一看到数学就头痛的同学直接劝退，有些喜欢数学的同学则是不能自拔。下面总结一些 Diffusion Model 的要点。

1. Diffusion Model 通过参数化的方式表示为马尔科夫链，这意味着隐变量 x1,…,xT 都满足当前时间步 t 只依赖于上一个时间步 t-1，这样对后续计算很有帮助。
2. 马尔科夫链中的转变概率分布 pθ(xt−1|xt) 服从高斯分布，在正向扩散过程当中高斯分布的参数是直接设定的，而逆向过程中的高斯分布参数是通过学习得到的。
3. Diffusion Model 网络模型扩展性和鲁棒性比较强，可以选择输入和输出维度相同的网络模型，例如类似于UNet的架构，保持网络模型的输入和输出 Tensor dims 相等。
4. Diffusion Model 的目的是对输入数据求极大似然函数，实际表现为通过训练来调整模型参数以最小化数据的负对数似然的变分上限L=Eq(x0)[−log⁡pθ(x0)] 。
5. 在概率分布转换过程中，因为通过马尔科夫假设，目标函数第4点中的变分上限都可以转变为利用 KL 散度来计算，因此避免了采用蒙特卡洛采样的方式。

引用

[1] Deep Unsupervised Learning using Nonequilibrium Thermodynamics

[2] Generative Modeling by Estimating Gradients of the Data Distribution

[3] Denoising Diffusion Probabilistic Models

[4] Improved Techniques for Training Score-Based Generative Models

[5] Improved Denoising Diffusion Probabilistic Models

[6] Diffusion Models Beat GANs on Image Synthesis

[7] GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models

[8] Hierarchical Text-Conditional Image Generation with CLIP Latents

[9] Introduction to Diffusion Models for Machine Learning

[10] diffusion-models-made-easy

[11] denoising-diffusion-model · GitHub