点击关注,桓峰基因
桓峰基因
生物信息分析,SCI文章撰写及生物信息基础知识学习:R语言学习,perl基础编程,linux系统命令,Python遇见更好的你
57篇原创内容
公众号
前言
Calibration curve,直译过来就是校准曲线或校准图。其实,校准曲线就是实际发生率和预测发生率的散点图。实质上,校准图曲线是Hosmer-Lemeshow拟合优度检验的结果可视化。目前校准曲线常用来评价logistic回归和cox回归模型。
校准曲线的算法
步骤1 对预测概率进行分桶(分桶的策略分为’uniform’, ‘quantile’)
步骤2 求出每个桶里面所有样本预测概率的平均值,作为横坐标
步骤3 求出每个桶里面正例的概率,作为纵坐标。
步骤4 将这些点连起来,就成为了校准曲线。
我们在pubmed 中搜索一篇文章,结直肠癌预测临床转移的概率,这篇文章 IF 26分,利用Lasso 回归筛选变量,并且构建模型。

我们看到其中就是分析了模型的校准曲线,可见,模型评估的一些分析在建模类文章中是必不可少的一部分,所以学会了这类文章不用愁,如下:
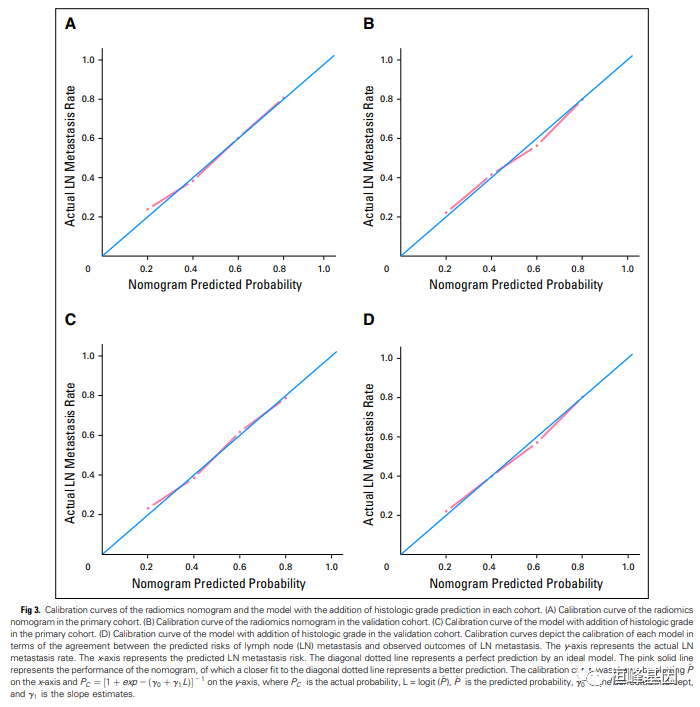
实例解析
Cox 回归在 survival 和 rms 这两个包中都可以实现,我们选择rms程序包里面的函数。加载 survival 和 rms 程序包,如下:
if (!require(survival)) {
install.packages("survival")
}
if (!require("rms")) {
install.packages("rms")
}
if (!require("PredictABEL")) {
install.packages("PredictABEL")
}
## Warning: 程辑包'PredictABEL'是用R版本4.1.3 来建造的
library(survival)
library(rms)
library(PredictABEL)
1.数据读取
我们仍然采用软件包自带的肺癌数据库 NCCTG Lung Cancer Data 作为输入数据,如下:
Descrption
Survival in patients with advanced lung cancer from the North Central Cancer Treatment Group. Performance scores rate how well the patient can perform usual daily activities.
data(package = "survival")
# 2. 打包数据
lung$status <- ifelse(lung$status == 1, 0, 1)
dd <- datadist(lung)
options(datadist = "dd")
head(dd)
## $limits
## inst time status age sex ph.ecog ph.karno pat.karno
## Low:effect 3 166.75 0 56 1 0 75 70
## Adjust to 11 255.50 0 63 1 1 80 80
## High:effect 16 396.50 1 69 2 1 90 90
## Low:prediction 1 31.00 0 44 1 0 60 60
## High:prediction 26 740.00 1 76 2 2 100 100
## Low 1 5.00 0 39 1 0 50 30
## High 33 1022.00 1 82 2 3 100 100
## meal.cal wt.loss
## Low:effect 635.0000 0.00000
## Adjust to 975.0000 7.00000
## High:effect 1150.0000 15.75000
## Low:prediction 312.4361 -5.00000
## High:prediction 1500.0000 35.23348
## Low 96.0000 -24.00000
## High 2600.0000 68.00000
##
## $values
## $values$status
## [1] 0 1
##
## $values$sex
## [1] 1 2
##
## $values$ph.ecog
## [1] 0 1 2 3
##
## $values$ph.karno
## [1] 50 60 70 80 90 100
##
## $values$pat.karno
## [1] 30 40 50 60 70 80 90 100
2.Cox 回归模型构建
使用rms 程序包中的 cph 函数构造Cox 回归模型,其中的几个变量需要根据之前做Cox回归模型时显著的那几个变量,然后做Cox回归,我们发现 sex 和 ph.ecog 两个变量显著性最高,如下:
cph <- cph(Surv(time, status) ~ age + sex + ph.ecog + ph.karno, data = lung, x = TRUE,
y = TRUE, surv = TRUE)
cph
## Frequencies of Missing Values Due to Each Variable
## Surv(time, status) age sex ph.ecog
## 0 0 0 1
## ph.karno
## 1
##
## Cox Proportional Hazards Model
##
## cph(formula = Surv(time, status) ~ age + sex + ph.ecog + ph.karno,
## data = lung, x = TRUE, y = TRUE, surv = TRUE)
##
##
## Model Tests Discrimination
## Indexes
## Obs 226 LR chi2 31.27 R2 0.129
## Events 163 d.f. 4 Dxy 0.263
## Center 1.6323 Pr(> chi2) 0.0000 g 0.550
## Score chi2 31.06 gr 1.732
## Pr(> chi2) 0.0000
##
## Coef S.E. Wald Z Pr(>|Z|)
## age 0.0129 0.0094 1.37 0.1712
## sex -0.5726 0.1692 -3.38 0.0007
## ph.ecog 0.6329 0.1760 3.60 0.0003
## ph.karno 0.0126 0.0095 1.32 0.1870
##
3. 校准曲线绘制
本期选用rms 和 PredictABEL 两个包中的函数进行可视化,比较一下差异,主要目的也是方便大家选择。
1. calibrate {rms}
绘制校准曲线时需要注意以下参数,需要根据自己的数据量情况设置参数,如下:
1、绘制校正曲线前需要在模型函数中添加参数x=T, y=T,详细参考帮助
2、u需要与之前模型中定义好的time.inc一致,即365或730;
3、m要根据样本量来确定,由于标准曲线一般将所有样本分为3组(在图中显示3个点),而m代表每组的样本量数,因此m*3应该等于或近似等于样本量;
4、b代表最大再抽样的样本量
cal <- calibrate(cph, cmethod = "KM", method = "boot", u = 365, m = 38, B = 228)
## Using Cox survival estimates at 120 Days
cal
## calibrate.cph(fit = cph, cmethod = "KM", method = "boot", u = 365,
## m = 38, B = 228)
##
##
## n=226 B=228 u=365 Day
##
## index.orig training test mean.optimism mean.corrected n
## [1,] -0.4836310 -0.002478164 -0.003134677 0.0006565131 -0.4842875 228
## [2,] -0.5180526 0.010037703 -0.058465514 0.0685032169 -0.5865558 28
## [3,] -0.4576156 0.075069139 0.053964406 0.0211047329 -0.4787204 11
## [4,] -0.3499039 NaN NaN NaN NaN 0
## [5,] -0.3336164 NaN NaN NaN NaN 0
## mean.predicted KM KM.corrected std.err
## [1,] 0.7422109 0.2585799 0.2579234 0.2736880
## [2,] 0.8120250 0.2939724 0.2254692 0.2582661
## [3,] 0.8530646 0.3954489 0.3743442 0.1908749
## [4,] 0.8882504 0.5383464 NaN 0.1517891
## [5,] 0.9229901 0.5893736 NaN 0.1466856
plot(cal, lwd = 2, lty = 1, errbar.col = c(rgb(0, 118, 192, maxColorValue = 255)),
xlab = "Nomogram-Predicted Probability of 1-Year OS", ylab = "Actual 1-Year DFS (proportion)",
col = c(rgb(192, 98, 83, maxColorValue = 255)), subtitles = FALSE, xlim = c(0,
1), ylim = c(0, 1), main = "Calibrate plot")
lines(cal[, c("mean.predicted", "KM")], type = "l", lwd = 2, col = c(rgb(192, 98,
83, maxColorValue = 255)), pch = 16)
abline(0, 1, lty = 3, lwd = 2, col = c(rgb(0, 118, 192, maxColorValue = 255)))
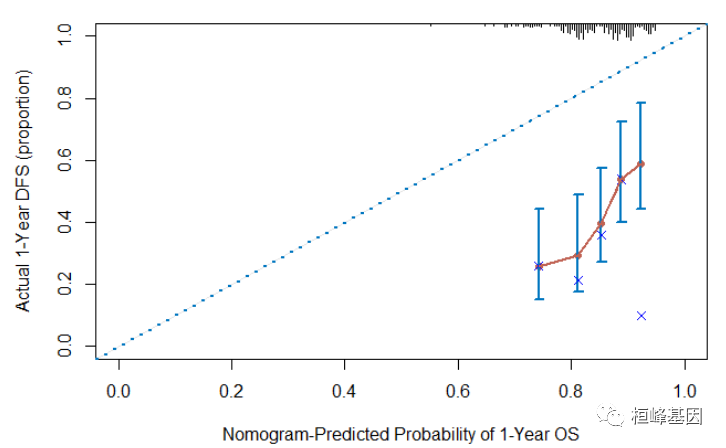
Figure 1:calibrate {rms}
截断坐标轴,我们发现整体放大,但是偏离对角线很多,如下:
cal <- calibrate(cph, cmethod = "KM", method = "boot", u = 365, m = 38, B = 228)
## Using Cox survival estimates at 120 Days
cal
## calibrate.cph(fit = cph, cmethod = "KM", method = "boot", u = 365,
## m = 38, B = 228)
##
##
## n=226 B=228 u=365 Day
##
## index.orig training test mean.optimism mean.corrected n
## [1,] -0.4836310 -0.002476923 -0.003246274 0.0007693507 -0.4844003 228
## [2,] -0.5180526 0.065659393 0.028730528 0.0369288647 -0.5549814 34
## [3,] -0.4576156 0.143006671 0.081213276 0.0617933958 -0.5194090 9
## [4,] -0.3499039 0.118159126 0.114331558 0.0038275678 -0.3537315 1
## [5,] -0.3336164 NaN NaN NaN NaN 0
## mean.predicted KM KM.corrected std.err
## [1,] 0.7422109 0.2585799 0.2578105 0.2736880
## [2,] 0.8120250 0.2939724 0.2570435 0.2582661
## [3,] 0.8530646 0.3954489 0.3336555 0.1908749
## [4,] 0.8882504 0.5383464 0.5345189 0.1517891
## [5,] 0.9229901 0.5893736 NaN 0.1466856
plot(cal, lwd = 2, lty = 1, errbar.col = c(rgb(0, 118, 192, maxColorValue = 255)),
xlab = "Nomogram-Predicted Probability of 1-Year OS", ylab = "Actual 1-Year DFS (proportion)",
col = c(rgb(192, 98, 83, maxColorValue = 255)), subtitles = FALSE, main = "Calibrate plot")
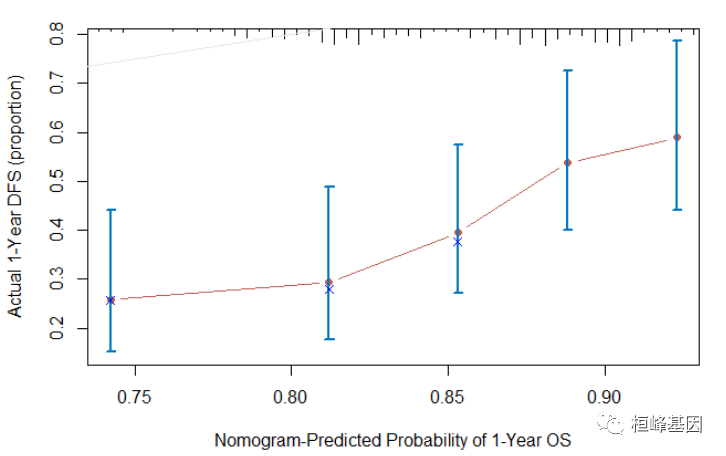
Figure 2:calibrate {rms}
2. plotCalibration {PredictABEL}
这个方式是需要先计算出预测值和真实值,然后用plotCalibration函数绘图,从下图可以看出,数据偏离还是很大的,说明模型的预测能力不够。
newdata <- lung[101:200, ] #用来校准的数据,这里从源数据中调取了部分
pred.lg <- predict(cph, newdata) #每位患者的风险评分
newdata$prob <- 1/(1 + exp(-pred.lg)) #将pred.lg做数据转化,数值更直观
prob <- newdata$prob
plotCalibration(data = newdata, cOutcome = 3, predRisk = prob, groups = 10, plottitle = "Calibration plot") #3为结局指标所在列数
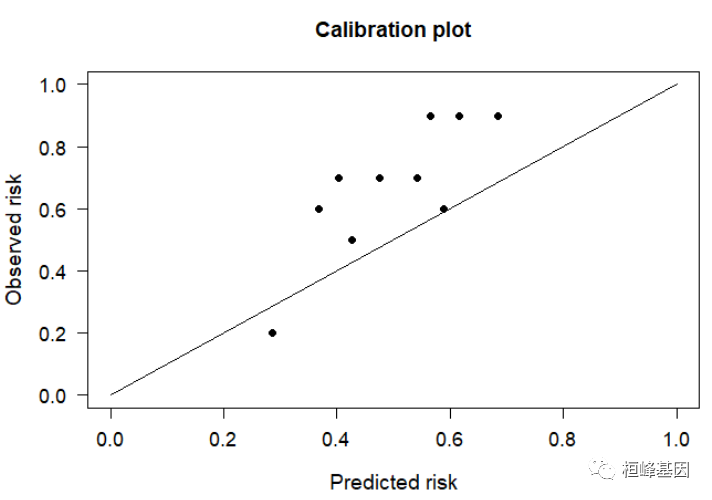
Figure 3:plotCalibration {PredictABEL}
## $Table_HLtest
## total meanpred meanobs predicted observed
## [0.256,0.315) 10 0.285 0.2 2.85 2
## [0.315,0.394) 10 0.367 0.6 3.67 6
## [0.394,0.415) 10 0.403 0.7 4.03 7
## [0.415,0.453) 10 0.427 0.5 4.27 5
## [0.453,0.519) 10 0.476 0.7 4.76 7
## [0.519,0.560) 10 0.541 0.7 5.41 7
## [0.560,0.576) 10 0.566 0.9 5.66 9
## [0.576,0.597) 10 0.588 0.6 5.88 6
## [0.597,0.656) 10 0.616 0.9 6.16 9
## [0.656,0.715] 10 0.684 0.9 6.84 9
##
## $Chi_square
## [1] 19.721
##
## $df
## [1] 8
##
## $p_value
## [1] 0.0114
结果解读
Figure 1: 横坐标为预测的事件发生率(Predicted risk),纵坐标是观察到的实际事件发生率(Observed risk),范围均为0到1,可以理解为事件发生率(百分比)。对角线的虚线是参考线,即预测值=实际值的情况。红线是曲线拟合线,两边带颜色部分是95%CI。
• 如果预测值=观察值,则红线与参考线完全重合
• 如果预测值>观察值,即高估了风险,则红线在参考线下面
• 如果预测值<观察值,即低估了风险,则黑线在参考线上面
Figure 3: 横坐标为预测的事件发生率(Predicted Probablity),纵坐标是观察到的实际事件发生率(Actual Rate),范围均为0到1,可以理解为事件发生率(百分比)。对角线的虚线是参考线,即预测值=实际值的情况。
最理想的情况下, 校准曲线是一条对角线(预测概率等于经验概率),校准曲线不一定会单调递增, 比如, 当分桶的数量比较多时或者分类器比较弱时,通常情况下, Logistic Regression的校准曲线非常贴近于对角线,缺乏自信的模型的校准曲线是sigmoid形的。
校准曲线是一种评价模型的方法,在实际项目中应该是构建好模型,然后评价模型,改善模型,确定最终模型(C-index/ROC/DCA结果表明模型合格),最后对模型进行可视化展示(如森林图、列线图,生存点图等)。
References:
- Harrell FE Jr: Regression Modeling StrategiesWith Applications to Linear Models, Logistic Regres-sion, and Survival Analysis. New York, NY, SpringerVerlag, 2001.
- Hosmer DW, Hosmer T, Le Cessie S, Lemeshow S. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med 1997; 16:965-980.
- Huang YQ, Liang CH, He L, et al. Development and Validation of a Radiomics Nomogram for Preoperative Prediction of Lymph Node Metastasis in Colorectal Cancer. J Clin Oncol. 2016 Jul 10;34(20):2436.
版权归原作者 桓峰基因 所有, 如有侵权,请联系我们删除。