是对之前看过的一些论文内容的整理。以下方法大部分都是几何+深度学习的结合。部分有开源（碎碎念：有时候看不到具体的代码实现真的很苦恼），这里主要是对几何相关的部分做了一个简单的梳理（比较细节，没有什么大局观），理解不一定完全正确。知乎上近期有几篇很好的关于动态SLAM的帖子，没看过的小伙伴不要错过。
一. 基于多分辨率的range image
1. RF-LIO: Removal-First Tightly-coupled Lidar Inertial Odometry in High Dynamic Environments
利用的是多分辨率的range image。使用投影的range image的可见性来进行移动点识别。
1）
F
k
+
1
F_{k+1}
Fk+1是当前关键帧，
M
k
M_k
Mk是对应的子地图，这个子地图是通过
F
k
+
1
F_{k+1}
Fk+1周围的滑窗创建的。考虑到实时性，使用了完整的一个雷达扫描和特征子地图去比较。为什么用特征子地图呢? 因为对应多个关键帧的特征子地图和完整的雷达扫描有着相似的密度，而且特征子地图比完整的子地图点更少。
2）将点云分成两个互斥的子集，动态点集和静态点集。所以上面的关键帧和子地图就可以这么表示：
M
=
M
D
∪
M
S
F
=
F
D
∪
F
S
(
⋅
)
D
∩
(
⋅
)
S
=
∅
M = M^D \cup M^S \space \ \ \ \ \ \ \ \ \ \ \ F = F^D \cup F^S \\ (\cdot)^D \cap (\cdot)^S = \varnothing
M=MD∪MS F=FD∪FS(⋅)D∩(⋅)S=∅
下面这张range image，他的尺寸是由雷达的垂直和水平视角范围以及雷达的分辨率决定的。首先，设定关键帧F或者子地图中的点为某点p，那么这个点的球坐标就表示为
p
i
j
M
o
r
F
p_{ij}^{M or F}
pijMorF, i是球坐标系中的方位角，j是俯仰角。
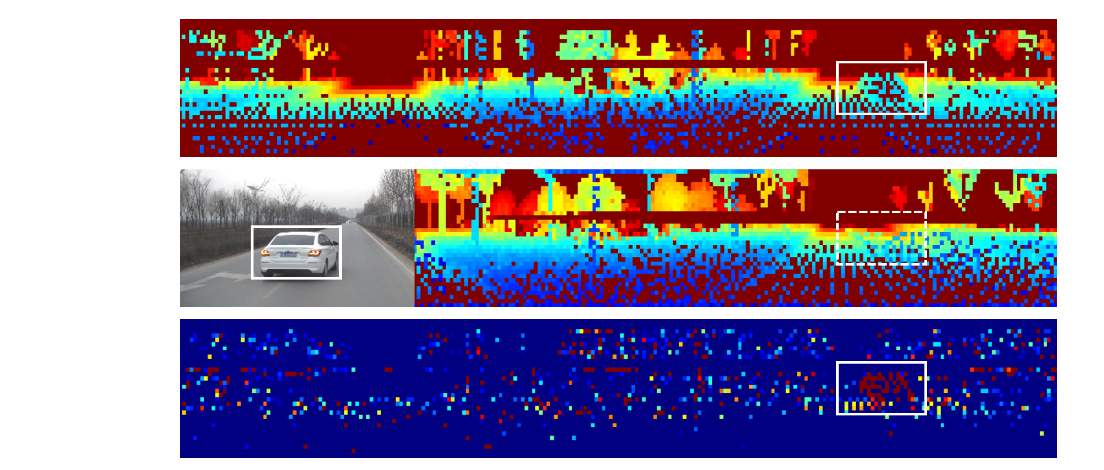
最上面的图是当前帧
I k + 1 F I_{k+1}^F Ik+1F的range image， 中间的图是子地图 I k M I_k^M IkM的range image， 最下面一行是两者的差值 I k + 1 D i f f I_{k+1}^Diff Ik+1Diff。 每个像素点的颜色表示在关键帧K+1时，该像素点对应的3D点到传感器的距离。蓝色表示距离更近，红色代表距离更远，所以最下面的图中红色的像素代表的就是移动的点。
range image中在像素坐标(i,j)处的值表示为
I
k
+
1
,
i
j
I_{k+1,ij}
Ik+1,ij, 这个数值的含义就是点
p
∈
R
3
p \in \mathbb{R}^3
p∈R3到第k+1个关键帧局部坐标系
B
k
+
1
B_{k+1}
Bk+1的距离。
I
k
,
i
j
M
=
min
p
∈
P
i
j
M
d
i
s
t
(
p
)
I
k
+
1
,
i
j
F
=
min
p
∈
P
i
j
F
d
i
s
t
(
p
)
I^M_{k,ij} = \min_{p \in P_{ij}^M} dist(p) \\ I_{k+1,ij}^F = \min_{p \in P^F_{ij}} dist(p)
Ik,ijM=p∈PijMmindist(p)Ik+1,ijF=p∈PijFmindist(p)
上面的公式中，
P
i
j
M
o
r
F
P^{M or F}_{ij}
PijMorF是点集
P
M
o
r
F
P^{M or F}
PMorF的球坐标。
接下来，子地图点和扫描点的可见度就用矩阵元素的减法来计算：
I
k
+
1
D
i
f
f
=
I
k
+
1
F
−
I
k
M
I_{k+1}^{Diff} = I_{k+1}^F - I_k^M
Ik+1Diff=Ik+1F−IkM
如果矩阵
I
k
+
1
,
i
j
D
i
f
f
I_{k+1,ij}^{Diff}
Ik+1,ijDiff中对应的某一个像素点的数值大于一个自适应阈值
τ
\tau
τ, 那么这个点就是动态的。最终，这个点会被定义为：
M
k
D
=
{
M
k
∣
I
k
+
1
D
i
f
f
>
τ
}
F
k
+
1
D
=
{
F
k
+
1
∣
I
k
+
1
D
i
f
f
<
−
τ
}
τ
=
γ
d
i
s
t
(
p
)
M_k^D = \{M_k | I_{k+1}^{Diff} \gt {\tau} \} \\ F_{k+1}^D = \{ F_{k+1} | I_{k+1}^{Diff} \lt - \tau \} \\ \tau = \gamma dist(p)
MkD={Mk∣Ik+1Diff>τ}Fk+1D={Fk+1∣Ik+1Diff<−τ}τ=γdist(p)
γ
\gamma
γ是关于点距离的敏感度，建议把它设置成最终分辨率的最大值，这样可以有效的避免由于错误的分辨率预测而把静态点当成动态点。
分辨率的选取：
r
=
α
δ
p
+
δ
θ
r
f
=
m
a
x
(
β
r
,
r
0
)
r = \alpha \delta p + \delta \theta \\ r_f = max(\beta_{r}, r_0)
r=αδp+δθrf=max(βr,r0)
α
\alpha
α是一个0到1之间的数字，用来给分辨率的平移误差和角度误差来加权（这个算出来的r就是一个分辨率的预测值），为了实时性，移除的比率，以及减小错误预测值的影响，这里还引入了
r
0
r_0
r0,
r
0
=
v
e
r
t
i
c
a
l
F
O
V
v
e
r
t
i
c
a
l
r
a
y
s
r_0 = \frac{vertical FOV}{vertical rays}
r0=verticalraysverticalFOV, 可以防止在range image中有空的像素点。
为什么叫做自适应分辨率的方法呢？
因为如果在后续的帧与子地图的特征点配准中，算出的score没有达到收敛的要求，那么就会在目前位姿误差的基础上再生成一个新的分辨率。然后再把去除动态点的流程都走一遍。
具体的参数设置：
缺点： 不能够移除所有的移动物体。原因涉及到下面两个：
- 有些移动的点离地面太近了(<0.5)，这个距离小于设置的阈值；
- 有一些点是由于平行于地面的激光线束产生的，在子地图中很难找到对应的远点去移除它们（因为后续配准的过程中会舍掉一些远点）
2. Remove, then Revert: Static Point cloud Map Construction using Multi-resolution Range Images
重构问题：
把目标地图分为两种互斥的子集，静态点和动态点。静态状态设为Positive(P), 动态状态设为Negative(N)，任务就是要对地图中的点进行估计，估计结果如下表示：
P
^
S
M
=
T
P
∪
F
P
P
^
D
M
=
T
N
∪
F
N
\hat{P}^{SM} = TP \cup FP \ \ \ \ \ \hat{P}^{DM} = TN \cup FN
P^SM=TP∪FP P^DM=TN∪FN
要尽可能的减少FP和FN的数量。
方法雏形：
把所有的点都假定为动态点，那么这些点一定是一部分属于TN，一部分属于FN（应该被分为静态点的点），所以就要把这些FN中的点再移动到静态点的集合中。这个过程会被重复的进行直到预测出的地图收敛到近似于真实的静态地图。
I
k
D
i
f
f
=
I
k
Q
−
I
k
M
I_k^{Diff} = I_k^Q - I_k^M \\
IkDiff=IkQ−IkM
使用一个自适应阈值来调节算法对点的距离的敏感性。
τ
D
a
d
a
p
=
r
(
p
i
j
M
)
τ
D
\tau_{D_{adap}} = r(p^M_{ij}) \tau_D
τDadap=r(pijM)τD
升级1：批量动态点的移除
对于建图的工作，不需要考虑到那么强的实时性，所以可以将上面的步骤升级成批量的版本：
具体方法：
- 已知N帧图像，和他们对应的点云地图，按照前面的方法，用每一个单独的帧都对地图点进行动态点的检测。也就是说，我们可以得到N组地图点分类的结果。
- 对于点云地图对应的每一个点，都统计一下它在N组结果中被分类为动态点和静态点的次数，分别用 n D M n_{DM} nDM和 n S M n_{SM} nSM 表示。 如果地图中有的点在整个批量处理过程中没有被标记过，就默认它为静态点。
- 用一个打分来判断最终这个地图点到底属于哪种状态。对于某一个地图点，如果得分 s : = α S M n S M + α D M n D M s := \alpha_{SM} n_{SM} + \alpha_{DM} n_{DM} s:=αSMnSM+αDMnDM，小于定义的阈值 τ S \tau_S τS, 那么就被判断为动态点。
参数设置：
α
S
M
=
0.3
α
D
M
=
−
0.7
τ
D
=
0.01
τ
S
=
−
0.1
\alpha_{SM} = 0.3 \\ \alpha_{DM} = -0.7 \\ \tau_D = 0.01 \\ \tau_S= -0.1
αSM=0.3αDM=−0.7τD=0.01τS=−0.1
优点：
- 可以克服地图点遮挡带来的问题
- 解决单独一帧有限的FOV带来的局限
- 如果我们就按照运动序列的顺序进行某些帧的采样，那么就会难以移除在车前方的以相同速度运动的物体。所以，在选择这一批单独的帧时，采用了随机的选择。
升级2：Removert加入多分辨率的range image
前一种方法还存在的问题：
估计出来的动态点中会包含一些静态点，比如可能会移除掉一些在物体边缘或者在地面的点，所以需要再进行其他处理。
比如：即使地面点的入射角差异很小，它们的范围变化很大，这样一个静态的地面点很容易被误认为是动态的。
思路：
如果一个地图点在精细的分辨率下被分为动态点（Remove），而在更粗糙的分辨率下被分为静态点，那么这个点最终就被分为静态点（Revert）。根据作者论文所说，虽然也会有一部分“真的动态点”被归为静态，但大多数还是成功的从原来动态点中给揪出来的静态点。
注意：如果range image的分辨率太粗糙，那么一些靠近地面的点就可能会被错误的恢复成静态点。
二. 对深度图进行聚类
论文Improving RGB-D SLAM in dynamic environments: A motion removal approach
这篇论文很早期了，其中也有聚类的思想
论文Towards Real-time Semantic RGB-D SLAM in Dynamic Environments
暂时没有找到开源代码，不过思路很好理解，之前也按照文中提到的方式实现了一个简单的聚类效果，不过没有仔细研究对应设备下的耗时。
三. 多视图几何+区域增长(RGB-D)
1.DynaSLAM: Tracking, Mapping and Inpainting in Dynamic Scenes
详细的论文笔记点击这里。
四. 光流金字塔+极线约束
1. DS-SLAM
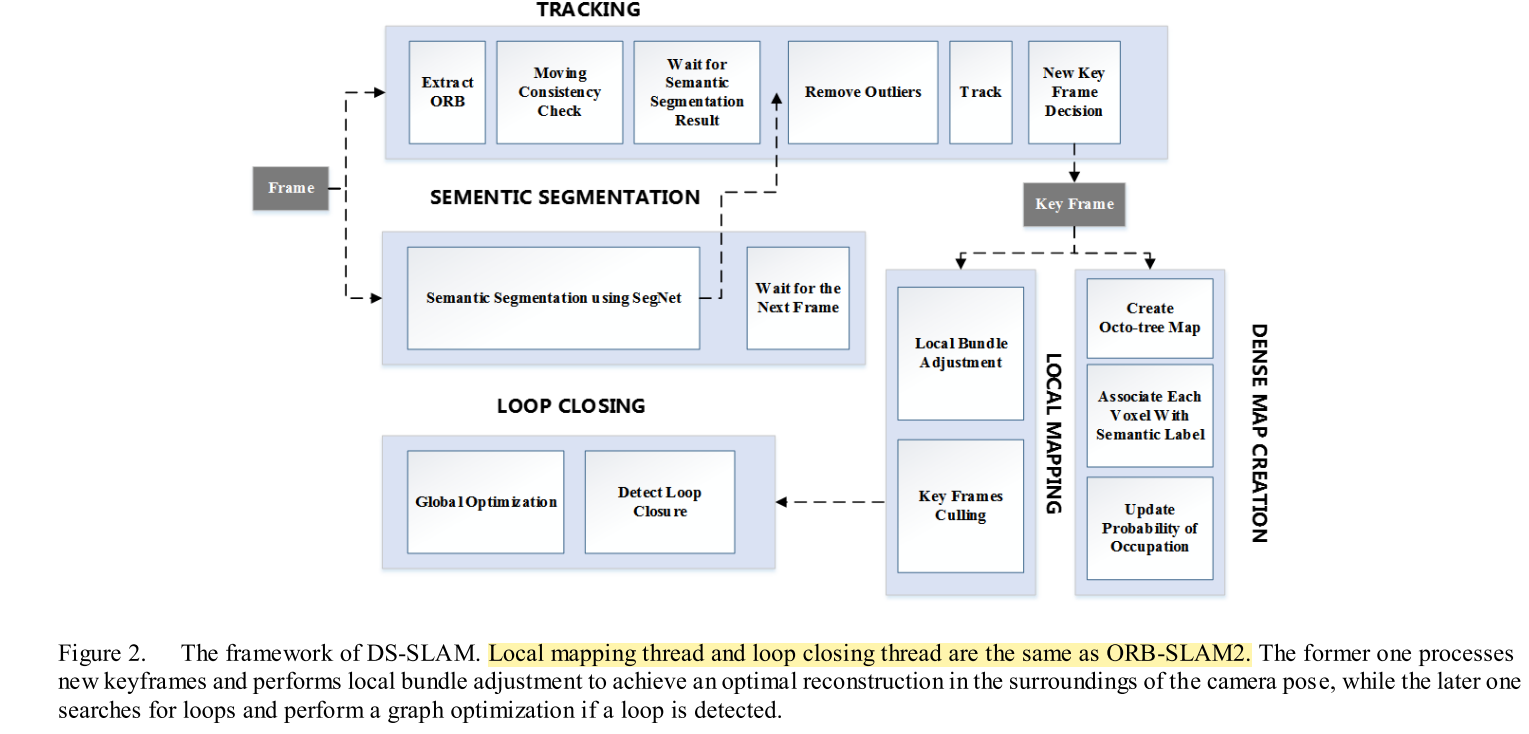
对应于论文的Moving Consistency Check内容。
从动态点->动态物体：
经过语义分割的模块后，可以得到一个分割的Mask的，所以现在的任务就是去确定，某个关键点是否是移动的，如果有一定数量的移动点落在了某一个分割出来的物体轮廓内部，那这个物体就被视为动态，上面所有的特征点都会被剔除。
判断动态点的步骤：
1）计算光流金字塔来得到当前帧中已经匹配的特征点
2）如果匹配点对离图像的边缘太近，或者各自以两个相匹配的点为中心，其3X3区域范围内像素值差异太大，这个匹配点对就会被丢弃
3）使用RANSAC的方法（使用最多内点）找到基础矩阵F
4）使用基础矩阵计算当前帧的极线，已知上一帧中的特征点像素位置为
p
1
=
[
u
1
,
v
1
,
1
]
p_1=[u_1, v_1, 1]
p1=[u1,v1,1], 这个点在当前帧中对应的位置为
p
2
=
[
u
2
,
v
2
,
1
]
p_2=[u_2, v_2, 1]
p2=[u2,v2,1]，然后就可以求出点
p
1
p_1
p1投影到当前帧中的极线
I
1
I_1
I1：
I
1
=
(
X
Y
Z
)
=
F
P
1
=
F
(
u
1
v
1
1
)
I_1= \left( \begin{array}{ccc} X \\ Y \\ Z \end{array}\right) = FP_1 = F \left( \begin{array}{ccc} u_1 \\v_1 \\ 1 \end{array}\right)
I1=⎝⎛XYZ⎠⎞=FP1=F⎝⎛u1v11⎠⎞
5）计算匹配的特征点到它对应极线的距离，如果这个距离超过阈值则被视为移动点，反之为静态点。距离的计算方法如下(就是简单的二维平面中点到直线的距离公式)：
D
=
∣
P
2
T
F
P
1
∣
∣
∣
X
∣
∣
2
+
∣
∣
Y
∣
∣
2
D = \frac{| P_2^T F P_1 |}{\sqrt{ ||X||^2 + ||Y||^2}}
D=∣∣X∣∣2+∣∣Y∣∣2∣P2TFP1∣
当时看论文到这里，有一个比较直接的想法，如果动态物体是沿着极线方向运动，这种方法感觉就失效了，因为只考虑了极线垂直方向距离差值的影响。
关于这一种方法，在一博主的这篇博文中有一个很好的总结，强烈建议阅读，动态场景下基于实例分割的SLAM（总结与反思）。其中还提到了对于不同场景，距离阈值需要再调整的问题，这就提醒了一下要考虑到方法的普适性。
五. 建立概率模型
1. Accurate Dynamic SLAM using CRF-based Long-term Consistency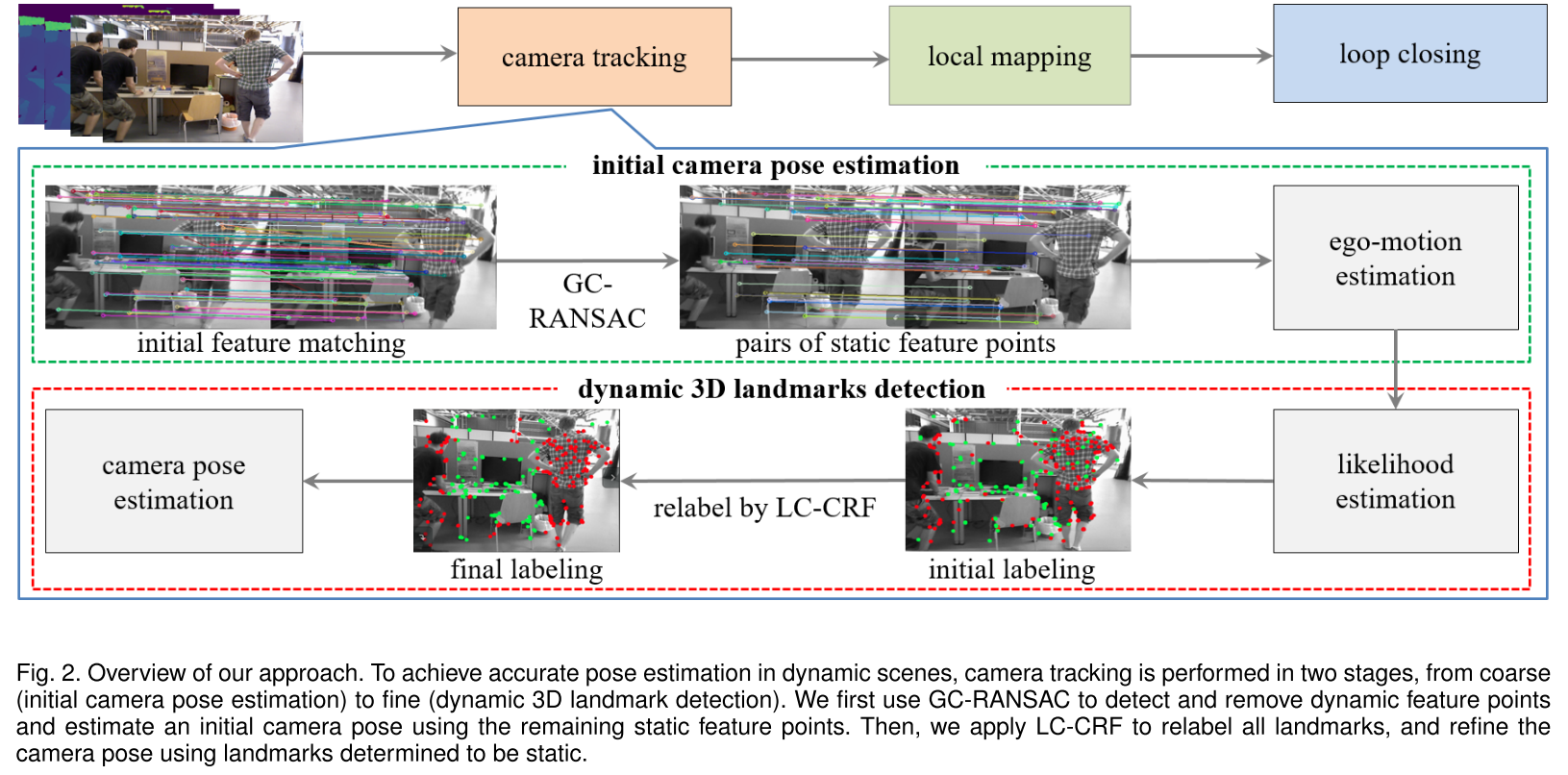
主要是对ORBSLAM2的Tracking部分进行了修改，来检测动态点。方法分为两步，由粗到细，先估计初始相机位姿(GC-RANSAC)，再进行动态3D路标点的检测(LC-CRF)。
初始位姿估计
在ORB中为了求相邻帧之间的位姿是通过求解3D-2D的PnP问题，但对于动态场景，3D-2D的数据关联会因为移动物体而产生误匹配。所以希望的是，只使用静态点来估计相机位姿。
已知当前帧
f
r
f_r
fr，参考帧
f
r
f_r
fr，上一帧
f
l
f_l
fl，要求的是当前帧相机位姿，每一个3D路标点
P
i
P_i
Pi的静态似然值
P
i
γ
P_i^{\gamma}
Piγ。
步骤：
- 先把当前帧和参考帧的特征点进行匹配，可以得到若干匹配点对。
- 使用GC-RANSAC的方法找到静态特征点。这里是把动态点识别的问题构建成了一个外点识别的问题(静态点是内点)，当用GC-RANSAC的方法来估计基础矩阵时，最终确定的外点就会被当做动态点。在RANSAC的每一次迭代中，都会把匹配点对标记为内点或者外点，从而来估计基础矩阵。RANSAC的结果是通过优化下面这个能量函数：( λ = 0.14 \lambda=0.14 λ=0.14, G代表neighbor Graph？？？) E ( L ) = ∑ i B ( L i ) + λ ∑ ( i , j ) ∈ G R ( L i , L j ) E(L) = \sum_i B(L_i) + \lambda \sum_{(i,j)\in G}R(L_i, L_j) E(L)=i∑B(Li)+λ(i,j)∈G∑R(Li,Lj) L i L_i Li表示每个特征点对所对应的标记，1表示外点，0为内点。对于 B ( L i ) B(L_i) B(Li)就有： ( ϵ = 0.1 \epsilon=0.1 ϵ=0.1， ϕ \phi ϕ是匹配点对到基础矩阵的距离， θ \theta θ是基础矩阵的角度参数) B ( L i ) = { K ( ϕ ( p i , p i ′ , θ ) , ϵ ) i f L i = 0 1 − K ( ϕ ( p i , p i ′ , θ ) , ϵ ) i f L i = 1 B(L_i) =\left{\begin{aligned} K(\phi(p_i, p_i^{'}, \theta), \epsilon) && if \ L_i =0\ 1 - K(\phi(p_i, p_i^{'}, \theta), \epsilon) && if \ L_i =1\end{aligned}\right. B(Li)={K(ϕ(pi,pi′,θ),ϵ)1−K(ϕ(pi,pi′,θ),ϵ)if Li=0if Li=1 K ( σ , ϵ ) = e x p ( − σ 2 / ( 2 ϵ 2 ) ) K(\sigma, \epsilon) = exp(-\sigma^2 / (2\epsilon^2)) K(σ,ϵ)=exp(−σ2/(2ϵ2)) R ( L i , L − j ) = { 1 i f L i ≠ L j ( B ( L i ) + B ( L j ) ) / 2 i f L i = L j = 0 1 − ( B ( L i ) + B ( L j ) ) / 2 i f L i = L j = 1 R(L_i, L-j) = \left{\begin{aligned} 1 &&if L_i \neq L_j \ (B(L_i) + B(L_j)) / 2 && if L_i = L_j = 0 \ 1 - (B(L_i) + B(L_j)) / 2 && if L_i = L_j =1 \end{aligned}\right. R(Li,L−j)=⎩⎨⎧1(B(Li)+B(Lj))/21−(B(Li)+B(Lj))/2ifLi=LjifLi=Lj=0ifLi=Lj=1
这里的Lj是什么？ 这个能量方程和RANSAC有什么关系。这个R是什么意思？
3. 对于当前帧的每一个静态特征点，都找到它在参考帧中的3D点
P
i
P_i
Pi
使用PnP和静态点来估计一个位姿
T cT_c
Tc
把上一帧中的所有地图点都投影到当前帧
使用GC-RANSAC来估计当前帧和上一帧的基础矩阵F
对于当前帧和上一帧的每一对特征点对，分别计算对应帧中的极线以及特征点到极线的距离，然后利用距离值来计算静态点/动态点先验概率(对于3D路标点)：
P i γ = e x p ( − ( ( d i + d i ′ ) / 2 − μ γ ) 2 / ( 2 σ γ 2 ) ) P_i^{\gamma} = exp(-((d_i + d_i^{'})/2 - \mu_{\gamma})^2 / (2 \sigma_{\gamma}^2))Piγ=exp(−((di+di′)/2−μγ)2/(2σγ2)) 如果是静态点，到极线的距离就应该很小，
通过CRF进行动态点检测
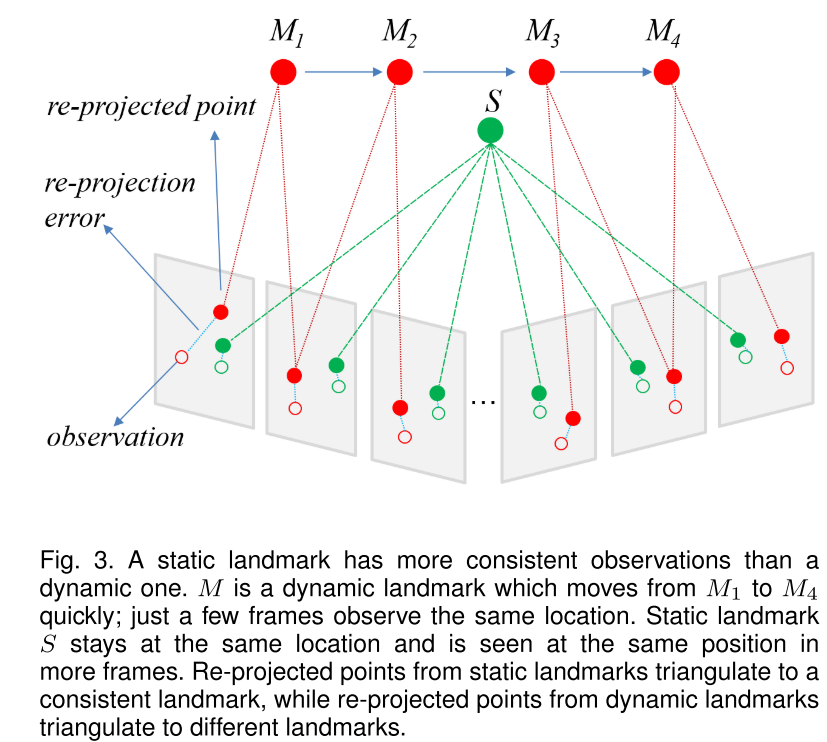使用长时间一致随机场(LC-CRF)的前提假设：
- 一段时间内，动态点有更多的不一致的观测。
- 动态点往往有更大的在重投影点和观测点之间的光度重投影误差
- 静态点周围倾向于是静态点，动态点周围也倾向于是动态点.
通过最小化LC-CRF中的Gibbs energy E来找到所有地图点的优化后的标签。
对于每个3D点，得到它在关键帧中的所有观测位置，然后计算这些点和重投影点之间的光度重投影误差，对一个3D点和其对应的若干个光度误差计算出一个平均误差，由这个误差可以引申出一个静态似然的概率。 第二个误差是什么？？？观测到的点数？？
observation kernel：静态点和动态点之间： 他们的观测数量和平均重投影误差会有显著的不同。
location kernel：静态点周围倾向于是静态点，动态点周围也倾向于是动态点. 如果有静态点周围都是动态点，那就会把它改为动态点
2. RGB-D SLAM in Dynamic Environments Using Static Point Weighting
这里只记录论文中的Static weight estimation部分。
为了估计静态权重，需要一个源点云和一个目标点云，并且只对前景深度边缘点进行静态权重的估计。比如说我们要估计**源点云中某个点
i
i
i的静态权重**
w
i
s
r
c
,
t
g
t
w_i^{src,tgt}
wisrc,tgt，需要计算源点云中点
i
s
r
c
i_{src}
isrc投影到目标点云坐标系后的
i
s
r
c
′
i^{'}_{src}
isrc′，和
i
t
g
t
i_{tgt}
itgt之间的欧氏距离，如果没有在目标点云找到对应的点，就会把这个距离设置为一个较大的常数。
这里做了一个假设， 如果是静态点，那么投影后的点位置应该和观测位置重合，考虑到传感器误差，欧氏距离应该非常小或为0。借助这一特点，以及t分布（Student’s t-distribution）就可以构建出静态权重：
w
i
s
r
c
,
t
g
t
=
v
0
+
1
v
0
+
(
(
d
i
−
μ
D
)
/
σ
D
)
2
w_i^{src,tgt} = \frac{v_0 +1}{v_0 + ((d_i - \mu_D) / \sigma_D)^2}
wisrc,tgt=v0+((di−μD)/σD)2v0+1
这里的
σ
D
=
1.4826
M
e
d
i
a
n
{
∣
d
i
−
μ
D
∣
}
d
i
≠
D
\sigma_D = 1.4826 Median \{ |d_i - \mu_D| \}_{d_i \neq D}
σD=1.4826Median{∣di−μD∣}di=D。
v
0
v_0
v0是t-分布的自由度，本文设置为10，这个**自由度越大**，那么就会导致“随着欧氏距离增大，权重值下降**越快**”。对于没有近邻匹配的点，不会把它考虑进标准差的求解中来（就是欧氏距离被设置为了常数值的那些点）。D的均值被设置为0，因为对于静态点，这个距离会非常小。
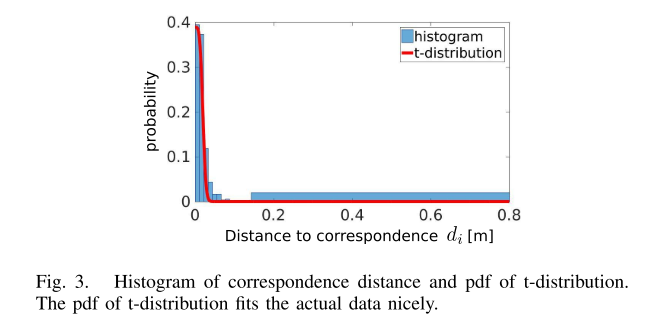从上面这张图，对于那些欧氏距离比较大的点，它成为静态点的概率就会很低。
在论文中，只对关键帧进行静态权重的估计，并把这个关键帧设为源点云。假设我们要求的是最新的关键帧
P
k
P_k
Pk中点的静态权重，那么还需要一个之前的关键帧
P
k
−
N
P_{k-N}
Pk−N和一个当前帧
P
t
P_t
Pt。那么，对于
P
k
P_k
Pk中的点，它对应的权重就可以这么求：
w
S
(
i
)
=
α
w
i
k
,
k
−
N
+
(
1
−
α
)
w
i
k
,
t
w_S(i) = \alpha w_i^{k,k-N} + (1 - \alpha) w_i^{k,t}
wS(i)=αwik,k−N+(1−α)wik,t
w
i
k
,
k
−
N
w_i^{k,k-N}
wik,k−N是以
P
k
P_k
Pk为源点云，把它向
P
k
−
N
P_{k-N}
Pk−N所在坐标系投影求出来的；
w
i
k
,
t
w_i^{k,t}
wik,t也同理，以
P
k
P_k
Pk为源点云。公式中
α
\alpha
α的取值方法如下：
α
=
{
1
i
f
t
=
k
0.5
N
/
(
N
+
t
−
k
)
o
t
h
e
r
w
i
s
e
\alpha =\left\{\begin{aligned} 1 && if\ t=k\\ 0.5N/(N+t-k) && otherwise\end{aligned}\right.
α={10.5N/(N+t−k)if t=kotherwise
论文中称
w
i
k
,
k
−
N
w_i^{k,k-N}
wik,k−N为
初始项
，
w
i
k
,
t
w_i^{k,t}
wik,t为
更新项
。这两项有互补的作用：
- 初始项： 当取的最新一帧就是最新的关键帧时，即t=k时，式子就只剩下第一部分了。如果用这一项，动态物体运动要是很慢，也可以检测，因为这两帧之间时间差更大。
- 更新项： 随时间累积，会更多的去考虑当前帧的影响，因为可能有的点在前面的关键帧 P k P_k Pk和 P k − N P_{k-N} Pk−N是静态的，但在最新一帧中开始运动了。如果只用初始化项，新的动态点就要在关键帧 P k + N P_{k+N} Pk+N才能被检测到，那么在k+1到k+N-1的区间内就会有漂移问题。同时，使用
更新项还有一个好处，前景物体会会有遮挡问题，这就难免 P t P_t Pt中的被遮挡的部分也被引入点云匹配（可以和 P k P_k Pk点云的点配上，但实际不是同一个特征），这时使用更新项，就可以降低这个点的权重，因为遮挡问题通常会使得 d i d_i di很大。
3. Detect SLAM
为了提高整个动态SLAM系统的帧率，采取了两个策略：
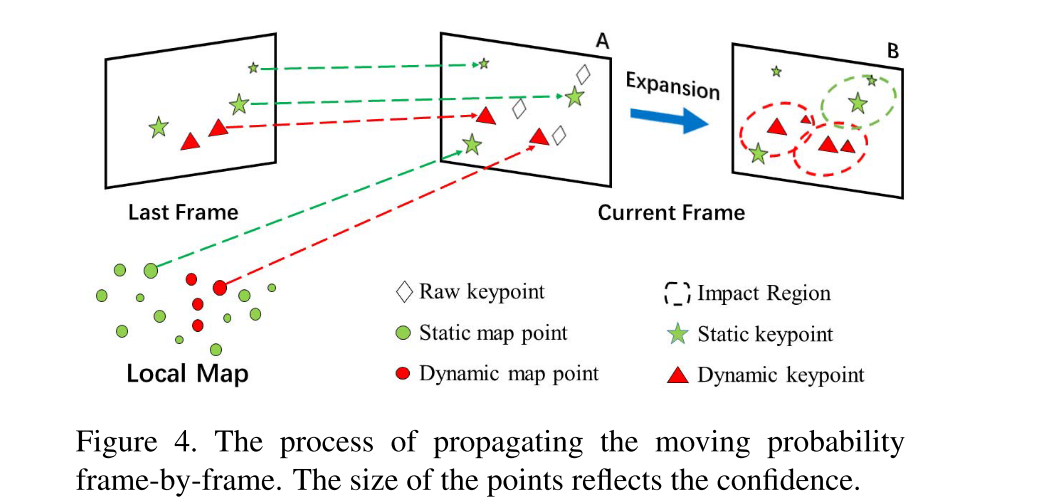
1）只在关键帧检测移动物体，然后更新局部地图中的点的移动概率，从而加速Tracking线程
2）在Tracking线程中，通过特征匹配和匹配点扩张来传播移动概率，从而在进行相机位姿估计之前就可以移除动态物体上的特征点。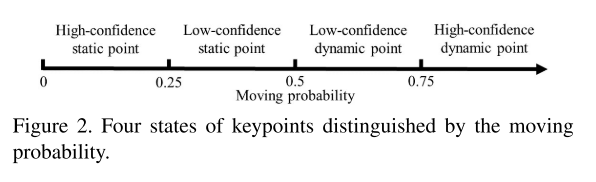
作者引入了移动概率的概念，对于一个特征点，可以分为四种情况。只有在移动概率>0.75时，才能用这个匹配特征点来传递移动概率给周围未完成匹配的点。
当每个点都通过传播得到了移动概率后，移除所有动态点，并用RANSAC的方法去除其他外点，对位姿进行估计。
更新移动概率：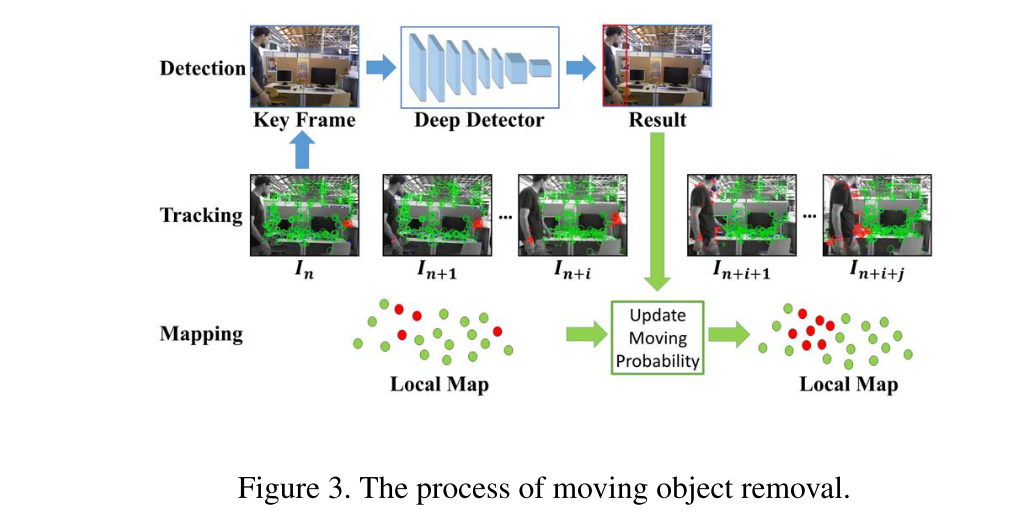
一边对关键帧进行检测的同时，也在Tracking线程中传播移动概率。一旦有了检测结果，就把关键帧加入局部地图，并更新局部地图中的移动概率。
用下面的式子来更新能和关键帧特征点匹配的3D点：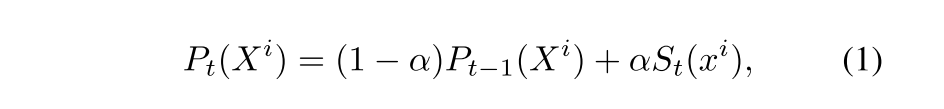
等号右边第一项概率是更新上一关键帧
I
t
−
1
I_{t-1}
It−1后，3D点
X
i
X^i
Xi的移动概率。如果这是新的地图点，那么就把这个概率初始化为0.5， 后面那一项表示的是匹配的特征点
x
i
x^i
xi在**关键帧**
I
t
I_t
It中的状态。如果
x
i
x^i
xi落在了动态物体的检测框里，那么S值就被设置为1，否则视为0（静态）。权重
α
=
0.3
\alpha = 0.3
α=0.3，这个值越大表明越相信当前关键帧的检测结果，越小表示越相信之前多视角得来的概率，取0.3是因为作者发现在复杂环境中，检测结果有时会有错误。
移动概率传播
在Tracking线程中，会给每一帧的每一个关键点都做移动概率的估计：
1）特征匹配：如果当前帧的特征点
x
t
i
x_t^i
xti和上一帧的某个关键点
x
t
−
1
i
x_{t-1}^i
xt−1i匹配，那么移动概率
P
t
(
x
t
−
1
i
)
P_t(x_{t-1}^i)
Pt(xt−1i)就可以被传播。如果一个特征点可以和局部地图中的3D点
X
t
i
X_t^i
Xti匹配，那么它的移动概率就为
P
(
X
t
i
)
P(X_t^i)
P(Xti)。如果一个特征点和上一帧以及局部地图都匹配了，那么优先局部地图的概率，而对于剩下的都没有匹配上的特征点，把他们的概率设置为0.5.
2）匹配点扩张：
这里有一个假设，相邻点的状态在多数情况下是一样的。
在完成了1）之后，还可以采取一些补救措施，把1）中那些高置信度的点（很可能是动态或很可能是静态），以它为中心取一个半径为r的圆形区域，如果区域内有未匹配的点，就可以更新这些点的概率：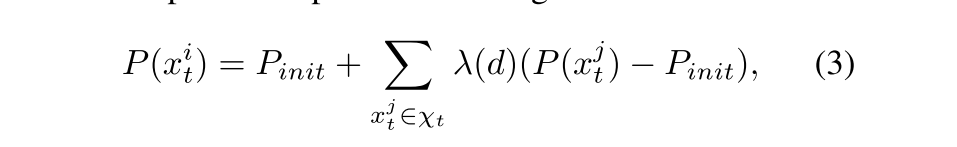
如果未匹配的点在圆形区域内，这里的
λ
(
d
)
=
C
∗
e
−
d
r
\lambda(d)= C*e^{-\frac{d}{r}}
λ(d)=C∗e−rd，是一个距离系数，
4. RGB-D SLAM in Dynamic Environments Using Point Correlations
一个纯几何的方法。有一个强假设是：环境中的静态点要多于动态点。这个方法比较不一样的点是工作的大头是在后端优化部分的。建议感兴趣的直接看原文~
版权归原作者 wrotcat 所有， 如有侵权，请联系我们删除。