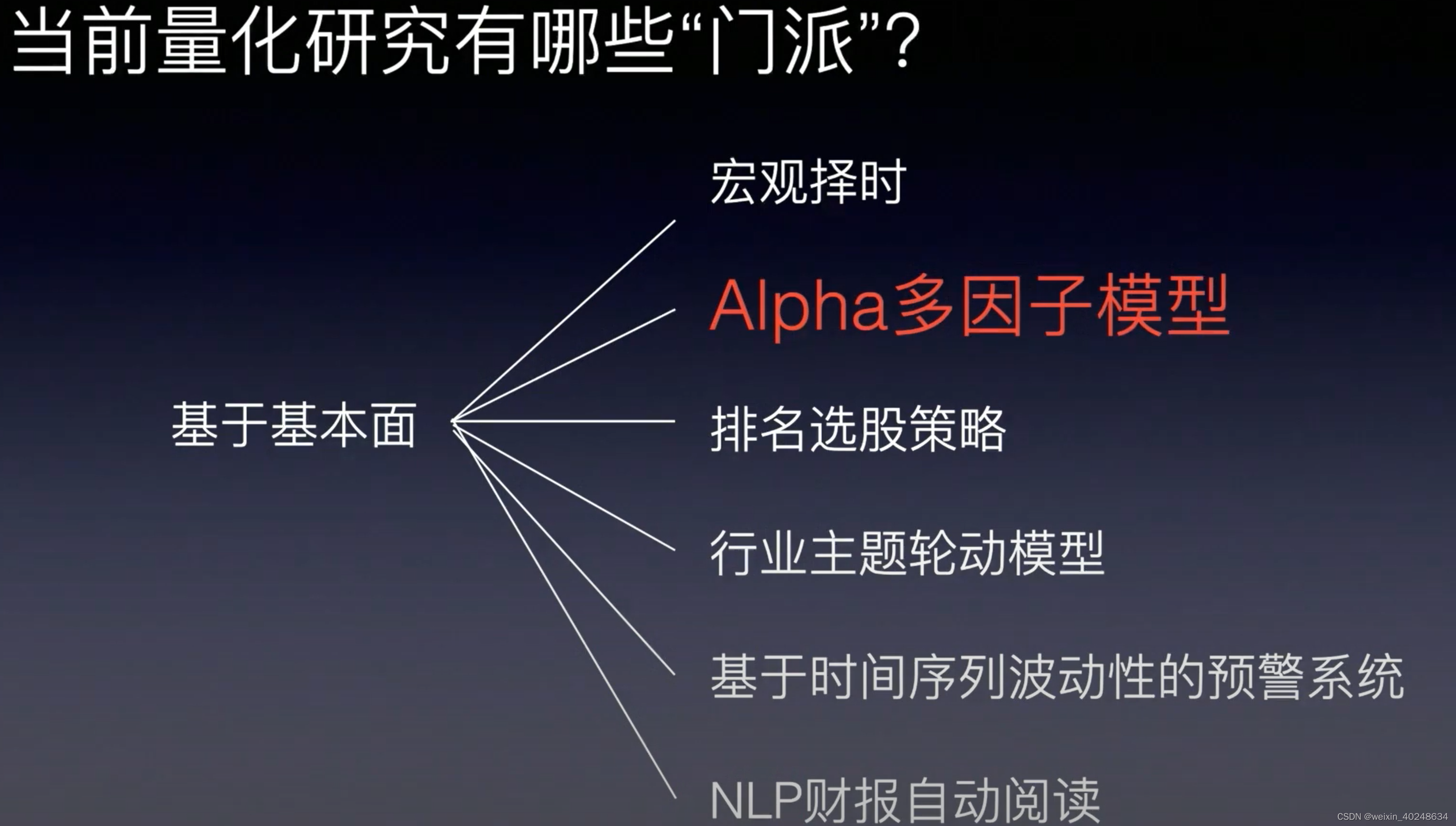
CAPM & APT & FF三因子模型
因子投资基础
CAPM (资本资产定价模型)
横轴为风险（标准差sigma），纵轴为预期收益。
风险越高，收益就越高
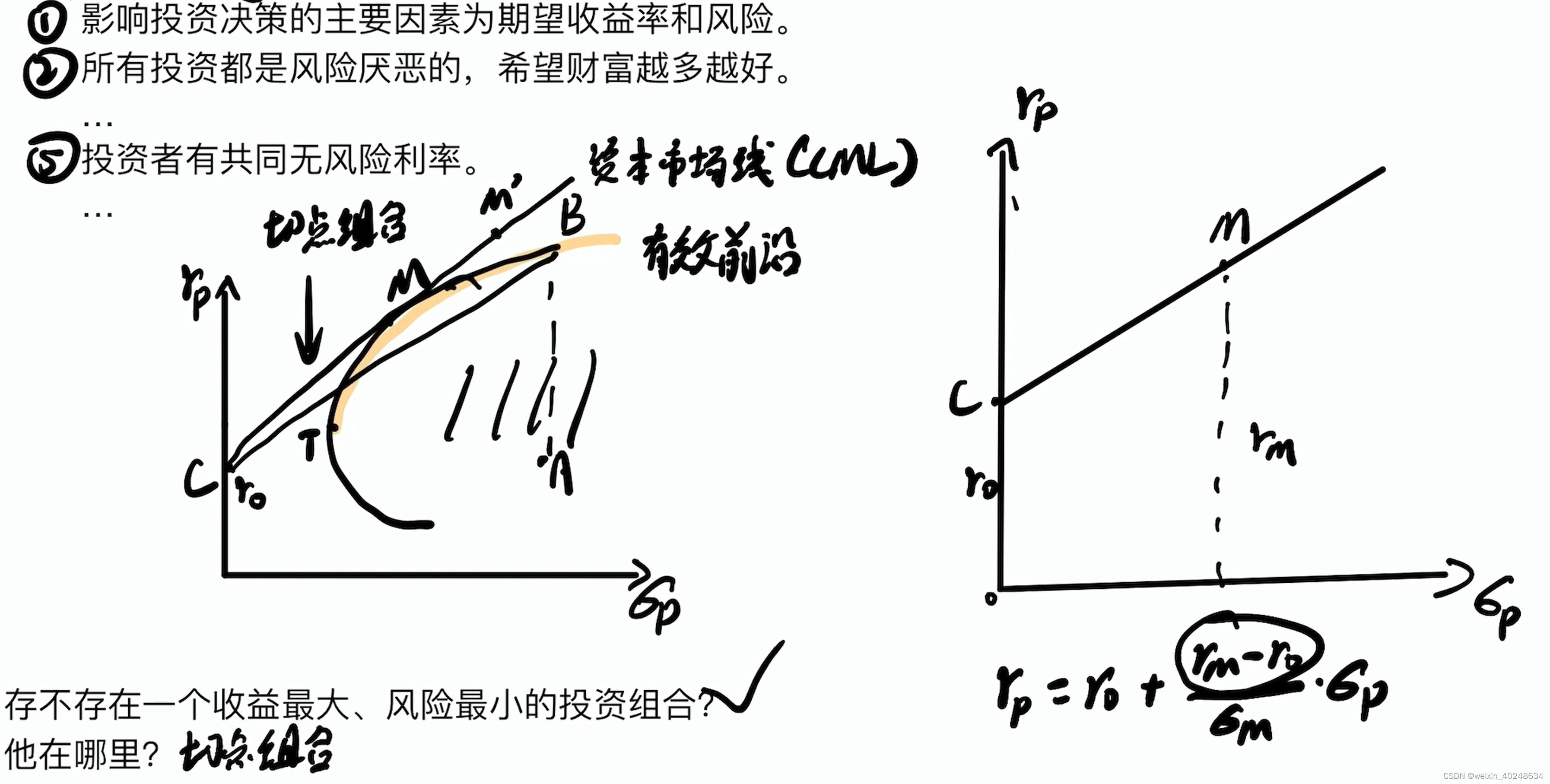
这条C-M直线描绘的对于整个市场的收益，其对于单支股票并不适应，所以后面换了个横轴, 为单个证券对整个市场的联动性
σ
i
,
M
σ
M
\frac{\sigma_{i,M}}{\sigma_M}
σMσi,M。
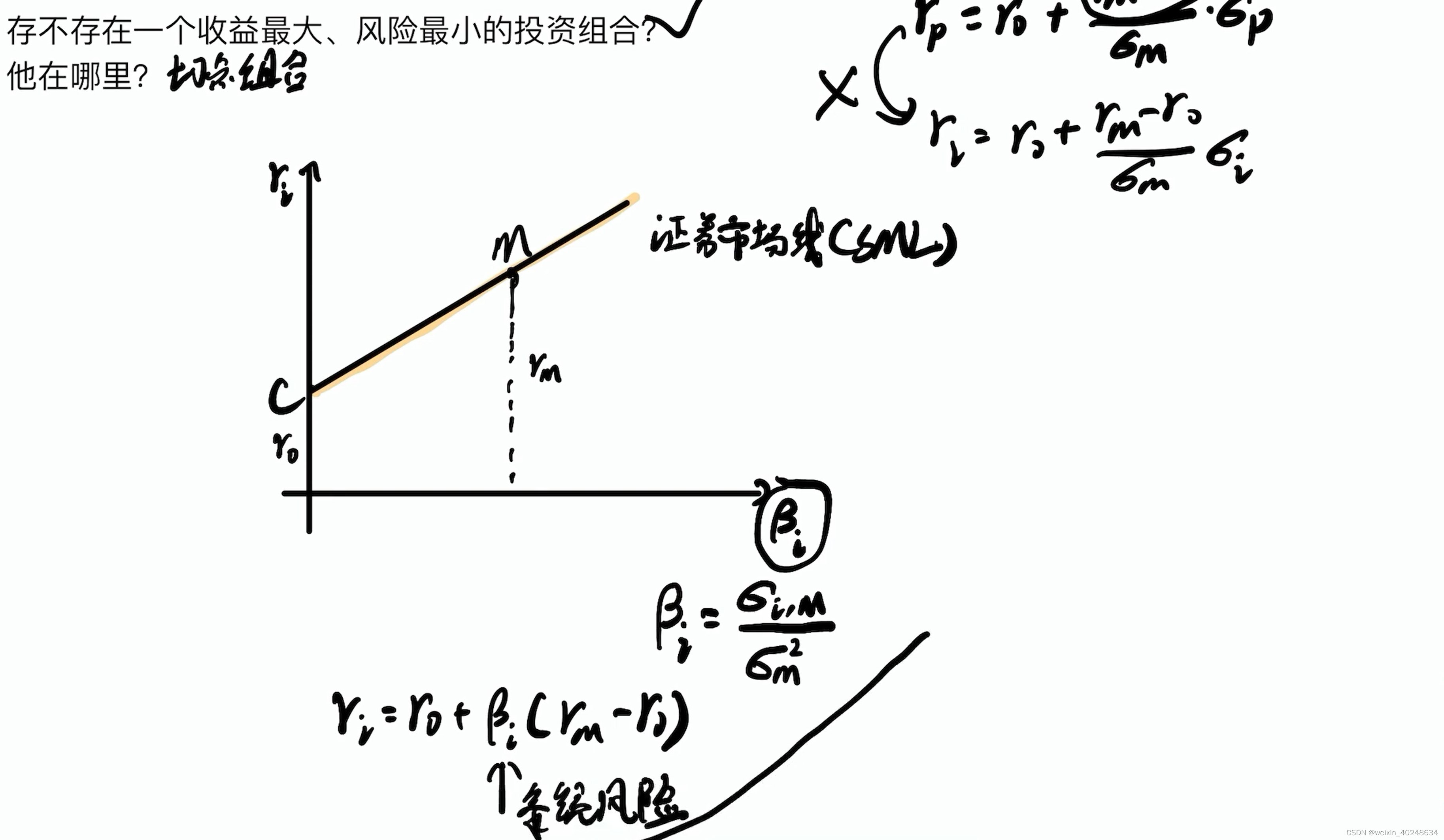
也就是CAPM公式了
E
[
R
i
]
=
R
f
+
c
o
v
(
R
i
,
R
M
)
v
a
r
(
R
M
)
(
E
[
R
M
]
−
R
0
)
c
o
v
(
R
M
,
R
M
)
v
a
r
(
R
M
)
=
R
f
+
c
o
v
(
R
i
,
R
M
)
v
a
r
(
R
M
)
(
E
[
R
M
]
−
R
0
)
E[R_i] = R_f +\frac{cov(R_i,R_M)}{var(R_M)} \frac{(E[R_M]-R_0)}{\frac{cov(R_M,R_M)}{var(R_M)}} = R_f +\frac{cov(R_i,R_M)}{var(R_M)}(E[R_M]-R_0)
E[Ri]=Rf+var(RM)cov(Ri,RM)var(RM)cov(RM,RM)(E[RM]−R0)=Rf+var(RM)cov(Ri,RM)(E[RM]−R0)
注意这
v
a
r
(
R
)
=
σ
2
(
R
)
var(R)=\sigma^2(R)
var(R)=σ2(R)
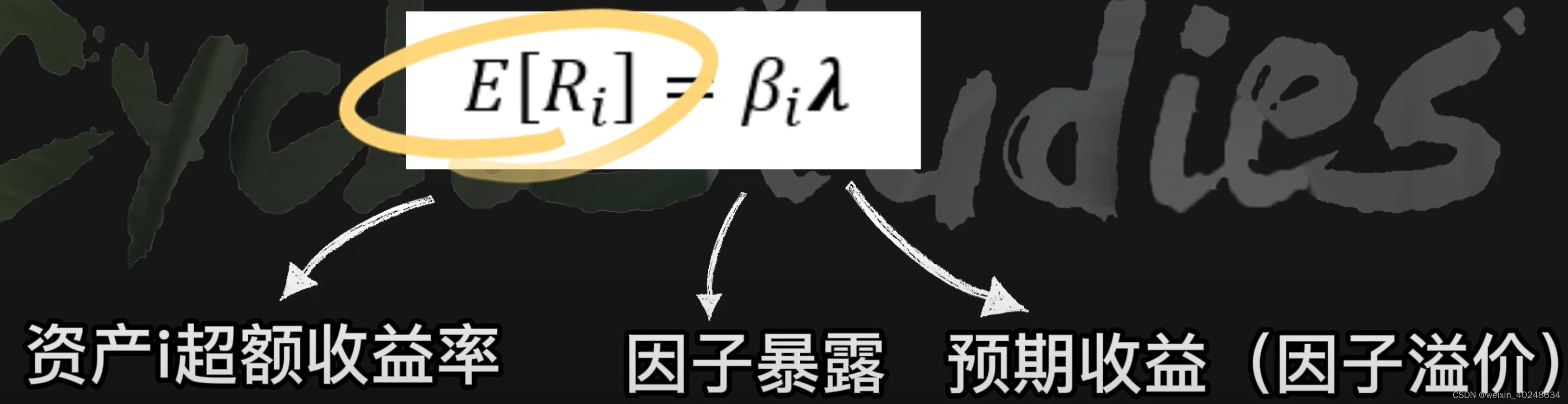
APT套利定价理论
截面数据 & 时间序列数据 & 面板数据
- 横截面数据，也称截面数据、静态数据，是统计学与计量经济学中的一类数据集，通过观察许多主体（如个人、公司、国家、地区等）在同一时间点或同一时间段截面上反映一个总体的一批（或全部）个体的同一特征变量的观测值。例如，经济普查数据、人口普查数据、家庭收入调查数据。横断面数据分析通常比较被选择的主体的差异。 -时间序列数据，小规模数据或者聚集数据在一系列时间点上被观测。
- 面板数据（或称纵向数据）是截面数据与时间序列数据的结合。面板数据不同于混合横截面数据（pooled cross-sectional data）。面板数据是对 同一主体的不同时间点的观测值。混合横截面数据是在不同时点从同一个大总体内部分别抽样，将所得到的数据混合起来的一种数据集。如许多关于个人、家庭和企业的调查，每隔一段时间，常常是每隔一年，重复进行一次，如果每个时期都抽取一个随机样本，那么把所得到的随机样本合并起来就给出一个混合横截面。
横截面数据可施加横截面回归，及对截面数据的回归分析。
定价误差
α
\alpha
α
alpha 出现的原因
如果alpha 显著不为0， 那么称之为异象（Anomaly）， 从投资的角度来说，我们就需要买入alpha显著不为0， alpha越大的资产
线性多因子模型
这里从单个时间点做分析，T时刻资产i的超额收益率
R
i
T
R_{iT}
RiT ；
α
i
\alpha_i
αi 表示第
i
i
i 个资产的定价误差，
β
i
\beta_i
βi表示因子暴露矩阵，
λ
T
\lambda_T
λT表示T时刻的因子收益率，
ϵ
i
T
\epsilon_{iT}
ϵiT 表示T时刻的随机扰动，
Fama-French三因子模型
三因子的计算公式
利用alpha大小进行购买股票
我们最后的目的就是为了得到alpha，使用alpha来判断资产的潜力.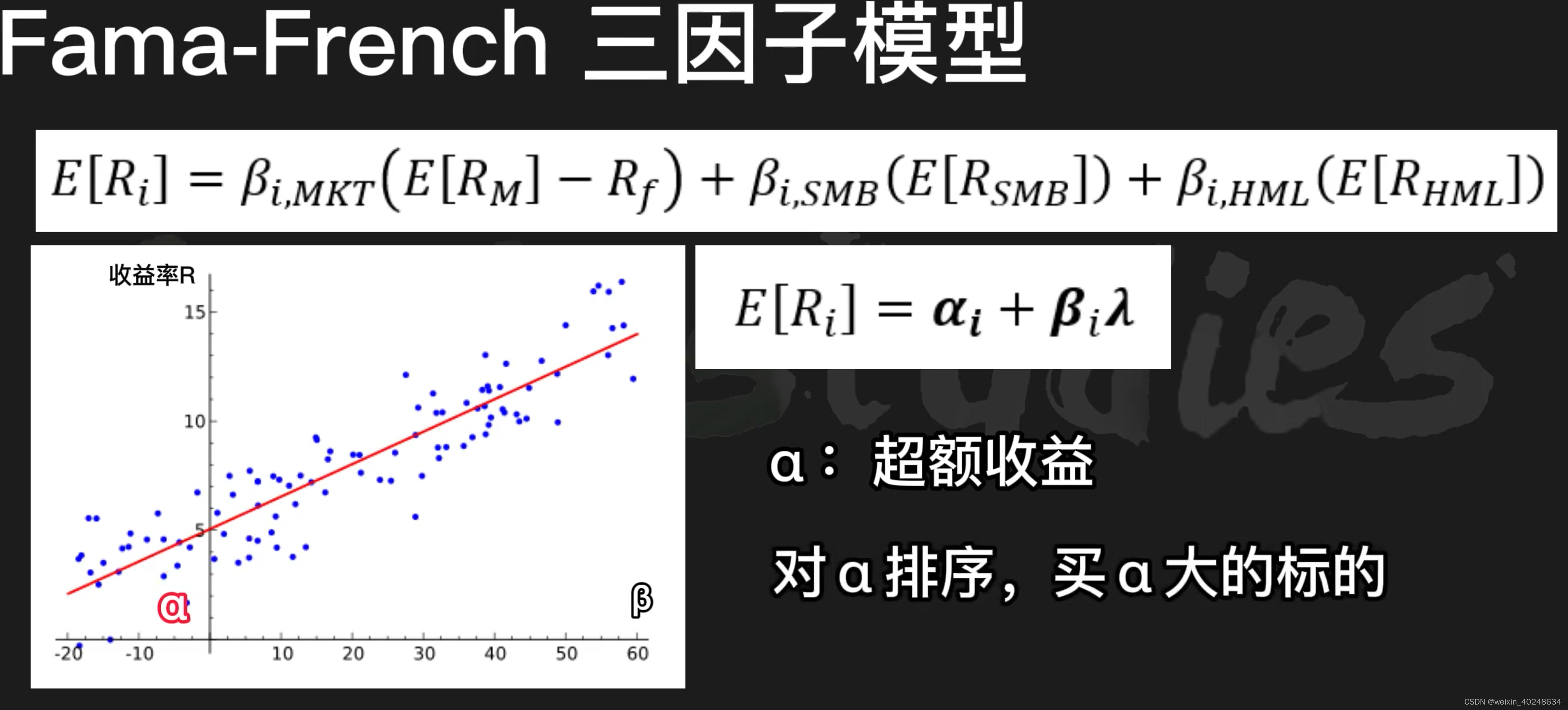
本文转载自: https://blog.csdn.net/weixin_40248634/article/details/129039498
版权归原作者 weixin_40248634 所有， 如有侵权，请联系我们删除。
版权归原作者 weixin_40248634 所有， 如有侵权，请联系我们删除。