文章目录
一、前言
距离阅读这篇论文也过去几天了,有些当初的想法也有所丢失。还是得记录一下理解过程,避免这么快速的忘记。精读这篇文章的原因还是来自于一些工作中的启发,人脸修复算法(face restoration)效果较好的基于可以分为3个流派,一种基于stylegan先验的GFPGAN、GPEN等,另外两种分别是基于transform和diffusion。而基于stylegan的方式通常都是采用 stylegan2。所以有必要熟悉一下stylegan2。stylegan2 只阅读论文或只阅读代码感觉整体的理解都会比较苦涩,结合两者感觉才可以理解的比较好一些。
二、简要介绍
stylegan2 相较于 stylegan 主要改进了几个地方,根据文中作者的用语,一个很常见的词就是
revisited
,重新审视了一代的一些结构、损失函数、正则化、训练方式等方面,并提出改进。根据文中的章节和描述,主要分为四大块,
(1)、水滴状伪影的修正(归一化的修改),作者详细的说明一代中使用AdaIN 的缺点,然后分析更好的结构,并直接把归一化操作融合进卷积权重内,变成卷积权重归一化,十分巧妙。
(2)、图像质量的的提升,其实是主要提出PPL(perceptual path length)这个东西,并利用这个东西做正则化。
(3)、关于渐进提升分辨率的做法,分析不同分辨率下用什么结构融合会比较好(skip or residual),不同分辨率的特征有没有充分使用上?
(4)、关于将图像投影到隐码 (latent space),怎么投影?利用这个特征,图像->latent->图像 来鉴别是自然图像还是模型生成的图像
三、详细解析
1、归一化的修改
水滴状问题如下图所示:
作者将stylegan的水滴状伪影定位到其中的AdaIN归一化模块,为什么这么说?作者认为分别归一化每个特征图的均值和方差,这样子每个特征和相邻特征之间的相对大小关系就被破坏了。AdaIN可以通过让生成器制造尖峰spike来主导整体分布,从而让其他位置的信号变小,逃过鉴别器的鉴别。尖峰就形成了水滴状,一种相较于其他位置很高的信号强度。
1.1生成器结构的修改
作者重新审视了一下生成器的结构,做出如下图的分离与简化。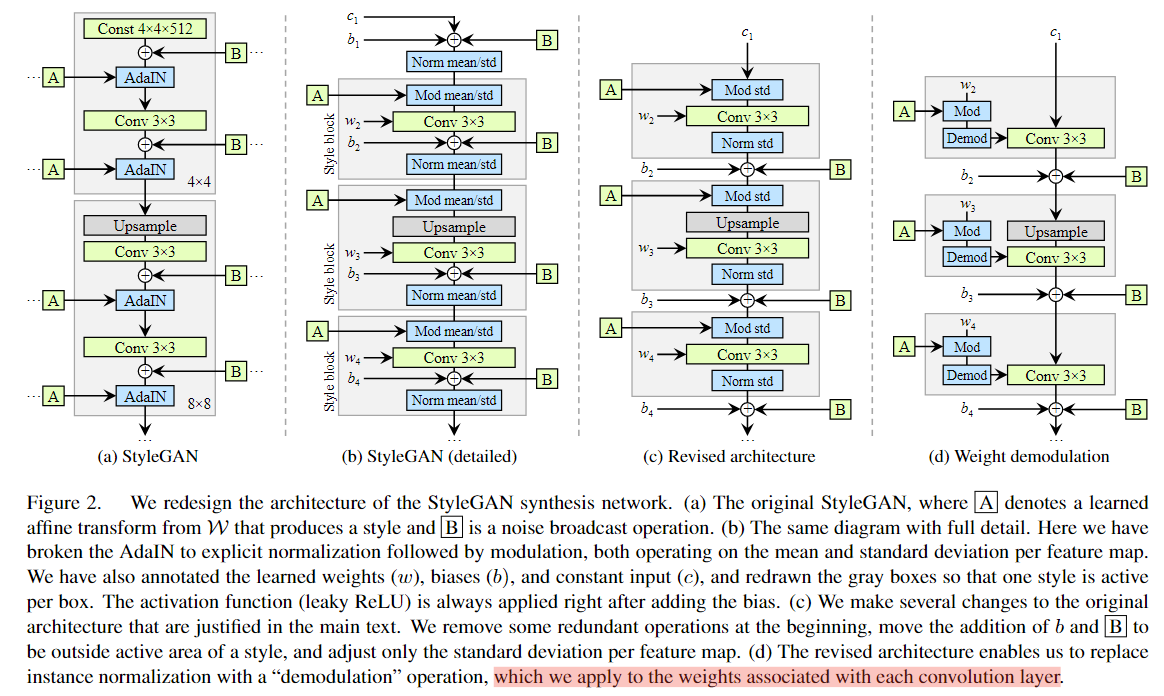
图a 为原始的StyleGAN结构,图b是分离出归一化层和style block的结构,至于为啥一个AdaIN可以分解成两个mean/std层,这需要涉及到图像风格转移方面的知识。AdaIN 可以看作是两个分布的叠加,
Adaptive Instance Normalization (AdaIN) 的公式如下:
AdaIN
(
x
,
y
)
=
σ
(
y
)
(
x
−
μ
(
x
)
σ
(
x
)
)
+
μ
(
y
)
\text{AdaIN}(x, y) = \sigma(y) \left( \frac{x - \mu(x)}{\sigma(x)} \right) + \mu(y)
AdaIN(x,y)=σ(y)(σ(x)x−μ(x))+μ(y)
其中:
- ( x ) 是内容图像的特征映射。
- ( y ) 是风格图像的特征映射。
- ( \mu(x) ) 和 ( \sigma(x) ) 分别是内容图像特征映射的均值和标准差。
- ( \mu(y) ) 和 ( \sigma(y) ) 分别是风格图像特征映射的均值和标准差。
在图b中,下面的Mod就是style嵌入过程,上面的归一化Norm就是内容的归一化x。原始 StyleGAN 在Style Block中应用偏差和噪声,导致它们的相对影响与当前在Style的大小成反比。这个可以理解Style和(偏置和噪声)同样作用于整个block,这个作用大另外一个就作用小了。作者觉得这样不太好,通过将偏置和噪声挪到Block之外,也就是针对归一化后的数据再增加偏置和噪声,可以获得更容易观测的结果。然后发现通过这个变化之后,发现仅仅对标准差Std进行归一化(Norm)和调制(Mod)就够了,不需要均值了,这个变化可以通过图c看到。这是一切重新设计的起点。
1.2重新审视实例归一化(Instance normalization)
StyleGAN 的主要优点之一是能够通过风格混合来控制生成的图像,即在推理时将不同的latent w 馈送到不同的层。这种方式可能会放大某些特征图的特征,因此这就是后面归一化操作Norm的存在意义,抵消这种放大,这样后续层可以继续控制图像的生成方向。因此去掉归一化操作的话虽然可以解决水滴伪影问题,却会失去一些尺度的控制。
因此,作者提出一种替代的归一化方案,这种方案可以两者兼顾(既要还要),同时解决水滴伪影问题并能够保持整体特征可控制。主要的思想是对要传入的特征图的数据进行归一化,但并不是强制的归一化!
我们看下图2c,每一个Style Block包含3个东西,调制(Mod)、卷积、归一化(Norm),调制的话就是将一些特征图的作用放大,作者想到,哎这是可以通过直接修改卷积权重做到吗?weight x scale = feature map x scale,于是,前面两个操作可以用一个卷积替换!

到这里或许会想,那后面那个归一化(Norm) 能不能也简化掉?
当然可以!后面的归一化操作就是为了抵消放大倍数s的影响,那只要计算他把方差放大了s,我们再用乘以 (1/s) 不就可以了?
以输入单位标准差为例,经过Mod,标准差变成(式子2),这是一个L2范数的结果,因此,解调(demod)也就是后续的Norm操作需要将标准差重新变成单位标准差,也就是需要除以sigma,那么这个操作又可以直接用卷积权重来实现(式子3)。因此整体调整后的结构就是图2d。这个调制方式并不是直接使用特征图,而是基于统计数据。
(ps:为了使实现更高效,作者使用了分组卷积,为了让式子3成立,作用为激活函数进行了缩放,这些都在代码中体现)


2、图像质量和生成器平滑(PPL相关内容)
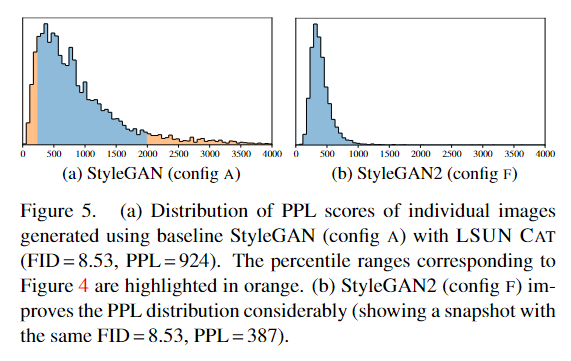
文章指出虽然FID和P&R指标在一定程度上可以作为生成器的指标,但是有些场景却不能够覆盖,并举了图13的例子,相同参数但是质量却差别很大。作者观察到感知图像质量和感知路径长度 (PPL) 之间的相关性,通过测量在隐码空间(latent space)发生小扰动情况下,生成图像之间的平均 LPIPS 距离,来量化从隐码空间到输出图像的映射平滑度。也就是给latent space添加点噪声,看生成图像之间的差距。小的PPL距离代表着较高的图像质量。作者通过图4举了个例子,通过在latent space采样,低PPL的图像质量高于高PPL的。

作者猜想PPL和图像质量的关系,认为在训练的时候由于鉴别器的惩罚作用,生成器最好的选择就是将高质量图像的latent space 拉大(让空间更平滑),让质量较差图像的latent space变得又急又小,这样鉴别器的损失就可以达到很小。但是作者提出,虽然低PPL代表图像,但并不是要等于0,因为等于0,生成图像就很单一,召回率就等于0了,训练图像不能被完全复现。因此,作者提出了一种基于PPL的正则化器,来制造更加平滑的生成器映射。由于正则化计算是很耗费资源的,因此作者首先提出一种适用于正则化的新优化点。也就是Lazy regularization 懒惰正则化。
什么是Lazy regularization,顾名思义就是让正则化不那么频繁的更新,这样会减少整体训练的时间,对资源的损耗会降低,论文中提到生成器的主要损失函数是logistics loss 和 正则化项(regularization terms),但作者通过实验证明,其实正则化项并不需要每次都更新,他每隔16次迭代更新一次就行,并不会影响生成器的结果。详情见表1 c行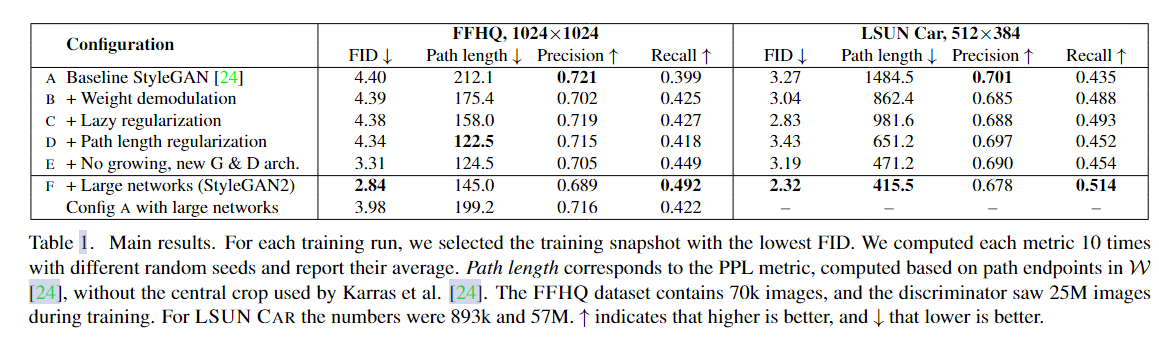
新的正则化优化技术同样可以用于作者新提出的基于路径长度正则化(path length regularization)。啥是路径长度正则化? 也就是通过在图像空间引入随机方向(随机噪声),计算latent w的梯度,理想情况下,无论方向怎么变化,w的梯度都要接近相等的长度,这就表明latent spcae和image space映射良好,也就是说,如果w中发生了固定大小a的变化,那么图像也会发生中固定大小b的变化。
正则化器可以设置为下式。
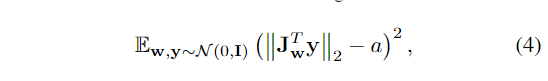
其中Jw是Jacobian matrix,也即生成器G(w) 和w的偏导数 (也就是图像y和w的偏导数),从式子中看,当偏导数和图像y正交,这个距离是最小的,损失也是最小的。由于考虑到Jacobian matrix矩阵的计算成本,作者直接用梯度*y代替,a也随着时间变化,是一个移动均值的结果,如下图所述。

从图5中可以看到,采用这种正则化技术可以让PPL变得更加紧凑(右侧),整体分布都比较小(代表高质量),但又不是0(召回率为0).
3、关于渐进式增长Progressive growing
作者指出渐进式增长在生成高分辨率图像方面很成功,但同时也存在问题,有很强的位置偏好。例如图6所示,在转头过程中原来应该一起移动的牙齿却固定不变。
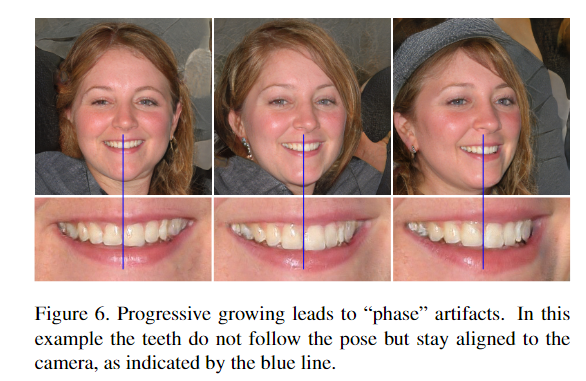
作者认为问题在于在渐进式增长中,每个分辨率暂时用作输出分辨率,迫使它生成最高频细节,这导致经过训练的网络在中间层具有过高的频率,从而出现移位不变性。作者想要在去掉缺点的前提下,保留渐进式增长的好处。主要做了两个事情。(1)采用其他结构,skip or residual network。(2) 观察不同分辨率对图像的贡献。
3.1采用替换结构(Alternative network)
通过简化MSG-GAN的不同分辨率的连接方式,来找到更好的结构,并通过实验结果确定了生成器应该用跳跃(skip)结构,鉴别器应该用残差结构(residual net)。具体结构和结果见下图。
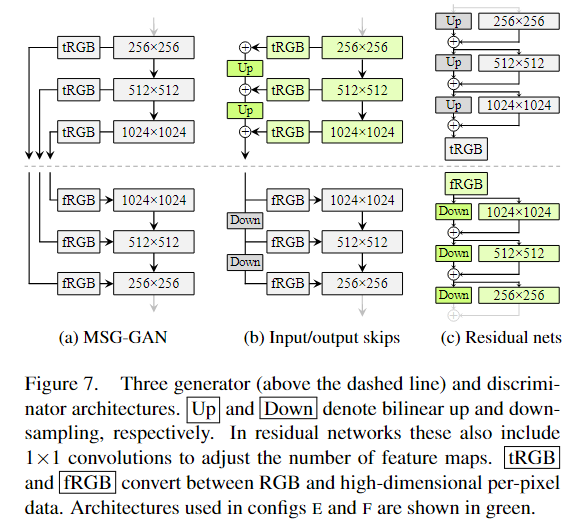
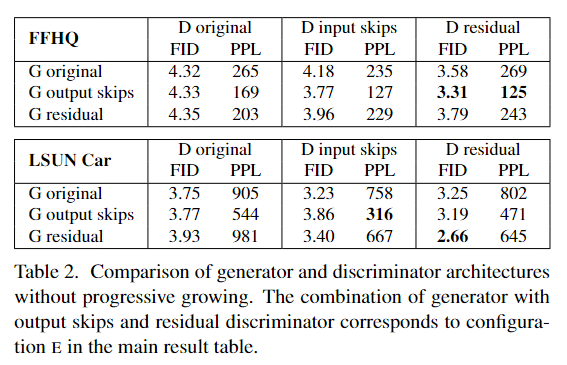
3.2不同分辨率的使用
采用上图7这种结构,并不是强制性的将低分辨率的图像特征转移到高分辨率图像,而是由网络自己优化确定方向,因此作者想要通过数据量化的方式来找到生成器在训练过程中依赖于特定分辨率的程度。具体怎么做呢?作者考虑到由于跳过生成器(图7b)通过显式地对来自多个分辨率的RGB值求和来生成图像,就可以通过测量它们对最终图像的贡献程度来估计相应层的相对重要性。在图 8a 中,作者将每个 tRGB 层产生的像素值的标准差绘制为训练时间的函数。总的计算 w 的 1024 个随机样本的标准偏差,然后并对值进行归一化,使它们总和为 100%。如图8a所示。
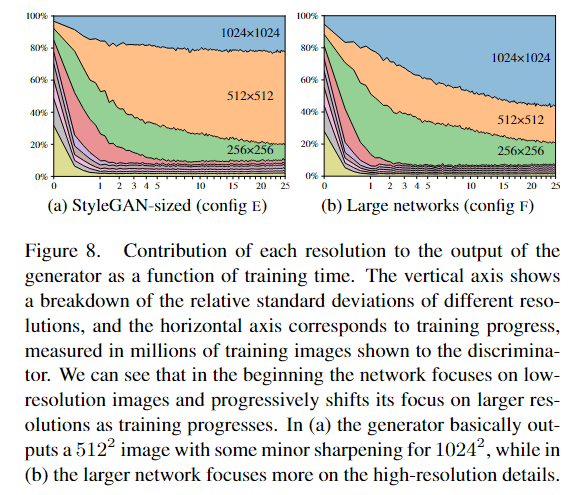
然后作者就发现,哎不对劲,怎么训练到最后,1024这个尺度的贡献还没512尺度的大?然后看了一下实际生成图像,发现1024的图像确实并没有这个尺度应该有的细节,反而像是512这种尺度加上一点锐化的图像。
作者考虑到,会不会是网络不够大的原因,限制了1024的尺度贡献呢?因此作者将最大尺度的特征图数量扩大两倍,重新训练,发现确实结果正常了许多,如图8b所示,1024的贡献变大了,然后计算了一下指标,确实提升了,如上面表1F配置所示。
4、图像投影到隐码空间(latent space)
4.1怎么投影?
反转生成网络 g 是一个具有许多应用的有趣问题,即通过隐空间中操纵图像,但这首先需要找到图像中原本的隐码 w。这个具体是怎么做的呢?给定一个图像,我们的目的是找到这个图像对应的隐码W以及噪声N。作者是怎么做的呢?
首先给定随机10000组的latent code z , 并通过映射网络(mapping network)映射到w空间,然后计算这10000组w的平均值
μ
(
w
)
\mu(w)
μ(w),并通过标准差来计算每一组w到中心
μ
\mu
μ的距离。同下面的表述一样。

初始化设置w=
μ
(
w
)
\mu(w)
μ(w) ,噪声n 是单位噪声N(0,I),w和n为训练优化的参数,学习率设置:前50次用斜坡函数从0到最大值
λ
max
=
0.1
\lambda_{\text{max}}=0.1
λmax=0.1,然后最后250迭代,用余弦时间表(cosine schedule)下降到0。前面750次迭代在计算损失函数的时候对w添加高斯噪声,强度从1到0,作者说这增加了优化的随机性并稳定全局最优。
作者提到,由于现在是在优化噪声图和w,需要将信号完全摒除掉,因此在损失函数,除了对图像质量进行监督,还需要对噪声进行正则化。以下是图像质量loss,就是原始图像和在给定w、n下生成图像的LPIPS距离
L
image
=
D
LPIPS
[
x
,
g
(
w
~
,
n
0
,
n
1
,
…
)
]
L_{\text {image }}=D_{\text {LPIPS }}\left[x, g\left(\tilde{\mathbf{w}}, \boldsymbol{n}_0, \boldsymbol{n}_1, \ldots\right)\right]
Limage =DLPIPS [x,g(w~,n0,n1,…)],下图是噪声正则化的具体操作,多个尺度下偏移x,y一个像素,计算点积,如果噪声是高斯分布(不带任何信号),那么,这个损失函数就为0。注:作者说下采样每个步骤都乘以2来保持单位方差,但是在代码中好像没看到。

图18就是存在噪声正则化的效果,噪声图不带有信号分量。
4.2生成图像的属性
对应文中5.1章节,这个章节的目的就是提出另外一种鉴别生成图像和自然图像的方式,那就是将图像投影到隐码空间w,如果能够投影回去,那么他就是假图像(生成图像)。那么怎么看投影是不是准确呢?就是计算原来图像和重新合成图像是LPIPS距离。
D
LPIPS
[
x
,
g
(
g
~
−
1
(
x
)
)
]
D_{\text {LPIPS }}\left[x, g\left(\tilde{g}^{-1}(x)\right)\right]
DLPIPS [x,g(g~−1(x))] 。从图10可以看到,使用StyleGAN2生成的图像可以投影到W中,并反生成十分接近的图像,就可以确定这是生成的假图像,真实图像是没有办法投影到非常接近的地步的,重新生成的图像和原图也有较大的差异。stylegan 第一代使用这种方法没办法做到,区分不开。这种方式作者说是
attribute a generated image to its source
归源法?
未来展望
作者的未来展望:
1、研究路径长度正则化的进一步改进,例如,通过用数据驱动的特征空间指标来替换像素空间 L2 距离。
2、考虑到 GAN 的实际部署,作者认为找到减少训练数据需求的新方法将很重要。因为获取大量数据在很多应用是比较难的。
具体代码理解放到下一篇了。。
版权归原作者 RichardCV 所有, 如有侵权,请联系我们删除。