许多机器学习方法中, 尤其是深度学习中的神经网络, 都存在几个问题:
- 模型容易过拟合.
- 模型在受到微小扰动(噪声)后, 预测结果会受相当程度的影响.
为了减少过拟合现象, 典型的监督学习中会添加一个新的损失项. 在半监督学习中, 同样存在一种正则化方法, 即一致性正则化(Consistency Regularization).
一致性正则化
具体来说, 基于平滑假设和聚类假设, 具有不同标签的数据点在低密度区域分离, 并且相似的数据点具有相似的输出. 那么, 如果对一个未标记的数据应用实际的扰动, 其预测结果不应该发生显著变化, 也就是输出具有一致性.
由于这种方法一般基于模型输出的预测向量, 不需要具体的标签, 所以其刚好能能应用于半监督学习. 通过在未标记数据上构造添加扰动后的预测结果
y
~
\tilde{y}
y~ 与正常预测结果
y
y
y 之间的无监督正则化损失项, 提高模型的泛化能力.
数学化表达如下:
D
[
p
m
o
d
e
l
(
y
∣
A
u
g
m
e
n
t
(
x
)
,
θ
)
,
p
m
o
d
e
l
(
y
∣
A
u
g
m
e
n
t
(
x
)
,
θ
)
]
D[p_{model}(y\vert \mathrm{Augment}(x),\theta),p_{model}(y\vert \mathrm{Augment}(x),\theta)]
D[pmodel(y∣Augment(x),θ),pmodel(y∣Augment(x),θ)]
其中,
D
D
D 为度量函数, 一般采用 KL 散度或 JS 散度, 当然也可使用交叉熵或平方误差等.
A
u
g
m
e
n
t
(
⋅
)
\mathrm{Augment(\cdot)}
Augment(⋅) 是数据增强函数, 会添加一些噪声扰动,
θ
\theta
θ 为模型参数, 多个模型的参数可以共用, 或者通过一些转换建立联系(Mean-Teacher), 如 EMA , 也可以相互独立(Daul-Student).
A
u
g
m
e
n
t
(
⋅
)
\mathrm{Augment}(\cdot)
Augment(⋅) 的类型在近几年的论文有以下几种:
- 常规的数据增强, 平移旋转, 或随机 dropout 等, 如 Π \Pi Π-model.
- 时序移动平均, 如 Temporal Ensembling, Mean-Teacher, SWA.
- 对抗样本扰动, 如 VAT, Adversarial Dropout.
- 高级数据增强, 如 UDA, Self-supervised SSL.
- 线性混合, 如 MixMatch.
blog 文章传送门:
Π \Pi Π-Model 和 Temporal Ensembling- Mean-Teacher
- Dual-Students
- Adversarial Dropout
- VAT
- ICT
- UDA
1. Ladder Networks
Ladder Networks 文献暂时没看, 内容以后更新.
2.
Π
\Pi
Π-Model
Π
\Pi
Π-Model 模型如下图所示:

每个 epoch 中, 一个样本
x
i
x_i
xi (同时包含有标记和无标记样本)前向传播两次, 通过 data augmentation 和 dropout 注入扰动, 由于前向传播两次, 所以得到两个预测向量
z
i
z_i
zi 和
z
~
i
\tilde{z}_i
z~i, 然后计算均方误差. 基于一致性正则化, 模型希望在注入扰动后得到的结果应该与原来一致, 所以,
Π
\Pi
Π-model 希望
z
i
z_i
zi 和
z
~
i
\tilde{z}_i
z~i 尽可能一致.
单独对于有标记样本来说, 其前向传播一次, 注入扰动后在预测值与真实值之间进行交叉熵计算. 最后将两个损失函数进行加权求和即为损失函数
l
o
s
s
loss
loss.
Π
\Pi
Π-Model 算法伪代码如下:

注意: 加权系数
w
(
t
)
w(t)
w(t) 随时间变化而变化, 在训练刚开始时, 我们希望有标记样本占据主要部分, 因此交叉熵损失比重应该大, 随着训练过程的进行, 希望在无标记数据上的损失的比重逐渐变大, 即 ramp-up 过程.
3. Temporal Ensembling
Temporal Ensembling 模型如下图所示:
与
Π
\Pi
Π-Model 相比, 训练过程的每一个 epoch 中, 一个样本只前向传播一次得到
z
z
z, 而另一个
z
~
\tilde{z}
z~ 则使用之前 epoch 得到的预测结果来充当, 具体做法为用指数平滑(EMA)来计算, 计算结果需要利用一个额外的空间来存储.
Temporal Ensembling 算法伪代码如下:
4. Mean-Teacher
针对 Temporal Ensembling 的一些缺点做出了改进. 此前的 Temporal Ensembling 在每个 epoch 只进行一次 EMA, 无法满足大型数据集的学习, 且无法实现模型的在线训练. 为了克服这个问题, Mean Teacher 能在每个 epoch 中的每个 step 进行模型权重的更新. 也就是将原来计算输出向量
z
~
\tilde{z}
z~ 的过程变成了计算整个网络的参数
θ
\theta
θ.
Mean Teacher 算法模型如下:
在 Mean Teacher 中, 使用两个模型: Student Model 和 Teacher Model, 两个模型架构相同. 其中, Teacher 的参数由 Student 计算指数移动平均值(EMA):
θ
t
′
=
α
θ
t
−
1
′
+
(
1
−
α
)
θ
t
\theta'_t=\alpha\theta'_{t-1}+(1-\alpha)\theta_t
θt′=αθt−1′+(1−α)θt
其中,
θ
t
\theta_t
θt,
θ
t
′
\theta'_t
θt′ 分别为 Student 和 Teacher 的参数. 当
α
=
0
\alpha=0
α=0 时, Mean Teacher 与
Π
\Pi
Π-model 在形式上等价.
5. Dual-Students
与 Mean-Teacher 相比, Dual Student 用另一个学生代替老师. 两名 Student 共享具有不同初始状态的相同网络架构并分别更新, 避免 Mean-Teacher 中的权重耦合问题带来的局限性, 因为 Teacher 本质上是 Student 的 EMA.
Dual Student 通过同时训练两个独立的模型来获得松耦合的目标. Dual Student 模型如下图所示:
然而, 这两个模型的输出可能相差很大, 直接应用一致性约束会导致它们通过交换错误的知识而相互崩溃. 于是提出了一种有效的方法来克服这个问题, 即只交换模型的可靠知识. 为此需要解决两个问题:
- 问题1. 如何定义和获取模型的可靠知识.
- 问题2. 如何相互交换知识.
为解决问题1, 引入稳定样本(Stable Sample)概念. 定义如下: 给定一个常数
ξ
∈
[
0
,
1
)
\xi \in [0, 1)
ξ∈[0,1), 一个满足平滑假设的数据集
D
⊆
R
m
\mathcal{D} \subseteq \mathbb{R}^m
D⊆Rm 和一个模型
f
:
D
→
[
0
,
1
]
n
f : \mathcal{D} \rightarrow [0, 1]^n
f:D→[0,1]n, 对所有
x
∈
D
x \in D
x∈D 满足
∥
f
(
x
)
∥
1
=
1
\lVert f(x)\rVert_1 = 1
∥f(x)∥1=1, 且:
∀ x ‾ ∈ D \forall \overline{x} \in \mathcal{D} ∀x∈D, 在 x x x 附近, 它们的预测标签是相同的.x x x 满足不等式: ∥ f ( x ) ∥ ∞ > ξ \lVert f(x)\rVert_\infty > \xi ∥f(x)∥∞>ξ
则
x
x
x 是关于
f
f
f 的稳定样本. 如下图中, 只有
x
3
x_3
x3,
x
‾
3
\overline{x}_3
x3 满足.

为解决问题2, 引入稳定约束概念. Student
i
i
i 在样本
x
x
x 上的稳定约束写为:
L
s
t
a
i
(
x
)
=
{
{
ε
x
i
>
ε
x
j
}
1
L
m
s
e
(
x
)
,
R
x
i
=
R
x
j
=
1
R
x
j
L
m
s
e
(
x
)
,
o
t
h
e
r
v
i
s
e
\mathcal{L}_{sta}^i(x) = \begin{cases} \{\varepsilon_x^i > \varepsilon_x^j\}_1 \mathcal{L}_{mse}(x),\mathcal{R}_x^i=\mathcal{R}_x^j=1 \\ \mathcal{R}_x^j \mathcal{L}_{mse}(x),othervise \\ \end{cases}
Lstai(x)={{εxi>εxj}1Lmse(x),Rxi=Rxj=1RxjLmse(x),othervise
具体内容可通过上面传送门中的文章进行阅读.
Student
i
i
i 的最终约束是三个部分的组合: 分类约束、每个模型中的一致性约束和模型之间的稳定性约束. 如下:
L
i
=
L
c
l
s
i
+
λ
1
L
c
o
n
i
+
λ
2
L
s
t
a
i
\mathcal{L}^i=\mathcal{L}_{cls}^i+\lambda_1\mathcal{L}_{con}^i+\lambda_2\mathcal{L}_{sta}^i
Li=Lclsi+λ1Lconi+λ2Lstai
Daul-Student 训练过程如下:
6. Fast-SWA
Fast-SWA 文献暂时没看, 内容以后更新.
7. Virtual Adversarial Training(VAT)
(PS: 这篇论文中还有些东西没有明白, 后面会继续深入理解)
VAT 是一种基于熵最小化的正则方法, 并提出一种对于给定输入评估模型输出条件分布局部光滑性的虚拟对抗损失, 虚拟对抗性损失可被定义为每个输入数据点周围的条件标签分布对局部扰动的鲁棒性. VAT 主要思想为: 为提升模型的鲁棒性, 对输入样本加入对抗性扰动, 将其与原始样本做一致性正则化.
在对抗训练中, 对抗方向定义为在输入数据点处, 可以最大程度地降低模型正确分类的概率, 或者是可以最大程度地"偏离"模型预测与正确标签的方向. 基于此, VAT 中引入虚拟对抗方向, 与传统对抗训练不同的是, 即使在没有标签信息的情况下, 也可以在未标记的数据点上定义虚拟对抗方向, 就好像有一个"虚拟"标签一样.
VAT 中的损失函数如下:
D
[
q
(
y
∣
x
∗
)
,
p
(
y
∣
x
∗
+
r
q
a
d
v
,
θ
)
]
D[q(y\vert x_*),p(y\vert x_*+r_{qadv},\theta)]
D[q(y∣x∗),p(y∣x∗+rqadv,θ)]
r
q
a
d
v
:
=
arg max
r
;
∣
∣
r
∣
∣
≤
ϵ
D
[
q
(
y
∣
x
∗
)
,
p
(
y
∣
x
∗
+
r
,
θ
)
]
r_{qadv} :=\underset{r;\vert\vert r\vert\vert \leq \epsilon}{\argmax} D[q(y\vert x_*),p(y\vert x_*+r,\theta)]
rqadv:=r;∣∣r∣∣≤ϵargmaxD[q(y∣x∗),p(y∣x∗+r,θ)]
实际上我们没有关于
q
(
y
,
x
u
l
)
q(y,x_{ul})
q(y,xul) 的直接信息, 因此采取策略用
p
(
y
∣
x
,
θ
)
p(y\vert x,\theta)
p(y∣x,θ) 替换
q
(
y
,
x
)
q(y,x)
q(y,x). 如果带标签的样本比较多时,
p
(
y
∣
x
,
θ
)
p(y\vert x,\theta)
p(y∣x,θ) 会逼近
q
(
y
∣
x
)
q(y\vert x)
q(y∣x), 即用
p
(
y
∣
x
,
θ
)
p(y\vert x,\theta)
p(y∣x,θ) 生成的虚拟标签代替不知道的标签, 并根据虚拟标签计算对抗方向, 因此
q
(
y
∣
x
)
q(y\vert x)
q(y∣x) 用上一步的
p
(
y
∣
x
,
θ
^
)
p(y\vert x,\hat{\theta})
p(y∣x,θ^) 替代, 损失函数更新如下:
L
D
S
(
X
∗
,
θ
)
:
=
D
[
p
(
y
∣
x
∗
,
θ
^
)
,
p
(
y
∣
x
∗
+
r
v
a
d
v
,
θ
)
]
{\rm LDS}(X_*,\theta):=D[p(y\vert x_*,\hat{\theta}),p(y\vert x_*+r_{vadv},\theta)]
LDS(X∗,θ):=D[p(y∣x∗,θ^),p(y∣x∗+rvadv,θ)]
r
v
a
d
v
:
=
arg max
r
;
∣
∣
r
∣
∣
≤
ϵ
D
[
p
(
y
∣
x
∗
,
θ
^
)
,
p
(
y
∣
x
∗
+
r
)
]
r_{vadv} :=\underset{r;\vert\vert r\vert\vert \leq \epsilon}{\argmax} D[p(y\vert x_*,\hat{\theta}),p(y\vert x_*+r)]
rvadv:=r;∣∣r∣∣≤ϵargmaxD[p(y∣x∗,θ^),p(y∣x∗+r)]
综上, 给整个目标函数加上损失函数, 这里损失函数取平均, 最终得到完整的目标函数, 如下所示:
R
v
a
d
v
(
D
l
,
D
u
l
,
θ
)
:
=
1
N
l
+
N
u
l
∑
x
∗
∈
D
l
,
D
u
l
L
D
S
(
x
∗
,
θ
)
\mathcal{R}_{vadv}(\mathcal{D}_l,\mathcal{D}_{ul},\theta):=\frac{1}{N_l+N_{ul}}\sum_{x_*\in \mathcal{D}_l,\mathcal{D}_{ul}} {\rm LDS}(x_*,\theta)
Rvadv(Dl,Dul,θ):=Nl+Nul1x∗∈Dl,Dul∑LDS(x∗,θ)
l
o
s
s
=
L
(
D
l
,
θ
)
+
α
R
v
a
d
v
(
D
l
,
D
u
l
,
θ
)
loss = \mathcal{L}(\mathcal{D}_l,\theta)+\alpha \mathcal{R}_{vadv}(\mathcal{D}_l,\mathcal{D}_{ul},\theta)
loss=L(Dl,θ)+αRvadv(Dl,Dul,θ)
其中
L
(
D
l
,
θ
)
\mathcal{L}(\mathcal{D}_l,\theta)
L(Dl,θ) 为带标签数据的负对数似然函数. 整个正则化过程中, 只有两个超参数: 正则化系数:
α
\alpha
α, 对抗方向的范数约束:
ϵ
\epsilon
ϵ.
下图显示了 VAT 如何在二维合成数据集上进行半监督学习: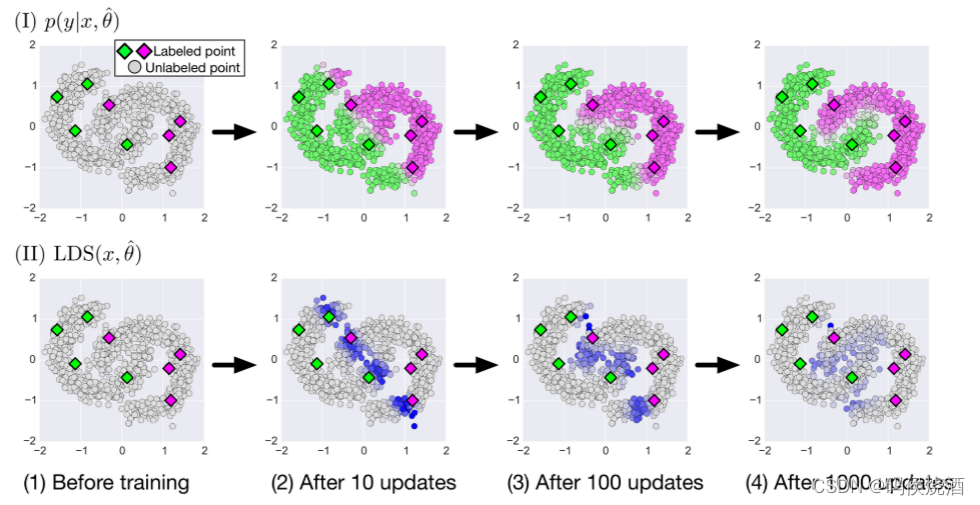
在二维空间中生成了 8 个标记数据点(
y
=
1
y = 1
y=1 和
y
=
0
y =0
y=0 分别为绿色和紫色), 以及1000个未标记数据点. 第一行 (I) 中的面板表示在算法不同阶段的未标记输入点上的预测
p
(
y
=
1
∣
x
,
θ
)
p(y=1\vert x,\theta)
p(y=1∣x,θ). 使用连续颜色来指定
p
(
y
=
1
∣
x
,
θ
)
p(y=1\vert x,\theta)
p(y=1∣x,θ) 的预测值, 其中绿色、灰色和紫色分别对应值 1.0、0.5 和 0.0. 第二行 (II) 中的面板是正则化项
L
D
S
(
x
,
θ
^
)
LDS(x,\hat{\theta})
LDS(x,θ^) 在输入点上的热图. 与灰色点相比, 蓝色点上的
L
D
S
LDS
LDS 值相对较高, 我们使用 KL 散度来选择式(5)中的
D
D
D.
8. Adversarial Dropout(AdD)
是 VAT 的变种, VAT 是在 input data 上加对抗扰动, AdD 则是在网络中间层进行对抗性 dropout.
结合对抗 dropout 的附加损失函数的描述如下:
L
A
d
D
(
x
,
y
,
ϵ
s
;
θ
,
δ
)
:
=
D
[
g
(
x
,
y
,
θ
)
,
f
θ
(
x
,
ϵ
a
d
v
)
]
\mathcal{L}_{AdD}(x,y,\epsilon^s;\theta,\delta):=D[g(x,y,\theta),f_\theta(x, \epsilon^{adv})]
LAdD(x,y,ϵs;θ,δ):=D[g(x,y,θ),fθ(x,ϵadv)]
其中
ϵ
a
d
v
:
=
arg max
ϵ
∥
ϵ
s
−
ϵ
∥
≤
δ
H
D
[
g
(
x
,
y
,
θ
)
,
f
θ
(
x
,
ϵ
)
]
\epsilon^{adv}:=\argmax_\epsilon \lVert \epsilon^s-\epsilon \rVert \leq \delta H^{D[g(x,y,\theta),f_\theta(x, \epsilon)]}
ϵadv:=ϵargmax∥ϵs−ϵ∥≤δHD[g(x,y,θ),fθ(x,ϵ)],
ϵ
a
d
v
\epsilon^{adv}
ϵadv 为 adversarial dropout mask,
ϵ
s
\epsilon^s
ϵs 为随机采样 dropout mask,
H
H
H 为 dropout layer 的维度.
引入边界条件
∥
ϵ
s
−
ϵ
∥
2
≤
δ
H
\lVert \epsilon^s-\epsilon\rVert_2 \leq \delta H
∥ϵs−ϵ∥2≤δH. 如果没有这个约束, 具有对抗 dropout 的网络可能会变成没有连接的神经网络层.
在对抗性训练的一般形式中, 关键点是线性扰动
γ
a
d
v
\gamma^{adv}
γadv 的存在. 可以将具有对抗性扰动的输入解释为对抗性噪声输入
x
~
a
d
v
=
x
+
γ
a
d
v
\tilde{x}^{adv} = x + \gamma^{adv}
x~adv=x+γadv. 从这个角度来看, 对抗训练的作者将对抗方向限制在加性高斯噪声
x
~
=
x
+
γ
0
\tilde{x} = x + \gamma^0
x~=x+γ0 的空间上, 其中
γ
0
\gamma^0
γ0 是输入层上的采样高斯噪声. 相比之下, 对抗性 dropout 可以被认为是通过 masking 隐藏单元产生的噪声空间,
h
~
(
a
d
v
)
=
h
⊙
ϵ
a
d
v
\tilde{h}^{(adv)}=h\odot \epsilon^{adv}
h~(adv)=h⊙ϵadv,
ϵ
a
d
v
\epsilon^{adv}
ϵadv 是对抗性选择的 dropout 状态. 如果假设对抗性训练是输入上的高斯加性扰动, 则扰动本质上是线性的, 但如果对抗性 dropout 施加在多个层上, 则对抗性 dropout 可能是非线性扰动.
学习的完整目标函数由下式给出:
l
(
y
,
f
θ
(
x
,
ϵ
s
)
)
+
λ
L
A
d
D
(
x
,
y
,
ϵ
s
;
θ
,
δ
)
l(y,f_\theta(x,\epsilon^s))+\lambda\mathcal{L}_{AdD}(x,y,\epsilon^s;\theta,\delta)
l(y,fθ(x,ϵs))+λLAdD(x,y,ϵs;θ,δ)
其中
l
(
y
,
f
θ
(
x
,
ϵ
s
)
)
l(y,f_\theta(x,\epsilon^s))
l(y,fθ(x,ϵs)) 是
ϵ
s
\epsilon^s
ϵs 中
x
x
x 对应的
y
y
y 的负对数似然.
9. Interpolation Consistency Training(ICT)
有研究表明: 对抗性扰动训练会损害泛化性能. 为了克服这个问题, 便提出了插值一致性训练(ICT), 简单来说, ICT 通过在未标记点
u
1
u_1
u1 ,
u
2
u_2
u2 的插值
α
u
1
+
(
1
−
α
u
2
)
\alpha u_1 + (1-\alpha u_2)
αu1+(1−αu2) 上的一致性预测
f
(
α
u
1
+
(
1
−
α
u
2
)
)
=
α
f
(
u
1
)
+
(
1
−
α
)
f
(
u
2
)
f(\alpha u_1 + (1-\alpha u_2))=\alpha f(u_1)+(1-\alpha)f(u_2)
f(αu1+(1−αu2))=αf(u1)+(1−α)f(u2) 来规范半监督学习.
为什么这种插值的策略有效呢? 因为只有在决策边界的数据点才更加有效, 因为对于这些点加入扰动之后, 可能把这个点变为另外一类, 可以提高模型的决策难度, 提升泛化能力.
根据 mixup 式子:
M
i
x
λ
(
a
,
b
)
=
λ
a
+
(
1
−
λ
)
b
{\rm Mix}_{\lambda}(a,b)=\lambda a + (1-\lambda)b
Mixλ(a,b)=λa+(1−λ)b
ICT 训练分类器
f
θ
f_\theta
fθ 以在未标记点的插值中提供一致性预测:
f
θ
(
M
i
x
λ
(
u
j
,
u
k
)
)
≈
M
i
x
λ
(
f
θ
′
(
u
j
)
,
f
θ
′
(
u
k
)
)
f_\theta({\rm Mix}_{\lambda}(u_j,u_k))\approx {\rm Mix}_\lambda(f_{\theta'}(u_j),f_{\theta'}(u_k))
fθ(Mixλ(uj,uk))≈Mixλ(fθ′(uj),fθ′(uk))
其中
θ
′
\theta'
θ′ 时
θ
\theta
θ 的滑动平均.
在监督学习环境中, mixup 是实现大边距决策边界的一种方法. 在 mixup 中, 通过强制预测模型在样本之间线性变化, 将决策边界推离类别边界, 通过训练模型
f
θ
f_\theta
fθ 来预测
M
i
x
λ
(
u
j
,
u
k
)
{\rm Mix}_λ(u_j,u_k)
Mixλ(uj,uk) 的"假标签"
M
i
x
λ
(
f
θ
′
(
u
j
)
,
f
θ
′
(
u
k
)
)
{\rm Mix}_\lambda (f_{\theta'}(u_j),f_{\theta'}(u_k))
Mixλ(fθ′(uj),fθ′(uk)) 来将 mixup 扩展到半监督学习.
ICT 模型如下图所示:
对于有标记数据, 直接计算其预测结果
y
^
i
\hat{y}_i
y^i 与真实标签
y
i
y_i
yi 之间的交叉熵损失. 对两个未标记点
u
j
u_j
uj 和
u
k
u_k
uk, 计算它们的假标签
y
^
j
=
f
θ
′
(
u
j
)
\hat{y}_j=f_{\theta'}(u_j)
y^j=fθ′(uj) 和
y
^
k
=
f
θ
′
(
u
k
)
\hat{y}_k=f_{\theta'}(u_k)
y^k=fθ′(uk), 然后, 计算插值
u
m
=
M
i
x
λ
(
u
j
,
u
k
)
u_m={\rm Mix}_λ(u_j,u_k)
um=Mixλ(uj,uk), 以及该位置的模型预测
y
^
m
=
f
θ
′
(
u
m
)
\hat{y}_m=f_{\theta'}(u_m)
y^m=fθ′(um). 接着, 更新参数
θ
\theta
θ 以使预测
y
^
m
\hat{y}_m
y^m 更接近于假标签的插值
M
i
x
λ
(
y
^
j
,
y
^
k
)
{\rm Mix}_λ(\hat{y}_j,\hat{y}_k)
Mixλ(y^j,y^k).
10. Unsupervised Data Augmentation(UDA)
为了加强一致性, 现有方法通常采用简单的噪声注入方法, 例如添加高斯噪声. 相比之下, UDA 中使用监督学习的更强的数据增强作用于半监督的一致性训练框架中, 研究表明此方法可以带来更卓越的性能.
UDA 模型如下:
与其他基于一致性原则的模型类似, UDA 的最终损失函数也由两部分组成:
- 1.带标签样本的的有监督交叉熵损失 CE loss. E x 1 ∼ p L ( x ) [ − log p θ ( f ∗ ( x 1 ) ∣ x 1 ) ] \mathbb{E}{x_1 \sim p{L(x)}}[-\log p_{\theta}(f^*(x_1)\vert x_1)] Ex1∼pL(x)[−logpθ(f∗(x1)∣x1)]
- 2.在未标记数据上, 对数据进行增强处理后的预测结果 p ( y θ ∣ x ^ ) p(y_{\theta}\vert \hat{x}) p(yθ∣x^) 与增强前的预测结果 p θ ~ ( y ∣ x ) p_{\tilde{\theta}}(y\vert x) pθ
(y∣x) 之间的一致性惩罚 loss. E x 2 ∼ p U ( x ) E x ^ ∼ q ( x ^ ∣ x 2 ) [ C E ( p θ ~ ( y ∣ x 2 ) ∣ ∣ p θ ( y ∣ x ^ ) ) ] \mathbb{E}{x_2\sim p{U(x)}} \mathbb{E}{\hat{x}\sim q(\hat{x}\vert x_2)}[CE(p{\tilde{\theta}}(y\vert x_2)\vert\vert p_{\theta}(y\vert \hat{x}))] Ex2∼pU(x)Ex^∼q(x^∣x2)[CE(pθ(y∣x2)∣∣pθ(y∣x^))]
UDA 针对不同任务有不同的数据增强策略
- RandAugment for Image Classification. 使用一种名为 RandAugment 的数据增强方法, 该方法受到 AutoAugment 的启发. AutoAugment 使用一种搜索方法将 Python 图像库(PIL)中的所有图像处理转换结合起来, 以找到一个好的增强策略. 在 RandAugment 中, 不使用搜索, 而是从 PIL 中的同一组增强变换中统一采样. 换句话说, RandAugment 更简单, 不需要标记数据, 因为不需要搜索最优策略.
- Back-translation for Text Classification. 当用作扩充方法时, 回译(Back-translation)是指将语言 A 中的现有示例 x x x 翻译成另一种语言 B, 然后将其翻译回 A 以获得扩充示例 x ^ \hat{x} x^ 的过程. 回译可以生成不同的释义, 同时保留原始句子的语义, 从而显着提高问答的性能. 如下图所示. 论文的案例中, 使用 Back-translation 来解释文本分类任务的训练数据.

- Word replacing with TF-IDF for Text Classification. 虽然回译擅长维护句子的全局语义, 但对保留哪些单词几乎没有控制. 这个要求对于主题分类任务很重要, 因此, 用低 TF-IDF 值替换.
版权归原作者 码侯烧酒 所有, 如有侵权,请联系我们删除。