去除多重共线性的5种方法，你学废了嘛？

什么是多重共线性呢?

就是回归模型多个特征之间具有很强的相关性。

多重共线性，听起来很就很严重，其实没有很大的危害，只是容易过拟合，或者导致模型无法解释。尤其是在实际项目中，我们需要解释模型的特征对目标变量的影响时，最好要消除多重共线性。

本文就说说怎么去除多重共线性，这里随手找到一份数据，是“快乐星球指数”，显示不同国家国民的幸福指数。

选取的特征有多个维度：寿命，福利，生态碳足迹，GDP，人口等，假如我们需要预测HappyPlanetIndex，而且模型需要可解释，那么怎么选择特征呢？

这里列出5种方法去除共线性特征：

目录

本文技术工具来自技术群小伙伴的分享，想加入按照如下方式

目前开通了技术交流群，群友已超过3000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友
方式①、添加微信号：dkl88191，备注：来自CSDN+技术交流
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群+CSDN

file='data/hpi.csv'
df = pd.read_csv(file)
feature_cols=['AverageLifeExpectancy','AverageWellBeing','HappyLifeYears','Footprint','InequalityOfOutcomes','InequalityAdjustedLifeExpectancy','InequalityAdjustedWellbeing','GDPPerCapita','Population','HappyPlanetIndex']
num_df = df[feature_cols]

定性分析

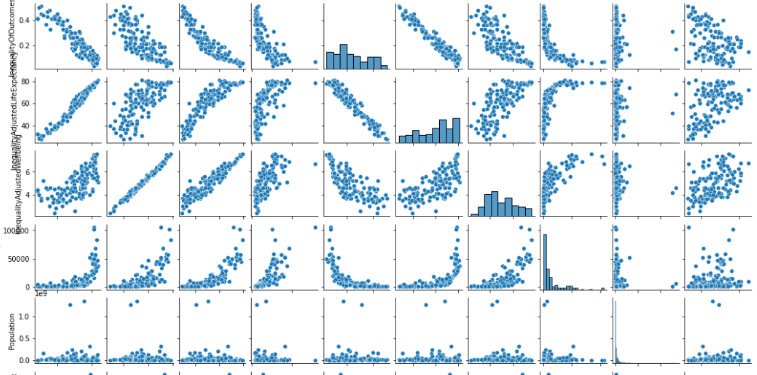
该方法用于定性分析，画出散点图，可以直观的看到每两个特征对的相关性。

如果出现一条完美线性直线，那就保留一个特征即可。

如果相关性太强，也可以只保留一个。

g= sns.pairplot(num_df)

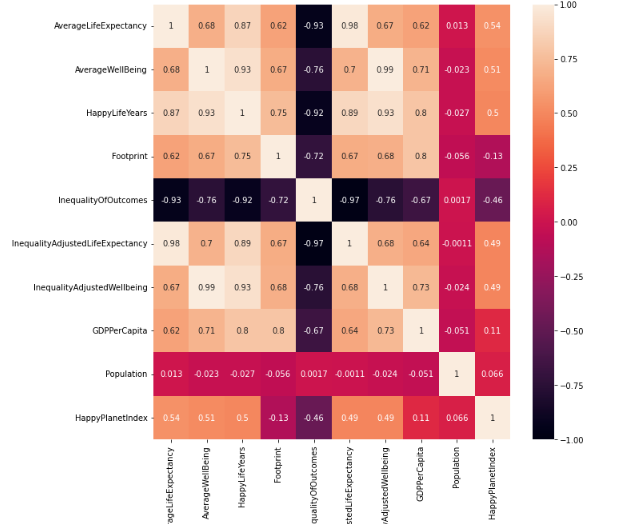
相关系数热力图

这里就是定量分析了，我们可以设定一个阈值，比如0.6。

当相关系数的绝对值大于这个阈值的时候，我们就认定为多重共线性，可以多选一。

fig, ax = plt.subplots(figsize=(10,10)) 
heatmap = sns.heatmap(num_df.corr(), vmin=-1, vmax=1, annot=True,ax=ax)

方差膨胀系数VIF

方差膨胀系数(variance inflation factor，VIF)是衡量多元线性回归模型中复 (多重)共线性严重程度的一种度量。它表示回归系数估计量的方差与假设自变量间不线性相关时方差相比的比值。怎么计算呢？假如我们有5个特征，我们可以用其中的4个特征，去拟合最后一个特征，如果拟合的效果越好（r方越接近100%），那么说明这4个特征里面有“近亲”。

1/（1- R2）就是VIF。

• 经验值来看，VIF大于1小于5，一般可以人为没有多重共线性问题。
• 如果是大于5，小于10，勉强接受。
• 如果大于10，那就要考虑删除一些特征了。

可以直接调用statsmodels模块里面的variance_inflation_factor函数直接计算VIF.

但是这个VIF计算会有bug，因为statsmodels的线性回归算法默认不包含截距信息（intercept)，从而导致VIF计算偏大。

所以建议采用修正版的计算公式，这里我写了两个版本，一个是基于sklearn的，一个是基于statsmodels的。

defvariance_inflation_factor_sm_corr(exog, exog_idx):
    k_vars = exog.shape[1]
    exog = np.asarray(exog)
    x_i = exog[:, exog_idx]
    mask = np.arange(k_vars)!= exog_idx
    x_noti = exog[:, mask]
    r_squared_i = OLS(x_i, sm.add_constant(x_noti)).fit().rsquared
    vif =1./(1.- r_squared_i)return vif

defvariance_inflation_factor_sklearn(exog, exog_idx):
    k_vars = exog.shape[1]
    exog = np.asarray(exog)
    x_i = exog[:, exog_idx]
    mask = np.arange(k_vars)!= exog_idx
    x_noti = exog[:, mask]
    r_squared_i = LinearRegression(fit_intercept=True).fit(x_noti, x_i).score(x_noti, x_i)
    vif =1./(1.- r_squared_i)return vif

defcalc_vif(df,method='all'):    
    vif_data = pd.DataFrame()
    vif_data["feature"]= df.columns

    if method =='sm_corr':
        vif_data["VIF"]=[variance_inflation_factor_sm_corr(df.values, i)for i inrange(len(df.columns))]elif method =='sklearn':
        vif_data["VIF"]=[variance_inflation_factor_sklearn(df.values, i)for i inrange(len(df.columns))]elif method =='sm':
        vif_data["VIF"]=[variance_inflation_factor(df.values, i)for i inrange(len(df.columns))]else:
        vif_data["VIF_sm_corr"]=[variance_inflation_factor_sm_corr(df.values, i)for i inrange(len(df.columns))]
        vif_data["VIF_sklearn"]=[variance_inflation_factor_sklearn(df.values, i)for i inrange(len(df.columns))]
        vif_data["VIF_sm"]=[variance_inflation_factor(df.values, i)for i inrange(len(df.columns))]return vif_data

calc_vif(num_df,method='all')

PCA分析

有一种消除多重共线性的方法是采用PCA分析，但是缺点也是明显了，PCA得到的已经不是原有的特征了，更不利于模型的解释。

pca = PCA(n_components=4)
pca.fit(sel_df)
percent_var_explained = pca.explained_variance_/(np.sum(pca.explained_variance_))
cumm_var_explained = np.cumsum(percent_var_explained)

基于相关系数的迭代法

这个思路很简单，就是基于相关系数，优先选取最小的一对特征，然后去除和它们相关的特征，直至筛选完所有的特征。这里我写了一个函数，用于迭代。

defget_best_feature_couple(df,threshold=0.8):
    corr_matrix = df.corr().abs()
    best_couple = df.corr().abs().stack().idxmin()
    best_value = df.corr().abs().min().min()if best_value <threshold:
        high_corr_col =[]for i in best_couple:
            c = corr_matrix[i]
            high_corr_col +=list(c[c>threshold].index)else:
        best_couple =[]
        high_corr_col =[]
    low_corr_col =[i for i in df.columns if i notin high_corr_col]return best_couple,low_corr_col

deffeature_selection_by_corr(df,corr_threshold=0.4):
    mask =[]whileTrue:
        best_couple,low_corr_col = get_best_feature_couple(df,threshold=corr_threshold)iflen(best_couple)>0:
            mask += best_couple
        iflen(low_corr_col)>=2:
            df = df[low_corr_col]eliflen(low_corr_col)==1:
            mask += low_corr_col
            breakelse:breakreturn mask

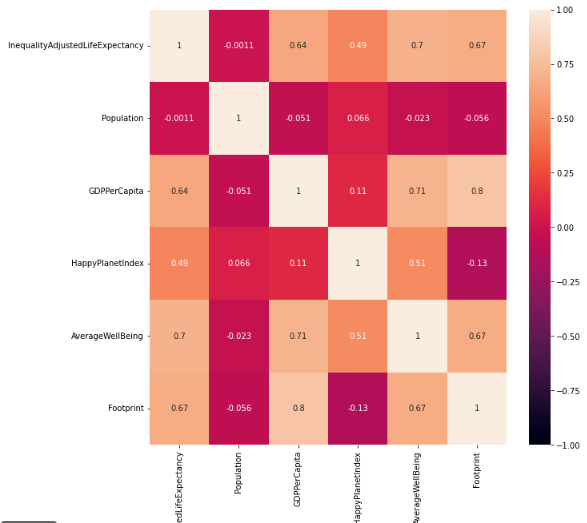
feature_cols = feature_selection_by_corr(num_df,corr_threshold=0.8)
fig, ax = plt.subplots(figsize=(10,10)) 
heatmap = sns.heatmap(num_df[feature_cols].corr(), vmin=-1, vmax=1, annot=True,ax=ax)

总结

以上就是对共线性特征筛选的5种方法，学会了吗？