文章目录
参考文章:
跳转
一、标量
标量只有大小概念,没有方向的概念。通过一个具体的数值就能表达完整。
比如:重量、温度、长度、提及、时间、热量等都数据标量。
百度百科和维基百科
百度百科版本: 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,而没有方向,部分有正负之分。物理学中,标量(或作纯量)指在坐标变换下保持不变的物理量。用通俗的说法,标量是只有大小,没有方向的量。查看详情
维基百科版本: 标量是一个的元素字段,其用于定义一个向量空间。由多个标量描述的量,例如具有方向和幅度,被称为矢量。在线性代数,实数或场的其它元素被称为标量,并涉及到在载体通过的操作的向量空间标量乘法,其中载体可以由多个以产生另一矢量相乘。更一般地,可以通过使用任何字段而不是实数来定义向量空间,例如复数。然后该向量空间的标量将成为相关字段的元素。查看详情
二、向量
向量主要有2个维度:大小、方向。
大小:箭头的长度表示大小
方向:箭头所指的方向表示方向
向量的四种表示方法
代数表示
一般印刷用黑体的小写英文字母(a、b、c等)来表示,手写用在a、b、c等字母上加一箭头(→)表示,如
a
⃗
\vec{a}
a、
b
⃗
\vec{b}
b、
c
⃗
\vec{c}
c。
几何表示
向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。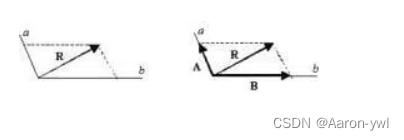
坐标表示
在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i,j作为一组基底。a为平面直角坐标系内的任意向量,以坐标原点O为起点P为终点作向量a。由平面向量基本定理可知,有且只有一对实数(x,y),使得a=xi+yj,因此把实数对(x,y)叫做向量a的坐标,记作a=(x,y)。这就是向量a的坐标表示。其中(x,y)就是点 P 的坐标。向量a称为点P的位置向量。
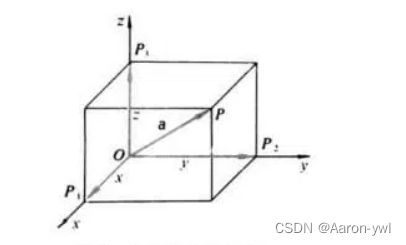
当然,对于多维的空间向量,可以通过类推得到。
矩阵表示
如
a
=
[
x
y
]
a = \begin{bmatrix} x \\ y \end{bmatrix}
a=[xy]
b
=
[
x
y
z
]
b = \begin{bmatrix} x \\ y \\ z \end{bmatrix}
b=⎣⎡xyz⎦⎤
百度百科和维基百科
百度百科版本: 在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
向量的记法:印刷体记作黑体(粗体)的字母(如a、b、u、v),书写时在字母顶上加一小箭头“→”。 如果给定向量的起点(A)和终点(B),可将向量记作AB(并于顶上加→)。在空间直角坐标系中,也能把向量以数对形式表示,例如xOy平面中(2,3)是一向量。查看详情
维基百科版本: 向量空间(也称为线性空间)是称为对象的集合的载体,其可被添加在一起,并乘以由数字(“缩放”),所谓的标量。标量通常被认为是实数,但是也存在标量乘以复数,有理数或通常任何字段的向量空间。向量加法和标量乘法的运算必须满足下面列出的某些要求,称为公理。
欧几里德向量是向量空间的一个例子。它们代表物理量,诸如力:任何两个力(同一类型的)可被添加,以产生第三和的相乘力矢量由一实数乘法器是另一个力矢量。同样,但在更几何意义上,表示平面或三维空间中的位移的矢量也形成矢量空间。向量空间中的向量不一定必须是箭头状对象,因为它们出现在上述示例中:向量被视为具有特定属性的抽象数学对象,在某些情况下可以将其视为箭头。
向量空间是线性代数的主题,并且通过它们的维度很好地表征,粗略地说,它指定了空间中独立方向的数量。无限维向量空间在数学分析中自然出现,作为函数空间,其向量是函数。这些向量空间通常具有附加结构,其可以是拓扑结构,允许考虑接近度和连续性问题。在这些拓扑中,由规范或内积定义的拓扑更常用,因为它具有距离概念两个向量之间。特别是Banach空间和Hilbert空间的情况,这是数学分析的基础。查看详情
三、矩阵
矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:
A
=
[
a
11
a
12
.
.
.
a
1
n
a
21
a
22
.
.
.
a
2
n
a
31
a
32
.
.
.
a
3
n
.
.
.
.
.
.
.
.
.
.
.
.
a
m
1
a
m
2
.
.
.
a
m
n
]
A = \begin{bmatrix} a_{11}&a_{12}&...&a_{1n}\\ a_{21}&a_{22}&...&a_{2n}\\ a_{31}&a_{32}&...&a_{3n}\\ ...&...&...&...\\ a_{m1}&a_{m2}&...&a_{mn} \end{bmatrix}
A=⎣⎡a11a21a31...am1a12a22a32...am2...............a1na2na3n...amn⎦⎤
百度百科和维基百科
百度百科版本: 在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵,例如稀疏矩阵和准对角矩阵,有特定的快速运算算法。关于矩阵相关理论的发展和应用,请参考矩阵理论。在天体物理、量子力学等领域,也会出现无穷维的矩阵,是矩阵的一种推广。查看详情
维基百科版本: 在数学中,矩阵是一个矩形 阵列的数字,符号,或表达,排列成行和列。例如,下面矩阵的尺寸是2×3(读“两乘三”),因为有两行三列:
如果它们具有相同的大小(每个矩阵具有与另一个相同的行数和相同的列数),则可以逐个元素地添加或减去两个矩阵(参见符合矩阵)。然而,矩阵乘法的规则是,只有当第一列中的列数等于第二列中的行数时,两个矩阵才能相乘(即,内部维度相同,n为(m × n)) – 矩阵乘以(n × p)矩阵,得到(m × p)-矩阵。反过来没有产品,第一个暗示矩阵乘法不是可交换的。任何矩阵都可以通过其相关字段中的标量逐个元素相乘。 在各个项米 × Ñ矩阵甲,经常表示为一个我,Ĵ,其中我和Ĵ通常会发生变化,从1至米和 Ñ分别被称为它的元素或条目。
为了方便地表示矩阵运算结果的元素,元素的索引通常附加到带括号或括号的矩阵表达式中; 例如:(AB)i,j指矩阵乘积的元素。在上下文中抽象指数表示法这个含糊不清也指整个矩阵乘积。 查看详情
四、张量
张量有很多种定义的方式,这里只讨论人工智能领域里的概念。
在人工智能领域,定义比较简单,TensorFlow是这么定义的:A tensor is a generalization of vectors and matrices to potentially higher dimensions.
简单翻译过来就是:张量是多维数组,目的是把向量、矩阵推向更高的维度。
百度百科和维基百科
百度百科版本: 张量(tensor)理论是数学的一个分支学科,在力学中有重要应用。张量这一术语起源于力学,它最初是用来表示弹性介质中各点应力状态的,后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要,在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广,矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。查看详情
维基百科版本: 在数学中,张量是一种几何对象,它以多线性方式将几何向量,标量和其他张量映射到结果张量。因此,通常在基础物理和工程应用中已经使用的矢量和标量本身被认为是最简单的张量。另外,来自提供几何矢量的矢量空间的双空间的矢量也被包括作为张量。在这种情况下,几何学主要是为了强调任何坐标系选择的独立性。查看详情
五、标量、向量、矩阵、张量的关系
这4个概念是维度不断上升的,我们用点线面体的概念来比喻解释会更加容易理解:
- 点——标量(scalar)
- 线——向量(vector)
- 面——矩阵(matrix)
- 体——张量(tensor)

版权归原作者 Aaron-ywl 所有, 如有侵权,请联系我们删除。