毕业设计-基于MATLAB的含噪语音信号降噪处理方法的研究与实现

前言

📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。

🚀对毕设有任何疑问都可以问学长哦!

选题指导: https://blog.csdn.net/qq_37340229/article/details/128243277

大家好,这里是海浪学长毕设专题,本次分享的课题是

🎯基于MATLAB的含噪语音信号降噪处理方法的研究与实现

课题背景和意义

随着互联网信息技术的不断发展与普及， 语 音依然是人类沟通、 交流传递信息的重要载体。 语音信号处理是一个新兴的交叉学科， 是语音 和数字信号处理的两个学科的结合产物， 即综合 运用数字信号处理技术对语音信号进行处理 。 随着互联网、 信息技术的发展， 除了人们之间自 然语言的交流，人机对话以及智能领域也都使用 语音。 语音信号在采集、 存储、 传输过程中会不 可避免的受到噪声和干扰的污染， 当语音信号淹 没在噪声中时， 人们很难得到有用的信息， 给语 音信号的处理带来不便 。 因此，加强语音信号降噪研究，对改善语音信号质量，提高语音信号清晰度，具有重要的现实意义。利用计算机采集 语音信号， 在 ＭＡＴＬＡＢ 软件环境下对原始语音信 号以及加噪后的语音信号进行时域、 频域分析， 设计 ＩＩＲ 数字滤波器对加噪语音信号进行滤波降 噪处理， 仿真滤波后语音信号的时域、 频域波形 图， 对比原始语音信号， 分析含噪语音信号降噪处理结果。

实现技术思路

一、设计思路

利用电脑采集一段音乐信号， ＭＡＴＬＡＢ 可读 . ｗａｖ 文件， 保存为 . ｗａｖ 文件。 对采集到的音 乐信号进行时域、 频域分析， 输出时域波形以及 幅度谱。 音乐信号的频率范围一般在几十赫兹到 ２０ｋＨｚ， 最高频率不会超过 ２０ｋＨｚ， 故采用抽样频 率为 ４４. １ｋＨｚ， 抽样频率大于最高频率的两倍， 信号不存在混叠误差。 再对采集到的原始音乐信 号人为的加入高频噪音， 产生含噪音乐信号， 模 拟语音信号被噪声污染。 利用双线性变换法设计 合适的数字低通滤波器， 对信号进行滤波， 并仿真得到时域、 频域波 形图， 分析结果。

二、ＩＩＲ 数字滤波器的设计原理

数字滤波器是能按性能指标要求完成信号滤 波处理功能的数字系统。 按单位脉冲响应长度可 分为无限长单位脉冲响应滤波器即 ＩＩＲ 滤波器和 有限长单位脉冲响应即 ＦＩＲ 滤波器。 线性时不 变系统用系统函数表示为：

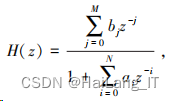
其中 ａ１ ， …， ａＮ 中至少有一项不为零时， 系统函 数采 用 部 分 分 式 展 开 法 可 表 示 为：

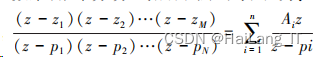
对系统 函数进行拉普拉斯逆变换， 得到相应的单位脉冲 响应：

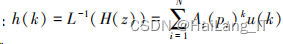
单位脉冲响应长度无限， 故被称为 ＩＩＲ 无限长单 位脉冲响应滤波器。 相应的 ＦＩＲ 有限长单位脉冲 响应长度有限， 一般实现相同 的指标性能， ＦＩＲ 数字滤波器所需阶数远大于 ＩＩＲ 数字滤波器。 ＩＩＲ 数字滤波器适合处理对相位要求不高的信号， 如 脉搏信号、 语音信号等。

**模拟滤波器 **

由于模拟滤波器的相关理论和设计技巧已经很成熟， 并且有典型的模板和闭合形式的公式。 但是相比于模拟滤波器， 数字滤波器具有精度高、 灵活性大的优点， 使用更灵活， 应用范围更广。 基于已经发展成熟的模拟滤波器设计无限长 单位冲激响应数字滤波器 （ ＩＩＲ）。

常用的典型模拟滤波器的模板有巴特沃斯型 滤波器、 切比雪夫型滤波器、 椭圆型滤波器。 其 中， 滤波器按功能分类有低通滤波器、 高通滤波 器、 带通滤波器、 带阻滤波器， 其中低通滤波器 是最基础的， 其他功能的滤波器可以采用频率变 换法转换即由低通滤波器转换得到。。 巴特沃斯模 拟低通滤波器的频域特性表示为：

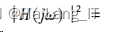
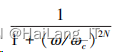
其中， Ｎ 代表滤波器的阶数， 阶 数越高， 性能越好， 实现成本高， ωｃ 表示 ３ｄＢ 截 频。 通过改变 Ｎ、 ωｃ 可以得无数个巴特沃斯滤波 器。 根据 （ωｐ， Ａｐ） 、 （ωｓ， Ａｓ） 可以确定：

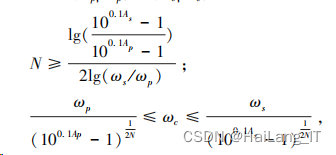
其幅频特性如图所示：

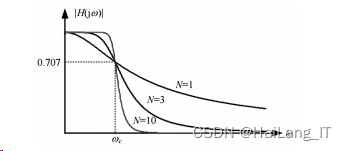
切比雪夫 １ 型模拟低通滤波器的频域特性表示为：

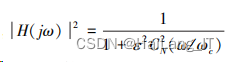
其中， Ｎ 表 示滤波器的阶数， ωｃ 表示通带截频， ε 表示通带波 纹。 １ 型的切比雪夫滤波器的通带有波纹， 波纹由 通带衰耗 Ａｐ 决定； 切比雪夫 １ 型模拟低通滤波器 其幅频特性如下图所示。 切比雪夫 ２ 型滤波器 通带没有纹波， 但是阻带有纹波。

椭圆型滤波器通带、 阻带都有纹波， 椭圆型 模拟低通滤波器的频域特性表示为：

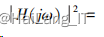
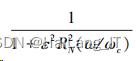
椭圆型滤波器通带、 阻带都有纹波， 椭圆型 模拟低通滤波器的频域特性表示为：

双线性变换法设计

ＩＩＲ 数字低通滤波器 任何实际的模拟滤波器的带宽都不是绝对有 限的， 所以采用脉冲响应不变法进行离散化设计 数字滤波器时， 会产生频谱混叠效应， 为了克服 脉冲响应不变法所产生的频谱混叠效应， 可以采 用凯塞和戈尔登提出的双线性变换法， 也可以称 为改进的脉冲响应不变法， 其基本思想是首先将 非带限的模拟滤波器通过映射压缩使最高频率为 π／ Ｔ 的带限模拟滤波器 。 模拟频率 ω 与数字频率 Ω 的关系为：

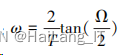
再将通过压缩得到的带限模拟滤波器通过脉 冲响应不变法映射到 ｚ 平面， 映射关系为：

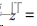
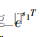
进一步得到 ｓ 平面和 ｚ 平面的映射关系为：

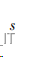
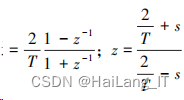
设计步骤如图所示：

ＩＩＲ 数字滤波器的频率转换

实际中使用的数字滤波器除了低通滤波器以 外， 通常还有高通、 带通、 带阻等 ＩＩＲ 数字滤波 器。 为满足需要， 首先设计一个满足指标要求的 模拟原型低通滤波器， 通过频率转换成所需要的 各种不同功能的滤波器， 最后离散化， 采用能够 克服频谱混叠的双线性变换法设计成相应的数字 滤波器。 模拟域频率转换具体指标如表所示：

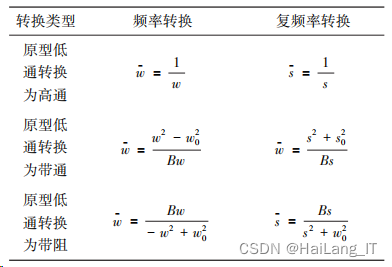
三、语音信号的采集、 含噪语音信号的分析处理

语音信号的采集及分析

六号， 固定行距 １０ 磅利用电脑采集一段音乐 信号， 保 存 为 “ 音 乐 信 号 . ｗａｖ ” 文 件。 调 用 ＭＡＴＬＡＢ 软件数据库中 ａｕｄｉｏｒｅａｄ 函数可以读取采 集的原始语音信号， 进行时域分析， 输出时域波 形如图

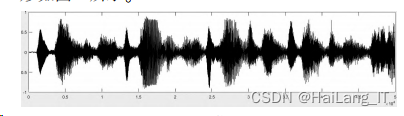
调用 ｆｆｔ （ ｘ ） 函数对语音信号进行频谱分析 输出信号频谱， 绘制原始语音信号幅度谱如图所示。

加噪语音信号的产生及分析

将采集到的原始语音信号叠加上高频余弦噪 声信号， 噪声信号如图所示。

因为分辨率的原 因， 看起来就是一整体，高频余弦波形：

人为加入高频余弦信 号模拟被噪声污染的含噪语音信号， 并进行时域、 频域分析， 仿真得到时域波形、 频谱如图，余弦信号频谱 ：

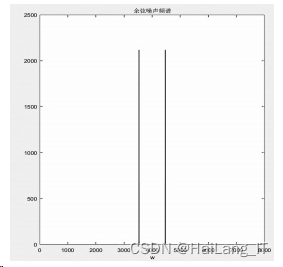
从仿真结果可以看出含噪语音信号时域波形 发生很大的变化， 含噪语音信号的频谱上明显比 原语音信号频谱多了余弦高频分量。

ＭＡＴＬＡＢ 辅助设计、 仿真结果

根据语音信号的分析采用双线性变化法设计 满足指标 ｗｐ ＝ ０. ６５π ｒａｄ、 ｗｓ ＝ ０. ７５π ｒａｄ， Ａｐ ＝ ５， Ａｓ ＝ ２０ 的巴特沃斯数字系统滤波器。ｗｐ ＝ ０. ６５；％通带边界频率 ｗｓ ＝ ０. ７５；％阻带边界频率

［Ｎ１， Ｗｃ］ ＝ ｂｕｔｔｏｒｄ （ ｗｐ， ｗｓ， Ａｐ， Ａｓ， ＇ｓ
＇）；％Ｒｐ、 Ｒｓ 分别为滤波器的通带最大衰减和阻带
最小衰减 （ｄＢ）
［Ｂ， Ａ］ ＝ ｂｕｔｔｅｒ （Ｎ１， Ｗｃ， ＇ｓ＇）；％计算滤波
器系统分子分母多项式系数
［ｎｕｍｄ， ｄｅｎｄ］ ＝ ｂｉｌｉｎｅａｒ （ Ｂ， Ａ， １）％ 双线
性变换法
［Ｈ， Ｗ］ ＝ ｆｒｅｑｚ （ ｎｕｍｄ， ｄｅｎｄ）；％生成巴特
沃斯低通滤波器
ｆｉｇｕｒｅ （ ４ ）， ｐｌｏｔ （ Ｗ／ ｐｉ， ａｂｓ （ Ｈ ） ）； ｔｉｔｌｅ
（＇ｄｉｇｉｔａｌ ｂｕｔｔｅｒ ｆｉｌｔｅｒ ＇）；
％巴特沃斯滤波器对 ｙ１ 进行滤波
Ｆ＿ ｙ１ ＝ ｆｉｌｔｅｒ （ｎｕｍｄ， ｄｅｎｄ， ｙ１）；
ｆｆｔ＿ Ｆ＿ ｙ１ ＝ ｆｆｔ （Ｆ＿ ｙ１， Ｎ）；％滤波后音乐信
号傅里叶变换
ｓｏｕｎｄ （Ｆ＿ ｙ１， ｆｓ）；
ｆｉｇｕｒｅ （ ５）， ｓｕｂｐｌｏｔ （ １， ２， １）， ｐｌｏｔ （ Ｆ ＿
ｙ１）， ｔｉｔｌｅ （＇Ｍｕｓｉｃ ｓｉｇｎａｌ ａｆｔｅｒ ｌｏｗ－ｐａｓｓ ｆｉｌｔｅｒｉｎｇ＇）％
显示叠加噪声后音乐信号
ｓｕｂｐｌｏｔ （ １， ２， ２ ）， ｐｌｏｔ （ ａｂｓ （ ｆｆｔ ＿ Ｆ ＿
ｙ１） ）， ｔｉｔｌｅ （＇ｆｒｅｑｕｅｎｃｙ ｄｉｓｔｒｉｂｕｔｉｏｎ ｏｆ ｍｕｓｉｃ ｓｉｇｎａｌ
ａｆｔｅｒ ｌｏｗ ｐａｓｓ ｆｉｌｔｅｒｉｎｇ＇）；

经滤波器降噪后的语音信号时域波形及频谱图如图所示。

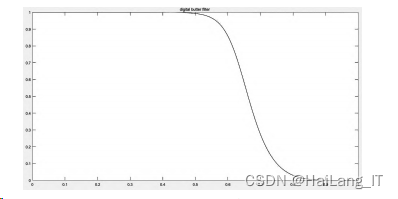
滤波后语音信号波形：

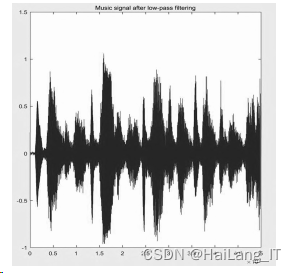
滤波后语音信号频谱 ：

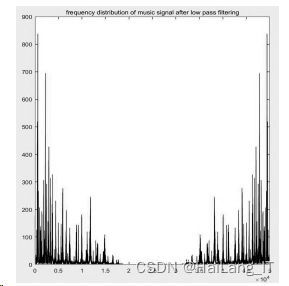
从仿真结果可以看到加入噪声的语音信号经 滤波后余弦分量的频谱被滤除。 同时利用借助 ＭＡＴＬＡＢ 软件数据库中 ｓｏｕｎｄ （ ｓ） 函数回放滤波后的音乐信号， 尖锐的噪声明显消失， 说明采用数字低通滤波器后滤除了信号中的高频分量。

实现效果图样例

语音识别之降噪技术：

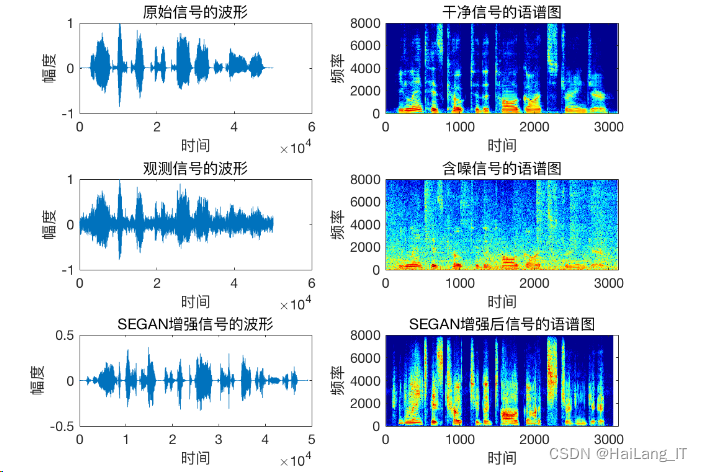
我是海浪学长,创作不易,欢迎点赞、关注、收藏、留言。

毕设帮助，疑难解答，欢迎打扰！

最后