0
0

机器学习 | sklearn库

一、样本及样本的划分

1.1 样本划分

从数据中学习并得到模型的过程称为“学习”或“训练”，这个过程通过执行某个学习算法来完成。因为机器学习需要从样本中进行学习，所以机器学习中也有样本的概念，与统计学相比，根据样本在学习中所起的作用，机器学习中的样本经常划分为如下3类：

  • 训练集：用于模型拟合的数据样本，即建立模型使用的样本集。
  • 验证集：是模型训练过程中单独留出来的样本集，可以用于调整样本模型的超参数，以及对模型的能力进行初步评估。
  • 测试集：用来测试模型在预测未知样本时的准确率，即评估最终模型的泛化能力。所谓泛化能力，是指机器学习模型对新鲜样本的适应能力。泛化能力不能作为调参、选择特征等与算法相关的选择依据。

一般，在做预测分析时会将样本划分为两部分：一部分是训练集数据，用于构建模型；另一部分是测试集 数据，用于检验模型。但有时候在模型的构建过程中也需要检验模型，辅助模型构建，这时就需要再划分出一部分作为验证集，因此验证集是可选的。

训练集的规模远大于验证集和测试集。在小样本机器学习中，训练集、测试集、验证集的比例一般为7:1:2，而在大样本机器学习中，训练集所占的比例一般为99%左右，验证集和测试集占1%左右。

机器学习的步骤如下：

（1）使用训练集中的数据训练模型，得到一个初步的模型。

（2）使用验证集验证模型的有效性，并调整参数使模型尽可能地有效，这一步会得到最终的模型。

（3）使用测试集测试最终模型的准确率。方法是，先不看测试集中的类别属性，将测试集中的样本特征集输入机器学习模型中，看该模型输出的类别属性与测试集中的实际类别属性差异有多大。差异越小，说明模型的有效性越高。测试集只是测试模型的准确率。

1.2 划分样本的方法

机器学习的样本划分可以采用train_test_split()函数，也可以采用交叉验证的方法。

sklearn提供了一个将数据集切分称训练集和测试集的函数train_test_split()。该函数默认把数据集的75%作为训练集，把数据集的25%作为测试集。也可以用test_size设置测试集所占的比例，代码如下：

from sklearn.model_selection import train_test_split
#将样本划分为训练集和测试集，其中测试集占20%，random_state表示随机因子
Xtrain,Xtest,Ytrain,Ytest=train_test_split(X,y,test_size=0.2,random_state=420)

如果是大数据集，使用train_test_split()函数的划分方法没有问题，如果是小数据集，将其划分为两或三份会导致训练样本量的不足。因此，对于小数据集，通常使用交叉验证的方法。交叉验证有许多版本，一般使用k折交叉验证。

交叉验证一般去十折交叉验证，将样本划分为k个子集，每个子集均作为一次测试集，其余的作为训练集。交叉验证重复k次，每次选择一个子集作为测试集，并将k次的平均交叉验证识别作为结果。

sklearn提供了一个对样本集进行交叉验证的函数cross_val_predict()。该函数有4个参数，其中，cv表示迭代次数。代码如下：

from sklearn.model_selection import cross_val_predict
predicted=cross_val_predict(clf,iris.data,iris.target,cv=10)
metrics.accuracy_score(iris.target,predicted)  #交叉验证的结果

其中，clf是一个分类器，iris.data是特征数据，iris.target是类别数据。

在使用交叉验证时计算量会增加很多，对于处理大数据集是个负担。可以通过查看交叉验证中的train_score和test_score，判断模型是否过拟合或者欠拟合。

更详细的交叉验证

二、导入或创建数据集

传统的机器学习任务从开始到建模的一般流程是获取数据\rightarrow数据预处理\rightarrow训练建模\rightarrow模型评估\rightarrow预测、分类。

在sklearn中要获取或创建样本数据有以下三种方法：

2.1 导入sklearn自带的样本数据集

在sklearn的datasets模型中提供了一些样本训练数据，可以使用这些数据进行分类、聚类或进行回归分析，以方便创建机器学习模型。这些数据集存放在D:\Anaconda3\Lib\site-packages\sklearn\datasets\data目录下。导入这些自带的样本数据集需要使用专门的调用函数，如下表所示：

sklearn自带的样本数据集
数据集名称调用函数适用算法数据规模（行列）数据集大小波士顿房价数据集load_boston()回归50613小鸢尾花数据集load_iris()分类1504小糖尿病数据集load_diabetes()回归44210小体能训练数据集load_linnerud()手写数字图像数据集load_digits()分类562064小Olivetti脸部图像数据集fetch_olivetti_faces降维4006464大新闻分类数据集fetch_20newsgroups()分类大带标签的人脸数据集fetch_lfw_people()分类、降维大路透社新闻语料数据集fetch_rcv1()分类80441447236大
上表的函数默认参数都为空，除了默认参数之外，还包括以下参数：

  • return_X_y：表示是否返回target（即类别属性）。默认为False，只返回data（即特征属性）。
  • n_class：表示返回数据的类别数，如n_class=5，则返回0~4含有5个类别的样本。

例：导入Iris数据集并输出该数据集的特征属性和类别标签。

from sklearn.datasets import load_iris
dataSet=load_iris()  #导入Iris数据集
data=dataSet['data']  #data是特征数据集
label=dataSet['target']  #label是类别标签
feature=dataSet['feature_names']  #特征的名称
target=dataSet['target_names']  #标签（类别）的名称
print(feature,target)

程序运行结果如下：

['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] ['setosa' 'versicolor' 'virginica']

由结果可知该数据集是一个有4个特征属性的三分类问题的数据集。

2.2 利用sklearn生成随机的数据集

在sklearn的datasets模块中有很多类似make_<name>的函数，用来自动生成具有各种形状分布的数据集，这些函数可以“无中生有”地生成随机数据。常用的函数如下：

  • make_circles()：生成环形数据，产生二维二元分类数据集，可以为数据集添加噪声，还可以为二元分类器产生一些环形判决界面的数据。
  • make_moons()：生成月亮形（半环形）数据，其他特征与make_circles()相同。
  • make_blobs()：生成多类单标签数据集，为每个类分配一个或多个正态分布（球形）的点集。
  • make_classification()：生成多类单标签数据集，为每个类分配一个或多个正态分布的点集，该函数提供了为数据添加噪声的方式，包括维度相关性、无效特征及冗余特征等。
  • make_guassian_quantiles()：将一个单高斯分布的点击划分为两个数量均等的点集。

例：生成环形、月亮形和球形数据集。

from sklearn.datasets import make_circles
from sklearn.datasets import make_moons
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(12,4))
plt.subplot(131)
x1,y1=make_circles(n_samples=1000,factor=0.5,noise=0.1)
#factor表示里圈与外圈的距离之比，每圈共有n_samples/2个点
plt.scatter(x1[:,0],x1[:,1],marker='o',c=y1)
plt.subplot(132)
x1,y1=make_moons(n_samples=1000,noise=0.1)
plt.scatter(x1[:,0],x1[:,1],marker='o',c=y1)
plt.subplot(133)
x1,y1=make_blobs(n_samples=100,n_features=2,centers=3)
plt.scatter(x1[:,0],x1[:,1],c=y1);
plt.show()

2.3 读入自己创建的数据集

Pandas是python的一个数据分析库，可以读取和写入文件。使用Pandas不仅可以读取表格型数据，如Excel文件。CSV文件或txt文件等，而且可以将其转换成DataFrame类型的数据结构，然后就可以通过DataFrame进行行和列操作及数据分析等工作了。例如：

import pandas as pd  #导入Pandas库
data=pd.read_excel('D:\\18ds.xlsx')  #读取Excel文件
data2=pd.read_csv('C:\\lr2.xlsx')  #该函数可读取CSV或txt文件
print(data)

三、数据预处理

在机器学习中，获取的原始样本数据往往存在缺失值、重复值等问题，在使用之前必须进行数据预处理。数据预处理没有标准的流程，一般包括：去除唯一属性、处理缺失值、属性编码、数据标准化、特征选择、主成分分析几步。

3.1 数据标准化

对于样本数据来说，首先需要消除样本特征之间不同数量级的影响，而数据标准化就是用来消除不同量级影响的。常用的数据标准化方法有如下两种：

  • min-max标准化（归一化）：对于任意属性A，设minA和maxA分别为属性A中的最小值和最大值，将A中的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x^{'}。其公式为：

新数据=（原数据 - 最小值）/（最大值 - 最小值）

这样标准化后，所有属性都将变成区间[0,1]中的值。

  • Z-score标准化（规范化）：对于任意属性A，将A的原始值x使用Z-score标准化到 x^{'}。Z-score标准化方法适用于属性A总体的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。其公式为：

新数据=（原数据 - 均值）/标准差

均值和标准差都是在样本集中定义的，而不是在单个样本中定义的。标准化是针对某个属性而言的，涉及所有样本在该属性中的值。

3.2 sklearn中的数据标准化函数

sklearn提供了一个专门用于数据预处理的模块sklearn.preprocessing，这个模块中集成了很多数据预处理的方法，包括数据标准化函数，常见的函数如下：
（1）二值化函数binarizer()：将数据根据给定的阈值映射到0和1，其中，阈值默认是0.0。该函数可接受float类型的阈值，数据大于阈值时映射为1，小于等于阈值时映射为0。

例：数据矩阵的二值化举例。

from sklearn.preprocessing import Binarizer
X=[[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]  #数据矩阵
binary=Binarizer()
transformer=binary.fit(X)   #fit does nothing.
transformer.transform(X)
Binarizer(copy=True,threshold=0.0)
print(transformer.transform(X))

结果如下： 

[[1. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]]

说明：
binary=Binarizer()实例化一个阈值为0的二值化对象，transformer=binary.fit(X)使用这个二值化对象的fit()方法去拟合X，返回一个二值化类的实例化对象。注意此时X还没有被二值化，transformer.transform(X)调用二值化对象的transform()方法对X进行二值化，返回二值化后的X。fit()方法和transform()方法也可以合并为一个方法fit_transform()。

（2）归一化函数MinMaxScaler()：将数据均匀地映射到给定的range(min,max)中，默认range为(0,1)。

例：数据矩阵的归一化举例。

from sklearn.preprocessing import MinMaxScaler
data=[[-1,6],[-0.5,2],[0,10],[1,18]]
scaler=MinMaxScaler()
scaler.fit(data)
MinMaxScaler(copy=True,feature_range=(0,1))
print('range的最大值为：',scaler.data_max_)
print('range的最小值为：',scaler.data_min_)
print(scaler.transform(data))

程序的运行结果如下：

range的最大值为： [ 1. 18.]
range的最小值为： [-1.  2.]
[[0.   0.25]
 [0.25 0.  ]
 [0.5  0.5 ]
 [1.   1.  ]]

说明：
scaler=MinMaxScaler()实例化一个最小/最大化对象，scaler.fit(data)计算data的最小值和最大值并返回一个对象。此时可查看此对象属性值 scaler.data_max_，然后用scaler.transform(data)对data进行归一化并返回归一化后的结果。

（3）Z-score标准化函数scale()：通过计算训练集中样本的相关统计量（均值和单位方差）存储均值和标准差，对每个特征单独进行中心化和缩放，使用变换方法测试数据。

标准化有两种实现方式，一种是调用sklearn.preprocessing.scale()函数，另一种是实例化一个sklearn.preprocessing.StandardScaler()对象。后者的好处是可以保存通过训练得到的参数（均值、方差），直接使用sklearn.preprocessing.StandardScaler()对象对测试数据进行转换。

例：数据矩阵的Z-score标准化举例。

from sklearn.preprocessing import StandardScaler
data=[[0,0],[0,0],[1,1],[1,1]]
scaler=StandardScaler()
print(scaler.fit(data))
StandardScaler(copy=True,with_mean=True,with_std=True)
print(scaler.mean_)  #输出均值
print(scaler.var_)  #输出标准差
print(scaler.transform(data))  #标准化矩阵data
print(scaler.transform([[2,2]]))  #标准化新数据

程序运行的结果如下：

StandardScaler()
[0.5 0.5]
[0.25 0.25]
[[-1. -1.]
 [-1. -1.]
 [ 1.  1.]
 [ 1.  1.]]
[[3. 3.]]

3.3 正则化函数Normalizer()

正则化是将每个样本都缩放到单位范数（每个样本的范数为1），如果后面要使用二次型（点积）或者其他核函数计算两个样本之间的相似度，这个方法会很有用。正则化在逻辑回归、支持向量机、神经网络中经常使用。

正则化的主要思想是对每个样本计算其p-范数，然后让该样本中的每个元素除以该范数，这样处理的结果是使处理后的每个样本的p-范数（11-norm或12-norm）等于1。p-范数的计算公式如下：

\left \| X \right \|_{p}=(\sum_{i=1}^{n}|x_{i}|^{p})^{\frac{1}{p}}=(|x_{1}|^{p}+|x_{2}|^{p}+...+{|x_{n}|^{p}})^{\frac{1}{p}}

例：数据矩阵的正则化举例。

from sklearn.preprocessing import Normalizer
X=[[4,1,2,2],[1,3,9,3],[5,7,5,1]]
transformer=Normalizer().fit(X)
print(transformer.transform(X))

程序的运行结果如下：

[[0.8 0.2 0.4 0.4]
 [0.1 0.3 0.9 0.3]
 [0.5 0.7 0.5 0.1]]

四、数据的降维

降维算法中的“降维”，指的是降低特征矩阵中特征的数量。降维的目的是让算法运算更快，效果更好，但其实还有另一个益处：数据可视化。图像和特征矩阵的维度是可以相互对应的，即一个特征对应一个特征向量，对应一个坐标轴。因此，三维及以下的特征矩阵是可以被可视化的。

主成分分析法(PCA)是最常用的一种降维方法，通常用于高维数据集的探索与可视化，还可以用作数据压缩和预处理等。矩阵的主成分就是其协方差矩阵对应的特征向量，按照对应的特征值大小进行排序，最大的特征值就是第一主成分，其次是第二主成分，以此类推。

在sklearn的decomposition模块中，PCA类用来实现主成分分析。

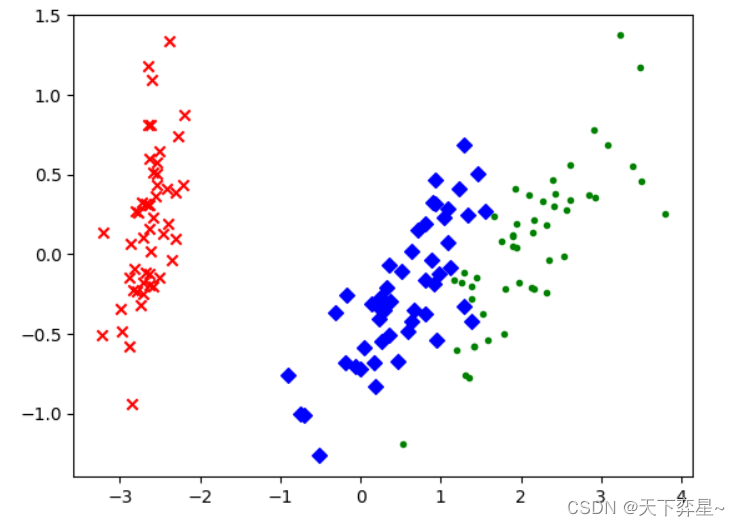
例：用PCA方法对鸢尾花数据进行PCA降维（由四维降成二维）。

import matplotlib.pyplot as plt  #加载Matplotlib用于数据的可视化
from sklearn.decomposition import PCA  #加载PCA算法包
from sklearn.datasets import load_iris
data=load_iris()  #载入Iris数据集
y=data.target
x=data.data
pca=PCA(n_components=2)  #加载PCA算法，设置降维后的维度为2
reduced_x=pca.fit_transform(x)  #对样本的特征属性集进行降维
red_x,red_y=[],[]  #保存第0类样本
blue_x,blue_y=[],[]  #保存第1类样本
green_x,green_y=[],[]  #保存第2类样本
for i in range(len(reduced_x)):  #该数据集有3个类别，因此y[i]=0，1，2
    if y[i]==0:                  #reduced_x[i]表示第i个样本降维后的结果
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])
    elif y[i]==1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')  #可视化
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

标签： 机器学习 sklearn python
本文转载自: https://blog.csdn.net/m0_70452407/article/details/130081508
版权归原作者 天下弈星~ 所有， 如有侵权，请联系我们删除。
登录后发布评论

“机器学习 | sklearn库”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

Visual Studio Code(VS Code)配置C/C++环境

RabbitMQ高效的消息队列中间件原理及实践

RabbitMQ 发布确认高级部分

oracle和hive之间关于sql的语法差异及转换

数据库基础（MySQL）

MySQL：库和表的操作

如何安装Rocky Linux8.5？详细过程及安装包如下

文章导航