排序算法之交换排序（快排的递归，非递归）

**个人主页：欢迎大家光临——>**沙漠下的胡杨

** 各位大帅哥，大漂亮**

如果觉得文章对自己有帮助

可以一键三连支持博主

** 你的每一分关心都是我坚持的动力**

** **

☄：本期重点：快排的递归，非递归和排序的优化

** 希望大家每天都心情愉悦的学习工作。**

书接上回，我们讲过了三种办法的单趟排序的实现，下一步我们就重点讲解快排的递归，非递归和排序的优化。

关于递归会不会影响效率的解释：

递归 现代编译器优化很好，性能已经不是大问题
最大的问题->递归深度太深，程序本身没问题，但是栈空间不够，导致栈溢出，只能改成非递归，改成非递归有两种方式：
1、直接改循环-》斐波那契数列求解

2、树遍历非递归和快排非递归等等，只能用Stack存储数据模拟递归过程

递归版：

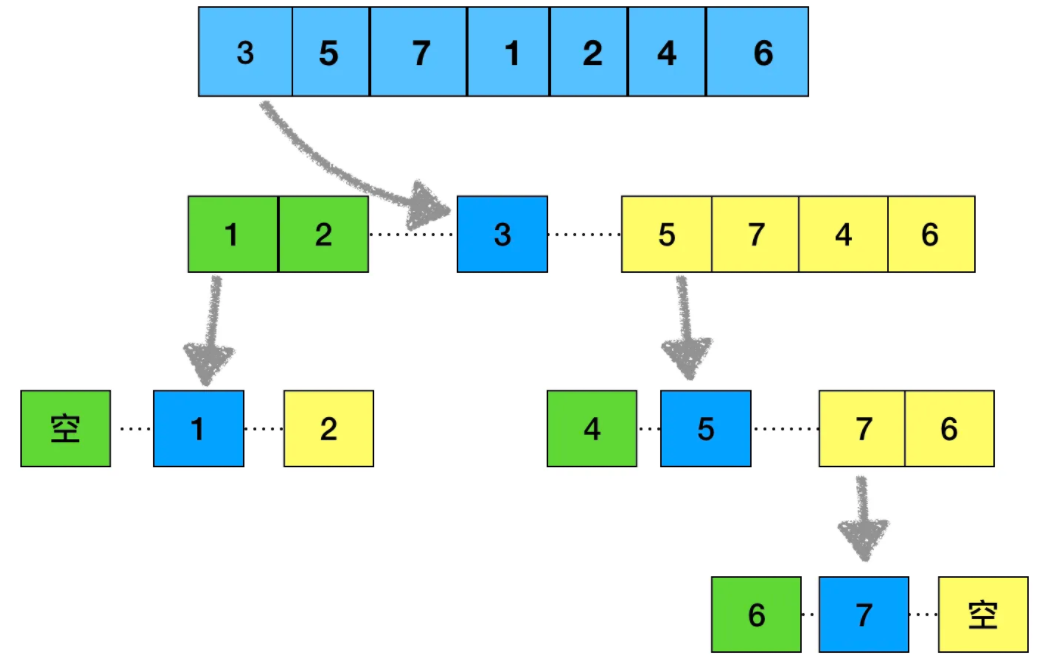
首先我们使用单趟排序把数据分为三部分了，[0,keyi] 和 keyi 以及[keyi+1,keyi]这三部分，那么我们进行递归分析，首先我们递归结束的条件是，当范围内的数据只剩下1个或者没有数据时就停止。那么就比较容易写出来了，其中任意一个单趟排序都可以调用。

代码如下：

//前后指针法单趟排序
int PartSort1(int *a,int left,int right)
{
    int keyi = left;//先保存最左侧下标，作为keyi

    while (left < right)
    {
        //先让右走，找小，并且不能越界
        while (left < right && a[right] >= a[keyi])
        {
            --right;
        }

        //再让左走，找大，不越界。
        while (left < right && a[left] <= a[keyi])
        {
            ++left;
        }

        //交换左边大的，和右边小的
        Swap(&a[left], &a[right]);
    }

    //循环完成，我们在最后交换下，相遇位置的和原来keyi位置的值
    Swap(&a[keyi], &a[left]);

    //返回相遇位置的下标是为进行下一步递归。
    return left;
}

//挖坑法
int PartSort2(int* a, int left, int right)
{
    int key = a[left];//保存最左边初始位置的值

    while (left < right)
    {
        while (left < right && a[right] >= key)
        {
            --right;
        }

        a[left] = a[right];//产生一个坑位

        while (left < right && a[left] <= key)
        {
            ++left;
        }

        a[right] = a[left];//上一个坑位填上，产生新的坑位
    }

    a[left] = key;//把最后的坑位填上了。

    return left;//返回最后相遇的下标，以便后序递归
}


//前后指针法
int PartSort3(int *a, int left, int right)
{
    int prev = left;//后指针
    int cur = left + 1;//前指针
    int keyi = left;//初始位置

    while(cur <= right)//当cur小于等于最右边时进入循环
    {
        //当cur找到比初始位置大的数，如果此时cur不等于prev，
        //那么就交换cur和++prev，一定是前置++。
        if (a[cur] < a[keyi] && prev != cur)
        {
            Swap(&a[cur], &a[++prev]);
        }
        cur++;
    }
    Swap(&a[prev], &a[keyi]);//最后交换prev和初始位置即可

    return prev;//返回prev为了后续递归做铺垫
}

void QuickSort(int *a, int begin, int end)
{
    if (begin >= end)//如果 begin >= end表示区间只有一个数，或者没有数
    {
        return;
    }

    //接收第一趟排序的返回值，即是我们下面数据的分割线
    int keyi = PartSort3(a, begin, end);

    //分为左区间和右区间，进行递归
    QuickSort(a, begin, keyi - 1);
    QuickSort(a, keyi + 1, end);

}

非递归版：

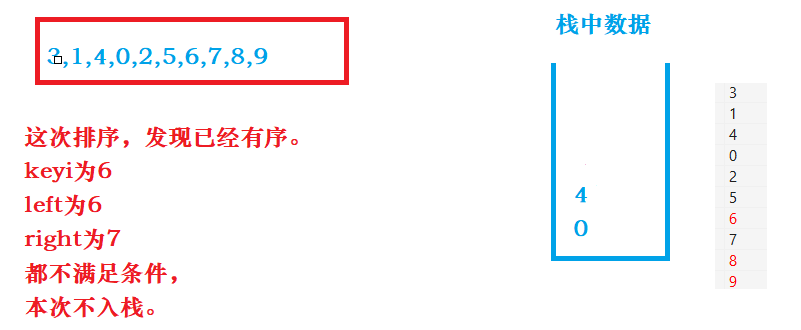
非递归版本我们使用 栈 这个数据结构帮助我们解决，我们利用 栈 后进先出的特性，把下标放入栈中，然后单趟排序，再把单趟排序的两段分别放入栈中，如此反复，我们就可以把数据排序完成。

代码如下：

//非递归版本实现
void QuickSortNonR(int* a, int begin, int end)
{
    ST st;
    StackInit(&st);
    StackPush(&st, begin);//把最开始数据的第一个下标放入栈中
    StackPush(&st, end);//把最开始数据的最后一个下标放入栈中

    while (!StackEmpty(&st))//栈不为空继续
    {
        int left, right;//定义左右下标，用来判断是否要继续排序
        right = StackTop(&st);//出右下标
        StackPop(&st);

        left = StackTop(&st);//出左下标
        StackPop(&st);

        int keyi = PartSort1(a, left, right);//单趟排序
        
        //排序好左边的数据个数大于1个，就继续排序
        if (left < keyi - 1)
        {
            StackPush(&st, left);//把左下标入栈
            StackPush(&st, keyi - 1);//把排序好位置的左边的下标入栈
        }

        //排序好右边的数据个数大于1个，就继续排序
        if (keyi + 1 < right)
        {
            StackPush(&st, keyi + 1);//把排序好位置的右边的下标入栈
            StackPush(&st, right);//右下标入栈
        }
        
    }

    StackDestroy(&st);
}

下面用流程图演示下：

快速排序的时间复杂度分析：

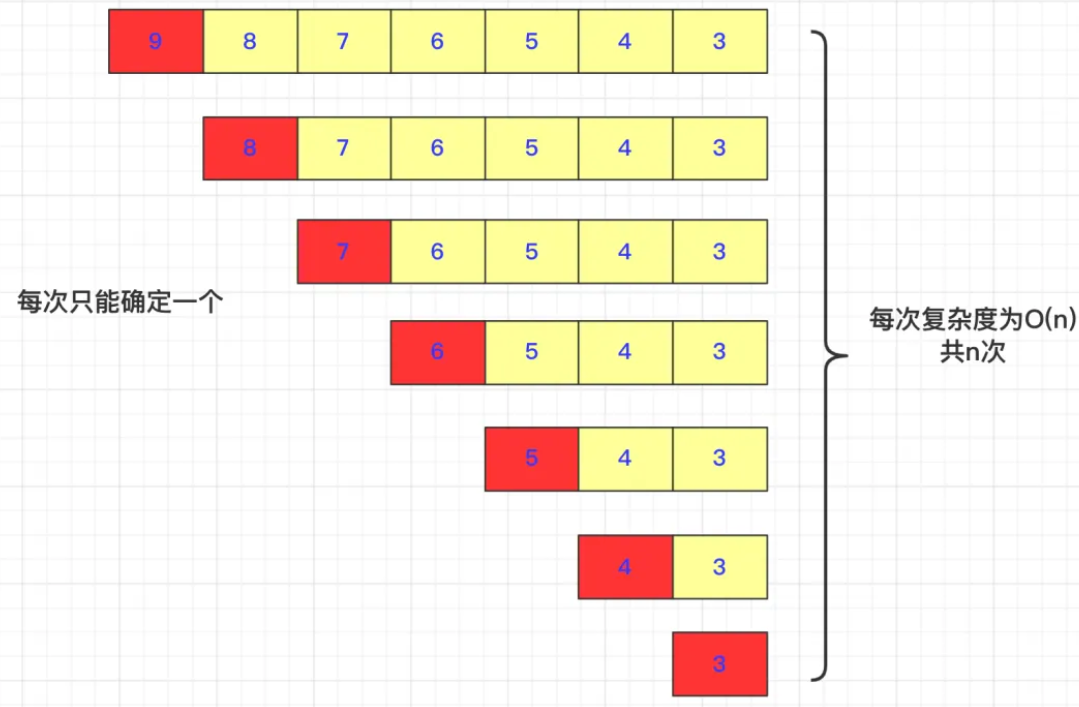
我们先拿最坏的举例（O(N*N)）：

** 快速排序每次确定一个数，每次交换为等差数列，（n，n-1，n-2，...，2,1），一共n个数，所以在最坏的情况下是O(NN）。*

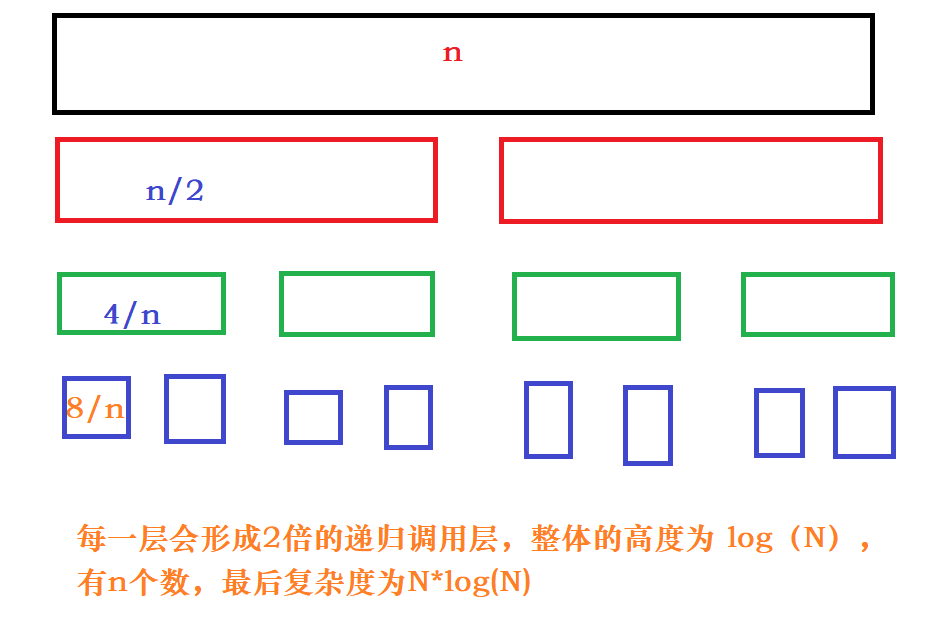
一般情况下复杂度为（ O(N*log(N)) ）：

快速排序的优化：

三数取中：

1.我们要避免最坏的情况出现，所以我们加上一个算法，叫三数取中算法即可，这样的最坏情况下的逆序变成最好情况啦。

代码实现：

int GetMidIndex(int* a, int left, int right)
{
    int mid = (left + right) / 2;

    if (a[left] < a[mid])
    {
        if (a[mid] < a[right])
        {
            return mid;
        }
        else if (a[right] < a[left])
        {
            return left;
        }
        else
        {
            return right;
        }
    }
    else
    {
        if (a[mid] > a[right])
        {
            return mid;
        }
        else if (a[left]<a[right])
        {
            return left;
        }
        else
        {
            return right;
        }
    }

}

减少最后几层递归调用：

** 2.我们可以在递归调用的最后几层使用其他的排序算法，因为最后几层的递归调用太多，消耗的成本太大啦，所以使用插入排序更好点。我们使用插入排序时，注意我们要排序的区间不要整错了。**

//递归版
void QuickSort(int *a, int begin, int end)
{
    if (begin >= end)//如果 begin >= end表示区间只有一个数，或者没有数
    {
        return;
    }

    if (end - begin > 20)
    {
        //接收第一趟排序的返回值，即是我们下面数据的分割线
        int keyi = PartSort3(a, begin, end);

        //分为左区间和右区间，进行递归
        QuickSort(a, begin, keyi - 1);
        QuickSort(a, keyi + 1, end);
    }
    else
    {
        //使用插入排序
        InsertSort(a + begin, end - begin - 1);
    }

}