机械臂要想到达期望的位置，必须将其感知系统和机械臂运动产生联系，这关键的两步就是手眼标定和坐标系转换。按我所讲的步骤进行调试一定可以成功。
1.手眼标定
机械臂手眼标定目的是为了求得三个参数：机械臂末端位姿矩阵、末端与相机的变换矩阵以及相机到标定板的变换矩阵。其中，末端与相机的变换矩阵是求解的关键。机械臂的末端位姿矩阵可通过ROS订阅话题得出，相机到标定板的变换矩阵可通过外参标定得出，末端与相机的变换矩阵可通过AX=XB模型求出。
1.1 相机标定
相机标定是手眼标定的最先应进行的工作，目的是为了获取相机的内外参数，畸变矩阵。相机标定不仅可以用于机械臂手眼标定，还可以用于多个相机间的校准、对齐，实现多模态图像配准。
1.将标定板放置在距离机械臂一定距离处，距离不应太远。值得注意的是，标定板的横向格数一定不能等于纵向格数，否则不同图像中的同一个角点坐标并不对应，如下图为**错误案例**。
2.将realsense相机稳定固定在机械臂末端，打开realsense-viewer，通过施教模式控制机械臂到达某个位置，依次在终端输入下面命令可订阅机械臂的位姿，记录此时的机械臂四元数矩阵和realsense拍摄的画面。
rosrun moveit_commander moveit_commander_cmdline.py
use <group name>
current
3.将四元数转换为机械臂旋转矩阵，如下代码
from scipy.spatial.transform import Rotation as R
Rq=[-0.756325124972, 0.269649470864,-0.54434743131, 0.24279073752] # 四元数
Rm = R.from_quat(Rq)
rotation_matrix = Rm.as_matrix() # 旋转矩阵
print('rotation:\n',rotation_matrix)
4.将旋转矩阵和第2步得到的平移量记录为四行四列的齐次矩阵，并记录旋转矩阵和平移矩阵于RobotToolPose.csv中。
1.2 手眼标定
原理讲解（不想看的可以跳过）：
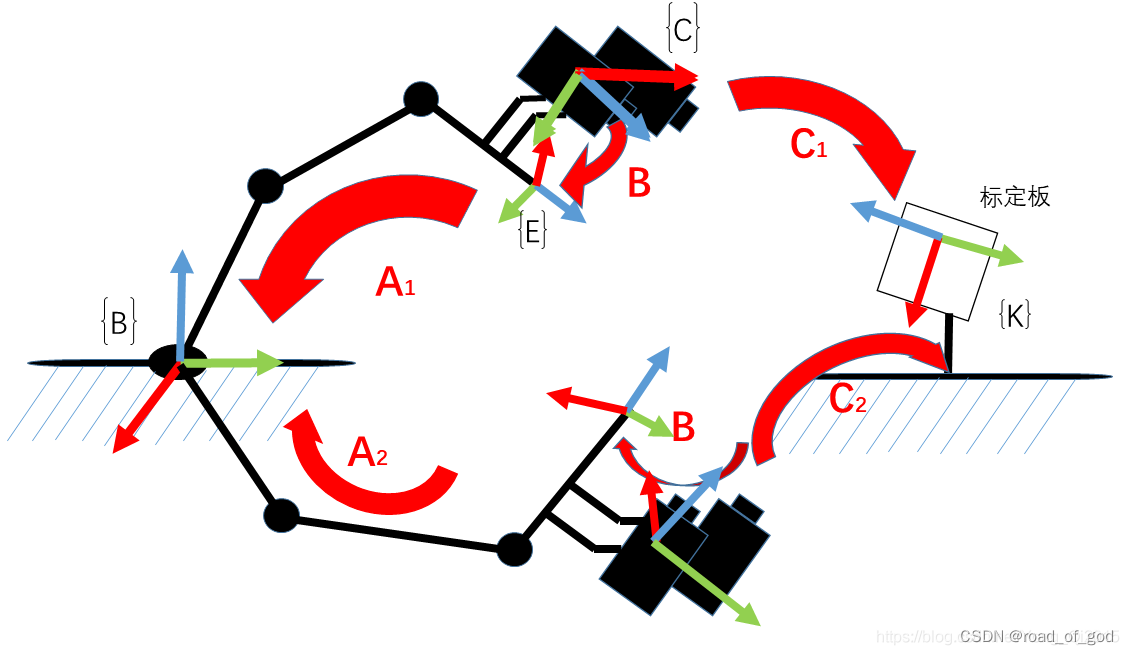
A：机器人末端在机械臂坐标系下的位姿，这其实就是机器人运动学正解的问题。（已知）。
B：相机在机器人末端坐标系下的位姿，这个变换是固定的，只要知道这个变换，我们就可以随时计算相机的实际位置，所以这就是我们想求的东西。（未知，待求）
C：相机在标定板坐标系下的位姿，这个其实就是求解相机的外参（已知）
话不多说，直接上代码
# coding=utf-8
# copied by ysh in 2021/12/08
"""
用于相机标定和相机的手眼标定
A2^{-1}*A1*X=X*B2*B1^{−1}
"""
import os.path
import cv2
import numpy as np
np.set_printoptions(precision=8,suppress=True)
import glob
path = "D:/hand_eye_image/"
# 角点的个数以及棋盘格间距
XX = 8
YY = 6
L = 0.03 # 格子大小
# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 获取标定板角点的位置
objp = np.zeros((XX * YY, 3), np.float32)
objp[:, :2] = np.mgrid[0:XX, 0:YY].T.reshape(-1, 2) # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y
objp = L*objp
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
images = glob.glob('{}/*.png'.format(path))
print(images)
i = 0
for fname in images:
print(fname)
img = cv2.imread(fname)
# cv2.imshow('img',img)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
size = gray.shape[::-1]
ret, corners = cv2.findChessboardCorners(gray, (XX, YY), None)
print(ret)
if ret:
obj_points.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (3, 3), (-1, -1), criteria) # 在原角点的基础上寻找亚像素角点
#print(corners2)
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)
cv2.drawChessboardCorners(img, (XX, YY), corners, ret)
# 红色为第一个点，蓝色为最后一个点，先X轴再Y轴
cv2.imwrite('{}/figure_save/{}.png'.format(path,i), img)
i = i+1
# cv2.imshow('img', img)
# cv2.waitKey(2000)
N = len(img_points)
print(f'图像个数：{N}')
# cv2.destroyAllWindows()
# 标定,得到图案在相机坐标系下的位姿
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
# print("ret:", ret)
print("内参矩阵:\n", mtx) # 内参数矩阵
print("畸变系数:\n", dist) # 畸变系数 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs) # 旋转向量 # 外参数
print("tvecs:\n", tvecs ) # 平移向量 # 外参数
print("-----------------------------------------------------")
# img2 = cv2.imread(f'{path}/figure/*.jpg')
i = 0
for fname in images:
figure = cv2.imread(fname)
h, w = figure.shape[:2]
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),0,(w,h)) # 自由比例参数,用于去除畸变矫正后图像四周黑色的区域。alpha=0，则去除所有黑色区域，alpha=1，则保留所有原始图像像素，其他值则得到介于两者之间的效果。
dst = cv2.undistort(figure, mtx, dist, None, newcameramtx)
cv2.imwrite('{}/figure_undist/{}.png'.format(path,i), dst)
i = i + 1
# 机器人末端在基座标系下的位姿
tool_pose = np.loadtxt('{}/RobotToolPose.csv'.format(path),delimiter=',',encoding='utf-8-sig')
R_tool = []
t_tool = []
for i in range(int(N)):
R_tool.append(tool_pose[0:3,4*i:4*i+3])
t_tool.append(tool_pose[0:3,4*i+3])
R, t = cv2.calibrateHandEye(R_tool, t_tool, rvecs, tvecs, cv2.CALIB_HAND_EYE_TSAI) # R_tool, t_tool手爪相对于机器人基坐标系的旋转矩阵与平移向量；rvecs, tvecs标定板相对于双目相机的齐次矩阵
T_tool_camera = np.hstack((R, t)) # R,T就是相机到机械臂末端的旋转偏移矩阵
T_tool_camera = np.vstack((T_tool_camera, np.array([0,0,0,1])))
print(f'相机在机器人末端坐标系的位姿：\n{T_tool_camera}')
with open('{}/camera.txt'.format(path), 'w') as f:
f.write(f'{mtx}\n') # 内参矩阵
f.write(f'{dist}\n') # 畸变矩阵
f.write(f'{T_tool_camera}') # 相机到机械臂的外参矩阵
需要自己调整的参数有：标定板分别在XX,YY角点数量，标定板单位格的宽（高）L，存储地址path，机器人位姿RobotToolPose.csv。最后可以得到相机内参矩阵mtx，相机到机械臂的外参矩阵T_tool_camera。
附：手眼标定原理讲解http://t.csdn.cn/KoFM9
2. 像素-世界坐标系转换
完成手眼标定后，我们手中就有了相机内参矩阵mtx，相机到机械臂的外参矩阵T_tool_camera。接下来就是最后一步：坐标系转换。
原理讲解(不想看的可以跳过)：
（1）顺序变换
** 世界坐标系-相机坐标系**
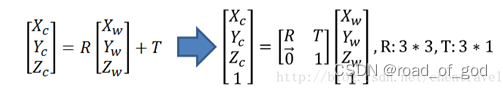（1）
** 相机坐标系-像素坐标系**
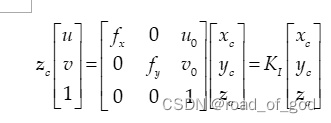 （2）
KI是内参矩阵，xc,yc,zc为相机坐标系坐标，u,v是像素坐标系坐标
** 像素坐标系到世界坐标系**
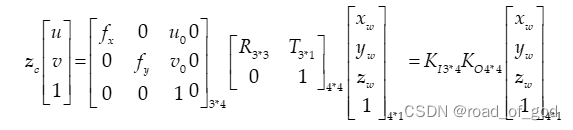（3）
u,v是像素坐标系坐标，xw yw zw是世界坐标系坐标，等式右第一个矩阵是内参矩阵，第二个矩阵是外参矩阵。但是不能直接乘，因为涉及到求得3*4矩阵无法求逆矩阵，所以不能直接用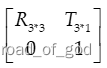，而是要用。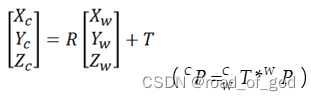
将（1）变形：
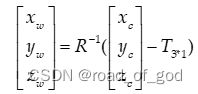 （4）
将（2）带入（4）：
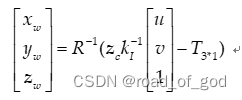
** （2）直接变换**
其中，XwYwZw为世界坐标系坐标，R为外参中的旋转矩阵，KI为内参矩阵，Zc为相机坐标系中的深度值，u，v为像素坐标
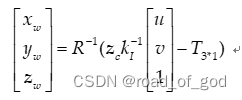
话不多说，直接上代码
import numpy as np
matrixHand2Camera = np.array([[ 0.56186877, -0.82718502, -0.00827197, 0.00665606],
[ 0.82722097,0.56180082, 0.00923615, -0.0420225],
[-0.00299281 , -0.01203225, 0.99992313, 0.02549419],
[ 0, 0, 0, 1 ]]) # 手眼矩阵THC
matrixBase2Hand = np.array([[0.26195007, -0.14356031, 0.95434407, 0.319418241631],
[-0.67221037, -0.73668364, 0.07369148, -0.010993728332],
[0.69247049, -0.66082346, -0.28947706, 0.689715275419],
[0, 0, 0, 1 ]]) # 末端姿态TBH
matrixCamera2Pixel = np.array([[922.78685321, 0, 657.06183115],
[ 0, 923.92329954, 366.06665478],
[ 0, 0, 1 ]]) # 内参
matrixBase2Camera = np.dot(matrixBase2Hand,matrixHand2Camera)
matrixCamera2Base = np.linalg.inv(matrixBase2Camera)
zc = 0.495
u = 801
v = 452
# 直接变换
outputBase2 = np.dot(np.linalg.inv(matrixCamera2Base[0:3,0:3]),zc*np.dot(np.linalg.inv(matrixCamera2Pixel),np.array([u,v,1]).reshape(3,1))-matrixCamera2Base[:3,3].reshape(3,1))
print("直接变换",outputBase2)
** 根据上述代码，即可求得像素坐标系一点在机械臂基坐标系下的位置，到此就完成了视觉系统感知+机械臂运动一体化流程。**
** 值得注意的是，**matrixBase2Camera要先求逆才可带入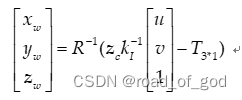
中，因为公式中的R和T实际为基坐标相对于相机的位置
，而matrixBase2Camera为相机相对于基坐标位姿
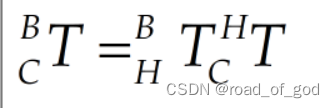，根据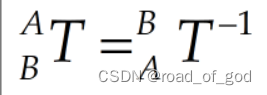
，求得基坐标相对于相机的位置matrixCamera2Base。
附：坐标系转换http://t.csdn.cn/r4Pwq
本文转载自: https://blog.csdn.net/road_of_god/article/details/126891153
版权归原作者 road_of_god 所有， 如有侵权，请联系我们删除。
版权归原作者 road_of_god 所有， 如有侵权，请联系我们删除。