꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客系列专栏:机器学习系列专栏
"探索未来,掌握人工智能"🚀 点击加入我们的AI学习之旅,让技术变得有趣又易懂,点击跳转
**我的目标:"团团等我💪( ◡̀_◡́ ҂)" **( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!

一.AI序列决策问题
AI序列决策问题是指在人工智能领域中,智能体需要在一个序列的环境中做出一系列决策,以达到某个目标或最大化某种累积奖励的问题。这类问题通常涉及到强化学习,其中智能体通过与环境的交互来学习最优的行为策略。
1.序列决策问题的特点:
- 时间维度:决策不是一次性的,而是需要在一系列时间步骤中进行。每个决策都会影响后续的状态和可能的决策。
- 状态变化:智能体的每个决策都会使环境从一个状态转移到另一个状态。状态可以是环境的描述,如游戏的当前分数、机器人的位置等。
- 奖励反馈:智能体在每个时间步骤做出决策后,环境会提供一个奖励(或惩罚),这是对智能体决策好坏的反馈。
- 长期目标:智能体的目标通常是长期的,比如最大化累积奖励、达到最终的胜利状态或完成任务。
- 不确定性:智能体在做出决策时可能无法完全了解环境的全部特性,因此需要在不确定性中做出最优的选择。
2.解决序列决策问题的AI方法:
- 强化学习:通过智能体与环境的交互来学习最优策略。智能体通过尝试不同的行动并接收环境的奖励或惩罚来学习。
- 动态规划:一种基于模型的优化方法,通过预测未来的状态和奖励来计算当前行动的价值。
- 蒙特卡洛方法:通过随机模拟来估计行动的价值,适用于难以精确建模的环境。
- 时序差分学习:结合了动态规划和蒙特卡洛方法的特点,通过学习状态和行动之间的差异来更新价值估计。
- 深度学习:使用深度神经网络来近似复杂的价值函数或策略函数,尤其在状态空间高维且连续时表现出色。
3.序列决策问题的应用场景:
- 游戏AI:如棋类游戏、电子游戏等,智能体需要通过一系列行动来赢得比赛。
- 机器人控制:机器人需要根据环境的变化做出连续的移动和操作决策。
- 自动驾驶汽车:汽车需要根据路况和交通规则做出连续的驾驶决策。
- 资源管理:如电网管理、网络带宽分配等,需要根据实时数据做出一系列调度决策。
AI序列决策问题是人工智能中一个非常重要且活跃的研究领域,它不仅挑战着智能体在复杂环境中的学习能力,也推动了AI技术在多个领域的应用和发展。
二.Q-Learning算法通过学习最优策略
Q-Learning算法是一种强化学习方法,它专注于学习一个名为Q函数的值表,该值表估计了在给定状态下采取特定行动所能获得的长期回报。Q-Learning的目标是找到一个最优策略,即在每个状态下选择能够最大化长期回报的行动。这个过程可以分为以下几个关键步骤:
1. 初始化
在开始学习之前,Q函数的初始值通常被设置为零。这意味着在没有任何经验的情况下,对于任何给定的状态和行动组合,其预期的长期回报都被假定为零。
2. 探索与利用
智能体在环境中执行行动时,需要在探索新行动和利用已知最优行动之间做出权衡。探索是指尝试新的行动以发现更有价值的策略;利用是指基于当前知识选择最佳的已知行动。Q学习算法通常使用ε-greedy策略或其他方法来平衡探索和利用。
3. 更新规则
Q-Learning 的核心是其更新规则,Q-Learning的迭代公式是著名的贝尔曼方程:,该规则根据以下公式来更新Q值:

上式左端的Q(s,a)是状态s下动作a的新Q值;右边的Q(s,a)是原来的Q值;R是执行动作a后得到的奖励;maxQ(s,a,)是下一状态 S', 下,所有的动作 a', 中最大的Q值;参数0≤α≤1,0≤ϒ≤1。
常用其简化形式,取 α=1,方程为

- Q(s,a) 是当前状态-行动对的Q值。
- α 是学习率,控制新信息覆盖旧信息的速度。
- R 是收到的即时奖励。
- γ 是折扣因子,它决定了未来奖励的当前价值。
- 's′ 是行动后的新状态。
- maxα′Q(s′,a′) 是新状态下所有可能行动的最大Q值。
这个更新规则的目的是根据即时奖励和新状态下的最佳预期回报来调整当前状态-行动对的Q值。
Q值更新方法:
随机选一个初始状态 s;
看当前状态 s 可以转到哪?随机选一个 s',得到奖励 R;
再看新状态 s',可以转到哪?求出这些状态的最大的Q值(状态没变,还是 s',)
代入公式计算,并更新 Q(s,a),此时当前位置变成了s'。
如果s',已是目标状态,则本片段迭代结束;否则从s',开始,重复上面操作,直至s',到达目标状态,即完成了一个迭代片段。如下图。

这里奖励矩阵的作用是,查看各个状态可以直接转移到其它哪些状态。Q值矩阵表示的是,各个状态及动作的Q值。
4. 收敛与最优策略
随着智能体不断地与环境交互并更新Q值,Q函数会逐渐收敛到最优Q函数。最优Q函数提供了在每个状态下采取哪个行动可以最大化长期回报的确切信息。一旦Q函数收敛,智能体可以简单地选择具有最高Q值的行动来执行,这样的策略被称为贪婪策略,它对应于最优策略。
5. 离线与在线学习
Q-Learning可以在线进行,即智能体在实际探索环境的同时更新Q值;也可以离线进行,即智能体从一个已经收集的经验数据集(称为回放缓冲区)中学习。离线学习有助于打破数据之间的时间相关性,提高学习的稳定性。
6. 应用
Q-Learning算法已经被成功应用于多种领域,包括游戏、机器人控制、资源管理等。它能够处理离散状态和行动空间的问题,并且在某些情况下,它能够学习到非常复杂的策略。
总结来说,在实际应用中,一旦智能体学习到了最优策略,它就可以在环境中执行该策略来完成任务或游戏。例如,在游戏AI中,智能体可以使用最优策略来赢得比赛;在机器人控制中,智能体可以使用最优策略来高效地导航和执行任务。Q-Learning能够解决AI中的序列决策问题,使智能体能够在复杂的环境中做出最优的决策。这种方法不需要预先知道环境的全部动态,也不需要大量的标记数据,因此它非常适合于那些难以直接建模的复杂问题。
三.通过经典的“冰湖”问题来解析Q-Learning算法

“冰湖”问题是一个格子世界,智能体(通常表示为小人)从起点开始,目标是到达终点(通常标记为G)。在这个过程中,小人需要避开冰洞(标记为H),并且必须面对不可控的滑动。每次小人尝试移动时,有1/3的概率会滑动到相邻的非目标格子,这增加了问题的难度。
环境设置
- 状态(State):每个格子代表一个状态。
- 行动(Action):智能体可以选择向上、向下、向左或向右移动。
- 奖励(Reward):除了到达目标位置获得正奖励外,每次移动通常没有奖励。掉入冰洞会得到负奖励。
- 折扣因子(Gamma):用于计算未来奖励的当前价值。
**Q表初始化 **
Q表是一个二维数组,其行数等于状态数量,列数等于行动数量。所有Q值最初被初始化为零,表示智能体对环境一无所知。
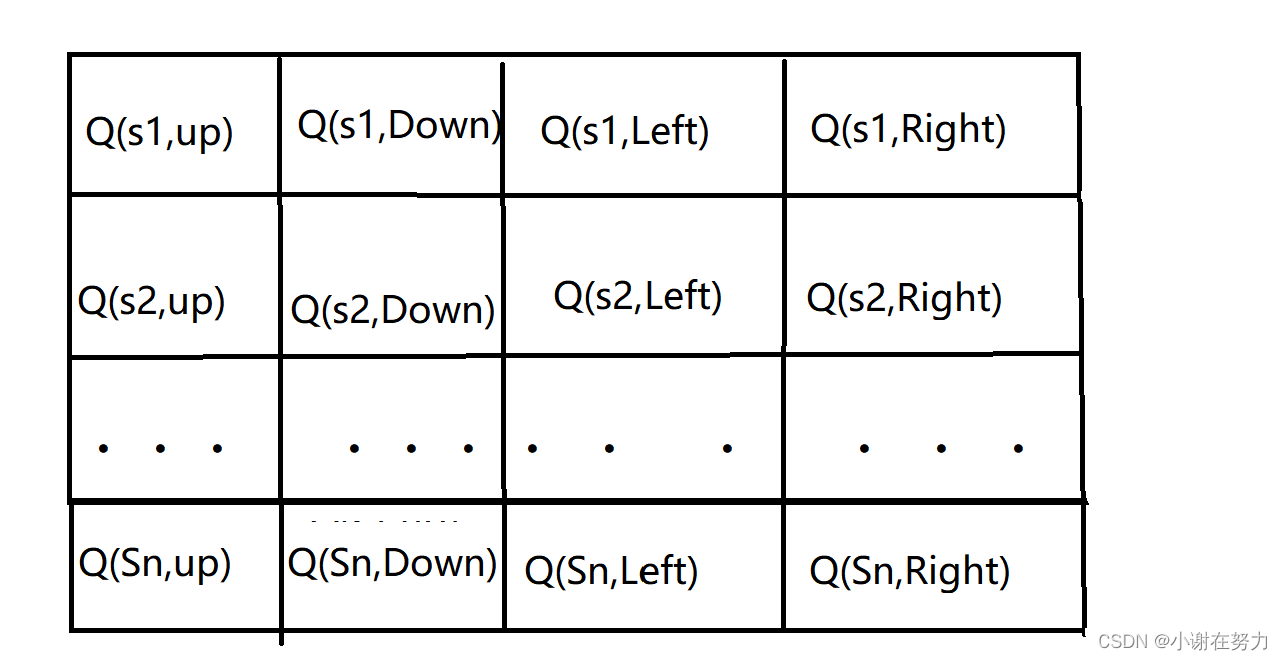
**在这个图示中,
s1
到
sn
表示不同的状态,每个状态对应四个可能的行动(上、下、左、右)。每个单元格的值初始化为零。随着智能体与环境的交互,这些值将根据Q学习算法的更新规则逐渐改变,以反映在特定状态下采取特定行动的预期累积奖励。 **
注意:
这个图示是一个简化的版本,实际的Q表可能会更大,并且状态和行动的数量将根据具体的问题环境而定。此外,实际的Q表可能不会以这种二维表格的形式直观展示,而是作为一个多维数组在计算机程序中进行管理和更新。
**算法流程 **
- 导入必要的库并创建环境。
- 初始化Q表和其他超参数,如学习率(Learning Rate)、折扣因子(Gamma)、探索率(Epsilon)等。
- 对于每一回合(Episode)的训练: - 重置环境并获取初始状态。- 在状态下选择行动,可以是随机选择(探索)或基于当前Q表选择最大Q值的行动(利用)。- 执行行动并观察新状态和奖励。- 如果达到终止条件(如掉入冰洞或到达目标),则结束该回合。- 更新Q表: ** Q(s,a)←Q(s,a)+α[r+γmaxα′Q(s′,a′)−Q(s,a)]**- 根据需要调整探索率(Epsilon)。- 随着训练的进行,逐渐减少探索率,以便智能体更多地利用已学到的知识。- 训练完成后,使用训练好的Q表来指导智能体行动。
简化版Python代码
这个例子使用了gym库,它是一个常用的强化学习环境集合
import numpy as np
import gym
# 初始化环境
env = gym.make('FrozenLake-v1')
env.seed(0)
# 初始化Q表
action_space_size = env.action_space.n
state_space_size = env.observation_space.n
Q = np.zeros((state_space_size, action_space_size))
# 设置超参数
learning_rate = 0.8
discount_factor = 0.95
num_episodes = 5000
epsilon = 1.0 # 初始探索率
min_epsilon = 0.01 # 最小探索率
decay_rate = 0.005 # 探索率衰减率
for episode in range(num_episodes):
state = env.reset()
total_reward = 0
done = False
while not done:
# 选择行动
if np.random.rand() < epsilon:
action = env.action_space.sample()
else:
action = np.argmax(Q[state, :])
# 执行行动并获取新状态和奖励
new_state, reward, done, _ = env.step(action)
total_reward += reward
# 更新Q表
if done:
next_state = None
max_future_Q = 0
else:
next_state = new_state
max_future_Q = np.max(Q[next_state, :])
old_Q = Q[state, action]
Q[state, action] = (1 - learning_rate) * old_Q + learning_rate * (reward + discount_factor * max_future_Q)
state = new_state
epsilon = min_epsilon + (epsilon - min_epsilon) * np.exp(-decay_rate * episode)
print(f'Episode {episode}: Total reward = {total_reward}')
# 完成训练后,使用Q表来玩冰湖游戏
env.reset()
state = env.reset()
done = False
while not done:
action = np.argmax(Q[state, :])
env.step(action)
state = env.unwrapped.observation # 获取下一状态
env.render() # 可视化环境
注意:这只是一个简化的例子,实际的强化学习算法实现可能会更加复杂,并且需要对特定问题进行调整。此外,为了达到更好的性能,可能需要调整超参数、使用更复杂的函数近似方法(如深度学习模型),或者采用其他高级技术。在实际应用中,还需要对算法进行调优和测试,以确保其在特定任务上的有效性和稳定性。
** 感谢你的阅读,祝你一天愉快!**

版权归原作者 小谢在努力 所有, 如有侵权,请联系我们删除。