[ 数据结构 -- 手撕排序算法第二篇 ] 冒泡排序

手撕排序算法系列之：冒泡排序。

从本篇文章开始，我会介绍并分析常见的几种排序，大致包括插入排序，冒泡排序，希尔排序，选择排序，堆排序，快速排序，归并排序等。

大家可以点击此链接阅读其他排序算法：排序算法_大合集（data-structure_Sort）

本篇主要来手撕冒泡排序~~

1.常见的排序算法

1.1交换排序

冒泡排序属于一种交换排序，因此我们在了解冒泡排序之前，先了解一下交换排序的基本思想。

基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置。

交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

2.冒泡排序的实现

2.1基本思想

直接插入排序是一种简单的交换排序法，其基本思想是：

用两个变量指定2个数，如果前一个数比后一个数字大就交换（升序）。

2.2单趟冒泡排序

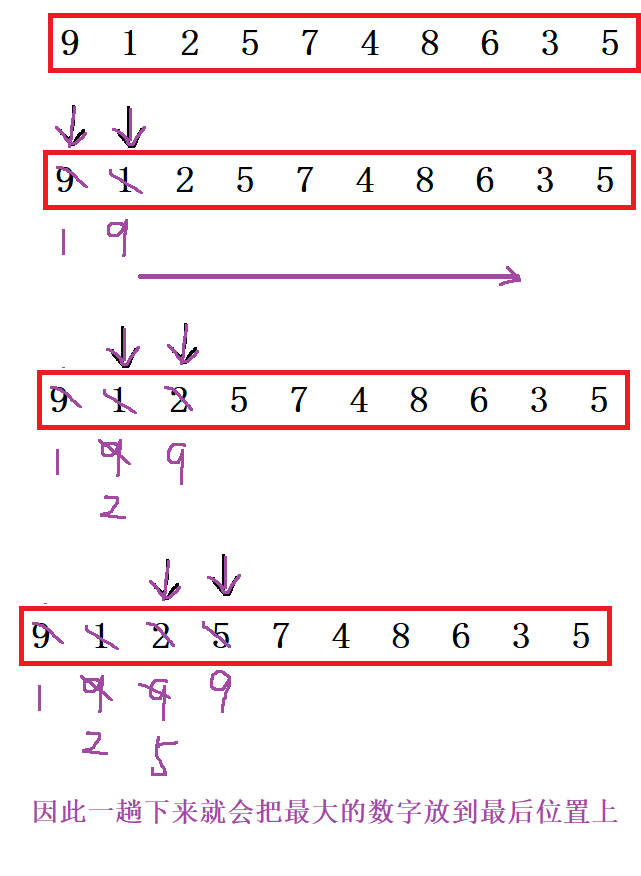
2.2.1思路分析

单趟下来冒泡排序就会把最大的数字放在最后一位（升序）。

2.2.2单趟代码实现

void Swap(int* pa, int* pb)
{
    int tmp = *pa;
    *pa = *pb;
    *pb = tmp;
}
//单趟
for (int i = 1; i < n ; ++i)
{
    if (a[i - 1] > a[i])
        {
        Swap(&a[i - 1], &a[i]);
        }
}

3.冒泡排序代码实现

在单趟的基础之上，加上一个循环，将单趟套进去即可。需要注意的是，每次循环冒出一个数字，因此单趟循环之后到下一次循环中比较次数就要减一，这里我们使用变量来控制即可

void BubbleSort(int* a, int n)
{
    for (int j = 0; j < n; ++j)
    {
        //单趟
        for (int i = 1; i < n - j; ++i)
        {
            if (a[i - 1] > a[i])
            {
                Swap(&a[i - 1], &a[i]);
            }
        }
    }
}

4.冒泡排序测试

void Swap(int* pa, int* pb)
{
    int tmp = *pa;
    *pa = *pb;
    *pb = tmp;
}
//冒泡排序 时间复杂度：O(N^2)
void BubbleSort(int* a, int n)
{
    for (int j = 0; j < n; ++j)
    {
        //单趟
        for (int i = 1; i < n - j; ++i)
        {
            if (a[i - 1] > a[i])
            {
                Swap(&a[i - 1], &a[i]);
            }
        }
    }
}
int main()
{
    //冒泡排序
    TestBubbleSort();
    return 0;
}

测试结果：

5.冒泡排序的时间复杂度

5.1最坏情况

最坏情况：逆序排顺序。假设有n个数，等差数列1+2+3+4+...+n

因此最坏的时间复杂度为O(n^2)。

5.2最好情况

最好情况：有序排有序。对于冒泡排序来说，即使是有序仍然会把每个数进行冒泡。虽然有序，但是冒泡排序不知道呀，仍然按着老套路一个一个比较冒。

因此最好的时间复杂度仍为O(n^2)。

6.冒泡排序的优化写法

在时间复杂度分析的过程中，我们可以发现，如果序列已经有序了，时间复杂度仍然是O(n^2).因此我们可以对这种情况进行优化。

6.1优化思想

我们定义一个变量，在冒泡的过程中，如果有两个数字进行交换，说明原序列不是有序的，但是如果冒一遍发现，没有数字记性交换，说明该序列是有序的，就没必要继续冒下去了。因此，我们可以定义一个exchange变量，其实赋值为0，如果冒一遍有交换，就让exchange = 1，如果没有交换，不改变exchange的值，我们最后只需要判断exchange的值即可的值序列是否有序。

6.2优化代码

void Swap(int* pa, int* pb)
{
    int tmp = *pa;
    *pa = *pb;
    *pb = tmp;
}

//冒泡排序 时间复杂度：O(N^2)
//优化：如果前几个已经有序,比较一遍之后后续的无序再进行比较 直接往后走
//实现:定义一个exchange变量，初始化为0;如果交换就说明变化，将exchange变1.
//没变的话就说明有序，就不用往下走 直接break;

void BubbleSort(int* a, int n)
{
    for (int j = 0; j < n; ++j)
    {
        int exchange = 0;
        //单趟
        for (int i = 1; i < n - j; ++i)
        {
            if (a[i - 1] > a[i])
            {
                exchange = 1;
                Swap(&a[i - 1], &a[i]);
            }
        }

        if (exchange == 0)
            break;
    }
}

int main()
{
    //冒泡排序
    TestBubbleSort();
    return 0;
}

6.3优化算法的时间复杂度

6.3.1 最坏情况

最坏情况仍是逆序排顺序 时间复杂度O(n^2)

6.3.2 最好情况

最好情况是本身就有序，我们在第一遍冒泡过程过，exchange没有改变，我们就break了。

因此此时的时间复杂度是O(n)。

7.冒泡排序的特性总结

冒泡排序的特性总结：

1. 冒泡排序是一种非常容易理解的排序

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：稳定

（本篇完）