坐标变换详解
坐标变换的作用
在一个机器人系统中,每个测量元件测量同一物体得出的信息是不一样的,原因就在于“每个测量元件所测量的数据是基于不同坐标系所测量的”,例如:
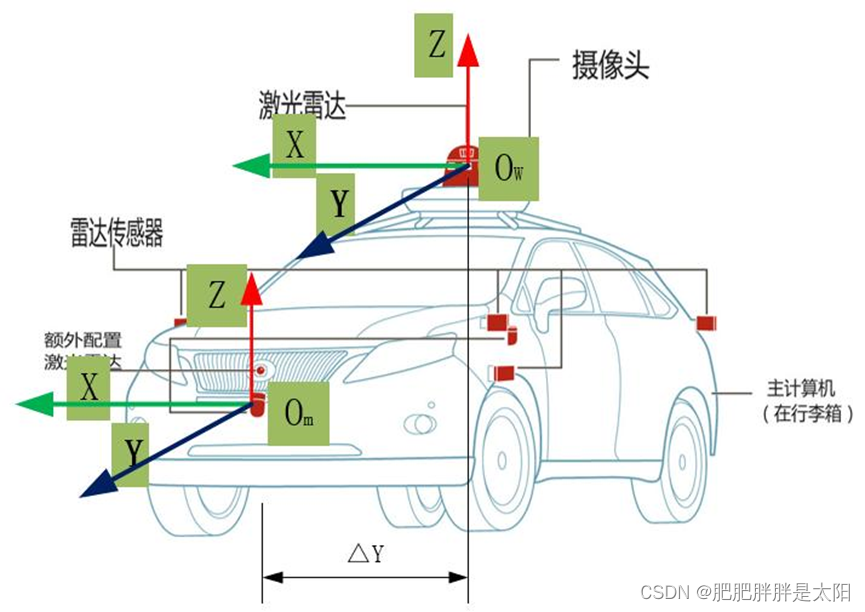
在这辆车中有激光雷达M和激光雷达W,这两个雷达测量的数据截然不同,但是这辆汽车相对于测量物体的位置是唯一的,这就说明“由不同位置雷达测量的数据代表的物理含义(即都表示汽车与被测物体的相对位置)是相同的”。那既然被测物体在不同坐标系中的坐标不同但物理含义相同,这就涉及到不同坐标系中坐标的相互转化。
实现坐标变换所需的数据
我们常用出发与坐标系原点终止于坐标系中坐标点的向量来表示坐标系中坐标点相对于坐标原点的位置(距离+方位)。坐标系的相互转化必须以地球坐标系为媒介才可以实现,即坐标系的相互转化必须已知“任意坐标系中各个坐标轴在world坐标系中的坐标”:
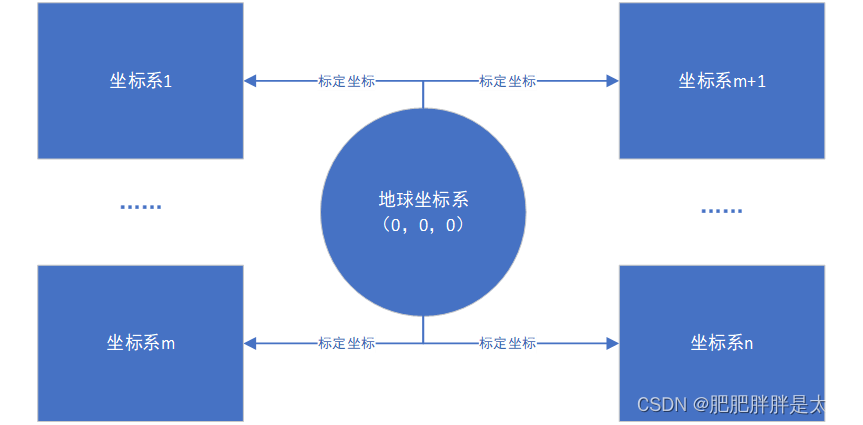
我们会疑惑:world坐标系是什么?
在空间中会有n+1个坐标系,其中只有一个坐标系起到标定作用,也就是说“其他n个坐标系全都是基于该坐标系找到自己在空间中的位置的”。只有大家都知道了自己在空间中的具体位置,坐标转换才可以顺利进行下去。
位姿
基于O1的世界坐标系与基于O2的坐标系如下所示:
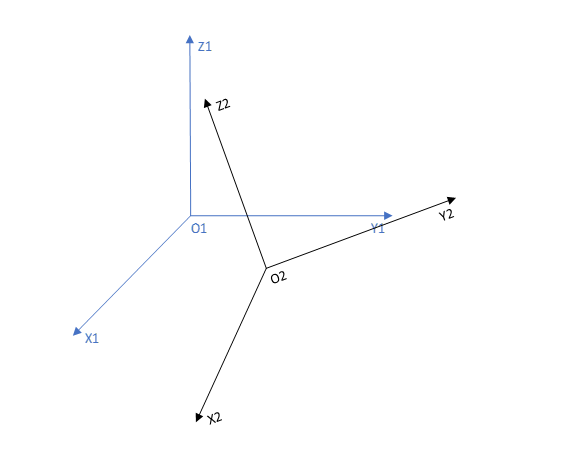
在描述机器人运动时,我们常常提及“位姿”,其实位姿是一个合成词,我们可以将其拆解为“位置+姿态”。位置就是指“机器人某个运动关节/测量传感器在世界坐标系中的具体位置,姿态就是”基于该点的坐标系相较于世界坐标系所进行的旋转“,如下所示:
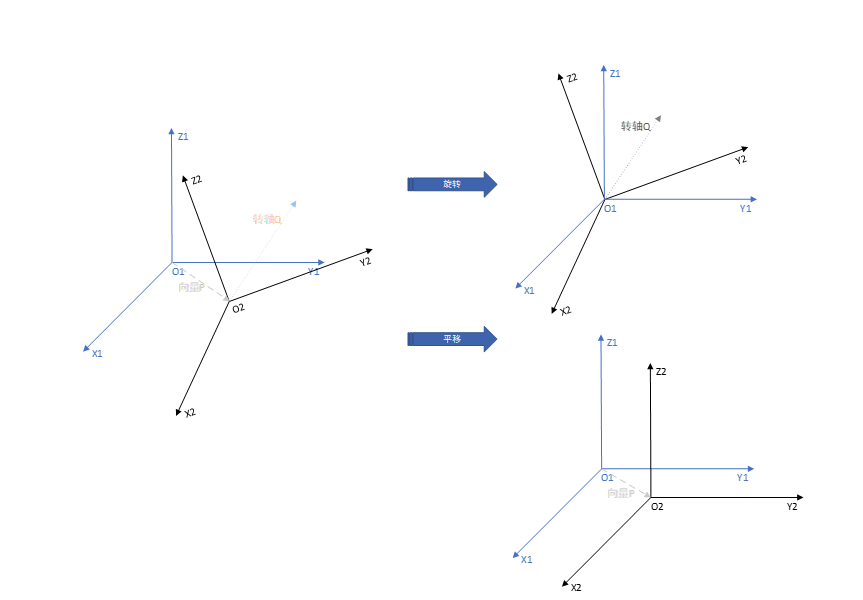
坐标变换中旋转的实质
坐标变换的实质就是“投影”。首先,我们解读一下向量是如何转化为坐标的:
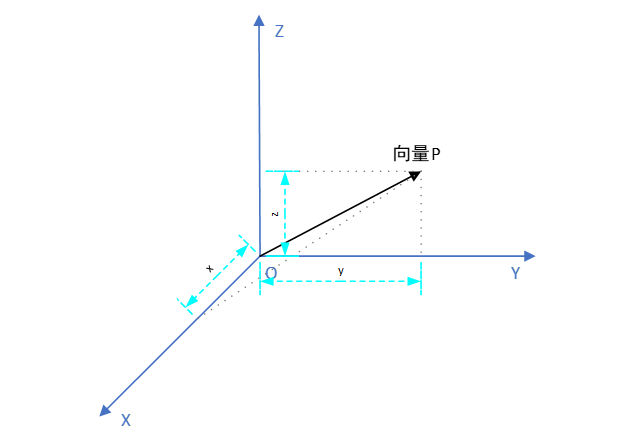
理解向量坐标的由来对于理解坐标变换的实质至关重要!接下来我们考虑一下单位向量在坐标系中的投影:
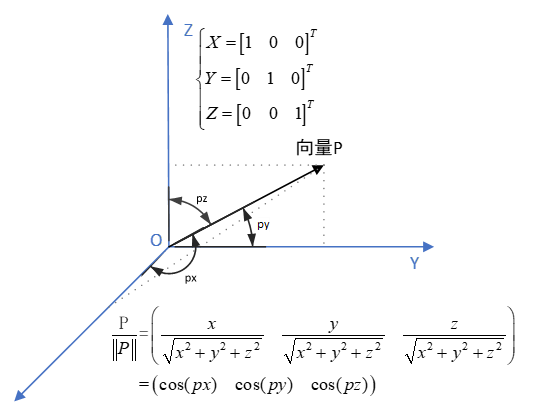
单位向量在坐标系中的投影正好为向量P与各个坐标轴夹角的余弦值。
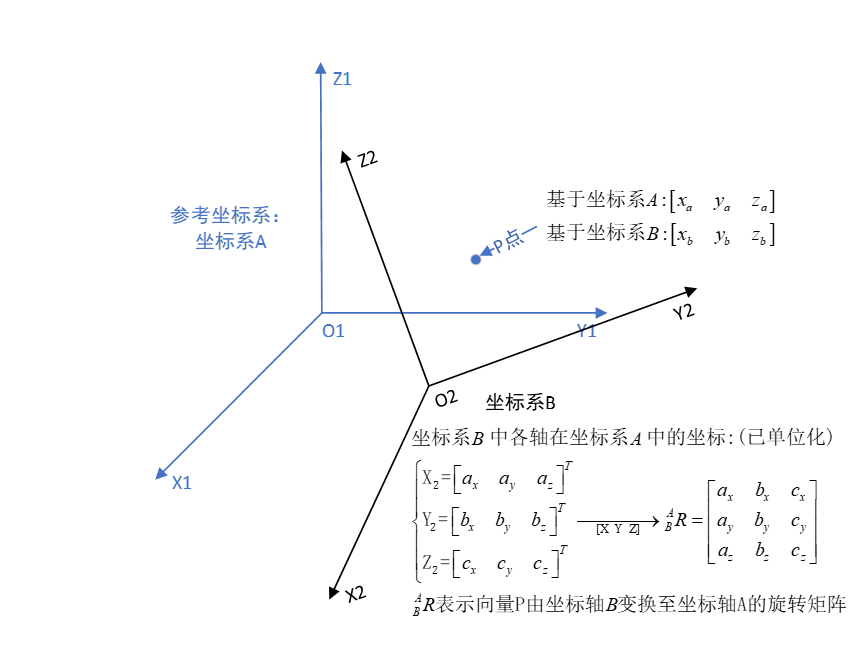
我们将坐标系A作为参考坐标系(world坐标系),基于坐标系A表示坐标系B的各个坐标轴并且将各个向量单位化,由此我们得到一个旋转矩阵,旋转矩阵各个元素的含义如下:

我们先前提到过,向量坐标的计算无非就是投影,那么向量坐标从坐标系B转换至坐标系A无非就是两次投影而已:
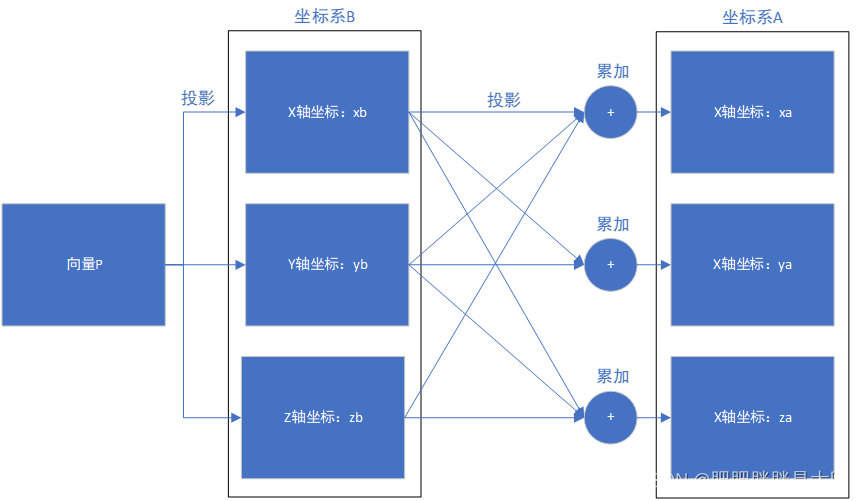
坐标转换的实际意义无非就是将向量P在坐标系A中各个轴的投影分别累加起来形成一个新的坐标。那问题来了,累加如何操作呢?这就涉及旋转矩阵以及矩阵乘法运算了。

其实,这个矩阵的乘法与卷积有着异曲同工之妙。旋转矩阵的性质:
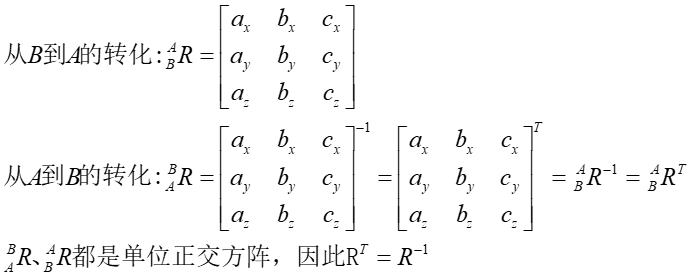
坐标变换中平移的实质
向量可以在坐标系中任意移动,只要不改变向量的方向和大小,向量的属性不会发生变化。但是我们研究的是坐标系B中一个坐标点在坐标系A中的映射,因此需要考虑坐标系B的原点O2相较于坐标系A原点O1平移的距离。
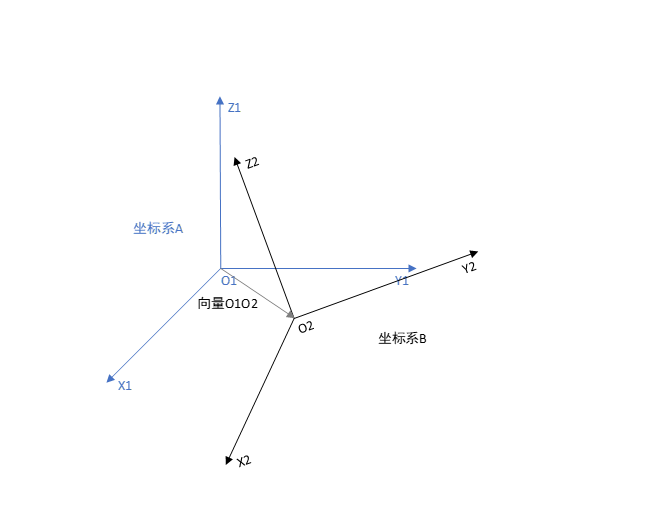
每个基于坐标系B的向量先进性旋转变换,再与向量O1O2求和即可得到向量P再坐标系A中的实际映射。
如何计算坐标系B各坐标轴在坐标系A上的投影?(多坐标变换)
首先,我们要知道世界坐标系下坐标系A/坐标系B的各个坐标轴在世界坐标系(参考坐标系)的坐标:
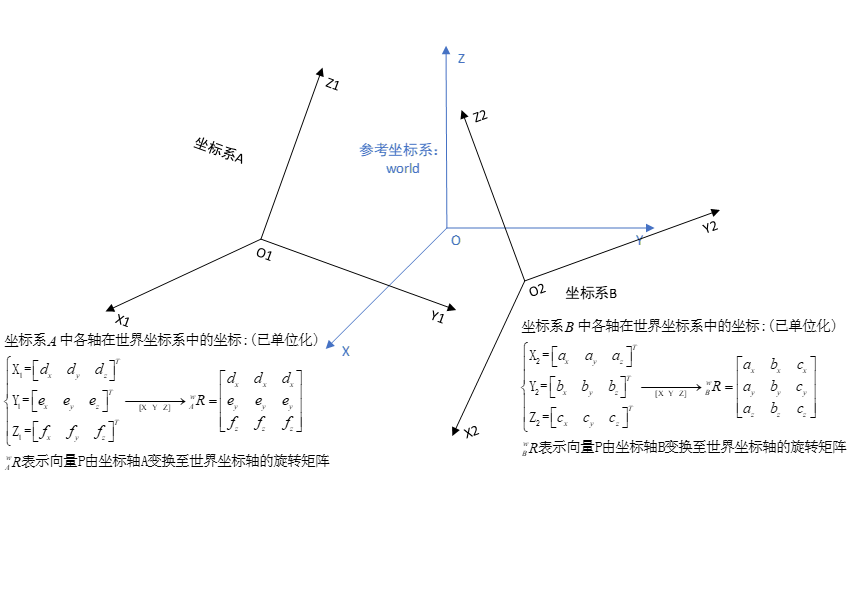
我们使用旋转矩阵的性质可以得到坐标系B变换至坐标系A的旋转矩阵:
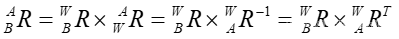
坐标变换流程如下:
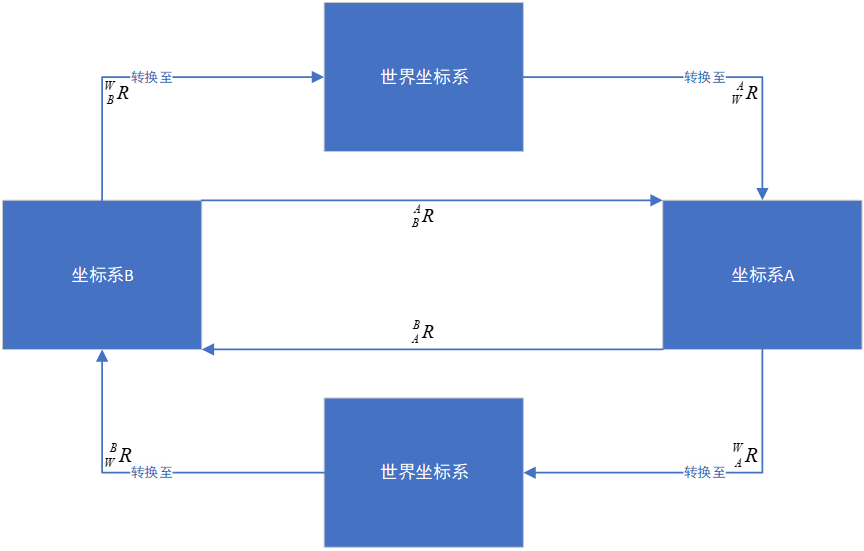
如何实现坐标变换?
我们将P点在坐标系B中的坐标转化为P点在坐标系A中对应的坐标:
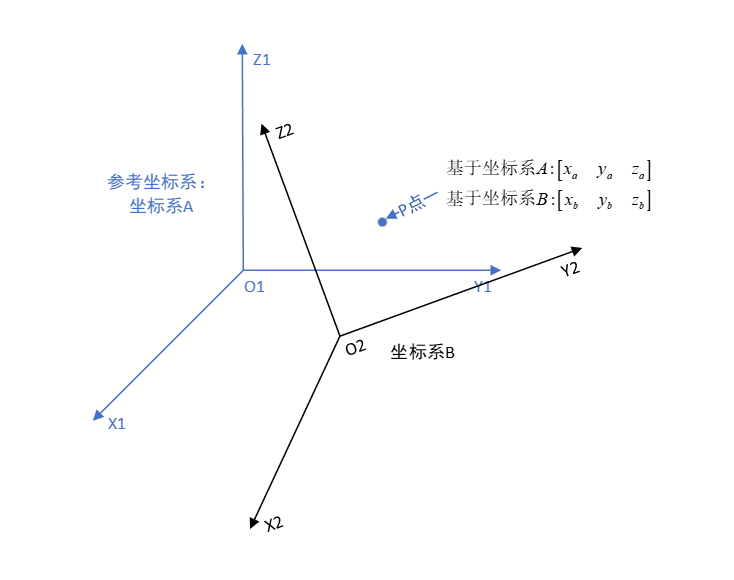
坐标变换=旋转+平移,因此坐标变换表达式如下所示:
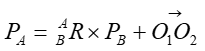
这样不利于矩阵运算,我们可以改写为如下形式:

其中O1O2是从O1指向O2的向量。
版权归原作者 肥肥胖胖是太阳 所有, 如有侵权,请联系我们删除。