
“Men pass away, but their deeds abide.”
人终有一死,但是他们的业绩将永存。
——奥古斯坦-路易·柯西
前言
在学习和训练过程中,需要根据训练样本来确定一组与分类器模型相关的参数。学习过程往往要首先定义某个准则函数,用以描述参数的“合适性”,然后寻找一组“合适性”最大的参数作为学习的结果,也就是将学习问题转化成针对某个准则函数的优化问题
简单函数求极值
对于简单函数,根据数学分析的知识可知:
维矢量
是
的极值点的必要条件是:
- 将所有的偏导数写成矢量形式:
- 函数
的极值点可以通过求解该矢量方程得到
**但是,上述方程的解可能是极大值点,也可能是极小值点,也可能不是极值点,具体情况还需二阶导数来判断。 **
** **如果希望求 的极大值或极小值点,可以通过比较所有的极大值或极小值得到。
复杂函数梯度法求极值
对于简单的纯凸函数或纯凹函数,由于只存在唯一的极值点,极值点即为最大值或最小值点,因此可以直接求解矢量方程  得到 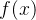 的优化解。
对于复杂函数来说,直接求解矢量方程得到优化函数的极值点往往非常困难。在这种情况下,可以考虑采用迭代的方法从某个初始值开始,逐渐逼近极值点,即——梯度法
泰勒展开
- 如果给定了点
具有所有的前
阶导数的函数
,我们称多项式:
为函数
在点
处的
阶泰勒展开式
泰勒公式是高等数学中的一个非常重要的内容,它将一些复杂的函数逼近近似地表示为简单的多项式函数,泰勒公式这种化繁为简的功能,使得它成为分析和研究许多数学问题的有力工具
考虑到多元函数 在点
附近的一阶泰勒展开式:
其中:
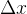 为矢量增量
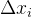 为其第 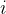 维元素
 为展开式的余项
梯度,Nabla算子
接下来引入梯度的概念
设二元函数
在平面区域
上具有一阶连续偏导数,则对于每一个点
都可以定出一个向量:
称作函数
在点
的梯度,记作
其中:
称为(二维的)向量微分算子或Nabla算子
设
是方向
上的单位向量,则:
当
与梯度方向一致时,有:
此时方向导数
有最大值,值为梯度的模:
我们将其推广到无穷维的情况:
设
维函数
在空间区域
内具有一阶连续偏导数,点
,称向量:
为函数 在点
处的导数,记为
** 稍微集中一下注意力:**
注意到一阶展开式中求和项 ,改写为:
不难发现,该求和式实际上为 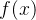 关于  的梯度矢量与矢量增量 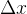 之间的内积。
同时,令 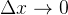,有 ,于是有:
如果要求取 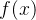 的极小值 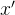,可以从某个初始点 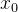 开始搜索,每次增加一个增量 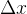,虽然不能保证  直接达到极小值点,但如果能够保证每次迭代过程中函数值逐渐减小:
**那么经过一定的迭代次数之后,函数值能够逐渐逼近极小值 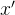,这是一个逐渐下降的过程,因此称为梯度下降法。**
** 更进一步,如果希望下降过程越快越好,用尽可能少的迭代次数逼近极小值,达到对极小值更高精度的逼近,这种方法称为最速下降法**
Cauchy-Schwarz不等式
要使函数值下降的最快,就是要寻找一个矢量增量 使得
最小。
我们引入Cauchy-Schwarz不等式:
其向量形式(欧式空间):
这里不做严谨的证明,且该结论对于大部分人来说非常显然
由于上面我们只展开到一阶近似,当  过大时,余项  便不能忽略,近似的精度会很差。因此不能直接寻找矢量增量,而是应该寻找使得函数值下降的最快的方向,也就是在约束  的条件下,寻找使得 ![[\triangledown f(x)]^T\Delta x](https://latex.csdn.net/eq?%5B%5Ctriangledown%20f%28x%29%5D%5ET%5CDelta%20x) 最小的矢量增量。找到最速下降的方向后,在确定该方向上合适的矢量长度
根据柯西不等式:
令
有:
可以得到,当 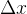 为负的梯度方向时,不等式等号成立,![[\triangledown f(x)]^T\Delta x](https://latex.csdn.net/eq?%5B%5Ctriangledown%20f%28x%29%5D%5ET%5CDelta%20x) 取得最小值,函数值下降速度最快。
所以,最速下降法按照以下方式进行迭代:
其中 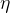 一般被称为“学习率” ,用于控制矢量的长度。如果是要寻找极大值,则 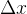 应当沿梯度正方向。
梯度下降算法
因为代码求梯度非常困难,博主手搓不出来,这里只给算法流程
算法流程
- 初始化:
- 循环,直到
- 计算当前点的梯度矢量:
- 更新优化解:
-
- 输出优化解
参数  为收敛精度,值越小,输出解越接近极小值点,同时迭代次数越多。
梯度下降法优缺点
优点:
- 算法简单,只要知道任意一点的梯度矢量就能进行迭代优化
- 在学习率合适的情况下,算法能很好的收敛到极小值点
缺点:
- 对于梯度值较小的区域,收敛速度很慢
- 收敛性依赖于学习率的设置,与初始值选择无关,但目前对于某个具体问题来说,还没有能够直接确定学习率的方法
- 梯度下降只能保证收敛于一个极值点,无法一次计算出所有的极值点,具体收敛到哪个极值点依赖于初始值的设置
- 梯度下降不能保证求得的极小值是全局最小值
参考文献
【1】模式识别 - 刘家锋
【2】数学分析(一)- 崔国辉
版权归原作者 真理Eternal 所有, 如有侵权,请联系我们删除。

