目的:在传统的向量叉乘计算中,常常遇到叉乘。定义为向量。其这个向量方向满足右手定则。它的模大小,一般被忽略。因此推测一下。
向量叉乘定义:
外积(英语:Cross product)又称向量积(英语:Vector product),是对三维空间中的两个向量的二元运算,用符号:
×
\times
×表示。可以定义为:
a
→
×
b
→
=
c
→
(
1
)
\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c} \space \space \space \space(1)
a×b=c (1)
假设两个向量
a
→
×
b
→
\overrightarrow{a} \times \overrightarrow{b}
a×b外积,它的方向为
c
→
\overrightarrow{c}
c。其方向由右手定则决定。模长等于这两个向量边的平行四边形的面积。
它的定义也可以写成:
a
→
×
b
→
=
∣
a
→
∣
∣
b
→
∣
s
i
n
(
θ
)
n
→
(
2
)
\overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|sin(\theta)\overrightarrow{n} \space \space \space \space(2)
a×b=∣a∣∣b∣sin(θ)n (2)
其中
θ
\theta
θ为两个向量的夹角
0
≤
θ
≤
180
0\le \theta \le 180
0≤θ≤180;
∣
a
→
∣
∣
b
→
∣
|\overrightarrow{a}||\overrightarrow{b}|
∣a∣∣b∣分别为两个向量
a
→
b
→
\overrightarrow{a} \overrightarrow{b}
ab的模长。
n
→
\overrightarrow{n}
n为垂直于
a
→
b
→
\overrightarrow{a} \overrightarrow{b}
ab所在平面的法向量,且它满足右手定则。如下图:
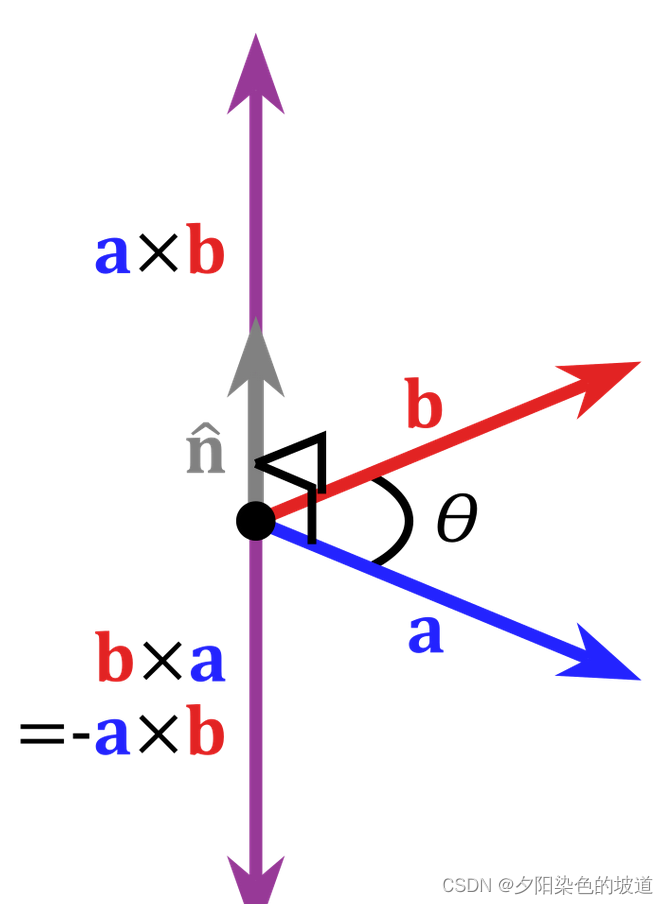
上面的定义很好理解。但是一般在代数计算两个向量的叉乘,会用到行列式计算。就如一组单位积
(
i
→
,
j
→
,
k
→
)
(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})
(i,j,k);其中
a
→
=
a
0
i
→
+
a
1
j
→
+
a
2
k
→
\overrightarrow{a}=a_0\overrightarrow{i}+a_1\overrightarrow{j}+a_2\overrightarrow{k}
a=a0i+a1j+a2k;
b
→
=
b
0
i
→
+
b
1
j
→
+
b
2
k
→
\overrightarrow{b}=b_0\overrightarrow{i}+b_1\overrightarrow{j}+b_2\overrightarrow{k}
b=b0i+b1j+b2k
在计算两个向量的叉乘时候,一般用代数方法为:
a
→
×
b
→
=
(
a
0
i
→
+
a
1
j
→
+
a
2
k
→
)
×
(
b
→
=
b
0
i
→
+
b
1
j
→
+
b
2
k
→
)
=
a
0
b
0
(
i
→
×
i
→
)
+
a
0
b
1
(
i
→
×
j
→
)
+
a
0
b
2
(
i
→
×
k
→
)
+
a
1
b
0
(
j
→
×
i
→
)
+
a
1
b
1
(
j
→
×
j
→
)
+
a
1
b
2
(
j
→
×
k
→
)
+
a
2
b
0
(
k
→
×
i
→
)
+
a
2
b
1
(
k
→
×
j
→
)
+
a
2
b
2
(
k
→
×
k
→
)
(
3
)
\overrightarrow{a} \times \overrightarrow{b} = (a_0\overrightarrow{i}+a_1\overrightarrow{j}+a_2\overrightarrow{k}) \times(\overrightarrow{b}=b_0\overrightarrow{i}+b_1\overrightarrow{j}+b_2\overrightarrow{k}) \\ = a_0b_0(\overrightarrow{i} \times \overrightarrow{i}) + a_0b_1(\overrightarrow{i} \times \overrightarrow{j}) + a_0b_2(\overrightarrow{i} \times \overrightarrow{k})+ \\ a_1b_0(\overrightarrow{j} \times \overrightarrow{i}) + a_1b_1(\overrightarrow{j} \times \overrightarrow{j}) + a_1b_2(\overrightarrow{j} \times \overrightarrow{k}) + \\ a_2b_0(\overrightarrow{k} \times \overrightarrow{i}) + a_2b_1(\overrightarrow{k} \times \overrightarrow{j}) + a_2b_2(\overrightarrow{k} \times \overrightarrow{k}) \space \space \space \space(3)
a×b=(a0i+a1j+a2k)×(b=b0i+b1j+b2k)=a0b0(i×i)+a0b1(i×j)+a0b2(i×k)+a1b0(j×i)+a1b1(j×j)+a1b2(j×k)+a2b0(k×i)+a2b1(k×j)+a2b2(k×k) (3)
因为基向量
(
i
→
,
j
→
,
k
→
)
(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})
(i,j,k)两两垂直,且为单位向量。
0
→
\overrightarrow{0}
0 表示都为
0
0
0的向量。所以得到:
i
→
×
i
→
=
0
→
(
4
)
j
→
×
j
→
=
0
→
(
5
)
k
→
×
k
→
=
0
→
(
6
)
i
→
×
j
→
=
k
→
(
7
)
j
→
×
k
→
=
i
→
(
8
)
k
→
×
i
→
=
j
→
(
9
)
\overrightarrow{i} \times \overrightarrow{i}= \overrightarrow{0} \space \space \space \space(4) \\ \overrightarrow{j} \times \overrightarrow{j}= \overrightarrow{0} \space \space \space \space(5) \\ \overrightarrow{k} \times \overrightarrow{k}=\overrightarrow{0} \space \space \space \space(6) \\ \overrightarrow{i} \times \overrightarrow{j}= \overrightarrow{k} \space \space \space \space(7) \\ \overrightarrow{j} \times \overrightarrow{k}= \overrightarrow{i} \space \space \space \space(8)\\ \overrightarrow{k} \times \overrightarrow{i}= \overrightarrow{j} \space \space \space \space(9)
i×i=0 (4)j×j=0 (5)k×k=0 (6)i×j=k (7)j×k=i (8)k×i=j (9)
将
(
4
)
(
5
)
(
6
)
(
7
)
(
8
)
(
9
)
(4)(5)(6)(7)(8)(9)
(4)(5)(6)(7)(8)(9)代入公式
(
3
)
(3)
(3)得到如下:
a
→
×
b
→
=
−
a
0
b
0
0
→
+
a
0
b
1
k
→
−
a
0
b
2
j
→
−
a
1
b
0
k
→
−
a
1
b
1
0
→
+
a
1
b
2
i
→
+
a
2
b
0
j
→
−
a
2
b
1
i
→
−
a
2
b
2
0
→
=
(
a
1
b
2
−
a
2
b
1
)
i
→
+
(
a
2
b
0
−
a
0
b
2
)
j
→
+
(
a
0
b
1
−
a
1
b
0
)
k
→
(
10
)
\overrightarrow{a} \times \overrightarrow{b} = -a_0b_0\overrightarrow{0}+a_0b_1\overrightarrow{k}-a_0b_2\overrightarrow{j} \\ - a_1b_0\overrightarrow{k}-a_1b_1\overrightarrow{0} +a_1b_2\overrightarrow{i} \\ +a_2b_0 \overrightarrow{j} - a_2b_1\overrightarrow{i} -a_2b_2\overrightarrow{0}\\ =(a_1b_2-a_2b_1)\overrightarrow{i} + (a_2b_0-a_0b_2)\overrightarrow{j} +(a_0b_1-a_1b_0)\overrightarrow{k} \space \space \space \space(10)
a×b=−a0b00+a0b1k−a0b2j−a1b0k−a1b10+a1b2i+a2b0j−a2b1i−a2b20=(a1b2−a2b1)i+(a2b0−a0b2)j+(a0b1−a1b0)k (10)
公式的
(
10
)
(10)
(10),在日常用行列式计算表达。使用
(
i
→
,
j
→
,
k
→
)
(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})
(i,j,k)的矩阵**余子式**计算方式。它和代数计算方式相等。
a
→
×
b
→
=
[
i
→
j
→
k
→
a
0
a
1
a
2
b
0
b
1
b
2
]
=
(
a
1
b
2
−
a
2
b
1
)
i
→
+
(
a
2
b
0
−
a
0
b
2
)
j
→
+
(
a
0
b
1
−
a
1
b
0
)
k
→
\overrightarrow{a} \times \overrightarrow{b} =\begin{bmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_0& a_1 & a_2 \\ b_0& b_1 & b_2 \end{bmatrix} = (a_1b_2-a_2b_1)\overrightarrow{i} + (a_2b_0-a_0b_2)\overrightarrow{j} +(a_0b_1-a_1b_0)\overrightarrow{k}
a×b=⎣⎡ia0b0ja1b1ka2b2⎦⎤=(a1b2−a2b1)i+(a2b0−a0b2)j+(a0b1−a1b0)k
因为它为基向量,在欧式几何中,它的表达为:
i
→
=
[
1
0
0
]
;
j
→
=
[
0
1
0
]
;
k
→
=
[
0
0
1
]
(
11
)
\overrightarrow{i}=\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}; \overrightarrow{j}=\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix};\overrightarrow{k}=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \space \space \space \space(11)
i=⎣⎡100⎦⎤;j=⎣⎡010⎦⎤;k=⎣⎡001⎦⎤ (11)
因此
(
11
)
(11)
(11)代入到
(
10
)
(10)
(10)得到:
a
→
×
b
→
=
[
a
1
b
2
−
a
2
b
1
a
2
b
0
−
a
0
b
2
a
0
b
1
−
a
1
b
0
]
(
12
)
\overrightarrow{a} \times \overrightarrow{b} = \begin{bmatrix} a_1b_2-a_2b_1 \\ a_2b_0-a_0b_2 \\ a_0b_1-a_1b_0 \end{bmatrix} \space \space \space \space(12)
a×b=⎣⎡a1b2−a2b1a2b0−a0b2a0b1−a1b0⎦⎤ (12)
上面是基于基向量的表达,它和上面的公式对应,因此可以得到:
a
→
×
b
→
=
∣
a
→
∣
∣
b
→
∣
s
i
n
(
θ
)
n
→
=
[
a
1
b
2
−
a
2
b
1
a
2
b
0
−
a
0
b
2
a
0
b
1
−
a
1
b
0
]
(
13
)
\overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|sin(\theta)\overrightarrow{n} =\begin{bmatrix} a_1b_2-a_2b_1 \\ a_2b_0-a_0b_2 \\ a_0b_1-a_1b_0 \end{bmatrix} \space \space \space \space(13)
a×b=∣a∣∣b∣sin(θ)n=⎣⎡a1b2−a2b1a2b0−a0b2a0b1−a1b0⎦⎤ (13)
在一些应用,经常向量的表示转化为矩阵的运算。因此(13)公式可以表示矩阵和向量的乘法。
a
→
×
b
→
=
∣
a
→
∣
∣
b
→
∣
s
i
n
(
θ
)
n
→
=
[
a
1
b
2
−
a
2
b
1
a
2
b
0
−
a
0
b
2
a
0
b
1
−
a
1
b
0
]
=
[
0
−
a
2
a
1
a
2
0
−
a
0
−
a
1
a
0
0
]
[
b
0
b
1
b
2
]
=
a
→
×
b
→
(
14
)
\overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|sin(\theta)\overrightarrow{n} =\begin{bmatrix} a_1b_2-a_2b_1 \\ a_2b_0-a_0b_2 \\ a_0b_1-a_1b_0 \end{bmatrix} = \begin{bmatrix} 0 & -a_2 & a_1 \\ a_2& 0 & -a_0 \\ -a_1& a_0 & 0 \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \end{bmatrix} = \overrightarrow{a} \times \overrightarrow{b} \space \space \space \space(14)
a×b=∣a∣∣b∣sin(θ)n=⎣⎡a1b2−a2b1a2b0−a0b2a0b1−a1b0⎦⎤=⎣⎡0a2−a1−a20a0a1−a00⎦⎤⎣⎡b0b1b2⎦⎤=a×b (14)
两个向量的叉乘仅仅在三维空间有定义。在二维空间没有定义。
下面介绍向量的行列式和向量组成的平行四边形面积的关系。
假设
a
→
,
b
→
\overrightarrow{a} ,\overrightarrow{b}
a,b为二维向量。这样易于解释。因此画图如下:
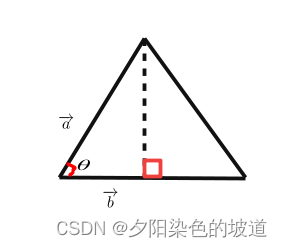
计算三角形面积为:
∣
a
r
e
a
∣
=
1
2
∣
a
→
∣
∣
b
→
∣
s
i
n
(
θ
)
(
15
)
|area|=\cfrac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|sin(\theta) \space \space \space \space(15)
∣area∣=21∣a∣∣b∣sin(θ) (15)
转化一下表达,因为
s
i
n
(
θ
)
sin(\theta)
sin(θ)不好计算,需要计算
c
o
s
(
θ
)
cos(\theta)
cos(θ)。
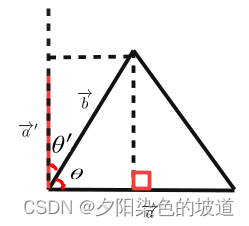
其中
∣
a
→
′
∣
=
∣
a
→
∣
|\overrightarrow{a}'|=|\overrightarrow{a}|
∣a′∣=∣a∣;
∣
b
→
∣
s
i
n
(
θ
)
=
∣
b
→
′
∣
c
o
s
(
θ
′
)
|\overrightarrow{b}|sin(\theta)=|\overrightarrow{b}'|cos(\theta')
∣b∣sin(θ)=∣b′∣cos(θ′);
∣
a
r
e
a
∣
=
1
2
∣
a
→
∣
∣
b
→
∣
s
i
n
(
θ
)
=
1
2
∣
b
→
∣
∣
a
→
∣
c
o
s
(
θ
′
)
(
16
)
|area|=\cfrac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|sin(\theta)=\cfrac{1}{2}|\overrightarrow{b}||\overrightarrow{a}|cos(\theta') \space \space \space \space(16)
∣area∣=21∣a∣∣b∣sin(θ)=21∣b∣∣a∣cos(θ′) (16)
其中
θ
′
+
θ
=
90
\theta'+\theta=90
θ′+θ=90.且
∣
a
→
′
∣
=
∣
a
→
∣
|\overrightarrow{a}'|=|\overrightarrow{a}|
∣a′∣=∣a∣,容易得到公式简化,简化上述等式为:
∣
a
r
e
a
∣
=
1
2
∣
b
→
∣
∣
a
→
′
∣
c
o
s
(
θ
′
)
=
1
2
b
→
⋅
a
→
′
=
1
2
a
→
′
⋅
b
→
(
17
)
|area|=\cfrac{1}{2}|\overrightarrow{b}||\overrightarrow{a}'|cos(\theta')=\cfrac{1}{2}\overrightarrow{b} \cdot \overrightarrow{a}'=\cfrac{1}{2}\overrightarrow{a}' \cdot \overrightarrow{b} \space \space \space \space(17)
∣area∣=21∣b∣∣a′∣cos(θ′)=21b⋅a′=21a′⋅b (17)
因为
a
→
′
\overrightarrow{a}'
a′是通过
a
→
\overrightarrow{a}
a旋转90度得到的,如下图。
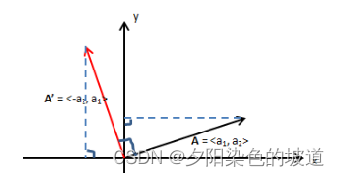
因此假设
a
→
=
[
a
0
a
1
]
\overrightarrow{a}=\begin{bmatrix} a_0 \\ a_1 \end{bmatrix}
a=[a0a1] 得到
a
→
′
=
[
−
a
1
a
0
]
\overrightarrow{a}'=\begin{bmatrix} -a_1 \\ a_0 \end{bmatrix}
a′=[−a1a0]
因此得到公式:
2
∣
a
r
e
a
∣
=
a
→
′
⋅
b
→
=
[
−
a
1
a
0
]
⋅
[
b
0
b
1
]
=
a
0
b
1
−
a
1
b
0
(
18
)
2|area|=\overrightarrow{a}' \cdot \overrightarrow{b}=\begin{bmatrix} -a_1 \\ a_0 \end{bmatrix} \cdot \begin{bmatrix} b_0 \\ b_1 \end{bmatrix} = a_0b_1-a_1b_0 \space \space \space \space(18)
2∣area∣=a′⋅b=[−a1a0]⋅[b0b1]=a0b1−a1b0 (18)
可以看到行列式是面积的表达。
2
∣
a
r
e
a
∣
=
∣
a
0
a
1
b
0
b
1
∣
2|area|=\begin{vmatrix} a_0 & a_1 \\ b_0 & b_1 \end{vmatrix}
2∣area∣=∣∣a0b0a1b1∣∣
版权归原作者 夕阳染色的坡道 所有, 如有侵权,请联系我们删除。