交叉验证(Cross Validation)和网格搜索(Grid Search)常结合在一起并用来筛选模型的最优参数。本文将从零开始一步步讲解交叉验证和网格搜索的由来,并基于sklearn实现它们。
目录
一、交叉验证法
1.1 交叉验证法的由来
在机器学习中,我们通常是将已有的数据集(Data Set)一分为二(不一定等分),一部分是训练集(Training Set),一部分是测试集(Test Set)。通常,我们会在训练集上训练模型(Model),然后在测试集上评估模型的性能(Performance)。评估性能需要用到性能度量(Performance Measure),即衡量模型好坏的指标。本文将使用准确率(accuracy)作为性能度量。
以软间隔SVM为例,其中的参数
C
C
C 需要事先给定,我们将这种需要事先给定的参数称为**超参数**(Hyperparameter)。如果选用高斯核、多项式核、Sigmoid核,则其中的参数
γ
,
r
,
d
\gamma, r, d
γ,r,d 也是超参数。我们**先只考虑线性核**,也就是**只有一个超参数**的情形。
首先将数据集分为训练集和测试集,这个时候训练集和测试集已经固定了:

对于每个固定的
C
C
C,我们在训练集上训练都会得到一个软间隔SVM模型,然后在测试集上评估该模型的分类准确率。如果准确率高,我们就说模型是好的,反之则较差。我们自然是想找到使得分类准确率最高的那个
C
C
C,因为它对应的模型是最好的。寻找 “最好” 的
C
C
C 的这一过程称为**调参**(Parameter Tuning),即不断调整参数使得训练出来的模型最优,“最好” 的
C
C
C 也称为**最优参数**(Best Parameter)。
为了叙述方便起见,我们接下来将模型在测试集上的分类准确率称为得分(Score)。此外,因为当确定参数
C
C
C 后,模型也就随之确定了,即参数和模型之间是一个**一一对应**的关系,所以我们后续也会使用 “**参数的得分**” 这种说法。
假设我们已经找到了最优参数:
C
b
e
s
t
C_{best}
Cbest,它所对应的模型的得分最高。现在,我们想测试这个最优模型的泛化能力,可**已经没有数据供我们测试了**。如果还在测试集上去测试这个最优模型的性能,那无疑是**重复劳动**,因为我们在调参的过程中就已经在测试集上测试了每个模型的性能。另一方面,因为我们的
C
C
C 是根据模型在测试集上的得分来进行选取的,也就是说,测试集中的 “知识” 已经渗入到了我们的最优模型当中,这就会导致**过拟合**,从而降低了模型的泛化能力。
解决该问题的一个方法就是,将原先的训练集一分为二,一部分用作训练集,一部分用作验证集(Validation Set)。验证集用来选择最优参数,得到最优参数后再在原先的训练集上重新训练,得到的模型在测试集上评估最终性能(Final Evaluation)。

因为我们在得到最优参数之前都是在验证集上对每个模型(参数)进行打分的,得分最高的成为最优参数。换句话说,最优参数与验证集有关。而验证集是从原先的训练集划分得来,这种划分具有一定的偶然性,这就可能导致我们的最优参数是在众多参数之中 “侥幸” 取胜,即最优参数更适合这个验证集,如果换成另外一个验证集,它可能就不是最优的了。
举个例子,设原先的训练集为
T
T
T,考虑两种划分方式:
T
=
(
T
\
V
1
)
⋃
V
1
T=(T\backslash V_1)\,\bigcup\, V_1
T=(T\V1)⋃V1,
T
=
(
T
\
V
2
)
⋃
V
2
T=(T\backslash V_2)\,\bigcup\, V_2
T=(T\V2)⋃V2,其中
V
1
,
V
2
V_1, V_2
V1,V2 是**不同**的验证集,
T
\
V
1
,
T
\
V
2
T\backslash V_1, T\backslash V_2
T\V1,T\V2 是训练集,则可能会出现:
- 验证集为 V 1 V_1 V1 时,最优参数为 C = 1 C=1 C=1,最差参数为 C = 1000 C=1000 C=1000
- 验证集为 V 2 V_2 V2 时,最优参数为 C = 1000 C=1000 C=1000,最差参数为 C = 1 C=1 C=1
那么如何减少这种偶然性呢?直观来看,应该取多个验证集
V
1
,
V
2
,
⋯
,
V
m
V_1, V_2,\cdots, V_m
V1,V2,⋯,Vm,参数在每个验证集
V
i
V_i
Vi 上都会有一个得分
S
i
S_i
Si,这些得分的平均
S
‾
=
(
S
1
+
⋯
+
S
m
)
/
m
\overline{S}=(S_1+\cdots+S_m)/m
S=(S1+⋯+Sm)/m 就作为这个参数的得分。
注意到验证集是从原先的训练集划分得来,即
V
i
⊂
T
,
i
=
1
,
⋯
,
m
V_i\subset T,\; i=1,\cdots,m
Vi⊂T,i=1,⋯,m,为了进一步减少偶然性,很自然的一个想法就是把原先的训练集全部用上并要求验证集两两互斥且大小相等,即:
T
=
V
1
∪
V
2
∪
⋯
∪
V
m
,
∣
V
1
∣
=
∣
V
2
∣
=
⋯
=
∣
V
m
∣
,
V
i
∩
V
j
=
∅
(
i
≠
j
)
T=V_1\, \cup\, V_2\, \cup\cdots\cup\, V_m,\quad |V_1|=|V_2|=\cdots=|V_m|,\quad V_i\,\cap\, V_j=\varnothing(i\neq j)
T=V1∪V2∪⋯∪Vm,∣V1∣=∣V2∣=⋯=∣Vm∣,Vi∩Vj=∅(i=j)
这样我们就得到了
m
m
m 组训练集
/
/
/验证集,对于每一个参数,它的得分就是在这
m
m
m 个验证集上得分的**均值**:
T
=
(
T
\
V
1
)
∪
V
1
⇒
S
1
T
=
(
T
\
V
2
)
∪
V
2
⇒
S
2
⋮
⋮
T
=
(
T
\
V
m
)
∪
V
m
⇒
S
m
⟹
S
‾
=
S
1
+
⋯
+
S
m
m
\begin{aligned} T=(T\backslash V_1)\,\cup\, V_1 \quad\Rightarrow\quad &S_1 \\ T=(T\backslash V_2)\,\cup\, V_2 \quad\Rightarrow\quad &S_2\\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\vdots\quad\quad\quad\quad\quad\quad\quad\vdots \\ T=(T\backslash V_m)\,\cup\, V_m \quad\Rightarrow\quad &S_m \\ \end{aligned} \quad\Longrightarrow\quad \overline{S}=\frac{S_1+\cdots +S_m}{m}
T=(T\V1)∪V1⇒T=(T\V2)∪V2⇒T=(T\Vm)∪Vm⇒S1S2⋮⋮Sm⟹S=mS1+⋯+Sm
S
‾
\overline{S}
S**最高的参数成为我们的最优参数**,下面的图更形象的展示了这一过程:
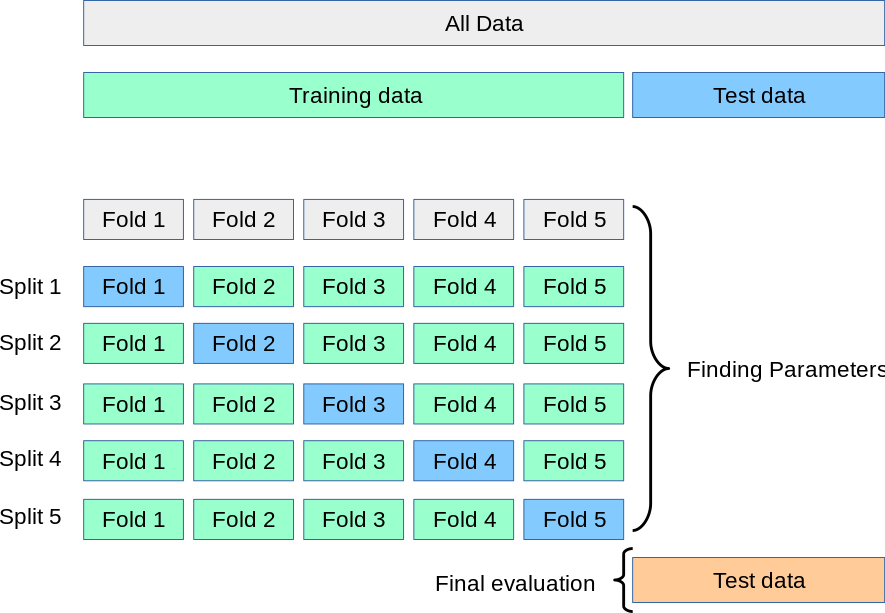
得到最优参数后,我们再在原先的训练集上重新训练,完整的流程图如下:
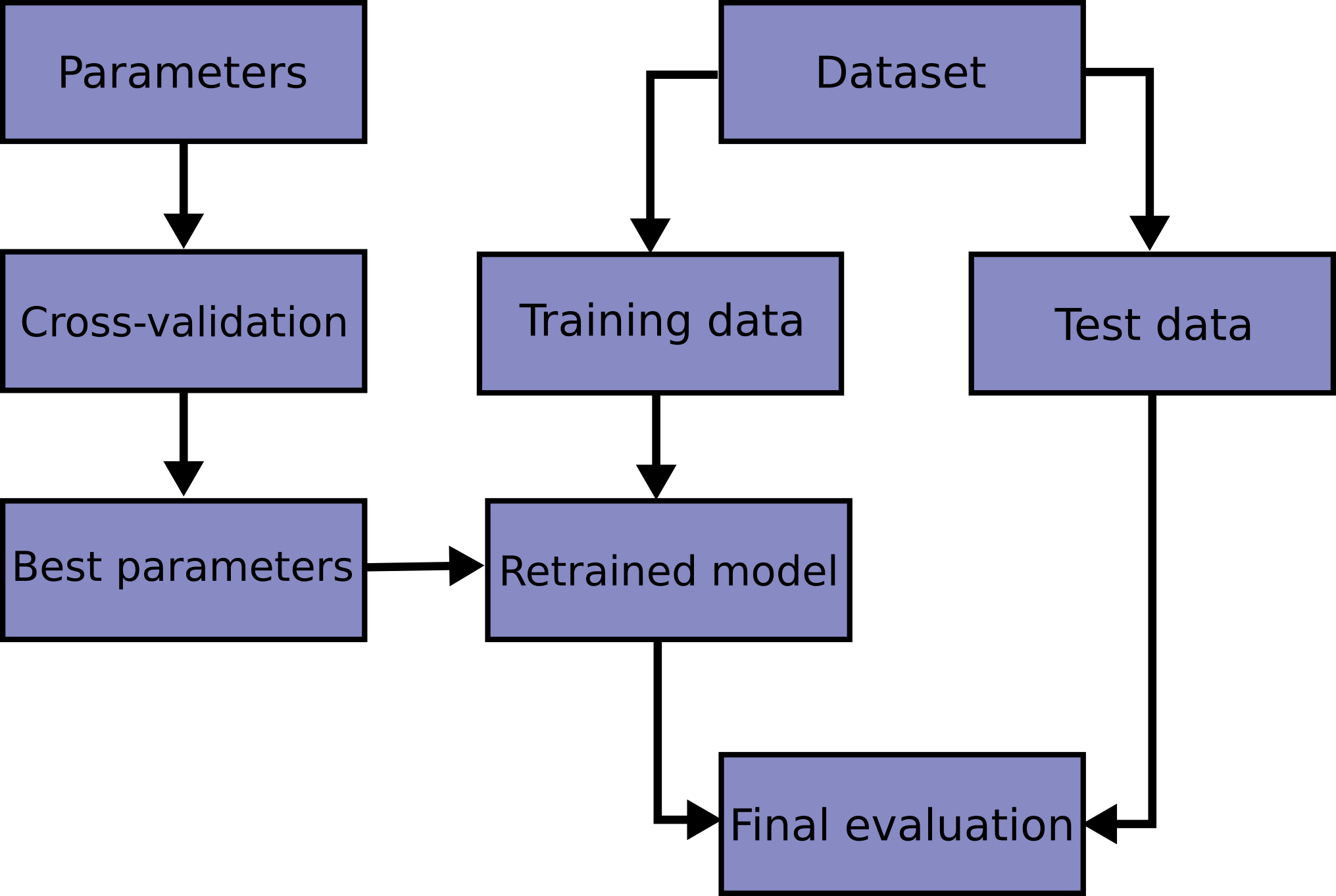
很多时候,我们的
T
T
T 做不到
m
m
m 等分,那只能退而求其次,要求
∣
V
1
∣
≈
∣
V
2
∣
≈
⋯
≈
∣
V
m
∣
|V_1|\approx|V_2|\approx\cdots\approx|V_m|
∣V1∣≈∣V2∣≈⋯≈∣Vm∣
这便是交叉验证法。
1.2 交叉验证法的定义
(
交
叉
验
证
法
)
\textcolor{purple}{(交叉验证法)}\;
(交叉验证法) 将数据集
D
D
D(原先的训练集)划分为
k
k
k 个大小**相似**的**互斥**子集。每个子集
D
i
D_i
Di 尽可能**保持数据分布的一致性**,即从
D
D
D 中通过**分层采样**得到。然后每次用
k
−
1
k - 1
k−1 个子集的并集作为训练集,余下的那个子集作为验证集;这样就可以获得
k
k
k 组训练
/
/
/验证集,从而可以进行
k
k
k 次训练和验证,最终返回的是这
k
k
k 个结果的**均值**。 该方法又称为 **
k
k
k 折交叉验证**(k-fold cross validation),
k
k
k 常用的取值为
5
,
10
,
20
5,10,20
5,10,20 等。
(
留
一
法
)
\textcolor{purple}{(留一法)}\;
(留一法) 若
k
=
∣
D
∣
k=|D|
k=∣D∣,则得到了交叉验证法的一个特例:**留一法**(Leave-One-Out,简称LOO)。LOO使用的训练集与初始数据集相比只少了一个样本,这就使得在绝大多数情况下,LOO中被实际评估的模型与期望评估的用
D
D
D 训练出的模型很相似。因此,LOO的评估结果往往被认为比较准确。但LOO也有缺陷:
∣
D
∣
|D|
∣D∣ 较大时,训练
∣
D
∣
|D|
∣D∣ 个模型的计算开销可能是难以忍受的(这还是在未考虑调参的情况下)。
1.3 sklearn.model_selection.train_test_split()
该函数的主要作用是将现有的数据集随机划分成训练集和测试集,其主要参数如下:
t
r
a
i
n
_
t
e
s
t
_
s
p
l
i
t
(
X
,
y
,
t
e
s
t
_
s
i
z
e
=
N
o
n
e
,
t
r
a
i
n
_
s
i
z
e
=
N
o
n
e
,
r
a
n
d
o
m
_
s
t
a
t
e
=
N
o
n
e
)
\mathrm{train\_test\_split(X, y, test\_size=None, train\_size=None, random\_state=None)}
train_test_split(X,y,test_size=None,train_size=None,random_state=None)
参数描述X示例矩阵y标签向量test_size可以为浮点数或整数;当为浮点数时,表示测试集在整个数据集中所占的比例。当为整数时,表示测试集的大小;当test_size和train_size都为None时,test_size默认调整至0.25train_size同上;当train_size为None时,默认调整至测试集的补集的大小
对示例矩阵和标签向量不了解的读者可参考我的上一篇文章。
该函数会返回一个列表
[
X
_
t
r
a
i
n
,
X
_
t
e
s
t
,
y
_
t
r
a
i
n
,
y
_
t
e
s
t
]
[X\_train, X\_test, y\_train, y\_test]
[X_train,X_test,y_train,y_test],我们只需要用相应的四个参数去接收即可。
from sklearn.model_selection import train_test_split
X =[[1,2],[2,3],[3,3],[2,1],[3,2]]
y =[1,1,1,-1,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)print(X_train)# [[3, 3], [1, 2], [2, 1]]print(X_test)# [[2, 3], [3, 2]]print(y_train)# [1, 1, -1]print(y_test)# [1, -1]
1.4 sklearn.metrics.accuracy_score()
在进一步讲解有关交叉验证的函数之前,我们先来讲一下有关性能度量的函数。
我们已经知道,SVC类的score方法
clf.score()
可以用来计算模型在测试集上的分类准确率,例如:
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
X, y = make_blobs(n_samples=500, centers=2, random_state=34)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
clf = SVC(kernel='linear')
clf.fit(X_train, y_train)print(clf.score(X_test, y_test))# 0.912
即分类准确率为
91.2
%
91.2\%
91.2%。
accuracy_score的使用方法:
a
c
c
u
r
a
c
y
_
s
c
o
r
e
(
y
_
t
r
u
e
,
y
_
p
r
e
d
)
\mathrm{accuracy\_score(y\_true, y\_pred)}
accuracy_score(y_true,y_pred)。其中
y_true
是真实的标签列表,而
y_pred
是预测的标签列表。
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
X, y = make_blobs(n_samples=500, centers=2, random_state=34)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
clf = SVC(kernel='linear')
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)print(accuracy_score(y_test, y_pred))# 0.912
看到这里,可能会有读者疑惑,
clf.score
和
accuracy_score
的结果一样,那它们之间到底有什么区别呢?
1.4.1 clf.score 与 accuracy_score 的区别
不严谨地来讲,
accuracy_score
仅仅是按序比较两个列表(
array_like
对象),然后返回相同元素的个数所占的比例:
from sklearn.metrics import accuracy_score
A =[1,2,3,4]
B =[2,2,3,5]
C =[4,3,2,1]print(accuracy_score(A, B))# 0.5print(accuracy_score(A, C))# 0.4
从第二个输出可以看出,虽然两个列表的内容相同,但因为
accuracy_score
是按序(索引)进行比较的,所以准确率为
0
0
0;从第一个输出可以看出,两个列表只有索引
1
1
1 和
2
2
2 处的元素相同,所以准确率为
2
/
4
=
0.5
2/4=0.5
2/4=0.5。
再来看看
clf.score
,其底层实现为
defscore(self, X, y, sample_weight=None):from.metrics import accuracy_score
return accuracy_score(y, self.predict(X), sample_weight=sample_weight)
可以看出本质上和
accuracy_score
没有什么区别,但
clf.score
使用起来更为方便,因此更加推荐。
1.5 sklearn.model_selection.cross_val_score()
我们已经知道,
k
k
k 折交叉验证一共会产生
k
k
k 个得分(这些得分的**均值**作为交叉验证的得分),而
cross_val_score()
返回的就是这
k
k
k 个得分。
该函数主要有以下参数:
c
r
o
s
s
_
v
a
l
_
s
c
o
r
e
(
e
s
t
i
m
a
t
o
r
,
X
,
y
,
s
c
o
r
i
n
g
=
N
o
n
e
,
c
v
=
N
o
n
e
)
\mathrm{cross\_val\_score(estimator, X, y, scoring=None, cv=None)}
cross_val_score(estimator,X,y,scoring=None,cv=None)
参数描述estimatorSVM任务下就是SVC实例scoring性能度量;默认值为None,即采用SVC类中的score方法;有关scoring的可选参数请见官方文档cv
k
k
k 折交叉验证中的
k
k
k;默认值为None,即采用
5
5
5 折交叉验证
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
X, y = make_blobs(n_samples=500, centers=2, random_state=34)
clf = SVC(kernel='linear')print(cross_val_score(clf, X, y, cv=3))# [0.94011976 0.94011976 0.93373494]print(cross_val_score(clf, X, y, cv=3, scoring='accuracy'))# [0.94011976 0.94011976 0.93373494]
该例子也进一步说明了
clf.score
和
accuracy_score
是一样的。
scores = cross_val_score(clf, X, y, cv=3)print("%.4f accuracy with a standard deviation of %.4f"%(scores.mean(), scores.std()))# 0.938 accuracy with a standard deviation of 0.003
即我们交叉验证的得分为
0.938
0.938
0.938。
基于此,我们可以使用
cross_val_score
来选择最优参数:
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
X, y = make_blobs(n_samples=500, centers=2, random_state=34)for C in[1,10,100,1000,10000,100000]:
clf = SVC(C=C, kernel='linear')
scores = cross_val_score(clf, X, y, cv=4)# 四折交叉验证print('C: %d, accuracy: %.3f'%(C, scores.mean()))# C: 1, accuracy: 0.936# C: 10, accuracy: 0.936# C: 100, accuracy: 0.936# C: 1000, accuracy: 0.938# C: 10000, accuracy: 0.938# C: 100000, accuracy: 0.940
从输出结果可以看出,
C
=
100000
C=100000
C=100000 是这六个参数中的最优参数(不过要注意的是,我们是直接将原有的数据集划分为训练集和验证集,并未划分出测试集)。
正确的流程应该是:先将原有的数据集划分为训练集和测试集,在训练集上进行
k
k
k 折交叉验证来选取最优参数,得到最优参数后,在训练集上训练模型,在测试集上测试性能,完整的代码如下:
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
# 初始化
X, y = make_blobs(n_samples=500, centers=2, random_state=34)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
params =[1,10,100,1000,10000,100000,1000000]
params_score =[]# 寻找最优参数for C in params:
clf = SVC(C=C, kernel='linear')
scores = cross_val_score(clf, X_train, y_train, cv=4)
params_score.append(scores.mean())
best_param = params[params_score.index(max(params_score))]# 重新训练
clf_best = SVC(C=best_param, kernel='linear')
clf_best.fit(X_train, y_train)# 测试性能
accuracy = clf_best.score(X_test, y_test)print(best_param)# 1000000print(accuracy)# 0.95
可以看出,我们使用最优参数训练出来的模型在测试集上的分类准确率为
95
%
95\%
95%。
二、网格搜索法
网格搜索法的本质是遍历。
2.1 网格搜索法的由来
在训练线性核软间隔SVM时,会涉及到超参数
C
C
C,选取合适的
C
C
C 值能够使我们训练出来的模型最优,那么该如何去寻找这个最合适的
C
C
C 值呢?
一个很自然的想法就是把
C
C
C 的所有取值都试一遍,用交叉验证法对每一个
C
C
C 值打分,得分最高的
C
C
C 成为我们的最优参数。但现实中,我们的参数一般都是连续取值的,我们不可能去遍历所有的
C
C
C 值,因此只能考虑有限个
C
C
C 值。考虑到
C
C
C 一般较大,我们可以假设
C
C
C 的取值集合为
C
=
{
1
,
10
,
1
0
2
,
⋯
,
1
0
6
}
\boldsymbol C=\{1,10,10^2,\cdots,10^6\}
C={1,10,102,⋯,106}
于是我们只需要去遍历集合
C
\boldsymbol C
C。
现在考虑高斯核的情形,这时候会涉及到两个参数:
(
C
,
γ
)
(C,\gamma)
(C,γ)。因为
γ
\gamma
γ 取值一般较小,我们可以假设它的取值集合为
γ
=
{
1
0
−
6
,
1
0
−
5
,
⋯
,
1
0
−
1
,
1
}
\boldsymbol \gamma =\{10^{-6}, 10^{-5},\cdots,10^{-1},1\}
γ={10−6,10−5,⋯,10−1,1}
现在作笛卡尔积
C
×
γ
\boldsymbol C\times \boldsymbol\gamma
C×γ,则该集合的大小为
∣
C
∣
⋅
∣
γ
∣
|\boldsymbol C|\cdot|\boldsymbol \gamma|
∣C∣⋅∣γ∣,且其中元素的形式为
(
C
,
γ
)
(C,\gamma)
(C,γ)。遍历
C
×
γ
\boldsymbol C\times \boldsymbol\gamma
C×γ 就相当于遍历
(
C
,
γ
)
(C,\gamma)
(C,γ) 所有可能的组合。注意到
C
×
γ
\boldsymbol C\times \boldsymbol\gamma
C×γ 还可以用 “网格” 来进行表示:
C
=
1
C=1
C=1
C
=
10
C=10
C=10
⋯
\cdots
⋯
C
=
1
0
6
C=10^6
C=106
γ
=
1
0
−
6
\gamma=10^{-6}
γ=10−6
(
C
=
1
,
γ
=
1
0
−
6
)
(C=1, \gamma=10^{-6})
(C=1,γ=10−6)
(
C
=
10
,
γ
=
1
0
−
6
)
(C=10, \gamma=10^{-6})
(C=10,γ=10−6)
⋯
\cdots
⋯
(
C
=
1
0
6
,
γ
=
1
0
−
6
)
(C=10^6, \gamma=10^{-6})
(C=106,γ=10−6)
γ
=
1
0
−
5
\gamma=10^{-5}
γ=10−5
(
C
=
1
,
γ
=
1
0
−
5
)
(C=1, \gamma=10^{-5})
(C=1,γ=10−5)
(
C
=
10
,
γ
=
1
0
−
5
)
(C=10, \gamma=10^{-5})
(C=10,γ=10−5)
⋯
\cdots
⋯
(
C
=
1
0
6
,
γ
=
1
0
−
5
)
(C=10^6, \gamma=10^{-5})
(C=106,γ=10−5)
⋮
\vdots
⋮
⋮
\vdots
⋮
⋮
\vdots
⋮
⋯
\cdots
⋯
⋮
\vdots
⋮
γ
=
1
\gamma=1
γ=1
(
C
=
1
,
γ
=
1
)
(C=1, \gamma=1)
(C=1,γ=1)
(
C
=
10
,
γ
=
1
)
(C=10, \gamma=1)
(C=10,γ=1)
⋯
\cdots
⋯
(
C
=
1
0
6
,
γ
=
1
)
(C=10^6, \gamma=1)
(C=106,γ=1)
因此遍历
C
×
γ
\boldsymbol C\times \boldsymbol\gamma
C×γ 就相当于遍历上面的网格,又因为我们需要在网格中找出最优参数,故该方法又称**网格搜索法**。
不难看出,网格搜索法的本质就是暴力遍历,即把每一种情况都试一遍,然后找出最优的那个。
2.2 使用 for 循环实现网格搜索
因为网格搜索的本质是遍历,所以我们完全可以使用
for
循环来实现这种遍历。
事实上,1.5 节中的最后一个例子就用到了网格搜索法,不过我们当时也仅仅是遍历了一个参数的取值集合。现在我们考虑两个参数的情形,即使用高斯核的软间隔SVM。
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
# 初始化
X, y = make_blobs(n_samples=500, centers=2, random_state=34)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
best_score =0# 寻找最优参数for C in[1,1e1,1e2,1e3,1e4,1e5,1e6]:for gamma in[1e-6,1e-5,1e-4,1e-3,1e-2,1e-1,1]:
clf = SVC(C=C, gamma=gamma)
cv_scores = cross_val_score(clf, X_train, y_train, cv=4)
current_score = cv_scores.mean()if current_score > best_score:
best_score = current_score
best_parameters ={'C': C,'gamma': gamma}# 重新训练
clf_best = SVC(**best_parameters)
clf_best.fit(X_train, y_train)# 测试性能
accuracy = clf_best.score(X_test, y_test)print(best_parameters)# {'C': 100000.0, 'gamma': 0.01}print(accuracy)# 0.94
输出结果表明,最优参数为
(
C
=
100000
,
γ
=
0.01
)
(C=100000, \gamma=0.01)
(C=100000,γ=0.01),最终的分类准确率为
94
%
94\%
94%。
2.3 sklearn.model_selection.GridSearchCV()
看到这里可能有读者会想,虽然
for
循环是可以实现网格搜索,那有没有更简便快捷的方法呢?好在 sklearn 提供了这样的一个类:
sklearn.model_selection.GridSearchCV
,它结合了网格搜索与交叉验证,能够方便地给出你想要的结果。
2.3.1 参数
创建一个 GridSearchCV 实例常用到以下参数:
G
r
i
d
S
e
a
r
c
h
C
V
(
e
s
t
i
m
a
t
o
r
,
p
a
r
a
m
_
g
r
i
d
,
s
c
o
r
i
n
g
=
N
o
n
e
,
r
e
f
i
t
=
T
r
u
e
,
c
v
=
N
o
n
e
)
\mathrm{GridSearchCV(estimator, param\_grid, scoring=None, refit=True,cv=None)}
GridSearchCV(estimator,param_grid,scoring=None,refit=True,cv=None)
e
s
t
i
m
a
t
o
r
:
\textcolor{blue}{\mathrm{estimator:}}
estimator:
在SVM场景下,
estimator
指的是SVC实例。因为后续我们还需要向
GridSearchCV()
中传入参数网格,所以创建SVC实例的时候不需要任何参数,即:
estimator = SVC()
clf = GridSearchCV(estimator,...)
甚至可以更简便地写成
clf = GridSearchCV(SVC(),...)
p
a
r
a
m
_
g
r
i
d
:
\textcolor{blue}{\mathrm{param\_grid:}}
param_grid:
参数网格,可以为字典或字典列表。
例如对于2.2节中的例子,我们的参数网格就是一个字典:
param_grid ={'C':[1,1e1,1e2,1e3,1e4,1e5,1e6],'gamma':[1e-6,1e-5,1e-4,1e-3,1e-2,1e-1,1],}
该情形一共有
7
×
7
=
49
7\times7=49
7×7=49 种参数组合。
对于某些复杂的任务,我们可能需要用到字典列表:
param_grid =[{"kernel":["rbf"],"gamma":[1e-3,1e-4],"C":[1,10,100,1000]},{"kernel":["linear"],"C":[1,10,100,1000]},]
该情形一共有
1
×
2
×
4
+
1
×
4
=
12
1\times 2\times4\,+\,1\times 4=12
1×2×4+1×4=12 种参数组合。
s
c
o
r
i
n
g
:
\textcolor{blue}{\mathrm{scoring:}}
scoring:
性能度量,默认值为None。常用参数为
'accuracy'
。
r
e
f
i
t
:
\textcolor{blue}{\mathrm{refit:}}
refit:
默认值为
True
。
refit 为
True
时,程序会使用得到的最优参数在原先的训练集上重新训练,结果会存储在
GridSearchCV
实例的
best_estimator_
属性中(注意,
best_estimator_
是已经拟合了的
estimator
)。
2.3.2 方法
本小节仅列出最常用的三个方法,其他方法可自行参阅官方文档。
方法描述fit(X, y)基于所有参数组合拟合estimatorpredict(X)使用最优模型预测样本;当
refit=True
时才可用score(X_test, y_test)除非
scoring
给定,否则采用
best_estimator_.score
方法计算得分
现在,我们将使用
GridSearchCV
来简化2.2节中的代码。
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
X, y = make_blobs(n_samples=500, centers=2, random_state=34)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
param_grid ={'C':[1,1e1,1e2,1e3,1e4,1e5,1e6],'gamma':[1e-6,1e-5,1e-4,1e-3,1e-2,1e-1,1],}
clf = GridSearchCV(SVC(), param_grid, cv=4)
clf.fit(X_train, y_train)print(clf.score(X_test, y_test))# 0.94
输出结果与2.2节中的一致,但代码大大得到了简化。
2.3.3 属性
这里仅列出常用的属性。
属性描述cv_results_以字典形式返回交叉验证的结果best_estimator_使用最优参数在原先的训练集上重新训练得到的estimatorbest_score_best_estimator的交叉验证的得分(均值)best_params_best_estimator中的参数best_index_best_params在
clf.cv_results_['params']
中的索引
接下来我们通过一些例子进一步熟悉这些属性。
为了简便起见,我们将参数网格设置的 “小” 一点,其他不变
......
param_grid ={'C':[1e4,1e5],'gamma':[1e-2,1e-1],}......print(clf.cv_results_)
输出为:
{'mean_fit_time': array([0.00424391,0.01795793,0.02118272,0.12142873]),'std_fit_time': array([0.00044348,0.00522967,0.00470208,0.01951696]),'mean_score_time': array([0.,0.00074494,0.0007624,0.00074446]),'std_score_time': array([0.,0.00043013,0.00044034,0.00042986]),'param_C': masked_array(data=[10000.0,10000.0,100000.0,100000.0],
mask=[False,False,False,False], fill_value='?', dtype=object),'param_gamma': masked_array(data=[0.01,0.1,0.01,0.1],
mask=[False,False,False,False], fill_value='?', dtype=object),'params':[{'C':10000.0,'gamma':0.01},{'C':10000.0,'gamma':0.1},{'C':100000.0,'gamma':0.01},{'C':100000.0,'gamma':0.1}],'split0_test_score': array([0.94,0.94,0.95,0.94]),'split1_test_score': array([0.93,0.95,0.94,0.94]),'split2_test_score': array([0.97,0.95,0.98,0.95]),'split3_test_score': array([0.94,0.94,0.93,0.93]),'mean_test_score': array([0.945,0.945,0.95,0.94]),'std_test_score': array([0.015,0.005,0.01870829,0.00707107]),'rank_test_score': array([2,2,1,4])}
注意:
'params'中存储了所有的参数组合。mean_fit_time,std_fit_time,mean_score_time和std_score_time的单位均是秒。
print(clf.best_estimator_)# SVC(C=100000.0, gamma=0.01)print(clf.best_params_)# {'C': 100000.0, 'gamma': 0.01}print(clf.best_index_)# 2print(clf.best_score_)# 0.9500000000000001
不难看出,
clf.best_estimator_
等价于
SVC(**clf.best_params_)
,且最优参数
clf.best_params_
在列表
clf.cv_results_['params']
中的索引为 2,即
print(clf.cv_results_['params'][clf.best_index_]== clf.best_params_)# True
三、项目实战——鸢尾花分类
3.1 鸢尾花数据集介绍
sklearn 中有现成的鸢尾花数据集,我们可以从其中的
datasets
导入加载鸢尾花数据集的函数:
from sklearn.datasets import load_iris
鸢尾花数据集介绍:
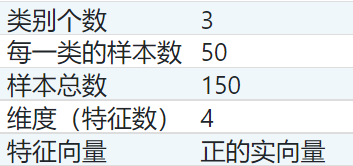
可以看出我们将面临的问题是一个多(三)分类问题。
3.2 sklearn.datasets.load_iris()
该函数最主要的参数只有一个:
return_X_y
。
r
e
t
u
r
n
_
X
_
y
:
\textcolor{blue}{\mathrm{return\_X\_y:}}
return_X_y:
默认值为
False
。
当值为
True
时,
load_iris()
将返回元组
(data, target)
(即
(X, y)
),否则将以
Bunch
对象(类字典对象)返回。
这里建议将
return_X_y
设置为
True
,这样我们就能很方便地使用两个参数进行接收:
X, y = load_iris(return_X_y=True)
如果设置为
False
(即默认状态),我们就只能:
iris = load_iris()
X, y = iris.data, iris.target
3.3 代码实现
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
param_grid ={'C':[1,1e1,1e2,1e3,1e4,1e5,1e6],'kernel':['rbf','linear'],'gamma':[1e-6,1e-5,1e-4,1e-3,1e-2,1e-1,1],}
clf = GridSearchCV(SVC(), param_grid, cv=5)
clf.fit(X_train, y_train)print(clf.best_params_)# {'C': 10.0, 'gamma': 0.1, 'kernel': 'rbf'}print(clf.score(X_test, y_test))# 0.9777777777777777
使用五折交叉验证,我们的最优参数为
(
C
=
10
,
γ
=
0.1
)
(C=10, \gamma=0.1)
(C=10,γ=0.1),且核为高斯核,最终模型在测试集上的分类准确率为
97.8
%
97.8\%
97.8%。
References
[1] Cross-validation: evaluating estimator performance.
[2] Tuning the hyper-parameters of an estimator.
[3] sklearn.datasets.load_iris.
[4] 机器学习. 周志华
版权归原作者 serity 所有, 如有侵权,请联系我们删除。