1、下面哪个不属于数据的属性类型( 相异 )
2、属于定量的属性类型是( 区间 )
3、一所大学内的各年纪人数分别为:一年级200人,二年级160人,三年级130人,四年级110人。则年级属性的众数是( 一年级 )
4、考虑数据集{12 24 33 24 55 68 26},其四分位数极差是( 31 )
5、光年所属的属性类型为( 比率标度属性 )
6、军衔所属的属性类型为( 序数属性 )
7、计算p1(2,1,4,10)和p2(3,0,3,8)两个对象之间的曼哈顿距离( 5 )
8、用AM 和PM 表示的时间的属性类型是( 二元 )
9、某部门的月薪情况如下(单位:千元),30,33,48,50,53,53,57,60,64,68,70,70,90,则该部门员工的月薪的均值为( 57.38 )千元(结果保留两位小数)
10、数据集{5,10,11,13,15,15,35,50,55,72,92,204,215}的中位数为( 35 ),众数为( 15 )
11、人的血型属于标称属性。( 对 )
12、离散属性总是具有有限个值。( 错 )
13、标称属性的值提供了足够的信息用于区分对象。( 对 )
14、二元属性的相异性有两种,一种是对称的二元相异性,另一种是非对称的二元相异性。( 对 )
15、已知点X的空间坐标为(3,4,2),点Y的空间坐标为(1,6,1),则X与Y的欧几里得距离为3。( 对 )
16、只有非零值才重要的二元属性被称作非对称二元属性。( 对 )
17、中心趋势度量包括均值、众数、中位数和中列数。( 对 )
18、已知点A的空间坐标为(6,30,9),点B的空间坐标为(10,35,2),则A与B之间的切比雪夫距离为7。( 对 )
19、属性可以分为标称属性、二元属性、序数属性和数值属性四类。( 对 )
20、假设给定的数据集的值已经分组为区间。区间和对应的频率如下。 则数据的近似分组中位数是( 32.94 )(结果保留两位小数)
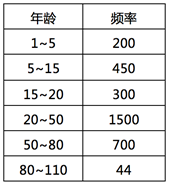
21、假设小明某一学期的考试成绩及每门课的学分如下表所示,则小明本学期的加权平均成绩为( 81.45 )(结果保留两位小数)

22、给定两个对象的元组x=(4,3,5,1)与y=(1,6,7,3),它们之间的余弦相似度为( 0.86 )(结果保留两位小数)
23、小明参加数学竞赛选拔赛,他十次测试成绩为:76,84,90,86,81,87,86,82,85,83。则小明同学十次测试成绩的方差是( 13.2 )(结果保留两位小数)
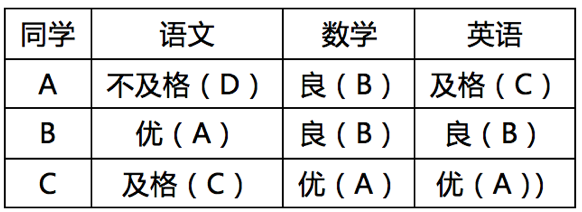
24、某组同学的成绩评定结果如下, 则A与B,A与C,B与C之间的相异性是( 1.05 )、( 0.82 )和( 0.82 )(结果均保留两位小数)
25、某部门的月薪情况如下(单位:千元),30,33,48,50,53,53,57,60,64,68,70,70,90,则该部门员工的月薪的均值为( 57.38 )千元(结果保留两位小数)
26、酒店的星级属于数值属性。( 错 )
27、某品种玉米苗中抽取10株,测得它们的株高为:21,42,39,14,19,22,37,41,40,25(单位:cm),则玉米苗株高的标准差为10.21。( 对 )
28、数值属性的值提供足够的信息确定对象的顺序。( 错 )
29、欧几里得距离、曼哈顿距离、闵可夫斯基距离和切比雪夫距离均满足非负性、同一性和三角不等式。( 对 )
30、余弦相似性利用向量空间中两个向量夹角的余弦值来衡量两个个体间的差异。余弦值越接近0,夹角越大,向量之间匹配越大。余弦值越接近1,夹角越小,向量之间匹配越小。( 错 )
31、计算由不对称的二元变量描述的对象间的相异度可以使用 Jaccard 系数;计算用分类变量描述的对象间的相异度可以采用属性值匹配的方法(属性值匹配,相似度为1,否则为0)。( 对 )
32、给定两个词向量元祖A(6,2,5,8)和B(4,5,2,6),则这两个对象之间的闵可夫斯基距离(其中h=4)是3.73。(结果保留两位小数)。( 对 )
33、假定用于分析的数据包含属性age,数据元组中age 的值如下(按递增序):13,15,16,16,19,20,20,21,22,22,25,25,25,25,30,33,33,35,35,35,35,36,40,45,45,52,70。则该组数据的中列数是41.5。( 对 )
版权归原作者 飞鸟与禅 所有, 如有侵权,请联系我们删除。