
在本文中,我们将看到几种基本的优化算法,可以用于各种数据科学问题。
机器学习中使用的许多算法都是基于基本的数学优化方法。由于各种先决条件,在机器学习的背景下直接看到这些算法,我们难免会感到困惑。因此,我认为最好不要在任何背景下查看这些算法,以便更好地理解这些方法。
下降算法
下降算法旨在最小化给定函数。你没有看错,就是这样。这些算法是迭代进行的,这意味着它们会不断改进当前的结果。你可能会想:
如果我想找到一个函数的最大值,怎么办?
很简单,只需在函数前面添加一个减号,它就会成为一个“最小”问题。
让我们继续。这是我们的问题定义:
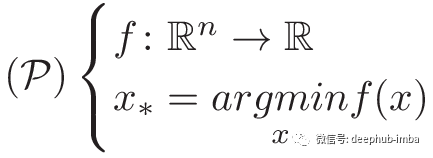
(我们的问题是找到一个向量x*,该向量能使函数f最小化)
你必须知道的一个先决条件是,如果一个点是极小点、极大点或鞍点,则函数在该点处梯度为零。
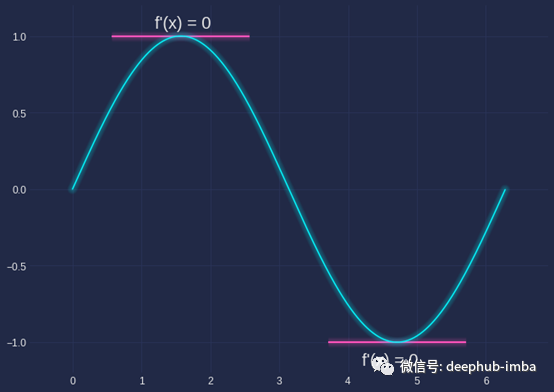
一维情况
下降算法包括构建一个向x* (arg min f(x))收敛的序列{x},序列的构建方法如下:
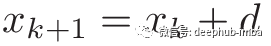
其中k是迭代次数,d是一个与{x}数量相同的向量,称为下降向量。
算法大致是这样的:
x = x_initwhile||gradient(f(x))|| < epsilon:x = x + d
我们一直对x进行更新,直到该点梯度的值足够小(在某个极值处应该达到零值)。
我们将看到3个不同的下降矢量(或方向矢量): 牛顿方向,梯度方向和渐变+最佳步长方向。首先,我们需要定义一个供测试用的函数。
Rosenbrock函数
我选择了Rosenbrock函数,但你可能会发现很多其他类似的测试函数。Himmelblau函数也是一个不错的选择。
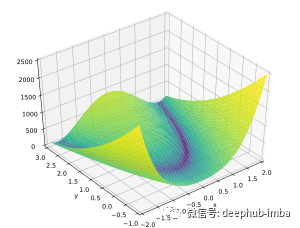
Rosenbrock函数-维基百科
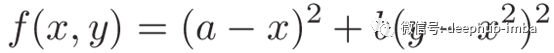
它的全局最小值为(x, y)=(a, a²),其中f(a, a²) =0,通常取a=1,b=100。
我们还需要另外两条信息,即该函数的梯度以及hessian矩阵。
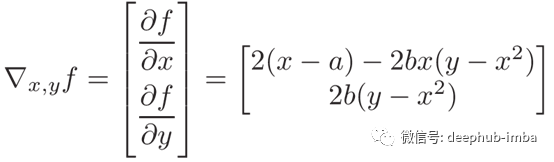
Rosenbrock函数的梯度
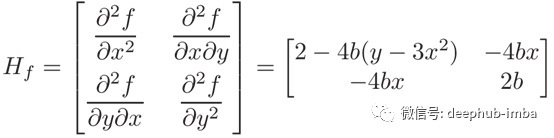
Rosenbrock函数的Heiian矩阵
让我们打开一个文件并启动Python脚本。
这是我们的第一段代码:
import numpy as np
defrosenbrock(X, a=1, b=100): x, y = Xreturn (a - x)**2 + b * (y - x**2)**2
defrosenbrock_grad(X, a=1, b=100): x, y = Xreturn np.array([2 * (x - a) - 4 * b * x * (y - x**2),2 * b * (y - x**2) ])
defrosenbrock_hess(X, a=1, b=100): x, y = Xreturn np.matrix([ [2 - 4 * b * (y - 3 * x**2), -4 * b * x], [-4 * b * x, 2 * b] ])
类似于之前的定义,现在我将把函数输入向量称为x。现在我们已经准备好了,让我们看看第一个下降向量!
Newton方向
Newton方向如下:
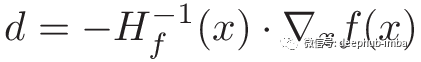
每一次的更新为:
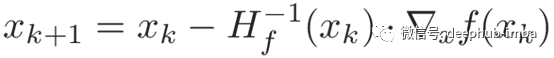
你可以取f(x + d)二阶泰勒展开式来找到更新后的公式。
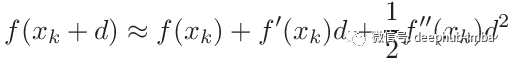
我们希望找到使f(x + d)尽可能小的d。如果f’’(x)为正,则该方程是一个具有最小值的抛物线。当f(x + d)的一阶导数为零时,函数达到最小值。
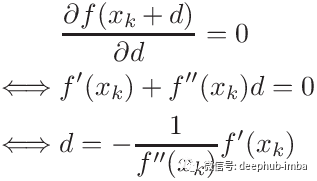
而在n维中,f’’(x)为hessian矩阵,1/f’’(x)为逆hessian矩阵。最后,f’(x)为梯度。
我们需要计算hessian矩阵的逆。对于大型矩阵,这是一项计算量很大的任务。因此,实际上,我们以完全等效的方式解决了这一问题。
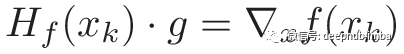
我们解出关于g的这个方程式,而不是计算hessian矩阵的逆,并使更新规则如下:
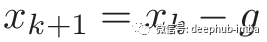
现在让我们用代码实现算法:
defnewton(J_grad, J_hess, x_init, epsilon=1e-10, max_iterations=1000): x = x_initfor i in range(max_iterations): x = x - np.linalg.solve(J_hess(x), J_grad(x))if np.linalg.norm(J_grad(x)) < epsilon:return x, i + 1return x, max_iterations
你会发现与我在开始时介绍的算法略有不同。我添加了一个max_ iteration参数,以便该算法在不收敛时不会永远运行下去。
Let’stry it!
# Rosenbrock has 2 input variables, I set them to zero at firstx_init = np.zeros(2)x_min, it = newton(rosenbrock_grad, rosenbrock_hess, x_init)print('x* =', x_min)print('Rosenbrock(x*) =', rosenbrock(x_min))print('Grad Rosenbrock(x*) =', rosenbrock_grad(x_min))print('Iterations =', it)
我们得到以下结果:
x* = [1. 1.]Rosenbrock(x*) = 0.0Grad Rosenbrock(x*) = [0. 0.]Iterations = 2
我们看到,该算法仅需2次迭代即可达到收敛!这真的很快。您可能会认为:
嘿,初始x非常接近目标x,这使任务变得很容易! *
你是对的!我们尝试其他一些初始值,例如x_ init= [50,-30],该算法经过5次迭代终止。
此算法称为牛顿法,所有下降算法都是该方法的修改,都以该算法为母体。它真正快速的原因是它使用了二阶信息(hessian矩阵)。
即使使用了hessian,即使使用hessian矩阵也要付出代价:效率。计算逆矩阵是一项计算量很大的任务,因此数学家想出了解决此问题的解决方案。
主要是:拟牛顿法和梯度法。拟牛顿法尝试使用各种技术来逼近hessian 矩阵的逆,而梯度法只使用一阶信息。
梯度方向
如果你学过一些机器学习,你可能已经看到梯度方向为:
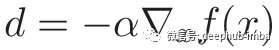
其中,α称为步长(或ML中的学习率),是范围[0,1]内的实数。
如果你一直在做一些机器学习相关的事情,你可能知道这个公式实际上是一个更大的公式的一部分:牛顿方向,我们用常数代替了逆hessian矩阵。Anyway,更新规则变为:
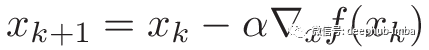
算法变为:
defgradient_descent(J_grad, x_init, alpha=0.01, epsilon=1e-10, max_iterations=1000): x = x_initfor i in range(max_iterations): x = x - alpha * J_grad(x)if np.linalg.norm(J_grad(x)) < epsilon:return x, i + 1return x, max_iterations
让我们尝试一下:
x_init = np.zeros(2)x_min, it = gradient_descent(rosenbrock_grad, x_init, alpha=0.002, max_iterations=5000)print('x* =', x_min)print('Rosenbrock(x*) =', rosenbrock(x_min))print('Grad Rosenbrock(x*) =', rosenbrock_grad(x_min))print('Iterations =', it)
你可以调整alpha, epsilon和max_ iterations的值。我们得到类似于牛顿法的结果:
x* = [0.99440769 0.98882419]Rosenbrock(x*) = 3.132439308613923e-05Grad Rosenbrock(x*) = [-0.00225342 -0.00449072]Iterations = 5000
与牛顿算法相比,该算法收敛速度如此之慢的主要原因是,我们不仅不再使用的二阶导数所给出的信息,而且还使用常数来代替逆hessian矩阵。Wow!梯度下降法进行了5000次迭代,而牛顿法仅进行了2次!另外,该算法还没有完全达到最小点(1,1)。
想一想。函数的导数是该函数的变化率。因此,hessian给出了有关梯度变化率的信息。由于找到最小值必然意味着该点梯度为零,而hessian告诉了你梯度何时升高或降低,因此变得非常有用。
机器学习中的许多论文都只是为这一特定步骤寻找更好的方法。比如:Momentum,Adagrad或Adadelta。
梯度方向和最佳步长
对经典梯度下降法的一种改进是:在每次迭代中使用可变步长,而不是常数。它不仅是可变的步长,而且最好还是最佳步长。
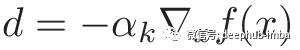
αk为每次迭代的步长
每次迭代更新为:
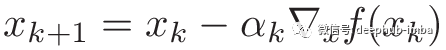
我们如何找到α?由于我们希望此更新尽可能高效,即使得f最小化,也就是说我们正在寻找α,使得:
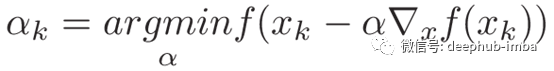
请注意,在此步骤中,x和grad(x)是常量。因此,我们可以定义一个新函数q:
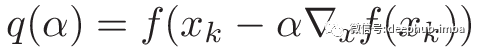
其中q实际上是一个单一变量函数。我们想找到使该函数最小化的α。emmm..梯度下降?是的,但是当我们这样做时,让我们先学习一种新方法:Golden Section Search。
Golden SectionSearch旨在查找指定间隔内函数的极值(极大或极小)。由于我们使用的α的范围为[0,1],因此这是使用此算法的绝佳机会。
由于这篇文章从开始到现在已经很长了,我不再赘述。
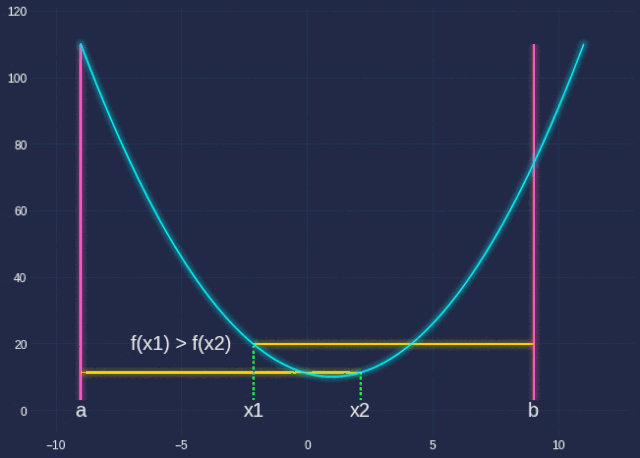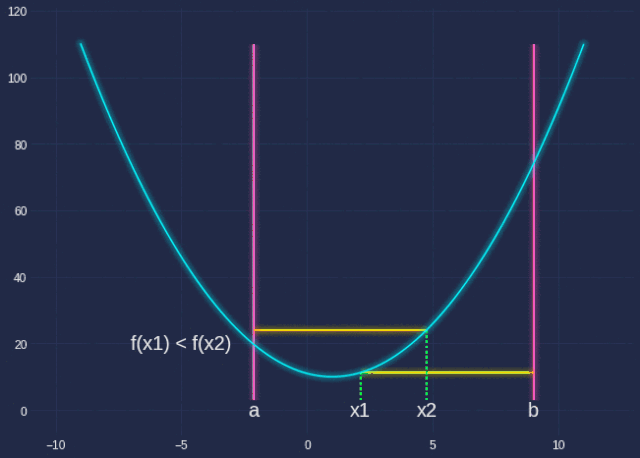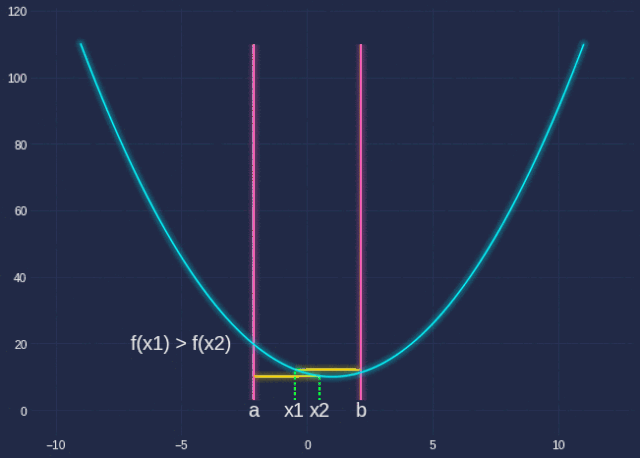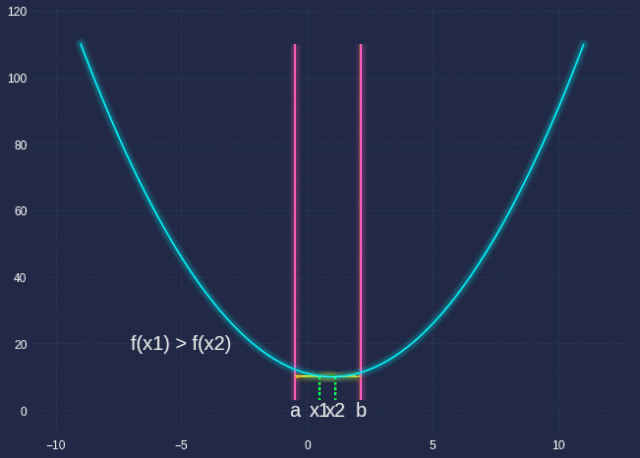
希望借助我花了很长时间才制作的GIF,以及下面的代码,你能够了解这里发生的事情。
# https://en.wikipedia.org/wiki/Golden-section_search#Algorithmdefgss(f, a, b, tol=1e-7):phi = (np.sqrt(5) + 1) / 2d = b - (b - a) / phic = a + (b - a) / phi
whileabs(d - c) > tol:iff(d) < f(c):b = celse:a = d
d = b - (b - a) / phic = a + (b - a) / phi
return(a + b) / 2
现在我们能够找到最佳的α,下面我们用最佳步长编写梯度下降代码!
defgradient_descent_optimal(J, J_grad, x_init, epsilon=1e-10, max_iterations=1000):x = x_initfori in range(max_iterations):q = lambda alpha: J(x - alpha * J_grad(x))alpha = gss(q, 0, 1)x = x - alpha * J_grad(x)ifnp.linalg.norm(J_grad(x)) < epsilon:returnx, i + 1returnx, max_iterations
然后,我们运行代码:
x_init = np.zeros(2)x_min, it = gradient_descent_optimal(rosenbrock, rosenbrock_grad, x_init, max_iterations=3000)print('x* =', x_min)print('Rosenbrock(x*) =', rosenbrock(x_min))print('Grad Rosenbrock(x*) =', rosenbrock_grad(x_min))print('Iterations =', it)
得到以下结果: .
x* = [0.99438271 0.98879563]Rosenbrock(x*) = 3.155407544747055e-05Grad Rosenbrock(x*) = [-0.01069628 -0.00027067]Iterations = 3000
Conclusion
即便在这种情况下,我们结果并不明显好于纯梯度下降,但通常来说,最佳步长效果更好。例如,我尝试用Himmelblau函数进行相同的比较,有最佳步长的梯度下降速度是纯梯度下降速度的两倍以上。
到此为止。希望您学到的这些新东西了能够激发出您对数学优化的好奇心!还有许多其他有趣的方法,去找他们吧!
别忘了看看GoogleColab文件,您会找到所有使用的代码以及我们对Himmelblau函数所做的相同测试。
作者:Omar Aflak
本文代码:https://colab.research.google.com/drive/1jOK_C_pSDV6J98ggV1-uEaWUrPuVm5tu
Deephub翻译组:张森豪
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
好看就点在看!********** **********