文章目录
前言
入门机器学习分类问题,总有些内容是绕不过的,为了辨别模型好坏,必须要了解模型评估的各项指标。
为了能够加深记忆,本人在基于他人文章的基础下写了本篇博客,同时也方便自身查阅。
看懂机器学习指标:准确率、精准率、召回率、F1、ROC曲线、AUC曲线
什么是ROC曲线?为什么要使用ROC?以及 AUC的计算
一、混淆矩阵(confusion matrix)
二分类的在此不作介绍,此图为我最近训练的比较差的四分类模型(yolo5s-v6)所生成的混淆矩阵: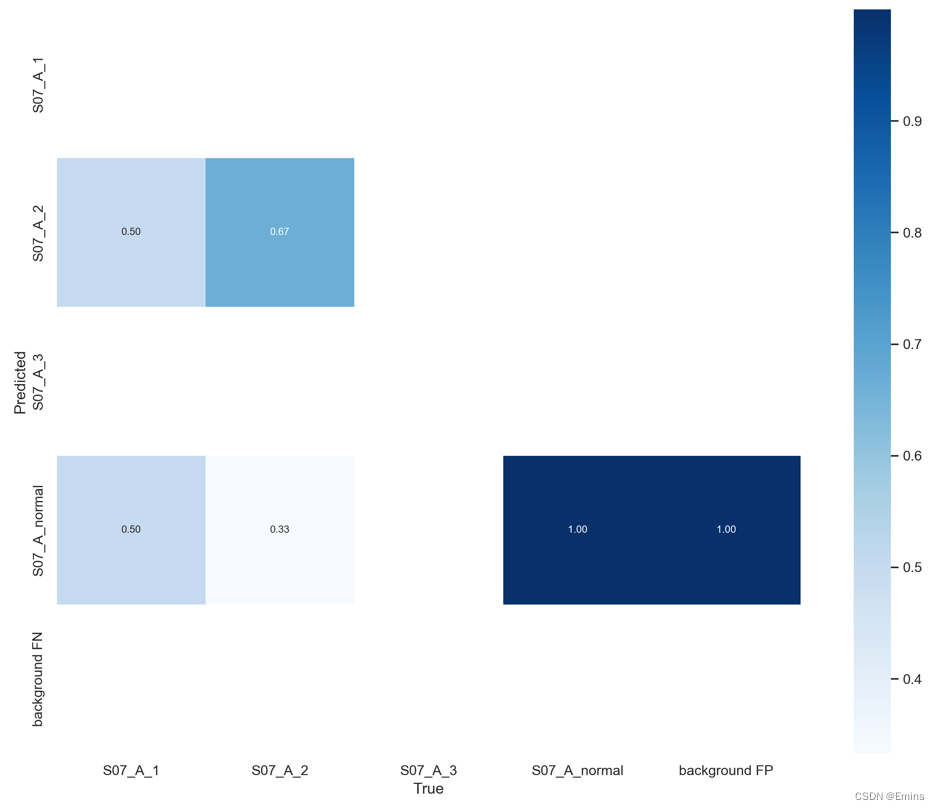
具体解释如下:
X横坐标为正确的分类(即你用标签所标注的真实分类)
Y纵坐标为模型所预测的分类(即图片经过模型推理后模型将其辨别为的分类)
举例,如S07_A_1:
该项分类的训练结果很差,有50%被认为是S07_A_2,另外50%则是S07_A_normal,也就是模型完全无法分辨出S07_A_1这项分类。
举例,如S07_A_3:
该项没有训练到任何分类数据,所以指标上一片空白。
还有 background FP和 background FN会比较难解释些:
这里先普及一下多分类下的TN、TP、FN、FP的概念:
True positives (TP): 缺陷的图片被正确识别成了缺陷。(本缺陷的正确分类预测)
True negatives(TN): 背景的图片被正确识别为背景。(非本缺陷被预测为其他分类缺陷或背景)
False positives(FP): 背景的图片被错误识别为缺陷。(非本缺陷被预测为本缺陷)
False negatives(FN): 缺陷的图片被错误识别为背景。(本缺陷被预测为其他缺陷或者背景)
举例,如background FP(背景的图片被错误识别为缺陷):
100%在S07_A_normal的横坐标上,即100%的背景都被认为是S07_A_normal缺陷。
如background FN(缺陷的图片被错误识别为背景):
一片空白,即没有任何的缺陷被误判为背景。
这里我引进之前做的一个单分类模型:

这是一个只判断是否为鱼的模型,即打标签时只有一个分类:
可以看出,有22%的鱼被模型认为是背景(background FN),不过模型并没有将任何背景认为是鱼(background FP)。
清楚了TP、TN、FP、FN的各项概念,就可以去计算各项分类的其余指标了。
二、准确率,精准率,召回率,F1分数
这里当然也是不对二分类做论述,同样举例刚刚的四分类模型:
同时拟定了他们的分类个数:
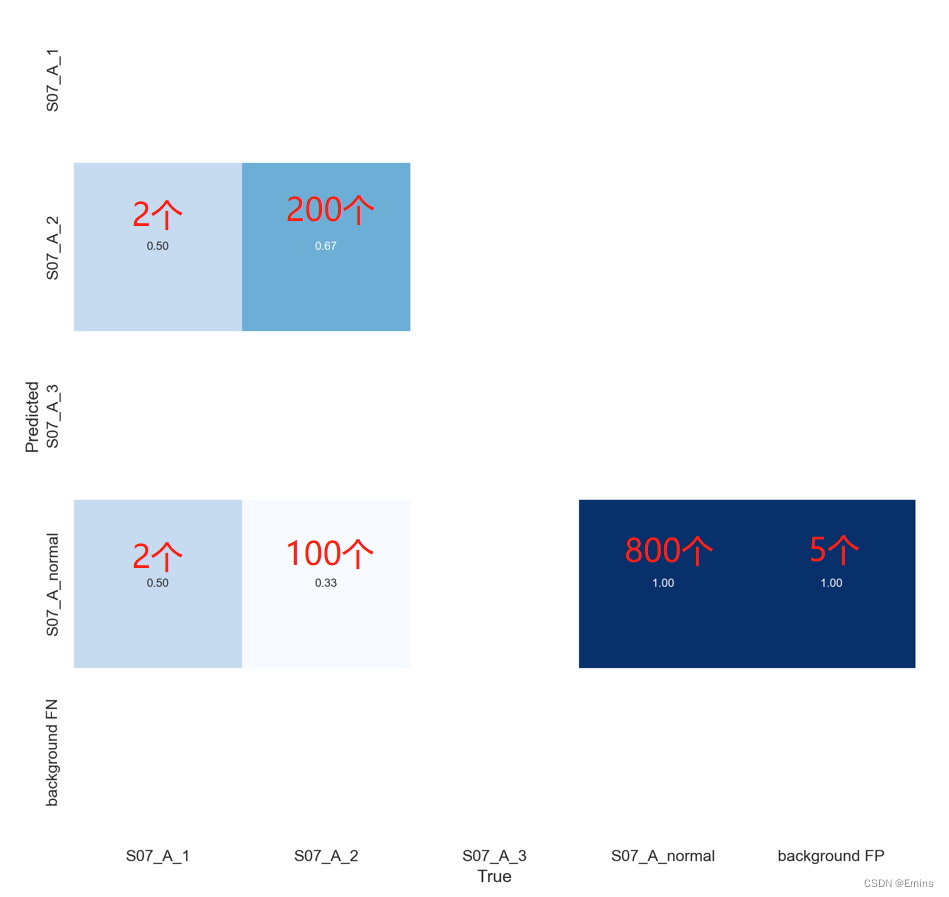
实际上background FP的数量很少,大多数是没有标记的S07_A_normal,一般寥寥几个,假设为5个。
1. 准确率(Accuracy)
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
F
P
+
T
N
+
F
N
Accuracy = \frac{TP+TN}{TP+FP+TN+FN}
Accuracy=TP+FP+TN+FNTP+TN
即
本缺陷的正确分类预测
加上
非本缺陷被预测为其他分类缺陷或背景
除以总预测数量。
在正负样本数量接近的情况下,准确率越高,模型的性能越好,例如S07_A_normal:
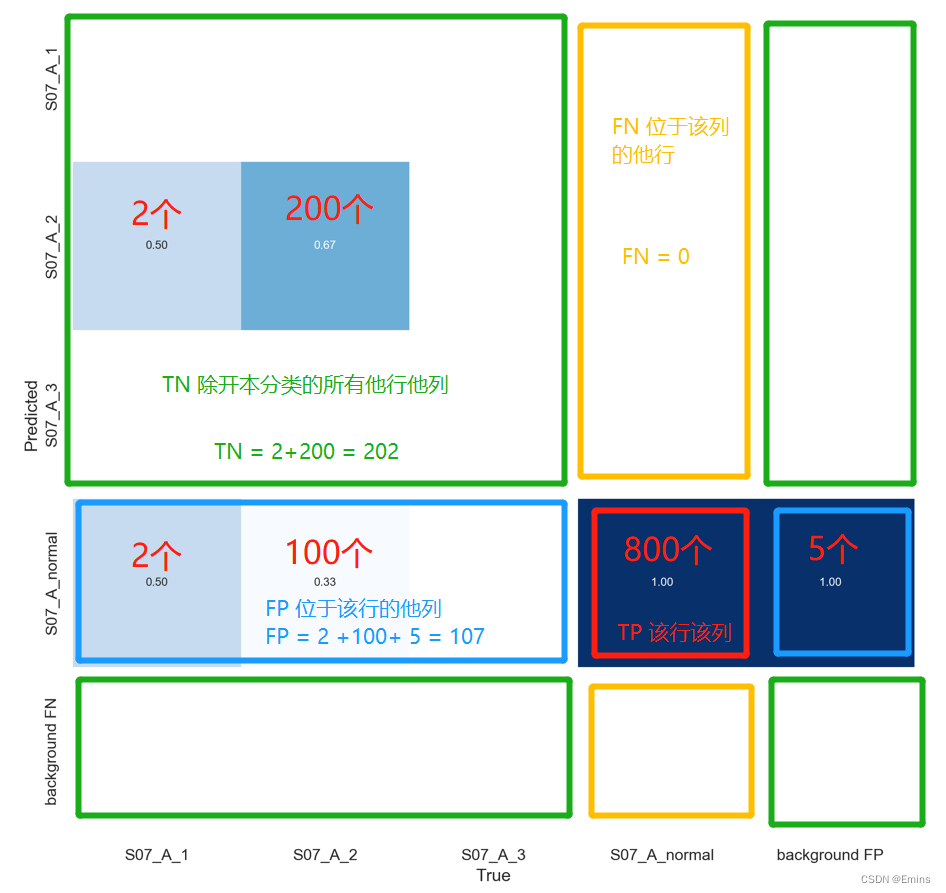
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
F
P
+
T
N
+
F
N
=
800
+
(
200
+
2
)
800
+
(
5
+
100
+
2
)
+
(
200
+
2
)
+
0
=
90.35
%
Accuracy = \frac{TP+TN}{TP+FP+TN+FN} = \frac{800+(200+2)}{800+(5+100+2)+(200+2)+0} = 90.35\%
Accuracy=TP+FP+TN+FNTP+TN=800+(5+100+2)+(200+2)+0800+(200+2)=90.35%
不过由于准确率的局域性,在TP和TN相差太大的情况下,例如S07_A_1:
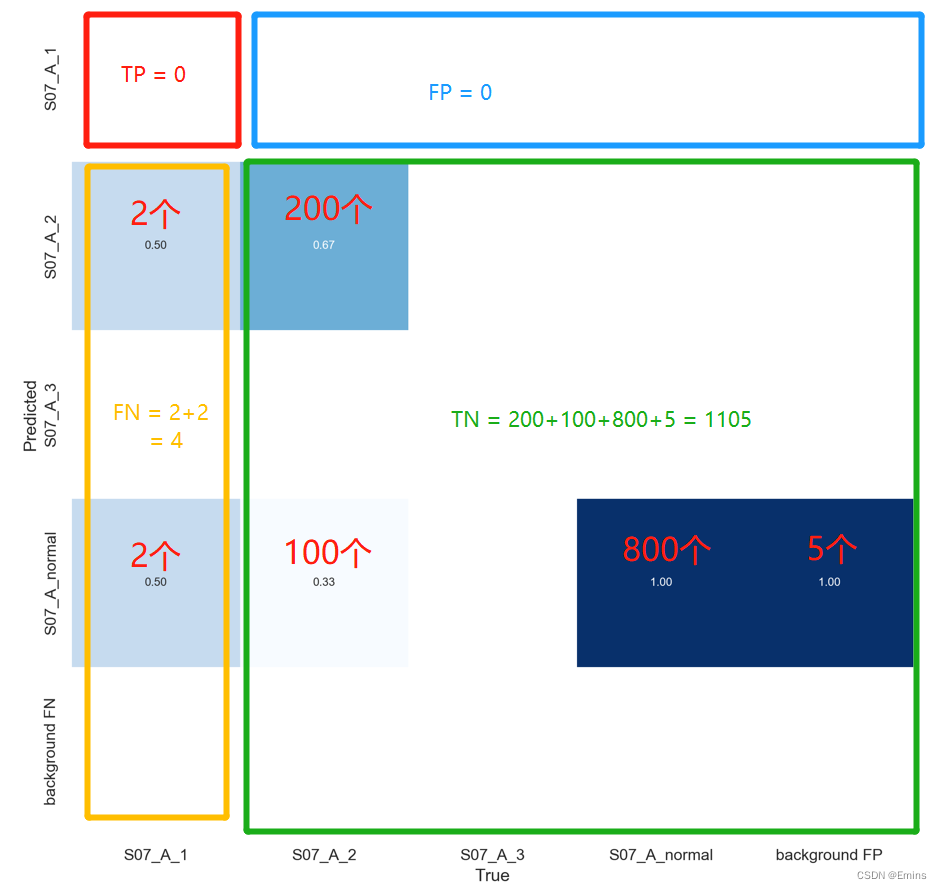
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
F
P
+
T
N
+
F
N
=
0
+
(
200
+
100
+
5
+
800
)
0
+
0
+
(
200
+
100
+
5
+
800
)
+
(
2
+
2
)
=
99.64
%
Accuracy = \frac{TP+TN}{TP+FP+TN+FN} = \frac{0+(200+100+5+800)}{0+0+(200+100+5+800)+(2+2)} = 99.64\%
Accuracy=TP+FP+TN+FNTP+TN=0+0+(200+100+5+800)+(2+2)0+(200+100+5+800)=99.64%
可见,S07_A_1的识别率这么差,但是计算的Accuracy还这么高,因此,不能仅仅从单项准确率来判断模型的好坏。
总体准确率: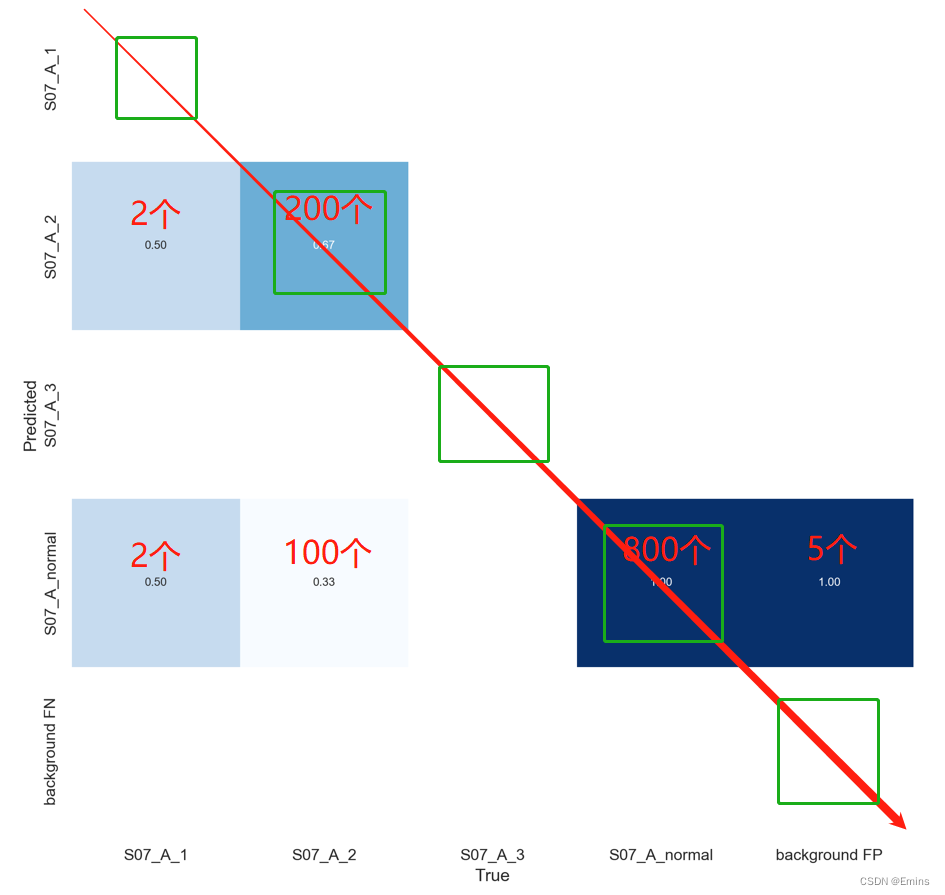
A
c
c
u
r
a
c
y
=
正
方
形
k
=
−
1
的
对
角
线
值
所
有
样
本
数
=
0
+
200
+
0
+
800
+
0
)
2
+
200
+
2
+
100
+
800
+
5
=
90.17
%
Accuracy = \frac{正方形k=-1的对角线值}{所有样本数} = \frac{0+200+0+800+0)}{2+200+2+100+800+5} = 90.17\%
Accuracy=所有样本数正方形k=−1的对角线值=2+200+2+100+800+50+200+0+800+0)=90.17%
若是以Accuracy来说模型质量很好,不过这都归功于庞大的S07_A_normal数据及其高正确率,其他分类识别率很差。
2. 精确率(Precision)
精准率(Precision)又叫查准率,它是针对
预测结果
而言的,它的含义是`在所有被预测为正的样本中实际为正的样本的概率``,意思就是在预测为正样本的结果中,我们有多少把握可以预测正确,其公式如下:
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision = \frac{TP}{TP+FP}
Precision=TP+FPTP
也就是只看分类所在行,对于S07_A_normal来说:
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
=
800
800
+
(
2
+
100
+
5
)
=
88.20
%
Precision = \frac{TP}{TP+FP} = \frac{800}{800+ (2+100+5)} = 88.20\%
Precision=TP+FPTP=800+(2+100+5)800=88.20%
结果来说,略低于准确率的90.35%
对于S07_A_01来说:
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
=
0
0
+
0
=
?
%
Precision = \frac{TP}{TP+FP} = \frac{0}{0+0} = ?\%
Precision=TP+FPTP=0+00=?%
没有结果预测成为S07_A_01,已经可以看出来是一个失败的分类。
3. 召回率(Recall)
召回率(Recall)又叫
查全率
,它是针对
原样本
而言的,它的含义是
在实际为正的样本中被预测为正样本的概率
,其公式如下:
R
e
c
a
l
l
=
T
P
T
P
+
F
N
Recall = \frac{TP}{TP+FN}
Recall=TP+FNTP
也就是只看分类所在列,对于S07_A_normal来说:
R
e
c
a
l
l
=
T
P
T
P
+
F
N
=
800
800
+
0
=
100.00
%
Recall = \frac{TP}{TP+FN} = \frac{800}{800+ 0} = 100.00\%
Recall=TP+FNTP=800+0800=100.00%
所有的S07_A_normal都被识别出来,很成功。
对于S07_A_normal来说:
R
e
c
a
l
l
=
T
P
T
P
+
F
N
=
0
0
+
(
2
+
2
)
=
0.00
%
Recall = \frac{TP}{TP+FN} = \frac{0}{0+ (2+2)} = 0.00\%
Recall=TP+FNTP=0+(2+2)0=0.00%
所有的S07_A_01都没被识别出来,很失败。
对比高达99.64%的准确率,召回率更能反映S07_A_01的实际性能。
4. F1分数
1. 概念
通过上面的公式,我们发现:精准率和召回率的分子是相同,都是TP,但分母是不同的,一个是(TP+FP),一个是(TP+FN)。两者的关系可以用一个P-R图来展示:
F
1
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
F1 = \frac{2 \times Precision \times Recall}{Precision + Recall}
F1=Precision+Recall2×Precision×Recall
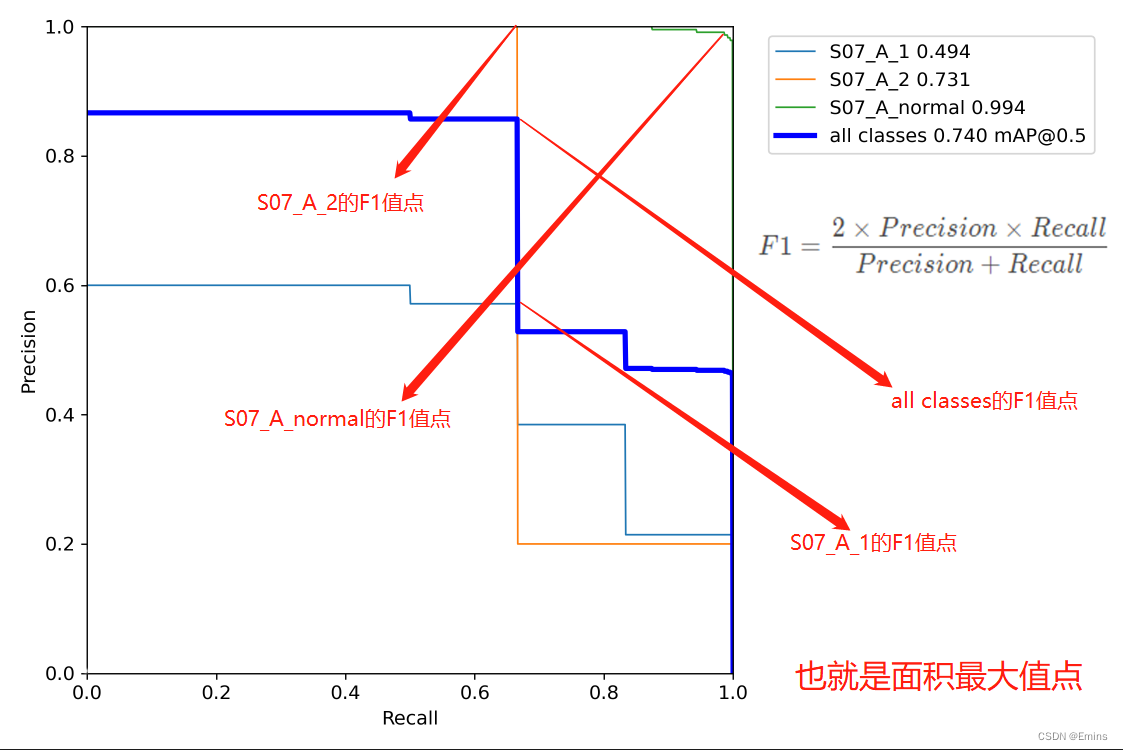
对于图中,
交点乘积最大值——面积最大值
即为该分类的F1值。
不过对于连续光滑的曲线,F1最大值点为 Precision=Recall 的直线与PR曲线的交点。
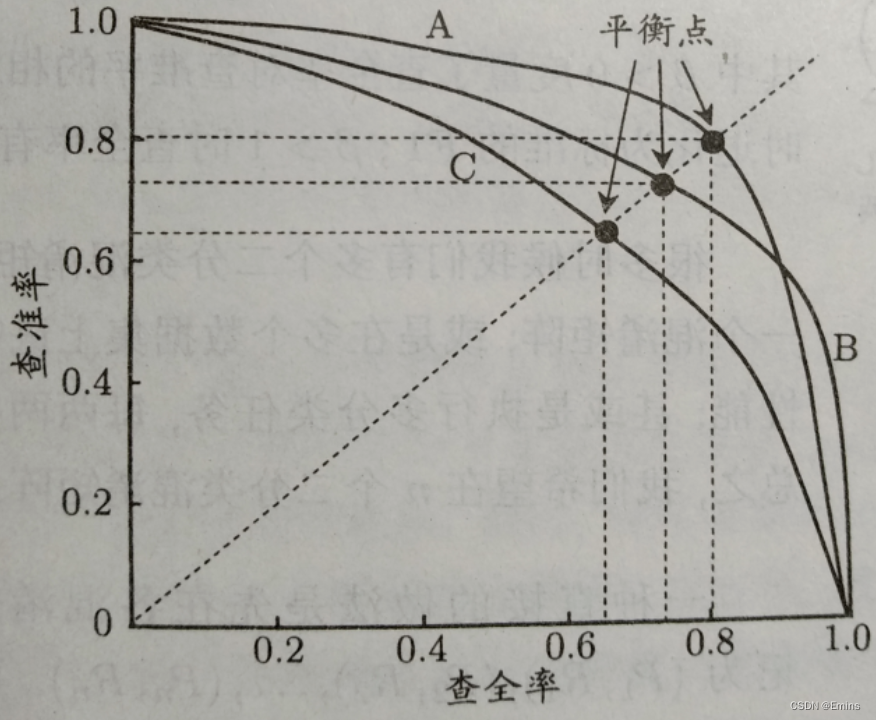
那么应该都很好奇,不是前面计算S07_A_1的Recall和Precision都是0%吗?为什么该处就有值了?
那先要引入一个概念:置信度(Confidence)
2. 置信度(Confidence)
在获取最优F1前,先理解置信度的设定。
置信度(Confidence)可以理解为阈值,如我之前设定50%以上就判断为真,现在设定10%以上就为真,那么:
TP、FP个数就加多
(模型会把更多该分类或不是该分类的标签认定为该分类)。
继而
TN、FN个数会减少
,因此Prediction和Recall都会因为置信度的改变而变化。
相反,如果我现在设定90%以上才为真,那么:
TP、FP个数就减少
(模型会把更多该分类或不是该分类的标签认定为其他该分类)
继而
TN、FN个数会增多
。
一般来说,
置信度设定越大,Prediction约接近1,Recall越接近0。
因此,要寻找
最优的F1分数,需要遍历置信度。
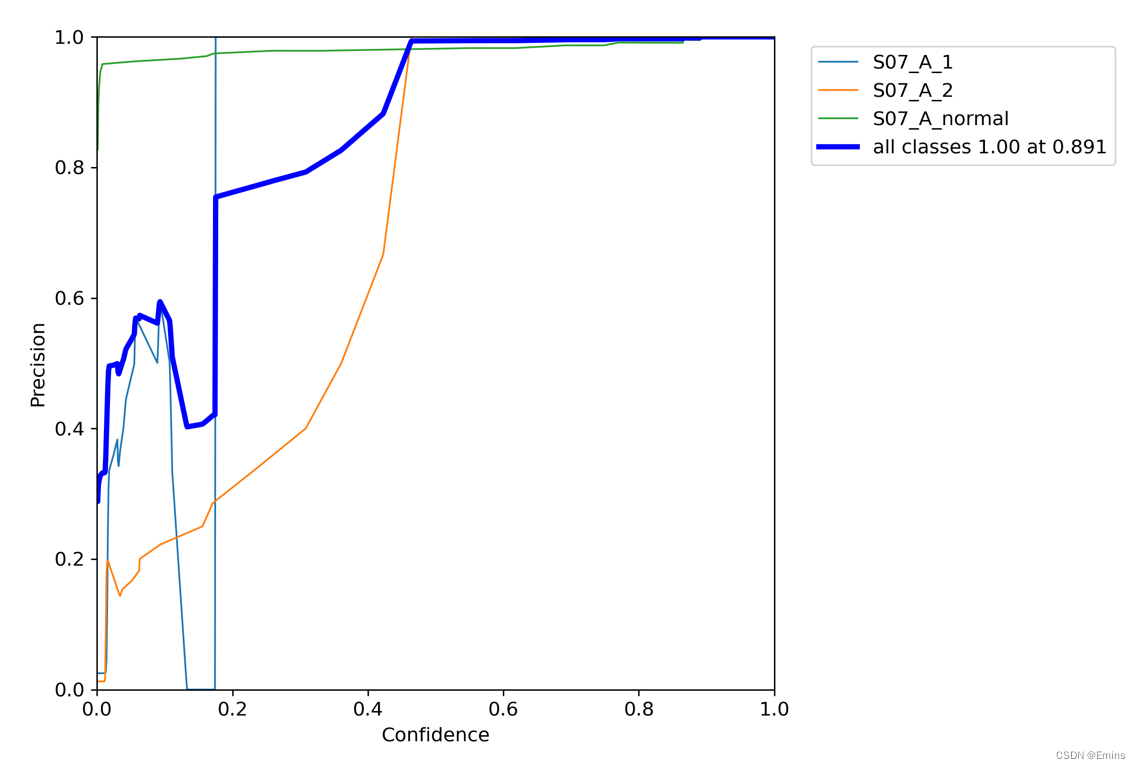
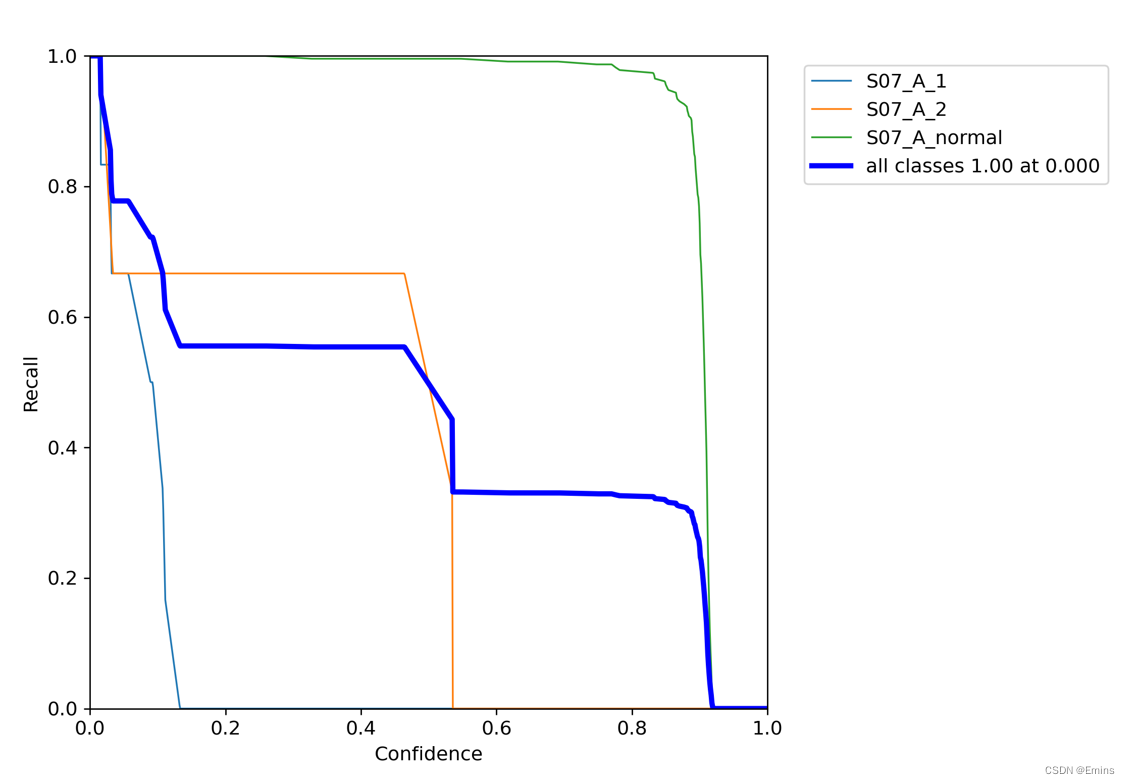
3. F1曲线图判断
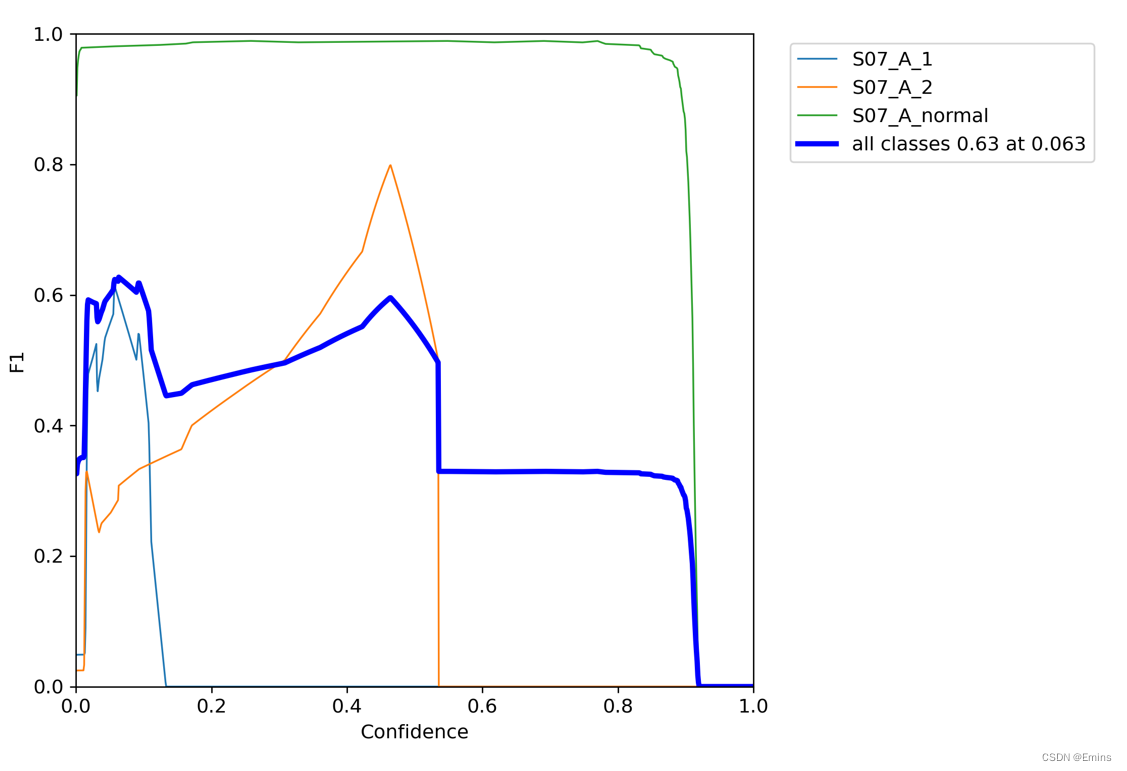
F1分数置于[0,1]间,越接近1是越好的,没有例外。
由上可以看出,在置信度为6.3%的情况下,模型整体的最高F1分数为0.63,并不是一个好的模型。
三、mAP、ROC、AUC
1. 总体平均精确度:mAP(mean Average Precision)
将recall设置为横坐标,precision设置为纵坐标。PR曲线下围成的面积即AP,所有类别AP平均值即mAP
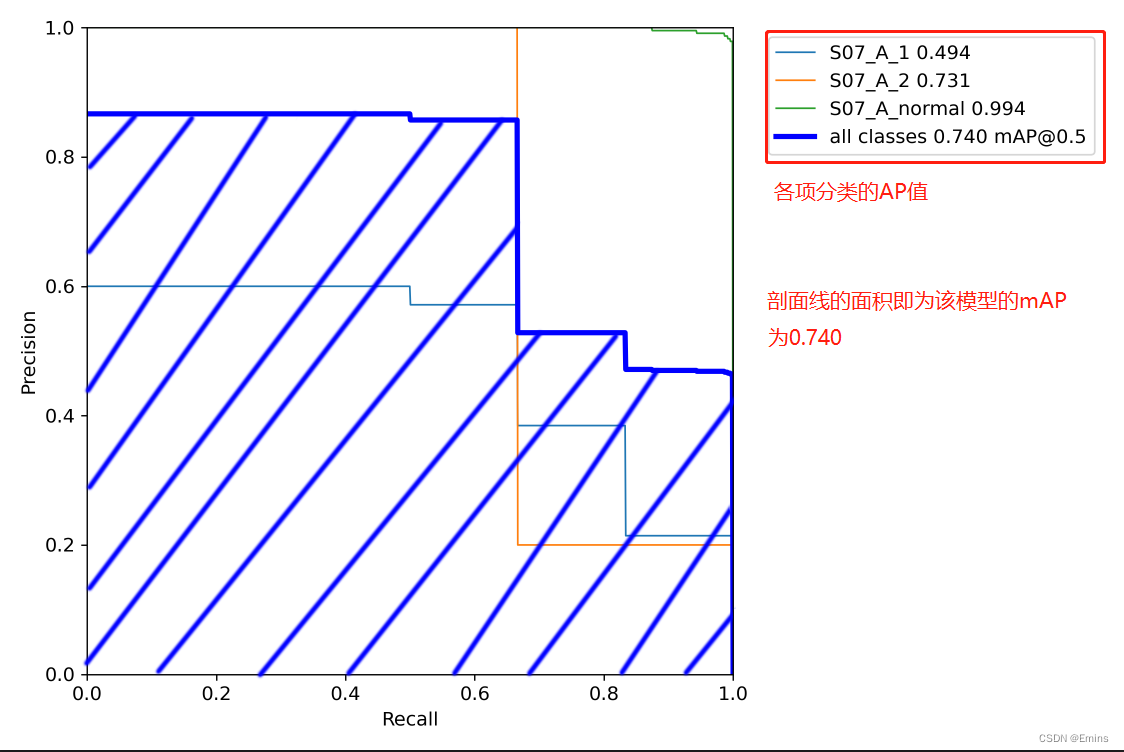
mAP值越接近1说明模型越优秀。
肯定多少有些疑惑,mAP@0.5后面的0.5代表什么含义。
这里就要再引入一个概念,重叠度:Intersection over Union(IoU)
重叠度:Intersection over Union(IoU)
IoU的全称为交并比(Intersection over Union),是目标检测中使用的一个概念,IoU计算的是“预测的边框”和“真实的边框”的交叠率,即它们的交集和并集的比值。最理想情况是完全重叠,即比值为1。
以下举个例子来简要说明:

因此IoU=0.5就是预测框和标注框的交集与非交集占比相同,都为50%。
显而易见的是,IoU受confidence置信度影响,因此,对于IoU和confidence的调参也是一个需要注意的事情。
2. ROC(Receiver Operating Characteristic)
ROC(Receiver Operating Characteristic)曲线,又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域,用于区分信号与噪声。后来人们将其用于评价模型的预测能力,ROC 曲线是基于混淆矩阵得出的。
类似于PR曲线一般,ROC是以FPR为横坐标,TPR为纵坐标所构建的曲线,因此在了解ROC前,首先先理解TPR和FPR。
设定以下模型:
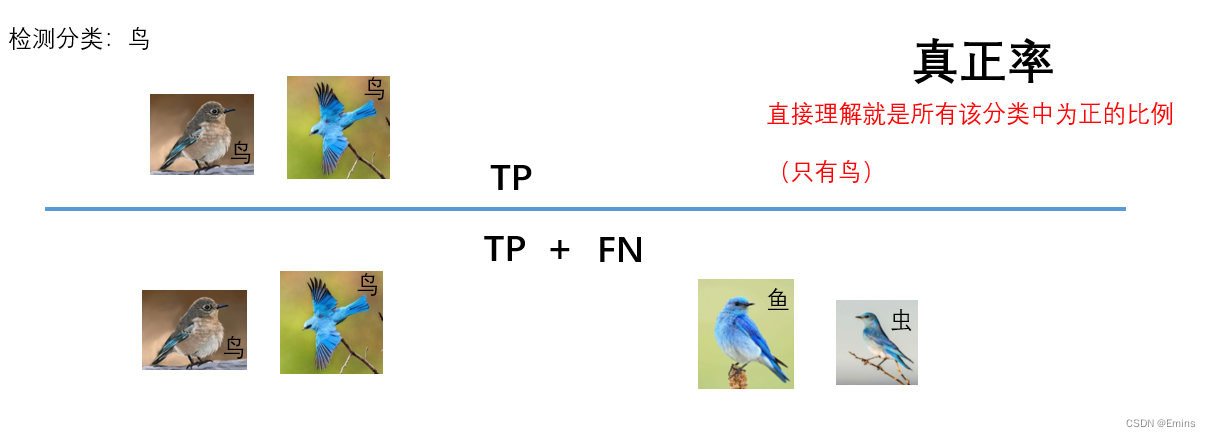
TPR真正率(Sensitivity、True Positive Rate)
T
P
R
=
T
P
T
P
+
F
N
TPR = \frac{TP}{TP + FN}
TPR=TP+FNTP
意为:
所有被预测为该分类的缺陷
中
真正属于该分类的缺陷
的比例。
举例:
FPR假正率(False Positive Rate)
F
P
R
=
F
P
F
P
+
T
N
FPR = \frac{FP}{FP + TN}
FPR=FP+TNFP
意为:
所有其他分类的缺陷
中
被认为是该分类的缺陷
的比例。
举例: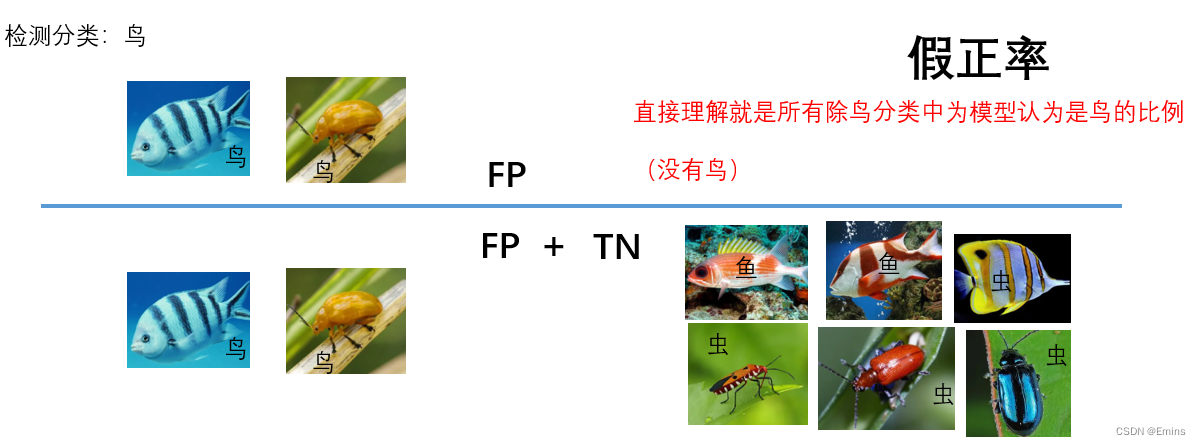
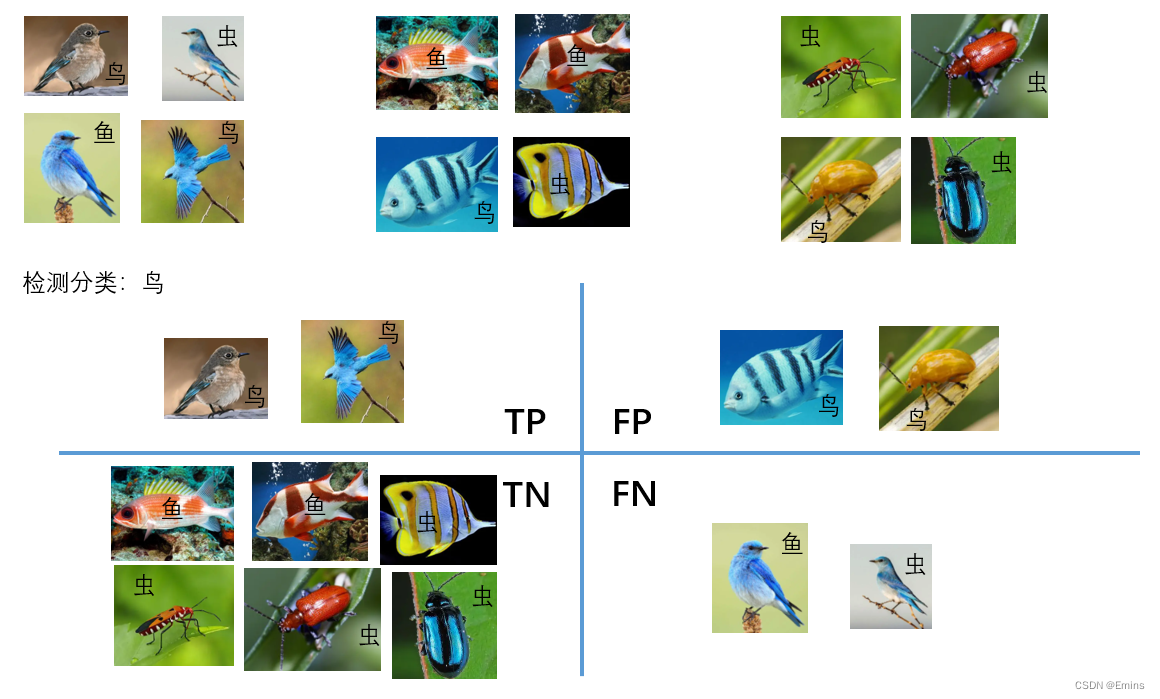
可以看出,真正率仅仅是对标注为鸟(
该分类——正样本
)的判断,假正率仅仅是对标注不为鸟(
非该分类的所有分类——负样本
)的判断。
也就是说,无论正样本和负样本的数量差距有多少,这两种比率仅会在其对应的正样本或者负样本中计算,没有交叉,因此可以
无视正负样本比例
,并不会像Accuary准确率那样受正负样本比例影响非常大。
(具体可以参考一下S07_A_1的准确率)
通过定义的解释,不难看出,想要模型更加优秀,假正率FPR越低越好,真正率TPR越高越好。
也就是:
TP↑、TN↑、FP↓、FN↓
因此,ROC曲线同PR曲线,一样受到置信度的影响,所以他也和PR曲线一样遍历置信度绘制:
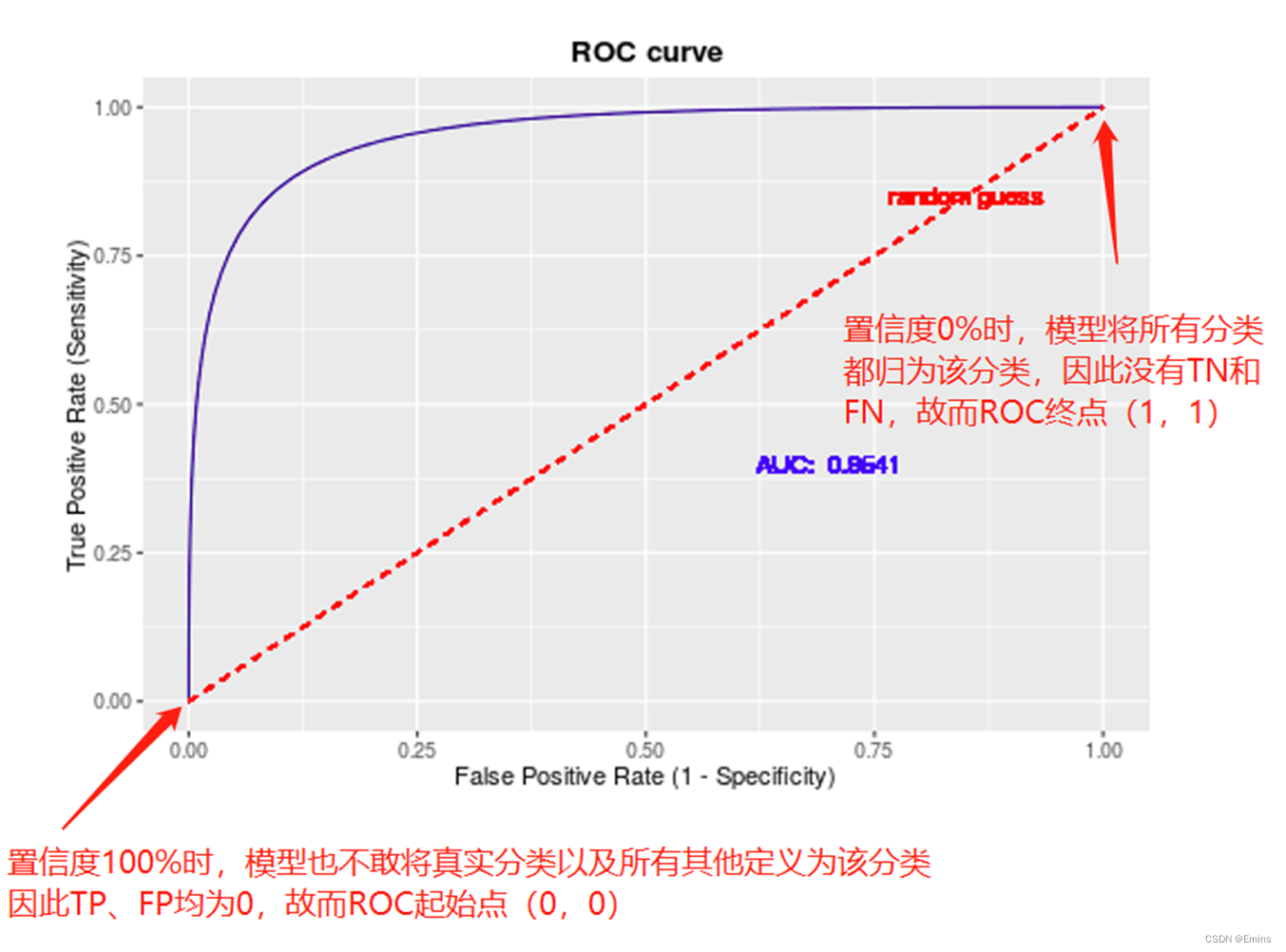
可以看出,对于ROC曲线,左上角最大值点越接近 [0,1] 越好,可以说曲线与 TPR = 0 和 FPR = 1的直线相交面积越大越好,这个面积称为AUC。
3. AUC(Area Under roc Curve)
先看我前言提到的这篇文章——什么是ROC曲线?为什么要使用ROC?以及 AUC的计算
这文章已经非常详细地介绍了ROC和AUC。
AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
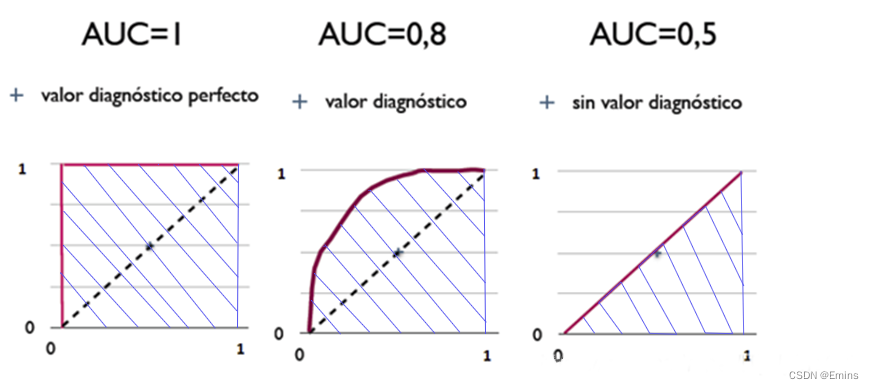
简单来说,AUC 的一般判断标准:
0.5 – 0.7: 效果较低,但用于预测股票已经很不错了
0.7 – 0.85: 效果一般
0.85 – 0.95: 效果很好
0.95 – 1: 效果非常好,但一般不太可能
(扩展:Yolov5 训练所生成的所有文件)
最后再给一个链接解释所有yolov5所生成的训练文件:
yolov5 训练结果解析
版权归原作者 Emins 所有, 如有侵权,请联系我们删除。