DRL基础（一）——强化学习发展历史简述

【摘要】介绍强化学习的起源、发展、主要流派、以及应用。强化学习理论和技术很早就被提出和研究了，属于人工智能三大流派中的行为主义。强化学习一度成为人工智能研究的主流，而最近十年多年随着以深度学习为基础的联结主义的兴起，强化学习与之结合后在感知和表达能力上得到了巨大提升，在解决某些领域的问题中达到或者超过了人类水平。在围棋领域，基于强化学习和蒙特卡洛树搜索的AlphaGo打败了世界顶级专业棋手；在视频游戏领域，基于深度强化学习的游戏智能体在29款Atari游戏中超过人类平均水平；在即时战略游戏领域，AlphaStar和OpenAI Five分别在星际争霸II和Dota 2这两款游戏中达到了顶尖人类玩家的水平；在德州扑克领域，一个叫做 Pluribus的人工智能选手在长达12天的鏖战中，打败了12名世界顶级职业玩家。

目录

1. 强化学习发展历史简述

1.1 动物实验心理学中的效应定律

强化学习是一种基于反馈的学习，即存在一个智能体，能够感知环境，根据环境状态做出动作，并从环境接收反馈信息，以此调整自身的行动策略。这种基于反馈进行学习的朴素思想很早就被研究者观察到了。心理学家Edward Thorndike在1911年将其总结为“效应定律(Law of effect)”[50]：

“面对同样的情境时，动物可能产生不同的反应。在其他条件相同的情况下，如果某些反应伴随着或紧随其后能够引起动物自身的满足感，则这些反应将与情境联系得更加紧密。因此，当这种情境再次发生的时候，这些反应也更有可能再出现。而在其他条件相同的情况下，如果某些反应给动物带来了不适感，则这些反应与情境的联系将被减弱，所以当这种情境再次发生时，这些反应便越来越不容易再现。更大的满意度或更大的不适感，决定了更强化或更弱化的联系。”

与效果定律类似的，还有“练习定律(Law of exercise)”：

“练习次数的多寡，影响刺激和反应之间练习的稳固程度。练习越多，练习越紧密，小鸡越清楚要采取什么行动，逃脱的速度越快；练习越少，练习就不够紧密，小鸡就越难找到出口。”

此后，在动物学习领域，巴甫洛夫对条件反射的研究中开始使用“强化”一词。这里的“强化”，也包含了弱化过程，即对刺激事件的忽略或终止。

1.2 早期计算机领域关于试错学习的探索

这种基于反馈，或者称基于试错的学习思想，得到了计算机领域学者的关注。图灵在1948年的报告[51]中描述了一种“快乐-痛苦”的机器对效应定律进行演绎：

“当达到无预设动作的状态时，随机选择一些没有遇到过的数据，记录并试探性地应用这些数据。如果发生了痛苦刺激，停止所有动作试探。如果发生了愉悦刺激，则一直保持动作试探。”

1.3 试错学习与最优控制

这种“试错”学习方式，与“最优控制”的理念不谋而合。“最优控制”的目标是使得动态系统随时间变化的某种度量最大化或者最小化[53]。从控制的角度，试错学习的一系列动作实际上是时序决策的结果。贝尔曼于1957年提出了最优控制问题的离散随机版本，并用马尔可夫决策过程(Markov decision process, MDP )进行形式化描述[52]。此后，Ronald Howard在1960年开发出了MDP的策略迭代方法[54]，为现代强化学习理论和算法打下了坚实的基础。

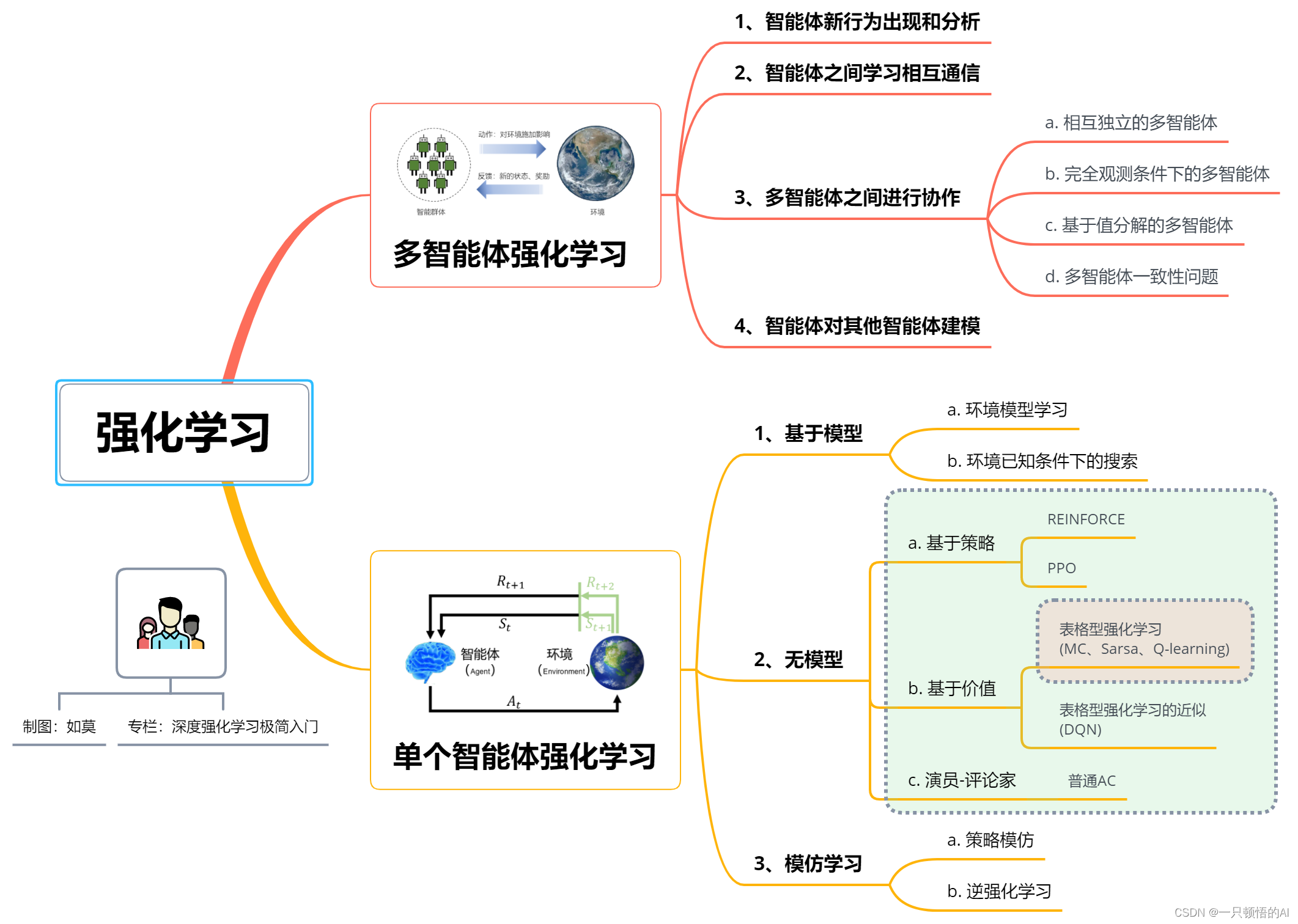
1.4 强化学习分类

图1 强化学习的不完全分类

处理马尔可夫决策过程有三类基本方法：动态规划(dynamic programming, DP)、蒙特卡洛方法(Monte Carlo, MC)和时序差分(temporal difference, TD)。动态规划方法具有严格而清晰的数学基础且已经被深入研究，但它需要完整而精确的环境模型。这里的环境模型，简称模型，一般指环境的状态转移函数：在当前状态下智能体执性某个动作后，环境如何转移到下一个状态。蒙特卡洛方法和时序差分(Temporal difference, TD)都不需要环境模型，属于无模型强化学习方法。蒙特卡洛方法在环境交互数据充分的条件下能够准确估计状态和动作的价值，从而收敛到有效的策略，但难以应用一步一步的增量式更新计算方式。时序差分方法用前后状态收益估计的差分来驱动价值函数的更新，能够增量式地更新，但在稳定性上有所欠缺。此外，在获得大量与环境交互的优质样本情况下，可以直接对策略进行监督学习，即模仿学习，如智能体行为克隆等。本文主要关注无模型强化学习方法。

强化学习中智能体的目标是找到一种最优策略用以最大化累积奖励和的期望。为了寻找最优策略，有两种可行方案：一种方案是准确估计每一个状态下所有动作的预期收益，最优动作自然就能通过贪婪策略得到，称为基于价值(函数)的强化学习。另一种方案是根据环境给出的奖励信号直接优化策略函数，称为基于策略(函数)的强化学习。

1.4.1 基于价值的强化学习算法

基于价值的强化学习方法，其核心是准确估计状态-动作对的值函数，时序差分思想在这类方法起到了核心作用。时序差分背后的思想可以追溯到Minsky在1954年发表的博士论文[57]，该论文认为预期收益是一种次级强化物，可以产生类似于初级强化物（例如食物或者疼痛）产生的刺激。Arthur Samuel在1959年开发了一个包含时序差分思想的算法用于跳棋程序[58]。20世纪80到90年代，Sutton和Barto等在时序差分思想的基础上建立了一个经典的条件反射心理学模型[55][56]，并且开发了“演员-评论家”(actor-critic)架构用于解决小车平衡杆问题[59]。Sutton在1988年将时序差分从控制中分离出来，将其作为一般的预测方法进行研究[60]。Watkins于1989年在他的博士论文中提出了著名的 学习算法[61]，将时序差分与最优控制结合在一起，大大推动了强化学习的研究进程。此后，Gerry Tesauro在1992年开发的基于时序差分的西洋双陆棋程序TD-Gammon[89]取得了巨大的成功，让强化学习领域得到了更多的关注。

以 学习为代表的基于价值的强化学习算法，使用一张 值表存储每个状态下做出各种动作所对应的未来收益的估计，获得新的交互数据后，使用时序差分方法对 值表进行更新。这种基于表格更新的算法称为表格型强化学习算法。表格型强化学习算法在理论证明和一些简单的离散状态和离散动作空间问题中是十分有用的，但缺点也很明显。当问题的状态和动作数量巨大或者是连续的，表格型算法无论在内存还是填充数据所需时间上都是难以满足需要的。为此，面对新的状态，从以往经历过的状态出发，去归纳和总结进而做出合理的决策是可行的方案。但是，新的状态与以往的状态有多相似？做出的决策应该参考多少？这些都是需要解决的问题。实际上，这是将一个有限子集的经验进行推广来近似一个大得多的子集的问题，又称为泛化问题。解决泛化问题通常使用函数逼近。

基于函数逼近的强化学习方法最早出现在Samuel的跳棋程序[58][62]中，Samuel按照Shannon的建议[63]，通过特征的线性组合来近似下棋策略所依赖的价值函数。为了表达特征之间的相互关系，基于多项式基、傅立叶基[64]的函数逼近方法逐渐被开发。粗编码[65]和瓦片编码[66][67][68][69][70]，都是基于特征的覆盖来算不同特征的值函数。径向基函数(radius basis function, RBF)[71][71][72]是粗编码和瓦片编码的自然扩展，即用一组高斯函数作为特征的线性逼近函数或者非线性逼近函数。RBF网络具有很强的表达能力，其缺点是计算复杂高且较为依赖参数设定。人工神经网络(artificial neural network, ANN)也很早就被广泛应用于强化学习中的非线性函数逼近[73][74][75][76]。而随着近年来深度神经网络的空前发展，各种高效ANN模型的出现是现代强化学习能够取得令人赞叹表现的重要原因之一。

人工神经网络具有悠久的研究历史且应用广泛，最近一二十年出现的深度神经网络(deep neural network, DNN)[18][19]更是表现出了惊人的表征能力。一个ANN是由相互连接的具有类似人和动物神经元功能的单元组成的网络。这些单元的输入输出特性一般具有一定的非线性区域，即对输入特征在线性组合的基础上增加激活函数，以增加对输入信号的非线性表征能力。一个ANN可以具有多个由神经单元组成的层，那些输入为其他层的输出，而其输出为其他层的输入的层，称为隐层。Cybenko在1989年证明[77]，如果一个ANN拥有一个隐层，并且这个隐层包含足够多数量的激活单元，则这个ANN可以在网络输入空间的一个紧凑区域内以任意精度逼近任意连续函数。但是，在后来的理论和实际应用中都发现，对于很多人工智能任务中的复杂函数，使用多层次的网络是一种更容易实现的逼近方式[78]。因此，ANN朝着层数增加的方向发展，高层的抽象是许多底层抽象的层次化组合，即深度学习。基于梯度反向传播[79]以及其他一些防止过拟合[80]和梯度消失[81]的方法，可以对一些更深的网络进行训练。视觉领域的卷积神经网络（convolutional neural network, CNN）[18]、深度残差网络[20]，自然语言处理领域的循环神经网络（recurrent neural network, RNN）[83][85]、Transformer结构[85]等，都是优秀的基于深度学习的人工智能感知模型。

ANN在强化学习中的应用主要体现在对价值函数和策略函数的逼近。Barto等人在1982年使用一个双层神经网络来学习一个非线性控制策略[86]，并指出第一层用于自动学习合适的特征表征。Barto、Sutton和Watkins等人在1990年发表论指出，ANN在解决序列决策问题的函数逼近方法中可以发挥重要作用[87]。Williams在1992年开发的REINFORCE算法[88]，使用ANN作为智能体的策略函数，并使用反向传播方法进行训练。Tersauro在1992年开发的TD-Gammon程序[89]可以自动玩西洋双陆棋，展示了使用ANN进行函数逼近在强化学习中的巨大潜力。Silver等人在2015年提出的DQN(deep Q-network)[31]方法，用深度神经网络对Q网络的值函数进行拟合，并使用经验重放池和目标网络稳定训练过程。DQN使用卷积神经网络处理视频游戏的原始数据，在Atari视频游戏中达到了人类玩家的水平。在DQN之后，强化学习和深度学习相结合成为强化学习研究新范式，涌现出了大量优秀的深度强化学习 (deep reinforcement learning, DRL)算法[90][91][92][93][94][95][96][97]。

1.4.2 基于策略的强化学习算法和“演员-评论家”算法

基于价值的深度强化学习算法虽然在视频游戏等领域取得了突破，但是依然难以处理连续动作空间的任务。而基于策略的方法能够很好地适用于连续动作环境，比如机械控制问题。

基于策略的强化学习方法直接学习参数化的策略函数，此时价值函数可以用于策略函数的学习，但不是必需的。最早的基于策略的强化学习算法应是Williams在1992年开发的REINFORCE算法[88]。REINFORCE是一种基于蒙特卡洛的策略梯度算法，该算法基于蒙特卡洛思想对策略函数参数相对于长期累积奖励和期望的梯度进行估计，并使用梯度提升算法更新策略函数的参数。REIFFORCE算法中策略函数参数的每一次更新都需要使用整个任务的总收益，只有在任务结束后才能进行更新，并且每一步的决策都使用相同的收益(整个分幕的收益)进行强化。后续提出的改进算法，只考虑当步以后的收益，可以加快算法收敛速度，减少与环境的交互次数。REINFORCE算法使用任务结束后的收益来更新策略参数，这种收益是一种无偏估计。但该算法的更新需要等任务（甚至是许多次任务）结束后才能更新策略函数。2000年前后，Marbach、Tsitsiklis和Sutton等人先后推导出了策略梯度理论[98][99]，即策略对收益的梯度可以用动作的价值函数和策略的梯度进行表示，REINFORCE是其中的一种特殊情况。基于策略梯度理论，价值函数和策略函数得到统一，形成了“演员-评论家”结构的强化学习智能体架构。近些年出现的表现出色的深度强化学习智能体大多基于此结构。当强化学习算法中的策略函数被参数化，并且使用梯度进行更新，这类算法都称为策略梯度算法。2016年以后，许多优秀的策略梯度算法陆续被提出[100][101][102][97]，其中近端策略优化算法(proximal policy optimization, PPO)[102]将策略梯度进行限制，较好的稳定了策略梯度算法的参数更新。基于PPO算法开发的电子游戏多智能体OpenAI Five[33]在多人即时战略游戏Dota2中达到了顶尖人类玩家的水平。

2. 强化学习能做什么

强化学习是实现智能决策的有效途经，与决策相关的问题都可以尝试用强化学习方案去解决，应用是相当广泛的。这里仅仅举几个简单的例子加以说明。

2.1 使用强化学习实现控制功能

图2 使用强化学习控制模拟飞船着陆

图2展示了使用强化学习控制模拟飞船着陆的过程。智能体（飞船）能够观测到着陆台的坐标以及自身的坐标，任务是通过控制发动机动力的大小和方向以安全的速度和姿势停到指定区域。

图3 使用强化学习控制星际争霸游戏智能体

图3展示了使用强化学系控制智能体完星际争霸游戏的画面。这里面有诸多控制单元，如果将每个单元视为不同的单元，具备各自的观测和动作空间，则会变成一个多智能体强化学习问题。此时需要考虑团体的奖励分配、团队协作和探索等问题。

2.2 使用强化学习玩棋牌类游戏

图4 围棋

图5 麻将

2.3 使用强化学习优化物流

图6 使用强化学习优化物流运输

图6为中国科学院自动化研究所群体决策智能实验室及第平台上的物流运输仿真器是及第自主开发的物流运输环境，其中的运输网络由节点集和有向边集组成。物流运输环境中的网络由10个节点和13条边组成。每个节点包含生产量、需求量和库存量，当库存量超过上界时，库存量为上界值。环境的控制目标为满足运输网络中所有节点需求的同时，最小化整个物流系统的成本。

2.4 使用强化学习实现核聚变反应控制

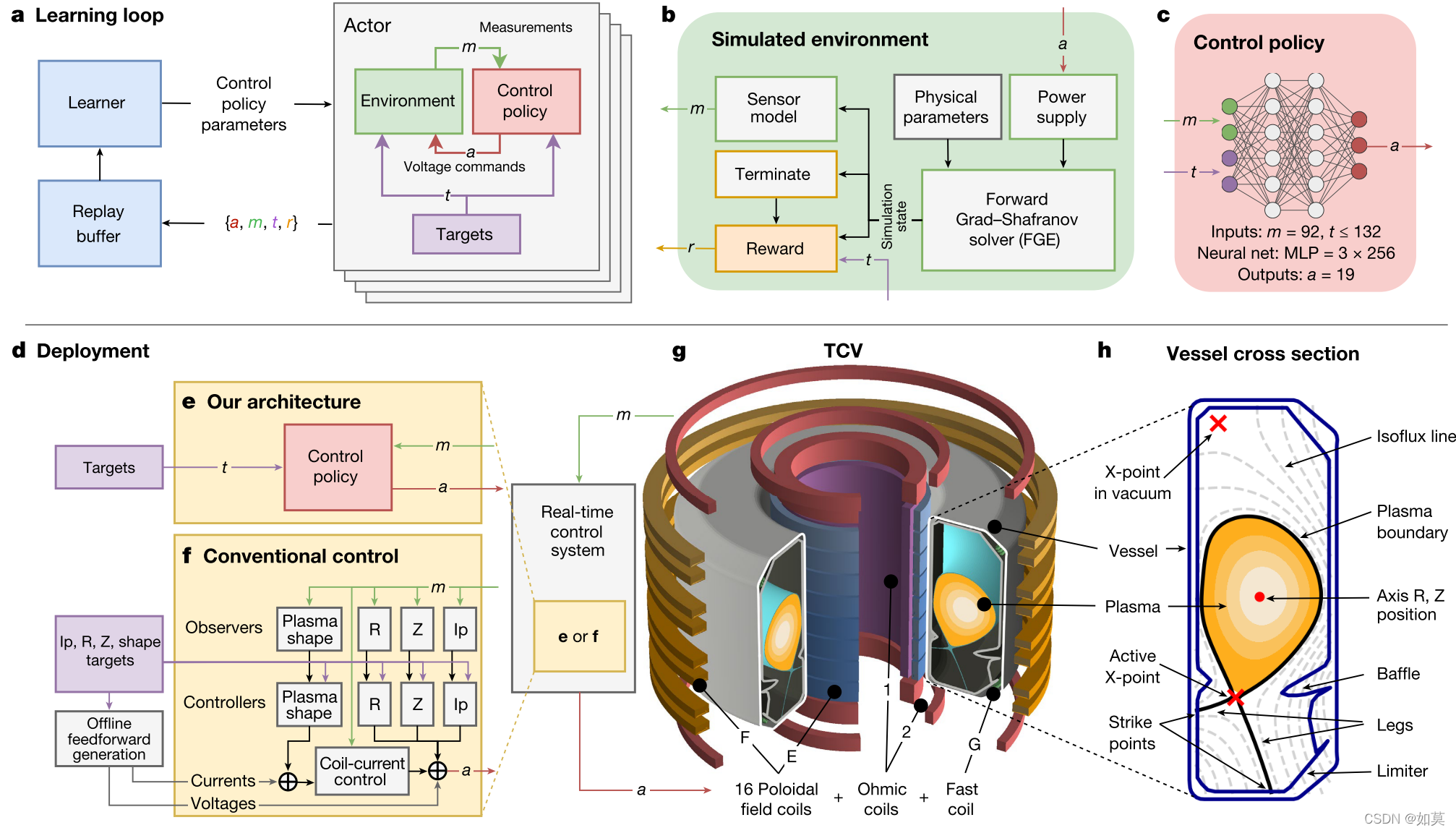
图7 使用强化学习实现核聚变反应控制

图7为DeepMind于2022年初在Nature杂志上发表的使用强化学习实现核聚变反应控制论文插图。这篇文章大大冲击了强化学习只能在游戏或者仿真环境中发挥作用的传统印象，让大家意识到强化学习也能在实际的工业控制中发发挥作用。

2.5 使用强化学习实现路由控制协议

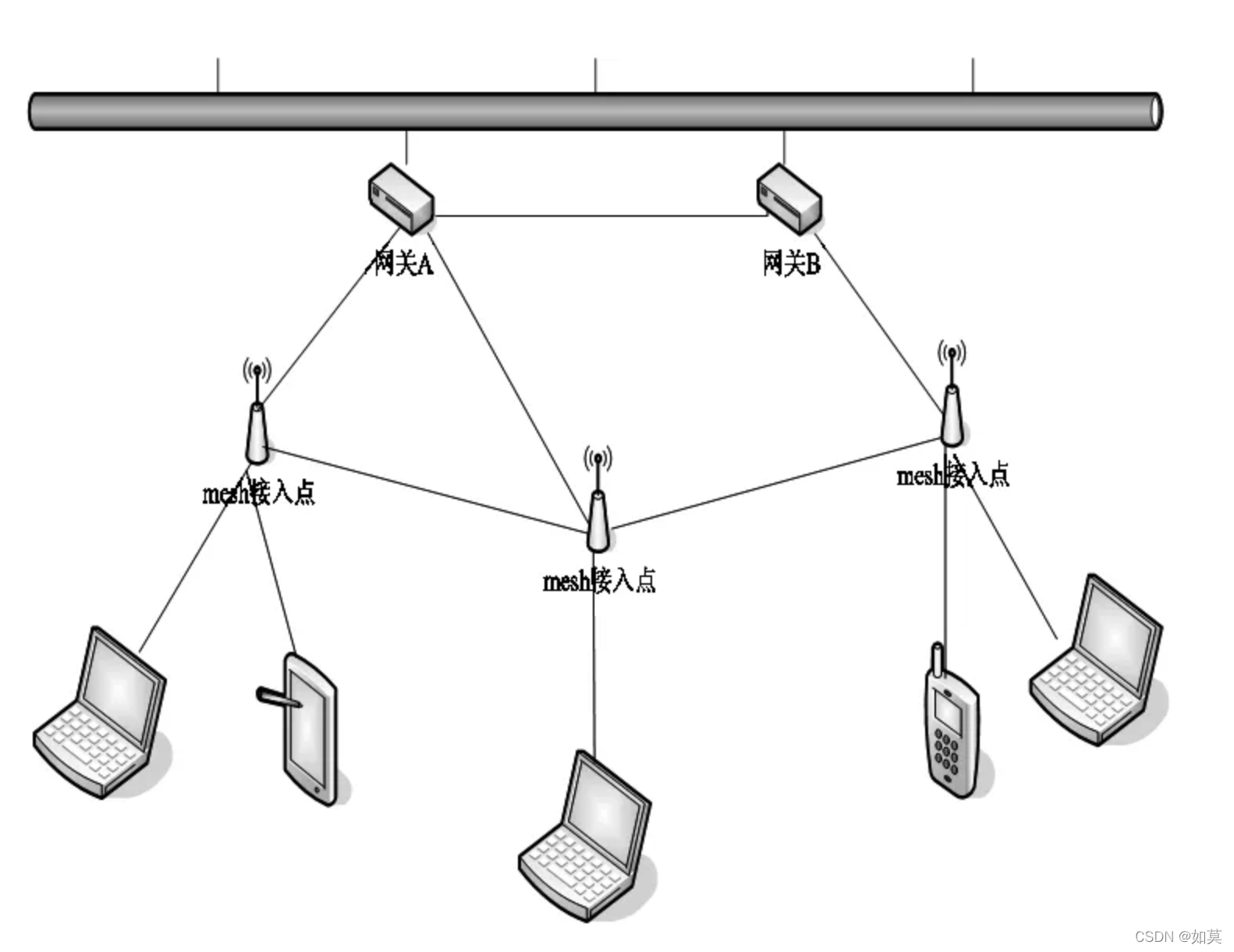
图8 使用强化学习优化路由协议

使用强化学习进行路由协议控制当年Littman等大佬早很多年前就开始研究了，但是当时的表征和计算能力有限，并未取得太大的效果。现在随着深度学习的发展，强化学习智能体“脑袋扩容”了，因此有些学者又开始尝试使用强化学习解决包路由的问题。

2.6 使用强化学习控制自动驾驶车辆

图9 使用强化学习控制自动驾驶车辆

参考文献

[18] LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[C]. Proceedings of the IEEE. 1998.
[19] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT Press. 2016.
[20] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]. IEEE Conference of Computer Vision and Pattern Recognition. 2016: 770-778.
[21] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[C]. The 3rd International Conference on Learning Representations. 2015: 1–14.
[22] Girshick R. Fast R-CNN[C]. Proceedings of the IEEE International Conference on Computer Vision. 2015: 1440–1448.
[23] Redmon J, Divvala S K, Girshick R B. You only look once: unified, real-time object detection[C]. IEEE Conference on Computer Vision and Pattern Recognition. 2016: 779-788.
[24] Mikolov T, Corrado G, Chen K, et al. Efficient estimation of word representations in vector space[C]. International Conference on Learning Representations. 2013: 1–12.
[25] Sutskever I, Vinyals O, V.Le Q. Sequence to sequence learning with neural networks[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems. 2014, 2: 3104–3112.
[26] Devlin J, Chang M, Lee K, et al. BERT: Pre-training of deep bidirectional transformers for language understanding. Conference of the North American Chapter of the Association for Computational Linguistics - Human Language Technologies. 2019, 1: 4171–4186.
[27] Howard J, Ruder S. Universal language model fine-tuning for text classification. Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Dissertations). 2018.
[28] Purwins H, Li B, Virtanen T, et al. Deep learning for audio signal processing. Journal of Selected Topics of Signal Processing. 2019, 13(2): 206–219.
[29] Luo H, Zhang S, Lei M. Simplified self-attention for transformer-based end-to-end speech recognition[C]. Proceedings of IEEE Spoken Language Technology Workshop. 2021: 75–81.
[30] Silver D, Huang A, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature. 2016, 529(7587): 484–489.
[31] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature. 2015, 518(7540): 529–533.
[32] Vinyals O, Babuschkin I, Czarnecki W M, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning[J]. Nature. 2019, 575(7782): 350–354.
[33] OpenAI Five: https:. openai.com/five/.
[34] Brown N, Sandholm T. Superhuman AI for multiplayer poker[J]. Science. 2019, 365(6456): 885–890.
[35] Wolpert H D, Tumer K. Optimal payoff functions for members of collectives[J]. Modeling Complexity in Economic and Social Systems. 2002: 355–369.
[36] Agogino K A, Tumer K. Unifying temporal and structural credit assignment problems[C]. The Third International Joint Conference on Autonomous Agents and Multiagent Systems. IEEE Computer Society, 2004: 980–987.
[37] Thien D, Kumar A, and Lau C H. Credit assignment for collective multiagent RL with global rewards[C]. Advances in Neural Information Processing Systems. 2018: 8102–8113.
[38] Tan M. Multi-agent reinforcement learning: Independent vs. Cooperative agents[C]. The 10th international conference on machine learning. 1993: 330–337.
[39] Lauer M, Riedmiller M. Distributed reinforcement learning in multi-agent networks[C]. The 7th International Conference on Machine Learning. 2000.
[40] Ye D, Liu Z, Sun M, et al. Mastering Complex Control in MOBA Games with Deep Reinforcement Learning[C]. The 34th AAAI Conference on Artificial Intelligence. 2020: 6672-6679.
[41] RoboCup: http:. robocup.drct-caa.org.cn/.
[42] 魏志鹏. RoboCup救援仿真中异构多智能体协作策略[D]. 南京: 南京邮电大学, 2016.
[43] Chen L, Qin S, Chen K, et al. Efficient role assignment with priority in Robocup3D[C]. Chinese Control and Decision Conference (CCDC). 2020: 2697-2702.
[44] 刘转. 基于多智能体系统的兵棋推演模型研究[D]. 武汉: 华中科技大学, 2016.
[45] 张瑶, 马亚辉. 体系对抗中的智能策略生成[J]. 中国信息化, 2018, 291(07):52-55.
[46] 强化学习在多智能体对抗中的应用研究[D]. 北京: 中国运载火箭技术研究院, 2019.
[47] 聂凯, 曾科军, 孟庆海,等. 人机对抗智能技术最新进展及军事应用[J]. 兵器装备工程学报, 2021, 42(6): 6-26.
[48] 李琛, 黄炎焱, 张永亮,等. Actor-Critic框架下的多智能体决策方法及其在兵棋上的应用[J]. 系统工程与电子技术. 2021, 43(3): 754-762.
[49] Busoniu L, Babuska R, Schutter B. A comprehensive survey of multiagent reinforcement learning[J]. IEEE Transactions on Systems, Man & Cybernetics (Part C Applications & Reviews). 2008, 38(2): 156-172.
[50] Thorndike E L. Animal intelligence[M]. Hafner, Darien, CT. 1911.
[51] Turing A M. Intelligent machinery[M]. Oxford University Press. 2004: 410-432.
[52] Bellman R E. A Markov decision process[J]. Journal of Mathematics and Mechanics. 1957: 679-684.
[53] Bellman R E. Dynamic programming[M]. Princeton University Press, Princeton, 1957.
[54] Howard Ronald. Dynamic programming and Markov process[M]. MIT Press, Cambridge, 1960.
[55] Sutton R S. Single channel theory: A neural theory of learning[J]. Brain Theory Newsletter. 1978(4): 72-75.
[56] Sutton R S. A unified theory of expectation in classical and instrumental conditioning[D]. California: Stanford University, 1978.
[57] Minsky M L. Theory of neural-analog reinforcement systems and its application to the brain-model problem[D]. New Jersey: Princeton University. 1954.
[58] Samuel A L. Some studies in machine learning using the game of checkers[J]. IBM Journal on Research and Development. 1959, 3(3): 210-229.
[59] Barto A G, Sutton R S, and Anderson C W. Neuronlike elements that can solve difficult learning control problem[J]. IEEE Transactions on System, Man, and Cybernetics, 1983, 13(5): 835-846.
[60] Sutton R S. Learning to predict by the method of temporal difference[J]. Machine Learning. 1988, 3(1): 9-44.
[61] Watkins C J C H. Learning from delayed rewards[D]. Cambridge: University of Cambridge, 1989.
[62] Samuel A L. Some studies in machine learning using the game of checkers II—Recent progress[J]. IBM Journal on Research and Development. 1967, 11(6): 601-617.
[63] Shannon C E. Programming a computer for playing chess[J]. Philosophical Magazine and Journal of Science. 1950, 41(314): 255-275.
[64] Konidaris G D, Osentoski S, and Thomas P S. Value function approximation in reinforcement learning using the Fourier basis[C]. The 25th Conference of the Association for the Advancement of Artificial Intelligence, 2011: 380-385.
[65] Waltz W G, Fu K S. A heuristic approach to reinforcement control systems[J]. IEEE Transactions on Automatic Control. 1965, 10(4): 390-398.
[66] Albus J S. A theory of cerebellar function[J]. Mathematical Biosciences. 1971, 10(1-2): 1307-1323.
[67] Albus J S. Brain, behavior, and robotics[M]. Byte Book, Peterborough, 1981.
[68] Shewchuk J, Dean T. Towards learning time-varying functions with high input dimensionality[C]. The 5th IEEE International Symposium on Intelligent Control. 1990: 383-388.
[69] Lin C S, Kim H. CMAC-based adaptive critic self-learning control[J]. IEEE Transactions on Neural Networks. 1991, 2(5): 661-670.
[70] Miller W T, Scalera S M, and Kim A. Neural network control of dynamic balance for a biped walking robot[C]. The 8th Yale Workshop on Adaptive and Learning Systems. 1994: 156-161.
[71] Powell M J D. Radius basis functions for multivariant interpolation: A review[M]. Algorithms for approximation. Clarendon Press, Oxford, 1987: 143-167.
[72] Poggio T, Girosi F. Regularization algorithms for learning that are equivalent to multiplayer networks[J]. Science. 1990, 247(4945): 978-982.
[73] Riedmiller M. Neural fitted Q iteration-first experiences with a data efficient neural reinforcement learning method[C]. The European Conference on Machine Learning. 2005: 317–328.
[74] Munos R, Szepesvari C. Finite-time bounds for fitted value iteration[J]. Journal of Machine Learning Research[J]. 2008, 9(3): 815-857.
[75] Antos A, Munos R, Szepesvari C. Fitted Q-iteration in continuous action-space MDPs[J]. Advances in Neural Information Processing Systems.2008, 53(2): 556-564.
[76] Lange S, Riedmiller M. Deep Auto-Encoder Neural Networks in Reinforcement Learning[C]. International Joint Conference on Neural Networks. 2010.
[77] Cybenko G. Approximation by superpositions of a sigmoidal function[J]. Mathematics of Control, Signal and Systems. 1989, 2(4): 303-314.
[78] Bengio Y. Learning deep architectures for AI[J]. Foundations and Trends in Machine Learning. 2009, 2(1): 1-27.
[79] Rumelhart D E, Hinton G E, and Williams R J. Learning Representations by Back Propagating Errors[J]. Nature. 1986, 323(6088):533-536.
[80] Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research. 2014, 15(1): 1929-1958.
[81] Ioffe S, Szegedy C. Batch Normalization: Accelerating deep network training by reducing internal covariate shift[J]. JMLR.org. 2015.
[82] Cho K. Learning phrase representations using RNN encoder-decoder for statistical machine translation[J]. Computer Science. 2014, https:. arxiv.org/abs/1406.1078.
[83] Giles C L, Kuhn G M, and Williams R J. Dynamic recurrent neural networks: theory and applications [J] IEEE Transactions on Neural Networks. 1994, 5(2): 153-156.
[84] Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation. 1997, 9(8):1735-1780.
[85] Vaswani A, Shazeer N, Parmar N. Attention Is All You Need[C]. Advances in Neural Information Processing Systems. 2017: 5999–6009.
[86] Barto A G, Anderson C W, and Sutton R S. Synthesis of nonlinear control surfaces by a layered associative search network[J]. Biological Cybernetics. 1982, 43(3): 175-185.
[87] Miller T, Sutton R S, and Werbos P J. Neural networks for control. Cambridge, MA, MIT Press, 1990: 5-58.
[88] Williams R J, Baird L C. A mathematical analysis of actor-critic architectures for learning optimal controls through incremental dynamic programming[C]. The 6th Yale Workshop on Adaptive and Learning Systems. 1990: 96-101.
[89] Tesauro G. TD-Gammon, a self-teaching backgammon program, achieve master-level play[J]. Neural Computation. 1994, 6(2): 215-219.
[90] Hasselt H V, Guez A, and Silver D. Deep reinforcement learning with double q-learning[C]. The 30th AAAI Conference on Artificial Intelligence, 2016.
[91] Wang Z, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning[C]. The 33rd International Conference on Machine Learning, ICML. 2015: 2939-2947.
[92] Fortunato M, Azar M G, Piot B, et al. Noisy networks for exploration[C]. The 6th International Conference on Learning Representations, ICLR. 2017.
[93] Bellemare M G, Dabney W, and Munos R. A distributional perspective on reinforcement learning[C]. The 34th International Conference on Machine Learning. 2017: 449–458.
[94] Dabney W, Rowland M, Bellemare M G, et al. Distributional reinforcement learning with quantile regression[C]. The 32nd AAAI Conference on Artificial Intelligence, 2018.
[95] Hessel M, Modayil M, Hasselt H V, et al. Rainbow: Combining improvements in deep reinforcement learning[C]. In 32nd AAAI Conference on Artificial Intelligence, 2018.
[96] Fujimoto S, Hasselt H V, Meger D. Addressing function approximation error in actor-critic methods[C]. The 35th International Conference on Machine Learning, ICML. 2018: 2587–2601.
[97] Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor[C]. The 35th International Conference on Machine Learning, ICML 2018: 2976–2989.
[98] Marbach P. Tsitsiklis J N. Simulation-based optimization of Markov reward processes[R]. LIDS-P-2411. 1998.
[99] Sutton R S, McAllester D A, Singh S P, et al. Mansour. Policy gradient methods for reinforcement learning with function approximation[C]. Advances in Neural Information Processing Systems. 2000: 1057–1063.
[100] Mnih V, Badia A P, Mirza L, et al. Asynchronous methods for deep reinforcement learning[C]. The 33rd International Conference on Machine Learning, ICML. 2016: 2850–2869.
[101] Schulman J, Levine S, Abbeel P, et al. Trust region policy optimization[C]. International Conference on Machine Learning, ICML. 2015: 1889–1897.
[102] Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms[J]. arXiv preprint. arXiv:1707.06347, 2017.
[103] Sutton R S, Barto A G. Reinforcement learning: An introduction[M]. MIT Press, Cambridge, 1998.
[104] Foster D J, Wilson M A. Reverse replay of behavioural sequences in hippocampal place cells during the awake state[J]. Nature. 2006, 440(7084): 680–683.
[105] Singer AC, Frank L M. Rewarded outcomes enhance reactivation of experience in the hippocampus[J]. Neuron. 2009, 64(6): 910–921.
[106] McNamara C G, et al. Dopaminergic neurons promote hippocampal reactivation and spatial memory persistence[J]. Nature neuroscience. 2014.
[107] White A, Modayil J, Sutton R S. Surprise and curiosity for big data robotics[C]. Workshops at the Twenty-Eighth AAAI Conference on Artificial Intelligence. 2014.
[108] Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay[C]. The 4th International Conference on Learning Representations, ICLR. 2016.
[109] Atherton L A, Dupret D, Mellor J R. Memory trace replay: the shaping of memory consolidation by neuromodulation[J]. Trends in Nneurosciences. 2015, 38(9):560–570.
[110] Olafsdottir H F, Barry C, Saleem A B, et al. Hippocampal place cells construct reward related sequences through unexplored space[J]. Elife. 2015, 4: e06063.
[111] 安波, 史忠植. 多智能体系统研究的历史、现状及挑战.[J] 中国计算机学会通讯. 2014, 10(9): 8-14.
[112] 丁明刚. 基于多智能体强化学习的足球机器人决策策略研究[D]. 合肥: 合肥工业大学, 2017.
[113] 梅乐. 基于多智能体的多机器人跟踪控制研究[D]. 合肥: 合肥工业大学, 2016.
[114] 段勇, 徐心和. 基于多智能体强化学习的多机器人协作策略研究[J]. 系统工程理论与实践. 2014, 34(5):1305-1310.
[115] 汪伟, 张效义, 胡赟鹏. 基于无线传感网的分布式协调调制识别算法[J]. 计算机应用研究. 2014, 31(5): 1524-604.
[116] 高岐. 基于语义的家居多智能体协作决策方法的研究与实现[D]. 重庆: 重庆邮电大学, 2019.
[117] 刘鑫, 于振中, 郑为凑, 等. 多机器人远程监控系统的多智能体控制结构[J]. 计算机工程, 2014(2).
[118] 许少伦, 严正, 冯冬涵,等. 基于多智能体的电动汽车充电协同控制策略[J]. 电力自动化设备, 2014, 034(011):7-13,21.
[119] 杨涛. 基于多智能体的区域交通信号控制系统研究[D]. 成都: 西华大学, 2016.
[120] 盖翔. 基于多智能体的能量路由器调度优化方法研究[D]. 沈阳: 东北大学, 2015.
[121] Yu C, Lan J, Guo Z, et al. DROM: Optimizing the Routing in Software-Defined Networks with Deep Reinforcement Learning. IEEE Access. 2018, 6©: 64533–64539.
[122] 黄林. 基于深度强化学习的无线传感器网络调度与路由优化[D]. 武汉: 华中科技大学, 2019.
[123] Armbrust M, Fox A, Griffith R, et al. A review of cloud computing[J]. Communication of the ACM. 2010, 53(4): 211-225.
[124] Rong J, Qin T, An B, et al. Pricing optimization for selling reusable resources[C]. International Joint Conference on Autonomous Agents and Multi-Agent Systems. 2017.
[125] Panait L, Luke S. Cooperative multi-agent: the state of the art[J]. Journal of Autonomous Agents and Multi-Agent Systems. 2005, 11(3): 387-434.
[126] Huhns M N. Distributed artificial intelligence[M]. Pitman Publishing Ltd… London, England.
[127] Bound A H, Grasser. Readings in distributed artificial intelligence[M]. Morgan Kaufmann Publisher. San Mateo, CA.
[128] Vinyals O, Babuschkin I, Czarnecki W M, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning[J]. Nature. 2019, 575(7782): 350–354
[129] Jaderberg M, Czarnecki W M, Dunning I. Human-level performance in 3D multiplayer games with population based reinforcement learning[J]. Science, 865(May): 859–865.
[130] 韩伟. 电子市场环境下的多智能体学习与协商[D]. 上海: 华东师范大学, 2006.
[131] 梁天新, 杨小平, 王良,等. 基于强化学习的金融交易系统研究与发展[J]. 软件学报, 2019, 030(003): 845-864.
[132] Littman M L. Markov games as a framework for multi-agent reinforcement learning[C]. Machine Leaning Proceedings. 1994: 157-163.
[133] Kaelbling L P, Littman M L, Cassandra A R. Planning and acting in partially observable stochastic domains[J]. Artificial Intelligence. 1998: 99-134.
[134] Smith T, Simmons R. Heuristic search value iteration for POMDPs[C]. Proceedings of Uncertainty in Artificial Intelligence. 2004.
[135] Silver D, Veness J. Monte-Carlo planning in large POMDPs[C]. Advances in Neural Information Processing Systems. 2010.
[136] Bernstein D S, Givan R, Immerman N, et al. The complexity of decentralized control of Markov decision processes[J]. Mathematics of Operations Research. 2002, 27(4), 819-840.
[137] Nair R, Tambe M, Yokoo M, et al. Taming decentralized POMDPs: Towards efficient policy computation for multiagent settings[C]. International Joint Conference on Artificial Intelligence. 2003: 705–711.
[138] Nair R, Roth M, Yohoo M. Communication for improving policy computation in dis- tributed POMDPs[C]. International Joint Conference on Autonomous Agents and Multi Agent Systems. 2004: 1098–1105.
[139] Hu J, Wellman M P. Multiagent reinforcement learning: theoretical framework and algorithm[C]. The International Conference on Machine Learning. 1999: 242-250.
[140] Hu J, Wellman M P. Nash Q-Learning for general-sum stochastic games[J]. The journal of Machine Learning Research. 2003, 4: 1039-1069.
[141] Heinrich J, Silver D. Deep reinforcement learning from self-play in imperfect-information games[C]. NIPS Deep Reinforcement Learning Workshop. 2016.
[142] Greenwald A, Hall K, Serrano R. Correlated Q-learning[C]. The International Conference on Machine Learning. 2003.
[143] Könönen, V. Asymmetric multiagent reinforcement learning[C]. IEEE/WIC International Conference on Intelligent Agent Technology. 2004: 336-342.
[144] Wang X, Sandholm T. Reinforcement learning to play an optimal Nash equilibrium in team Markov games[J]. Robotics & Autonomous, 2002: 1571-1578.
[145] Chalkiadakis G, Boutilier C. Sequential decision making in repeated coalition formation under uncertainty[C]. International Joint Conference on Autonomous Agents and Multiagent Systems. 2008: 342-349.
[146] Albrecht S V, Stone P. Autonomous Agents Modelling Other Agents: A Comprehensive Survey and Open Problems[J]. Artificial Intelligence. 2017, 258: 66-95.
[147] Hernandez-Leal P, Kartal B, Taylor M E. A survey and critique of multiagent deep reinforcement learning[J]. Autonomous Agents and Multi-Agent Systems. 2019, 33(6), 750–797.
[148] Tampuu A, Matiisen T, Kodelja D, et al. Multiagent cooperation and competition with deep reinforcement learning[C]. PLOS ONE. 2017, 12(4).
[149] Bansal T, Pachocki J, Sidor S, et al. Emergent Complexity via Multi-Agent Competition[C]. International Conference on Machine Learning, 2018.
[150] Gullapalli V, Barto A G. Shaping as a method for accelerating reinforcement learning[C]. IEEE international symposium on intelligent control. 1992: 554–559.
[151] Raghu M, Irpan A, Andreas J, et al. Can Deep Reinforcement Learning solve Erdos-Selfridge-Spencer Games?[C]. The 35th International Conference on Machine Learning, 2018.
[152] Spencer J. Randomization, derandomization and antirandomization: three games[J]. Theoretical Computer Science. 1994, 131(2): 415–429.
[153] Lazaridou A, Peysakhovich A, Baroni M. Multi-Agent Cooperation and the Emergence of (Natural) Language[J]. International Conference on Learning Representations, 2017.
[154] Fudenberg D, Tirole J. Game Theory[M]. MIT Press, 1991.
[155] Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of machine learning research. 2008, 9: 2579–2605.
[156] Zahavy T, Ben-Zrihem N, Mannor S. Graying the black box: Understanding DQNs[C]. International Conference on Machine Learning. 2016:1899–1908.
[157] Mordatch I, Abbeel P. Emergence of grounded compositional language in multi-agent populations[C]. The 32nd AAAI Conference on Artificial Intelligence. 2018.
[158] Foerster J N, Assael Y M, Freitas, N, et al. Learning to communicate with deep multi-agent reinforcement learning[C]. Advances in Neural Information Processing Systems. 2016: 2145–2153.
[159] Kraemer L, Banerjee B. Multi-agent reinforcement learning as a rehearsal for decentralized planning[J]. Neurocomputing. 2016: 82–94.
[160] Lowe R, Wu Y, Tamar A. Multi-agent actor-critic for mixed cooperative-competitive environments[C]. Proceedings of Conference on Neural Information Processing Systems. 2017, 6379–6390.
[161] Sukhbaatar S, Szlam A, Fergus R. Learning multiagent communication with backpropagation[C]. Advances in Neural Information Processing Systems. 2016: 2252–2260.
[162] Peng P, Yuan Q, Wen Y, et al. Multiagent Bidirectionally-Coordinated Nets for Learning to Play StarCraft Combat Games[C]. Advances in Neural Information Processing Systems. 2017.
[163] Schuster M, Paliwal K. Bidirectional recurrent neural networks[J]. IEEE Transactions on Signal Processing. 1997, 45 (11): 2673–2681.
[164] He H, Boyd-Graber J, Kwok K. Opponent modeling in deep reinforcement learning[C]. The 33rd International Conference on Machine Learning. 2016: 2675–2684.
[165] Hong Z-W, Su S-Y, Shann T-Y, et al. A deep policy inference Q-network for multi-agent systems[C]. International Conference on Autonomous Agents and Multiagent Systems. 2018.
[166] Jaderberg M, Mnih V, Czarnecki W M. Reinforcement Learning with Unsupervised Auxiliary Tasks[C]. International Conference on Learning Representations. 2017.
[167] Sutton R S, Modayil J, Delp T. Horde: A scalable real-time architecture for learning knowledge from unsupervised sensorimotor interaction[C]. The 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 2. 2011: 761–768.
[168] Raileanu R, Denton E, Szlam A, et al. Modeling others using oneself in multi-agent reinforcement learning[C]. International Conference on Machine Learning. 2018.
[169] Li S, Wu Y, Cui X. Robust multi-agent reinforcement learning via minimax deep deterministic policy gradient[C]. AAAI Conference on Artificial Intelligence. 2019.
[170] Morimoto J, Doya L. Robust reinforcement learning[J]. Neural computation. 2005, 17 (2): 335–359.
[171] Pinto L, Davidson J, Sukthankar R. Robust adversarial reinforcement learning[C]. The 34th International Conference on Machine Learning. 2017: 2817–2826.
[172] Sunehag P, Lever G, Gruslys A, et al. Value-decomposition networks for cooperative multi-agent learning based on team reward[C]. The 17th International Conference on Autonomous Agents and MultiAgent Systems, 2018: 2085–2087.
[173] Rashid T, Samvelyan M, Witt C S, et al. Qmix: Monotonic value function factorization for deep multi-agent reinforcement learning[C]. International Conference on Machine Learning. 2018: 4292–4301.
[174] Son K, Kim D, Kang W J, et al. Qtran: Learning to factorize with transformation for cooperative multi-agent reinforcement learning[C]. International Conference on Machine Learning. 2019: 5887–5896.
[175] Wang J, Ren Z, Liu T, et al. QPLEX: Duplex Dueling Multi-Agent Q-Learning[C]. International Conference on Learning Representations. 2021.
[176] Varshavskaya P, Kaelbling L P, Rus D. Efficient distributed reinforcement learning through agreement[C]. In Distributed Autonomous Robotic Systems. 2009: 367–378.
[177] Kar S, Moura J M F, Poor H V. QD-learning: A collaborative distributed strategy for multi-agent reinforcement learning through consensus + innovations[J]. IEEE Transactions on Signal Processing. 2013, 61(7):1848–1862.
[178] Kar S, Moura J M F, Poor H V. Distributed reinforcement learning in multi-agent networks. IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP). 2013: 296–299.
[179] Zhang K-Q, Yang Z-R, Liu H, et al. Fully decentralized multi-agent reinforcement learning with networked agents[C]. The 35th International Conference on Machine Learning, 2018: 5872–5881.
[180] Macua S V, Chen J-S, Zazo S, et al. Distributed policy evaluation under multiple behavior strategies[J]. IEEE Transactions on Automatic Control. 2015, 60(5):1260–1274.
[181] Wai H-T, Yang Z-R, Wang Z-R, et al. Multi-agent reinforcement learning via double averaging primal-dual optimization[C]. In Advances in Neural Information Processing Systems. 2018: 9649–9660.
[182] Zhang K-Q, Yang Z-R, Basar T. Networked multi-agent reinforcement learning in continuous spaces[C]. In 2018 IEEE Conference on Decision and Control (CDC), 2018: 2771–2776.
[183] Suttle W, Yang Z-R, Zhang K-Q, et al. A multi-agent off-policy actor-critic algorithm for distributed reinforcement learning[J]. arXiv preprint. arXiv:1903.06 372, 2019.
[184] Bertsekas D P, Tsitsiklis J. Neuro-dynamic programming[M]. Athena Scientific, Belmont, 1996.
[185] Puterman M L. Markov decision processes—Discrete stochastic dynamic programming[M]. John Wiley & Sons, Inc., New York, 1994.
[186] Ross S M. Stochastic processes, second edition[M]. John Wiley & Sons Inc. 1995.
[187] Wiering M A. Explorations in efficient reinforcement learning[D]. Amsterdam: Universiteit van Amsterdam, 1999.
[188] Dayan P. The convergence of TD( ) for general . Machine Learning. 1992, 8(3):341–362.
[189] Degris T, White M, Sutton R S. Linear off-policy actor-critic[J]. The 29th International Conference on Machine Learning. 2019.
[190] Nair A, Srinivasan P, Blackwell S, et al. Massively parallel methods for deep reinforcement learning[J]. CoRR, vol. abs//1507.04296. 2015: 1–14.
[191] Clemente A V, Castejón H N, Chandra A. Efficient parallel methods for deep reinforcement learning[J]. CoRR, vol. abs/1705.04862. 2017: 1–9.
[192] Espeholt L, Soyer H, Munos R, et al. IMPALA: Scalable distributed deep-RL with importance weighted actor-learner architectures[C]. The 35th International Conference on Machine Learning. 2018, 4: 2263–2284.
[193] Luo M, Yao J, Liaw R, Liang E. IMPACT: Importance weighted asynchronous architectures with clipped target networks[C]. International Conference on Learning Representations. 2020: 1–14.
[194] Han S, Sung Y. Dimension-wise importance sampling weight clipping for sample-efficient reinforcement learning[C]. International Conference on Machine Learning. 2019: 4572–4584.
[195] Schulman J, Moritz P, Levine S. High-dimensional continuous control using generalized advantage estimation[C]. The 4th International Conference on Learning Representations. 2016: 1–14.
[196] Emanuel Todorov, Tom Erez, and Yuval Tassa. Mujoco: A physics engine for model-based control[C]. In Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on, pp. 5026– 5033. IEEE, 2012.
[197] Kingma D P, Ba J L. Adam: A method for stochastic optimization[C]. International Conference on Learning Representations. 2015: 1–15.
[198] Foerster J N, Farquhar G, Afouras T, et al. Counterfactual multi-agent policy gradients[C]. AAAI Conference on Artificial Intelligence. 2018.
[199] Wolpert D H, Tumer K. Optimal payoff functions for members of collectives. In Modeling Complexity in Economic and Social Systems[M]. World Scientific. 2002: 355–369.
[200] Konda V R, Tsitsiklis J N. Actor-critic algorithms[C]. Advances in Neural Information Processing Systems. 2000: 1008–1014.
[201] Hornik K. Multilayer feedforward networks are universal approximators[J]. Neural Networks. 1989, 2: 359–366.
[202] Cybenko G. Approximation by superpositions of a sigmoidal function[J]. Mathematics of Control, Signals, and Systems. 1989, 2: 303–314.
[203] Hoshen Y. Vain: Attentional multi-agent predictive modeling[C]. Advances in Neural Information Processing Systems. 2017: 2701–2711.
[204] Jiang J, Lu Z. Learning attentional communication for multi-agent cooperation[C]. Advances in Neural Information Processing Systems. 2018: 7254–7264.
[205] Singh A, Jain S, Sukhbaatar S. Learning when to communicate at scale in multiagent cooperative and competitive tasks[C]. Proceedings of the International Conference on Learning Representations. 2019.
[206] Das A, Gervet T, Romoff J. Tarmac: Targeted multi-agent communication[C]. International Conference on Machine Learning. 2019: 1538–1546.
[207] Zhang C, Lesser V. Coordinating multi-agent reinforcement learning with limited communication[C]. Proceedings of the 2013 International Conference on Autonomous Agents and Multi-agent Systems. 2013: 1101–1108.
[208] Tishby N, Pereira F C, Biale W. The information bottleneck method[C] The 37th Annual Allerton Conf. on Communication, Control, and Computing. 1999: 368–377.
[209] Alemi A A, Fischer I, Dillon J V, et al. Deep variational information bottleneck[C]. 5th International Conference on Learning Representations. 2017: 1–19.
[210] Don J. Statistical theory of passive location systems[J]. IEEE Transactions on Aerospace and Electronic Systems. 1984(2): 183–198.
[211] Al-Jazzar S O, Jaradat Y. AOA-based drone localization using wireless sensordoublets[J]. Physical Communication. 2020(42).
[212] Ho K C, Lu X, Kovavisaruch L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: analysis and solution[J]. IEEE Transactions on Signal Processing. 2007, 55(2): 684–696.
[213] Ma F, Guo F, Yang L. Low-complexity TDOA and FDOA localization: A compromise between two-step and DPD methods[J]. Digital Signal Processing. 2020, 96.
[214] Amar A, Weiss A J. Direct position determination in the presence of model errors-known waveforms[J]. Digital Signal Processing. 2006, 16(1): 52–83.
[215] Weiss A J. Direct position determination of narrowband radio transmitters[C]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). 2004, 2.
[216] Tirer T, Weiss A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters. 2016, 23(2): 192–196.
[217] Krzysztof B, Stefanski J. Bad geometry effect in the TDOA systems[J]. Polish Journal of Environmental Studies. 2007, 16: 11–13.
[218] Martin-Escalona I, Barcelo-Arroyo F. Impact of geometry on the accuracy of the passive-TDOA algorithm[C]. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications. 2008: 1–6.
[219] Sun B. Analysis of the influence of station placement on the position precision of passive area positioning system based on TDOA[J]. Fire Control & Command Control. 2011, 36: 129–132.
[220] Wang B, Xue L. Station arrangement strategy of TDOA location system based on genetic algorithm[J]. Systems Engineering and Electronics. 2009, 31: 2125–2128.
[221] Zhou G. Analysis of the influence of base station layout on location accuracy based on TDOA[J]. Command Control and Simulation, 2017, 39: 119–126.
[222] Shi Y, Eberhart R C. A modified particle swarm optimization[C]. Proceedings of the IEEE Congress on Evolutionary Computation. 1999: 69–73.
[223] Kennedy J, Eberhart R C. Swarm Intelligence[M]. San Mateo, CA, USA: Morgan Kaufmann, 2001.
[224] Tan M. Multi-agent reinforcement learning: Independent vs. cooperative agents[C]. Proceedings of the 10th International Conference on Machine Learning. 1993: 330–337.
[225] Matignon L, Laurent G, Fort-Piat N. Hysteretic q-learning: An algorithm for decentralized reinforcement learning in cooperative multi-agent teams[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS’07. 2007: 64–69.
[226] Matignon L, Laurent G, Fort-Piat N. Independent reinforcement learners in cooperative Markov games: A survey regarding coordination problems[J]. The Knowledge Engineering Review. 2012, 27(1): 1–31.
[227] Pennesi P, Paschalidis I. A distributed actor-critic algorithm and applications to mobile sensor network coordination problems[J]. IEEE Transactions on Automatic Control. 2010, 55(2):492–497.
[228] Prasad H, Prashanth L A, Bhatnagar S. Two-timescale algorithms for learning Nash equilibria in general-sum stochastic games[C]. Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems. 2015, 3: 1371–1379.
[229] Nedich A, Olshevsky A, Shi W. A geometrically convergent method for distributed optimization over time-varying graphs[C]. IEEE 55th Conference on Decision and Control (CDC). 2016: 1023–1029.
[230] Xiao L, Boyd S, Lall S. A scheme for robust distributed sensor fusion based on average consensus[C]. Proceedings of the 4th International Symposium on Information Processing in Sensor Networks. 2005: 63–70.
[231] Borkar V S, Stochastic approximation a dynamical systems viewpoint[M]. Hindustan Book Agency (lndia). 2008: 74–75.
[232] Fernández F, Veloso M. Probabilistic policy reuse in a reinforcement learning agent[C]. Proceedings of American Association for Artificial Intelligence. 2006.
[233] Wiering M, Otterlo M V. Reinforcement Learning: State-of-the-Art. Springer[M]. Berlin. 2012: 143–173.
[234] Haitham Bou Ammar, Eric Eaton, Mattliew E. Taylor. An automated measure of MDP similarity for transfer in reinforcement learning[C]. Proceedings of AAAI Workshop Technical Report. 2014, Vol. WS-14-07: 31–37.
[235] García J, Fernández F. Probabilistic Policy Reuse for Safe Reinforcement Learning[J]. ACM Transactions on Autonomous and Adaptive Systems. 2019 3(13): 14.1–14.24.
[236] Sunmola F T, Wyatt J L. Model transfer for Markov decision tasks via parameter matching[C]. Proceedings of the 25th Workshop of the UK Planning and Scheduling Special Interest Group. 2006.
[237] Brunskill E, Li LH. PAC-inspired Option Discovery in Lifelong Reinforcement Learning[C]. Proceedings of the 31st International Conference on Machine Learning. 2014, 32: 316–324.
[238] Fernández F, Veloso M. Learning domain structure through probabilistic policy reuse in reinforcement learning[J]. Progress in Artificial Intelligence. 2013: 13–27.
[239] Yang T, Hao J, Meng Z, et al. Efficient deep reinforcement learning via adaptive policy transfer[C]. Proceedings of International Joint Conference on Artificial Intelligence.2020: 3094–3100.
[240] Sutton R S, Precup D, Singh S P. Intra-Option learning about temporally abstract actions[C]. Proceedings of International Conference on Machine Learning. 1998: 556–564.
[241] Li S, Gu F, Zhu G, Zhang C. Context-aware policy reuse[C]. Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS. 2019, 2: 989–997.
[242] Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translation[C]. Proceedings of International Conference on Learning Representations. 2015.
[243] Brown T, Mann B, Ryder N. Language models are few-shot learners[C]. Proceedings of Advances in Neural Information Processing Systems. 2020, 33: 1877–1901.
[244] Bello I, Zoph B, Le Q. Attention augmented convolutional networks[C]. Proceedings ofthe IEEE International Conference on Computer Vision. 2019: 3285–3294.
[245] Pan J, Yang Qiang. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering. 2010, 10: 1345–1359.