简介
论文:https://arxiv.org/pdf/2207.12598.pdf
分类器指导将扩散模型的得分估计与图像分类器的梯度相结合,因此需要训练与扩散模型分开的图像分类器。
实验证明,在没有分类器的情况下,指导确实可以由纯生成模型执行
在无分类器指导中,联合训练了一个条件和无条件扩散模型,并将得到的条件和无条件分数估计结合起来,以获得样本质量和多样性之间的权衡,类似于使用分类器指导获得的结果
GUIDANCE
某些生成模型(如GANs和基于流的模型)的一个有趣的特性是,能够通过在采样时减少生成模型的噪声输入的方差或范围来执行截断或low temperature采样,这样会减少样本的多样性,同时提高每个样本的质量
BigGAN中的截断分别为低截断量和高截断量产生FID评分和Inception评分之间的权衡曲线
不幸的是,直接尝试在扩散模型中实现截断或低温采样是无效的。例如,在逆向过程中缩放模型得分或降低高斯噪声的方差会导致扩散模型生成模糊、低质量的样本。
CLASSIFIER GUIDANCE
为了在扩散模型中获得类似截断的效果,先前工作引入了分类器引导,其中扩散分数
ϵ
θ
(
z
λ
,
c
)
≈
−
σ
λ
∇
z
λ
l
o
g
p
(
z
λ
∣
c
)
\epsilon_θ(z_λ, c) ≈ −σ_λ∇_{z_λ} log p(z_λ|c)
ϵθ(zλ,c)≈−σλ∇zλlogp(zλ∣c)被修改,以包括辅助分类器模型
p
θ
(
c
∣
z
λ
)
p_θ(c|z_λ)
pθ(c∣zλ) 的对数似然梯度:
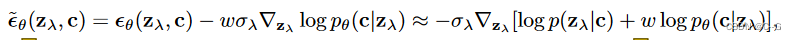
w 是控制分类器引导强度的参数,当从扩散模型采样时,使用这个修改后的分数
ϵ
~
θ
(
z
λ
,
c
)
\tilde{\epsilon}_θ(z_λ, c)
ϵ~θ(zλ,c) 代替
ϵ
θ
(
z
λ
,
c
)
\epsilon_θ(z_λ, c)
ϵθ(zλ,c),从分布中得到近似样本
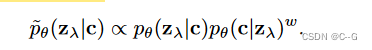
对分类器
p
θ
(
c
∣
z
λ
)
p_θ(c|z_λ)
pθ(c∣zλ) 赋予正确标签高可能性的数据的概率进行了上加权:可分类良好的数据在知觉质量的Inception评分中得分高,这对生成模型的设计是有益的
设置w > 0,可以提高扩散模型的Inception得分,而代价是样本多样性的降低
对无条件模型应用权重为 w+1 的分类器指导,理论上与对条件模型应用权重为 w 的分类器指导的结果相同,这是因为
p
θ
(
z
λ
∣
c
)
p
θ
(
c
∣
z
λ
)
w
∝
p
θ
(
z
λ
)
p
θ
(
c
∣
z
λ
)
w
+
1
p_θ(z_λ|c)p_θ(c|z_λ)^w ∝ p_θ(z_λ)p_θ(c|z_λ)^{w+1}
pθ(zλ∣c)pθ(c∣zλ)w∝pθ(zλ)pθ(c∣zλ)w+1
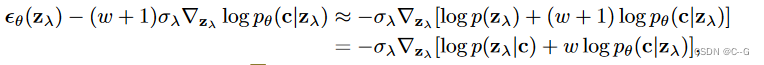
与对无条件模型应用指导相反,当将分类器指导应用于已经有类条件的模型时,获得了最佳结果
CLASSIFIER-FREE GUIDANCE
虽然分类器指导成功地从截断或低温采样中平衡了IS和FID,但它仍然依赖于图像分类器的梯度
而Classifier-free guidance 在没有这种梯度的情况下达到同样的效果,无分类器指导是一种修改
ϵ
θ
(
z
λ
,
c
)
\epsilon_θ(z_λ, c)
ϵθ(zλ,c) 以达到与分类器指导相同效果的替代方法,但**不需要分类器**
没有训练一个单独的分类器模型,而是选择训练一个通过分数估计器
ϵ
θ
(
z
λ
)
\epsilon_θ(z_λ)
ϵθ(zλ) 参数化的 **无条件去噪扩散模型**
p
θ
(
z
)
p_θ(z)
pθ(z),以及通过
ϵ
θ
(
z
λ
,
c
)
\epsilon_θ(z_λ, c)
ϵθ(zλ,c) 参数化的**条件模型**
p
θ
(
z
∣
c
)
p_θ(z|c)
pθ(z∣c)
使用一个神经网络来参数化这两个模型
可以在预测分数时简单地为类别标识符 c 输入一个空令牌 ∅,即
ϵ
θ
(
z
λ
)
=
ϵ
θ
(
z
λ
,
c
=
∅
)
\epsilon_θ(z_λ) = \epsilon_θ(z_λ, c =∅)
ϵθ(zλ)=ϵθ(zλ,c=∅),简单地将 c随机设置为无条件类标识符 ∅,并将其设置为一个超参数,从而共同训练**无条件**和**条件模型**
当然可以训练不同的模型,而不是联合训练它们,但选择联合训练,因为它实现起来非常简单,不会使训练管道复杂化,也不会增加参数的总数
使用以下条件和无条件分数估计的线性组合进行抽样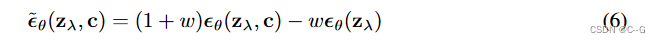
式(6)没有分类器梯度,因此在
ϵ
~
θ
\tilde{\epsilon}_θ
ϵ~θ 方向上迈出一步不能被解释为对图像分类器的基于梯度的对抗性攻击
ϵ
~
θ
\tilde{\epsilon}_θ
ϵ~θ 是由分数估计构造的,由于使用无约束神经网络,这些分数估计是非保守向量场,因此通常不存在一个标量势,例如分类器对数似然,其中
ϵ
~
θ
\tilde{\epsilon}_θ
ϵ~θ 是分类器引导的分数

伪代码如下

实验
使用 log SNR endpoints
λ
m
i
n
=
−
20
λ_{min} = −20
λmin=−20 and $λ_{max} = 20 $,64 × 64和128 × 128类条件ImageNet生成
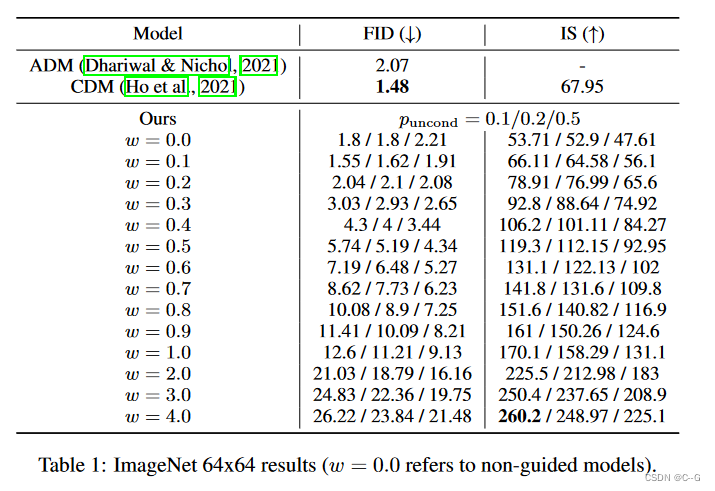
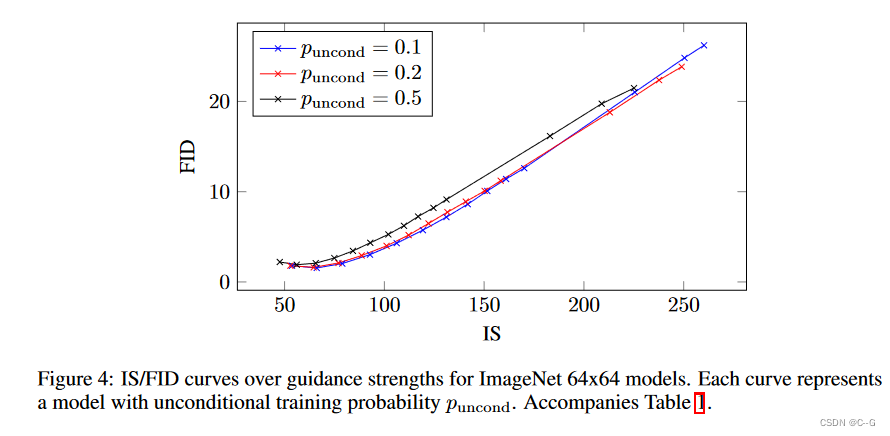
训练时无分类器制导的主要超参数是puncond,即条件扩散模型和无条件扩散模型联合训练时进行无条件生成训练的概率。
在这里,研究了训练模型对64 × 64 ImageNet上不同puncond的影响。
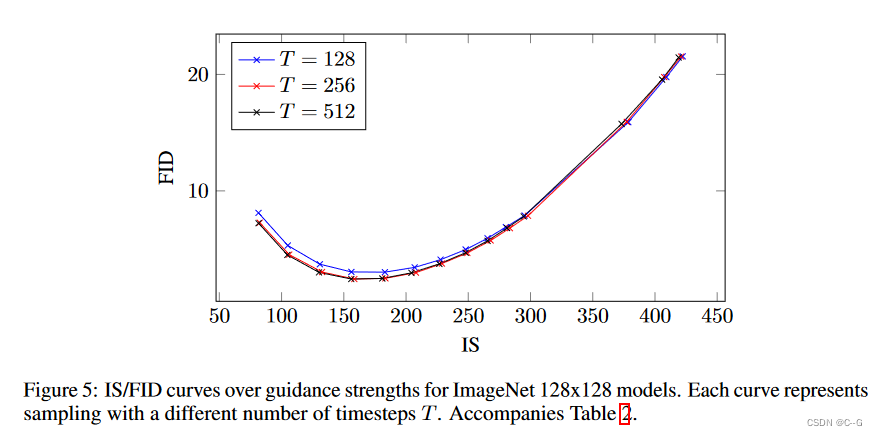
上表和图显示了puncond对样品质量的影响。用puncond∈{0.1,0.2,0.5}训练模型,所有这些都是40万个训练步骤,并在各种指导强度下评估样本质量。发现puncond = 0.5在整个IS/FID边界上始终比puncond∈{0.1,0.2}表现得更差;Puncond∈{0.1,0.2}彼此的性能差不多。
基于这些发现,得出结论,为了产生对样本质量有效的无分类器引导分数,扩散模型的模型容量只需要用于无条件生成任务的相对较小的部分。有趣的是,对于分类器引导,相对较小的分类器和小容量的分类器足以有效地进行分类器引导采样,反映了在无分类器引导模型中发现的这种现象。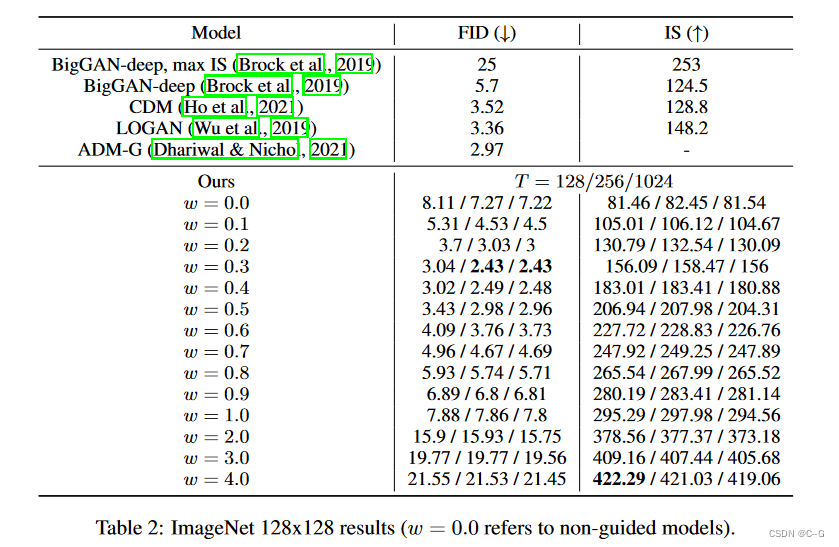
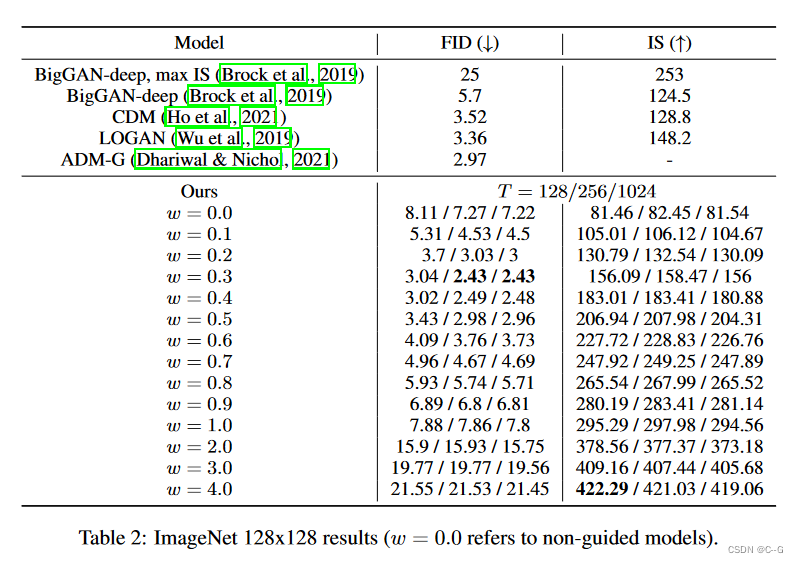
总结
无分类器引导方法最实用的优点是它极其简单:在训练期间只需要一行代码更改(随机删除条件),在采样期间只需要混合条件和无条件分数估计
由于无分类器指导能够像分类器指导一样权衡 is 和 FID,而不需要额外训练的分类器,已经证明了指导可以用纯生成模型执行。此外,扩散模型是由无约束神经网络参数化的,因此与分类器梯度不同,它们的得分估计值不一定形成保守的向量场。因此,无分类器引导采样器遵循完全不类似于分类器梯度的步骤方向,因此不能被解释为对分类器的基于梯度的对抗性攻击,因此结果表明,增强基于分类器的 IS 和 FID 指标可以用纯生成模型完成,该采样过程对使用分类器梯度的图像分类器不具有对抗性。
对于引导的工作原理,也得到了一个直观的解释:它降低了样本的无条件似然,同时增加了条件似然。无分类器引导通过使用负分项降低无条件可能性来实现这一点
无分类器指导依赖于训练无条件模型,但在某些情况下这是可以避免的。如果类分布已知且只有少数类,可以利用
∑
c
p
(
x
∣
c
)
p
(
c
)
=
p
(
x
)
∑_c p(x|c)p(c) = p(x)
∑cp(x∣c)p(c)=p(x) 这一事实从条件分数中获得无条件分数,而无需显式地对无条件分数进行训练。当然,这将需要尽可能多的向前传递,因为有可能的 c 值,并且对于高维条件调节是低效的。
无分类器引导的一个潜在缺点是采样速度。一般来说,分类器可以比生成模型更小和更快,所以分类器引导的采样可能比分类器自由指导更快,因为后者需要运行两个扩散模型的前向传递,一个用于条件评分,另一个用于无条件评分。通过更改架构以在网络的后期注入条件,可以减轻运行扩散模型的多次传递的必要性。
最后,任何以牺牲多样性为代价来提高样本保真度的指导方法都必须面临多样性降低是否可以接受的问题。在部署的模型中可能会有负面影响,因为在应用程序中,某些部分数据在其余数据的上下文中没有得到充分表示,因此维护样本多样性非常重要。
版权归原作者 C--G 所有, 如有侵权,请联系我们删除。