做多了基于机器学习和深度学习的机械故障诊断,感觉实在没意思,换个口味,写一下基于现代信号处理的轴承状态监测和故障诊断。本文主要讲解如何从滚动轴承的振动信号中提取特征、进行状态监测和故障诊断。
完整代码链接如下,面包多第三方下载:
🍞正在为您运送作品详情
首先加载振动信号,该振动信号是由滚动轴承外圈单点缺陷生成的,包含轴承不同运行工况的轴承多段振动信号(缺陷深度从 3um 逐渐增加到 3mm 以上),采样频率为 20 kHz。
导入数据
load data.mat
定义要处理的数据点的数量
numSamples = length(data);
定义采样频率
fs = 20E3; % 单位: Hz
绘制缺陷深度随时间的变化
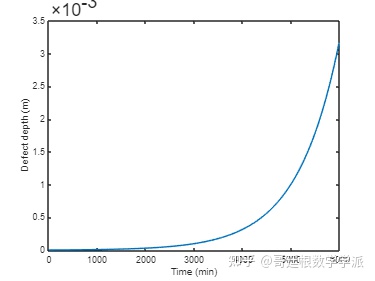
绘制轴承健康数据和故障数据
time = linspace(0,1,fs)';
轴承健康信号
subplot(2,1,1);
plot(time,data{1});
xlabel('Time(s)');
ylabel('Acceleration(m/s^2)');
legend('Healthy bearing signal');
故障轴承信号
subplot(2,1,2);
plot(time,data{end});
xlabel('Time(s)');
ylabel('Acceleration(m/s^2)');
legend('Faulty bearing signal');
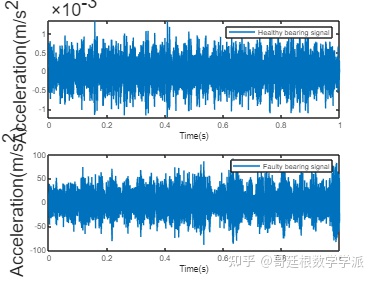
特征提取
从每个数据段中提取代表性特征用于轴承状态监测与故障诊断。 状态监测=的典型特征包括时域特征(均方根、峰值、信号峰度等)或频域特征(峰值频率、平均频率等)。在时域或频域或时-频域中可视化信号有助于发现退化或故障的信号模式。首先计算健康轴承数据的频谱图, 使用 500 个数据点的窗口大小和 90% 的重叠率(相当于 450 个数据点), FFT 的点数设置为 512,fs 表示之前定义的采样频率。
[~,fvec,tvec,P0] = spectrogram(data{1},500,450,512,fs);
fvec 是频率向量,tvec 是时间向量。然后绘制健康轴承信号的时频谱图
clf;
imagesc(tvec,fvec,P0)
xlabel('Time(s)');
ylabel('Frequency(Hz)');
title('Healthy Bearing Signal Spectrogram');
axis xy
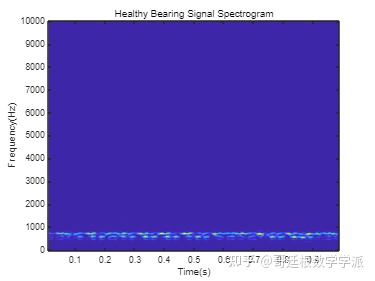
绘制轴承故障振动信号的时频谱图,可以看到信号能量集中在更高的频率。
[~,fvec,tvec,Pfinal] = spectrogram(data{end},500,450,512,fs);
imagesc(tvec,fvec,Pfinal)
xlabel('Time(s)');
ylabel('Frequency(Hz)');
title('Faulty Bearing Signal Spectrogram');
axis xy
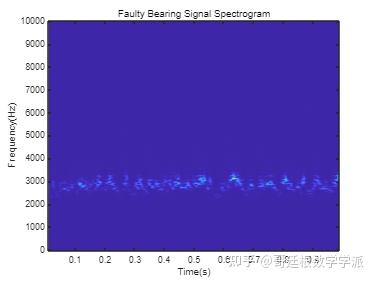
由于健康轴承和故障轴承信号的时频谱图不同,因此可以从频谱图中提取代表性特征并用于状态监测和故障诊断。 在本例中,从时频谱图中提取平均峰值频率作为健康指标。 平均峰值频率即峰值频率的平均值。
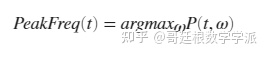
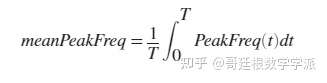
计算健康轴承信号的平均峰值频率
[~,I0] = max(P0); % 找出峰值频率的位置
meanPeakFreq0 = mean(fvec(I0)) % 计算平均峰值频率
meanPeakFreq0 = 666.4602
健康轴承振动信号的平均峰值频率约为 650 Hz,计算故障轴承信号的平均峰值频率。 平均峰值频率移至 2500 Hz 以上。
[~,Ifinal] = max(Pfinal);
meanPeakFreqFinal = mean(fvec(Ifinal))
meanPeakFreqFinal = 2.8068e+03
检查中间阶段的数据,此时缺陷深度不是很大,但已经开始影响振动信号
[~,fvec,tvec,Pmiddle] = spectrogram(data{end/2},500,450,512,fs);
imagesc(tvec,fvec,Pmiddle)
xlabel('Time(s)');
ylabel('Frequency(Hz)');
title('Bearing Signal Spectrogram');
axis xy
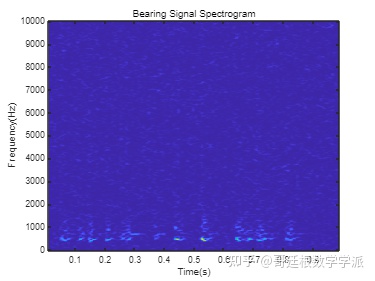
高频噪声分量遍布整个时频谱图,这种现象是原始振动和小缺陷引起的振动的混合效应。 要准确计算平均峰值频率,需要对数据进行滤波以去除那些高频分量。
对振动信号应用中值滤波器以去除高频噪声分量并保留高频中的有用信息,在中值滤波后绘制时频谱图, 高频成分被抑制。
[~,fvec,tvec,Pmiddle] = spectrogram(dataMiddleFilt,500,450,512,fs);
imagesc(tvec,fvec,Pmiddle)
xlabel('Time(s)');
ylabel('Frequency(Hz)');
title('Filtered Bearing Signal Spectrogram');
axis xy
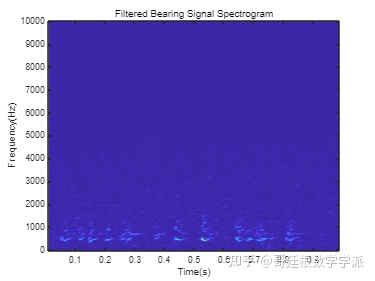
由于平均峰值频率成功地区分健康轴承和故障轴承,因此从每个数据段中提取平均峰值频率。
% 初始化一个向量以存储提取的平均峰值频率
meanPeakFreq = zeros(numSamples,1);
for k = 1:numSamples
% 获取最新数据
curData = data{k};
% 应用中值滤波器
curDataFilt = medfilt1(curData,3);
% 计算spectrogram.
[~,fvec,tvec,P_k] = spectrogram(curDataFilt,500,450,512,fs);
% 计算峰值频率
[~,I] = max(P_k);
meanPeakFreq(k) = mean(fvec(I));
end
绘制提取的平均峰值频率与时间的关系
plot(expTime,meanPeakFreq);
xlabel('Time(min)');
ylabel('Mean peak frequency (Hz)');
grid on;
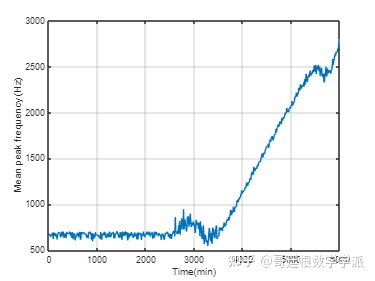
状态监测
使用预定义阈值和动态模型执行状态监测。对于状态监测,如果平均峰值频率超过预定义阈值,则触发警报。将平均峰值频率视为时间序列,则可以估计平均峰值频率的时间序列模型,并使用该模型来预测未来值。使用前 200 个平均峰值频率值创建初始时间序列模型,然后一旦有新值可用,则可以立即更新时间序列模型。这种更新时间序列模型的批处理模式可以捕捉瞬时趋势。本例更新的时间序列模型用于计算提前 10 步的预测。
tStart = 200; % 开始时间
timeSeg = 100; % 建立动态模型的数据长度
forecastLen = 10; % 定义预测时间范围
batchSize = 10; % 定义更新动态模型的批量大小
对于预测和状态监控,需要设置一个阈值来决定何时停止机器运行。 在本例中,使用健康轴承和故障轴承的统计数据来确定阈值。 健康轴承和故障轴承的平均峰值频率的概率分布通过轴承缺陷深度来计算。
绘制健康和故障轴承的平均峰值频率的概率分布
plot(pFreq,pNormal,'g--',pFreq,pFaulty,'r');
xlabel('Mean peak frequency(Hz)');
ylabel('Probability Distribution');
legend('Normal Bearing','Faulty Bearing');
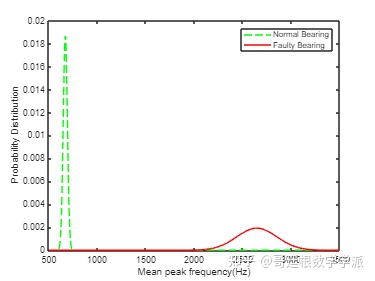
根据上图,将平均峰值频率的阈值设置为 2000Hz,以区分健康轴承和故障轴承
threshold = 2000;
计算采样时间并将其单位转换为秒
samplingTime = 60*(expTime(2)-expTime(1)); % 单位: seconds
tsFeature = iddata(meanPeakFreq(1:tStart),[],samplingTime);
绘制最初的 200 个平均峰值频率数据。
plot(tsFeature.y)
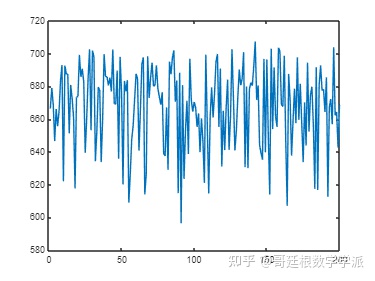
因为最初轴承是健康的,平均峰值频率预计不会显著变化。
使用前 200 个数据点识别二阶状态空间模型, 获取规范形式的模型并指定采样时间。
past_sys = ssest(tsFeature,2,'Ts',samplingTime,'Form','canonical')
past_sys =
Discrete-time identified state-space model:
x(t+Ts) = A x(t) + K e(t)
y(t) = C x(t) + e(t)
A =
x1 x2
x1 0 1
x2 0.9605 0.03942
C =
x1 x2
y1 1 0
K =
y1
x1 -0.003899
x2 0.003656
Sample time: 600 seconds
Parameterization:
CANONICAL form with indices: 2.
Disturbance component: estimate
Number of free coefficients: 4
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on time domain data "tsFeature".
Fit to estimation data: 0.2763% (prediction focus)
FPE: 640, MSE: 602.7
初始估计的动态模型具有低拟合优度, 拟合优度指标是归一化均方根误差 (NRMSE),计算为
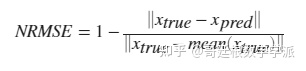
xtrue是真实值,xpred为预测值。当估计数据是恒定电平和噪声的组合时 , NRMSE接近于 0,绘制残差的自相关。
resid(tsFeature,past_sys)
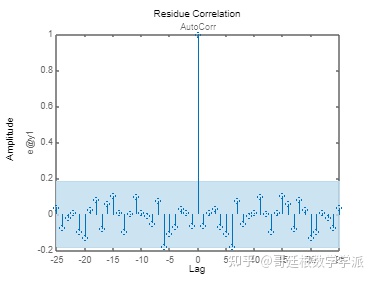
可以看出,残差是不相关的,生成的模型是有效的
使用已识别的模型 past_sys 预测平均峰值频率值并计算预测值的标准偏差。
[yF,~,~,yFSD] = forecast(past_sys,tsFeature,forecastLen);
绘制预测值和置信区间
tHistory = expTime(1:tStart);
forecastTimeIdx = (tStart+1):(tStart+forecastLen);
tForecast = expTime(forecastTimeIdx);
绘制历史数据、预测值和 95% 置信区间。
plot(tHistory,meanPeakFreq(1:tStart),'b',...
tForecast,yF.OutputData,'kx',...
[tHistory; tForecast], threshold*ones(1,length(tHistory)+forecastLen), 'r--',...
tForecast,yF.OutputData+1.96*yFSD,'g--',...
tForecast,yF.OutputData-1.96*yFSD,'g--');
ylim([400, 1.1*threshold]);
ylabel('Mean peak frequency (Hz)');
xlabel('Time (min)');
legend({'Past Data', 'Forecast', 'Failure Threshold', '95% C.I'},...
'Location','northoutside','Orientation','horizontal');
grid on;
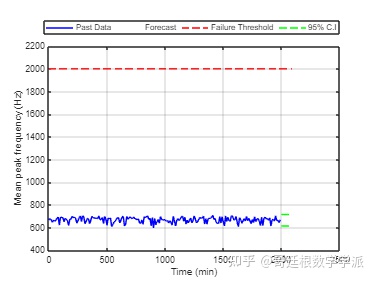
该图显示平均峰值频率的预测值远低于阈值。
随着新数据的到来更新模型参数,并重新估计预测值。 创建警报以检查信号或预测值是否超过故障阈值。
for tCur = tStart:batchSize:numSamples
tsFeature = iddata(meanPeakFreq((tCur-timeSeg+1):tCur),[],samplingTime);
% 当新数据进来时更新系统参数
% parameters as initial guesses.
sys = ssest(tsFeature,past_sys);
past_sys = sys;
% 预测更新后的状态空间模型的输出
[yF,~,~,yFSD] = forecast(sys, tsFeature, forecastLen);
% 查找与历史数据和预测值对应的时间
tHistory = expTime(1:tCur);
forecastTimeIdx = (tCur+1):(tCur+forecastLen);
tForecast = expTime(forecastTimeIdx);
% 绘制历史数据、预测的平均峰值频率值和 95%置信区间
plot(tHistory,meanPeakFreq(1:tCur),'b',...
tForecast,yF.OutputData,'kx',...
[tHistory; tForecast], threshold*ones(1,length(tHistory)+forecastLen), 'r--',...
tForecast,yF.OutputData+1.96*yFSD,'g--',...
tForecast,yF.OutputData-1.96*yFSD,'g--');
ylim([400, 1.1*threshold]);
ylabel('Mean peak frequency (Hz)');
xlabel('Time (min)');
legend({'Past Data', 'Forecast', 'Failure Threshold', '95% C.I'},...
'Location','northoutside','Orientation','horizontal');
grid on;
% 当实际监控变量或预测值超过故障阈值时显示警报
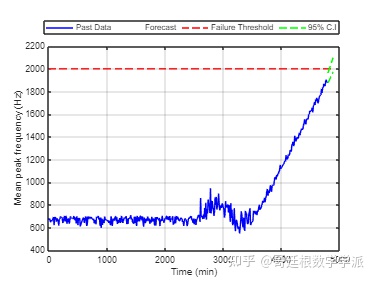
if(any(meanPeakFreq(tCur-batchSize+1:tCur)>threshold))
disp('Monitored variable exceeds failure threshold');
break;
elseif(any(yF.y>threshold))
% 估计系统达到故障阈值的时间
tAlarm = tForecast(find(yF.y>threshold,1));
disp(['Estimated to hit failure threshold in ' num2str(tAlarm-tHistory(end)) ' minutes from now.']);
break;
end
end
版权归原作者 哥廷根数学学派 所有, 如有侵权,请联系我们删除。