Transformer是什么呢？
\qquad
Transformer最早起源于论文Attention is all your need，是谷歌云TPU推荐的参考模型。
\qquad
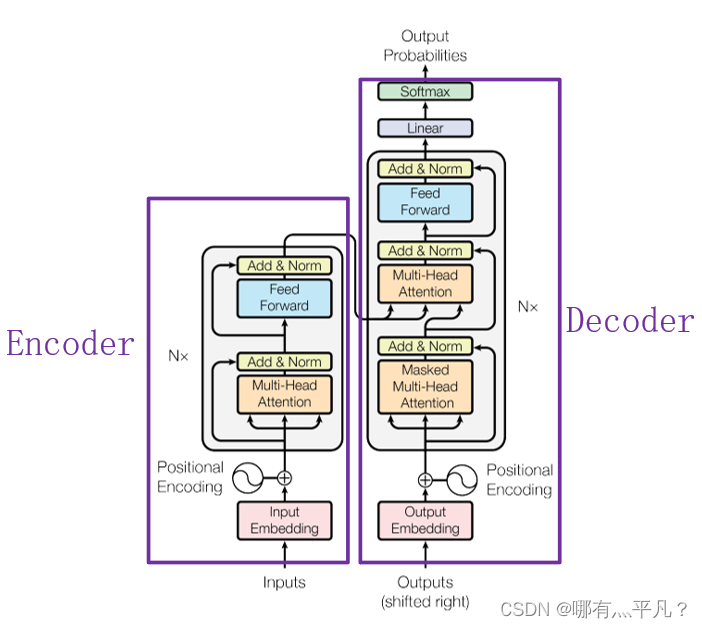
目前，在NLP领域当中，主要存在三种特征处理器——CNN、RNN以及Transformer，当前Transformer的流行程度已经大过CNN和RNN，它抛弃了传统CNN和RNN神经网络，整个网络结构完全由Attention机制以及前馈神经网络组成。首先给出一个来自原论文的Transformer整体架构图方便之后回顾。
\qquad
上图中的Transformer可以说是一个使用“self attention”的Seq2seq模型。
那么要想了解Transformer，就必须先了解"self attention"。
\qquad
如果给出一个Sequence要处理，最常想到的可能就是RNN了，如下图1所示。RNN被经常使用在输入是有序列信息的模型中，但它也存在一个问题——它不容易被“平行化”。那么“平行化”是什么呢？
\qquad
比如说在RNN中a1,a2,a3,a4就是输入，b1,b2,b3,b4就是输出。对于单向RNN，如果你要输出b3那么你需要把a1,a2,a3都输入并运算了才能得到；对于双向RNN，如果你要输出任何一个bi,那么你要把所有的ai都输入并运算过才能得到。它们无法同时进行运算得出b1,b2,b3,b4。
\qquad
而针对RNN无法“平行化”这个问题，有人提出了使用CNN来取代RNN，如下图所示。输入输出依然为ai、bi。它利用一个个Filter（如下图黄色三角形）（我的理解是类似于计网的滑动窗口协议）去得出相应的输出，比如b1是通过a1,a2一起得出；b2是通过a1,a2,a3得出。可能会存在一个疑问——这样不就只考虑临近输入的信息，而对长距离信息没有考虑了？
\qquad
当然不是这样，它可以考虑长距离信息的输入，只需要在输出bi上再叠加一层Filters就能涵盖更多的信息，如下图黄色三角形，所有输入ai运算得出b1,b2,b3作为该层的输入。所以说只要你叠加的层数够多，它可以包含你所有的输入信息。
\qquad
回到咱们对“平行化”问题的解答：使用CNN是可以做到“平行化”的，下图中每一个蓝色的三角形，并不用等前面的三角形执行完才能执行，它们可以同时进行运算。
self attention
\qquad
self attention模型输入的xi先做embedding得到ai，每一个xi都分别乘上三个不同的w得到q、k、v。
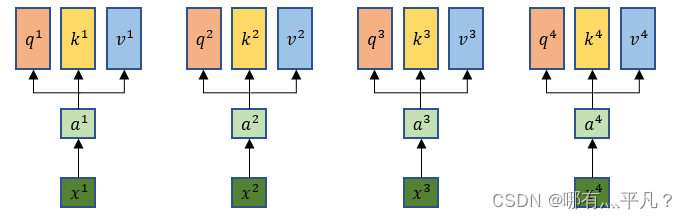
其中：
\qquad
\qquad
\qquad
\qquad
a
i
=
W
x
i
\ a^i=Wx^i
ai=Wxi
\qquad
\qquad
\qquad
\qquad
\qquad
q
i
=
W
q
a
i
\ q^i=W^qa^i
qi=Wqai
\qquad
\qquad
\qquad
\qquad
\qquad
k
i
=
W
k
a
i
\ k^i=W^ka^i
ki=Wkai
\qquad
\qquad
\qquad
\qquad
\qquad
v
i
=
W
v
a
i
\ v^i=W^va^i
vi=Wvai
拿每个qi去对每个ki做点积得到
a
1
,
i
\ a_{1,i}
a1,i，其中d是q和k的维度。
\qquad
\qquad
\qquad
\qquad
\qquad
a
1
,
i
=
q
1
⋅
k
i
/
d
\ a_{1,i}=q^1·k^i/{\sqrt d}
a1,i=q1⋅ki/d
再把
a
1
,
i
\ a_{1,i}
a1,i经过一个Soft-max之后得到
a
^
1
,
i
\hat a_{1,i}
a^1,i
a
^
1
,
i
=
e
x
p
(
a
1
,
i
)
/
∑
j
e
x
p
(
a
1
,
j
)
\hat a_{1,i} =exp(a_{1,i})/\sum_{j} exp(a_{1,j})
a^1,i=exp(a1,i)/j∑exp(a1,j)
\qquad
接下来把
a
^
1
,
j
\hat a_{1,j}
a^1,j与对应的
v
j
v^j
vj分别做乘积最后求和得出第一个输出
b
1
b_1
b1，同理可得到所有
b
i
b_i
bi。
b
1
=
∑
i
n
a
^
1
,
i
v
i
b^1 =\sum_{i}^n \hat a_{1,i}v^i
b1=i∑na^1,ivi
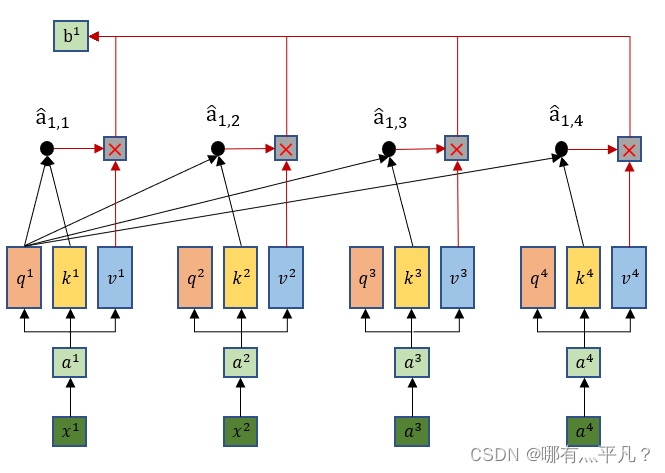
\qquad
那么到这里就可以看出输出b1是综合了所有的输入xi信息，同时这样做的优势在于——当b1只需要考虑局部信息的时候（比如重点关注x1,x2就行了），那么它可以让
a
^
1
,
3
\hat a_{1,3}
a^1,3和
a
^
1
,
4
\hat a_{1,4}
a^1,4输出的值为0就行了。
那么self attention是这么做平行化的呢？
咱们复习一下前面说到的q、k、v的计算：
\qquad
\qquad
\qquad
\qquad
\qquad
q
i
=
W
q
a
i
\ q^i=W^qa^i
qi=Wqai
\qquad
\qquad
\qquad
\qquad
\qquad
k
i
=
W
k
a
i
\ k^i=W^ka^i
ki=Wkai
\qquad
\qquad
\qquad
\qquad
\qquad
v
i
=
W
v
a
i
\ v^i=W^va^i
vi=Wvai
\qquad
因为
q
1
=
w
q
a
1
\ q^1=w^qa^1
q1=wqa1，那么根据矩阵运算原理，我们将
a
1
、
a
2
、
a
3
、
a
4
\ a^1、a^2、a^3、a^4
a1、a2、a3、a4串起来作为一个矩阵I与
w
q
\ w^q
wq相乘可以得到
q
1
、
q
2
、
q
3
、
q
4
\ q^1、q^2、q^3、q^4
q1、q2、q3、q4构成的矩阵Q。同理可得
k
i
、
v
i
\ k^i、v^i
ki、vi的矩阵K、V。
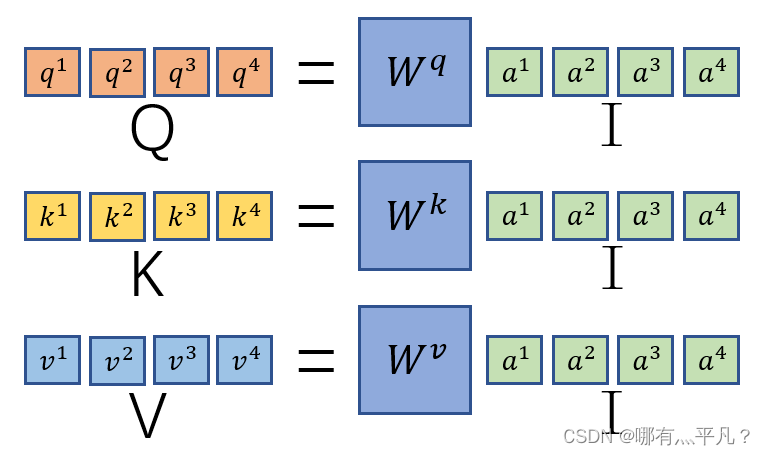
然后我们再回忆观察一下
a
1
,
i
\ a_{1,i}
a1,i的计算过程(为方便理解，此处省略
d
\sqrt d
d)：
\qquad
\qquad
\qquad
a
1
,
1
=
k
1
⋅
q
1
\ a_{1,1}=k^1·q^1
a1,1=k1⋅q1
\qquad
a
1
,
2
=
k
2
⋅
q
1
\ a_{1,2}=k^2·q^1
a1,2=k2⋅q1
\qquad
\qquad
\qquad
a
1
,
3
=
k
3
⋅
q
1
\ a_{1,3}=k^3·q^1
a1,3=k3⋅q1
\qquad
a
1
,
4
=
k
4
⋅
q
1
\ a_{1,4}=k^4·q^1
a1,4=k4⋅q1
\qquad
我们可以发现计算都是用
q
1
\ q^1
q1去乘以每个
k
i
\ k^i
ki得出
a
1
,
i
\ a_{1,i}
a1,i，那么我们将
k
i
\ k^i
ki叠加起来与
q
1
\ q^1
q1相乘得到一列向量
a
1
,
i
\ a_{1,i}
a1,i(i=1,2,3,4)。然后你再加上所有的
q
i
\ q^i
qi就可以得到整个
a
i
,
j
\ a_{i,j}
ai,j矩阵。最后对
a
i
,
j
\ a_{i,j}
ai,j的每一列做一个soft-max就得到
a
^
i
,
j
\hat a_{i,j}
a^i,j矩阵。
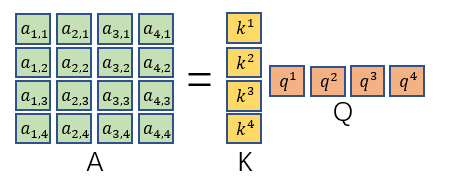
最后再把
a
^
i
,
j
\hat a_{i,j}
a^i,j与所有
v
i
\ v^i
vi构成的矩阵V相乘即可得到输出。
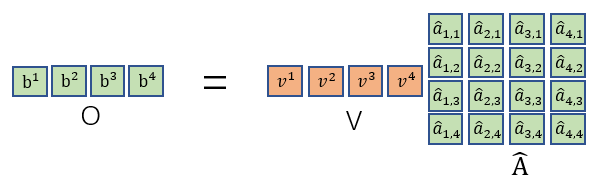
\qquad
在这里我们对输入I到输出O之间做的事情做一个总结：我们先用I分别乘上对应的
W
i
\ W^i
Wi得到矩阵Q,K,V，再把Q与
K
T
\ K^T
KT相乘得到矩阵A，再对A做soft-max处理得到矩阵KaTeX parse error: Expected group after '^' at position 7: \hat A^̲，最后再将KaTeX parse error: Expected group after '^' at position 7: \hat A^̲与V相乘得到输出结果O。整个过程都是进行矩阵乘法，都可以使用GPU加速。
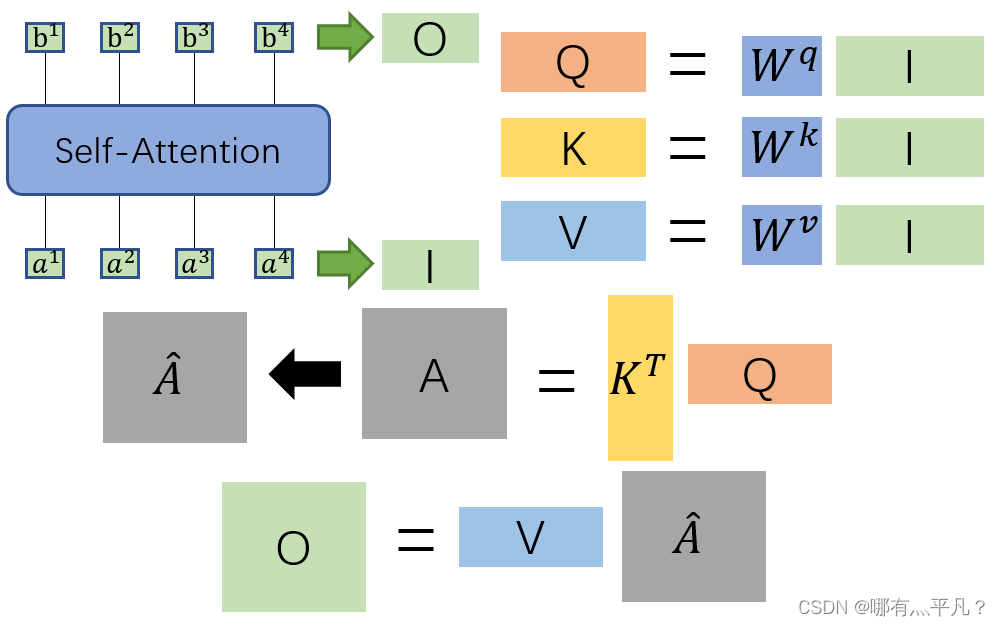
self-attention的变形——Multi-head Self-attention
\qquad
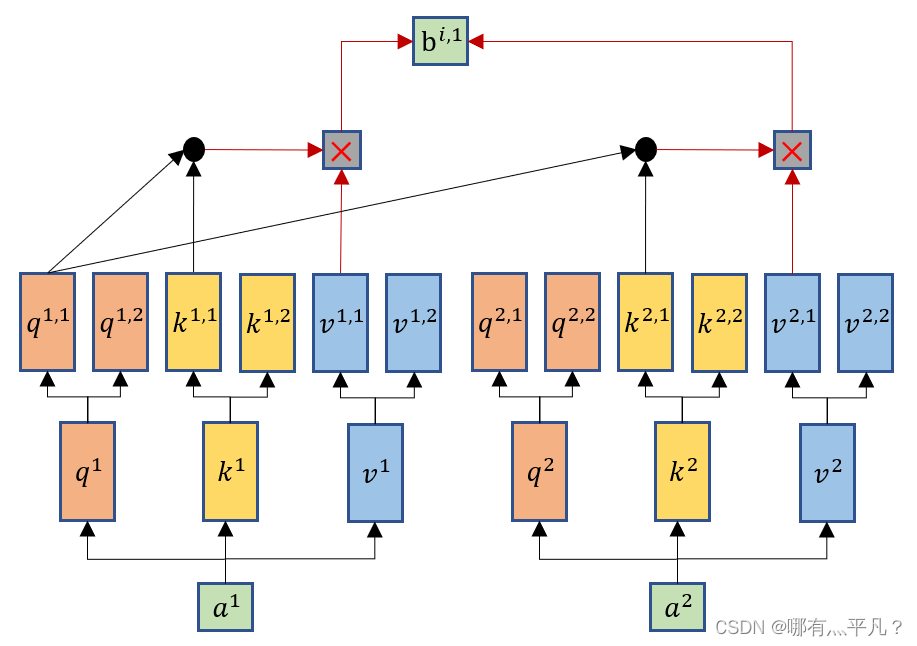
Multi-head Self-attention跟self-attention一样都会生成q、k、v，但是Multi-head Self-attention会再将q、k、v分裂出多个
q
1
,
2
\ q^{1,2}
q1,2（这里举例分裂成两个），然后它也将q跟k去进行相乘计算，但是只跟其对应的k、v进行计算，比如
q
1
,
1
\ q^{1,1}
q1,1只会与
k
1
,
1
\ k^{1,1}
k1,1、
k
2
,
1
\ k^{2,1}
k2,1进行运算，然后一样的乘以对应的v得到输出
b
1
,
1
\ b^{1,1}
b1,1。
\qquad
\qquad
\qquad
q
1
,
1
=
W
q
,
1
q
1
\ q^{1,1}=W^{q,1}q^1
q1,1=Wq,1q1
\qquad
\qquad
q
1
,
2
=
W
q
,
2
q
1
\ q^{1,2}=W^{q,2}q^1
q1,2=Wq,2q1
\qquad
对于
b
i
,
1
\ b^{i,1}
bi,1再进行一步处理就得到我们在self-attention所做的一步骤的输出
b
i
\ b^i
bi。
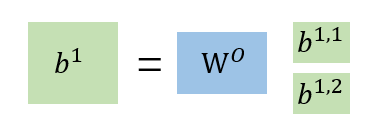
那么这个Multi-head Self-attention设置多个q,k,v有什么好处呢？
\qquad
举例来说，有可能不同的head关注的点不一样，有一些head可能只关注局部的信息，有一些head可能想要关注全局的信息，有了多头注意里机制后，每个head可以各司其职去做自己想做的事情。
Positional Encoding
\qquad
根据前面self-attention介绍中，我们可以知道其中的运算是没有去考虑位置信息，而我们希望是把输入序列每个元素的位置信息考虑进去，那么就要在
a
i
\ a^i
ai这一步还有加上一个位置信息向量
e
i
\ e^i
ei，每个
e
i
\ e^i
ei都是其对应位置的独特向量。——
e
i
\ e^i
ei是通过人工手设（不是学习出来的）。
最后挂上一张来自原论文的效果图，体验一下transformer的强大：
本文转载自: https://blog.csdn.net/m0_67505927/article/details/123209347
版权归原作者 哪有灬平凡？ 所有， 如有侵权，请联系我们删除。
版权归原作者 哪有灬平凡？ 所有， 如有侵权，请联系我们删除。