520不要老想着谈恋爱要变的更加爱强化学习

强化学习简介

监督学习：传统的机械学习都是属于监督监督学习，监督学习在训练模型的过程中通过目标值给与智能体预测的值来对比从而判断是否正确，从而引导智能体做出正确的行为。
强化学习：不同于监督学习，强化学习在训练智能体时会考虑自己下一步的动作怎么做才
会使奖励或者报酬最大化。常用的基于策略或者基于值得算法。
所以相较于监督学习强化学习的学习能力更强，他可以在无数次的训练中自己探索出最优
解，这是当下人工智能最吸引人的地方。

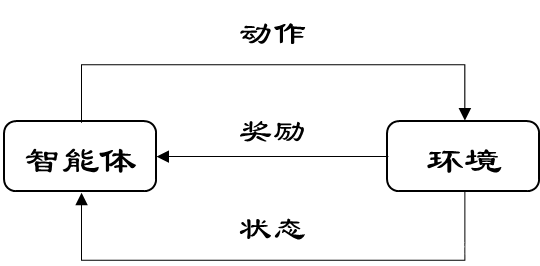
学习过程

强化学习可以用四元组<S,A,P,R>表示，其中S为状态集合、A为动作集合、P为状态转移函数、R为奖励函数，其计算流程如下：
（1）在时刻t，智能体所处状态s t∈S，此时需要一定的策略policy从动作集合中选择下一个动作a t∈A。动作的连续性和集合的大小将会影响到后面的结果。
（2）在完成动作at后,环境会给出一个强化信号r t（奖励或者惩罚）。r t=R(s t,a t,s t+1)其中St∈S是状态，S是状态空间，a t ∈A是动作 A是动作空间。
（3）动作a t同时会改变环境。从当前转台s t转移到下一个状态St+1选择下一个动作，进入下一个动作的迭代。
​ **​

基于策略的算法和基于值的算法**

基于值函数的强化学习方法
基于模型的动态规划方法：
这是基于模型的强化学习算法，也就是说都是已知的。为什么可以用动态规划来求解强化学习的最优策略，是因为动态规划问题的最优解可通过寻找子问题的最优解来得到问题的最优解。并且可以找到子问题状态之间的递推关系，通过较小的子问题状态递推出较大的子问题的状态。而强化学习的问题恰好是满足这两个条件的，下面是强化学习值函数的贝尔曼方程：
(1)由上式可求解每个状态的状态价值函数，这个式子又是一个递推的式子,我们可以使用上一个迭代周期内的状态价值来计算更新当前迭代周期某状态的状态价值。基于模型的动态规划算法分为两步，首先是评估当前策略，就是求出当前策略下每个状态的价值, 策略评估的基本思路是从任意一个状态价值函数开始，依据给定的策略，结合贝尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数，直至其收敛，即,得到该策略下最终的状态价值函数。第k次的值函数计算可用下面的式子：
(2)第二步：策略改善，通过第一步的策略评估我们得到了当前策略的各个状态的，就可以根据对当前策略进行改善。可以使用贪婪策略来对当前策略进行改善。将策略评估和策略改善组合起来就是策略迭代算法，在策略评估中，给定策略，通过数值迭代算法不断计算每个状态的值函数，利用该值函数和贪婪策略得到新的策略，重复循环策略评估和改进，最终会得到最优策略。
基于蒙特卡罗的强化学习算法
这是无模型的强化学习方法，在无模型的强化学习中，状态转移概率未知，所以不能够使用贝尔曼方程对策略进行评估，可以根据值函数本身的定义来评估策略，下面的式子是值函数的定义式：
（1）值函数的计算实际上就是计算期望，在没有模型时，可以采用蒙特卡罗方法计算期望，就是利用样本估计期望。蒙特卡罗法通过采样若干经历完整的状态序列来估计状态的真实价值。所谓的经历完整，就是这个序列必须是达到终点的，也称试验。计算一次试验中状态s处的折扣回报值为：对于蒙特卡罗法来说，如果要求某一个状态的状态值，只需要求出所有的完整序列中该状态出现时的收获再取平均值即可近似求解，也就是：
(2)其中表示第一次试验中，第一次出现状态时计算处折扣回报。利用(2)式求均值比较麻烦，可以改成增量的形式：上面的策略评估，策略改进一般使用策略，为了使算法可以收敛，一般会随着算法的迭代过程逐渐减小，并趋于0。基于蒙特卡罗的算法流程：输入:状态集, 动作集, 即时奖励，衰减因子, 探索率过程:
1: 初始化所有的动作价， 状态次数，采样次数，初始化一个策略，等概率选取当前状态下，能够选择的动作。
2: , 基于策略进行第 次蒙特卡罗采样，得到一次试验
3:对于试验中出现的每一状态行为对,更新，
4: 基于新计算出的动作价值，更新当前的贪婪策略
5:如果所有的值都收敛了，(判断收敛的标准就是所有的值与上一次迭代的值的误差为，)，那么就得到最优策略，否则继续重复
输出:最优策略
时间差分法（和）时间差分法和蒙特卡罗都是无模型的强化学习算法，它俩的不同在于值函数的估计，蒙特卡罗是通过采样完整的一次试验计算平均值来更新策略，而时间差分法结合了蒙特卡罗的采样和动态规划中的自举，使用了贝尔曼方程：
（1）可以在每次采样中利用当前的及时回报以及来代替蒙特卡罗中的，即可以得到时间差分的值函数公式
（2）蒙特卡罗方法中的返回值，其期望就是值函数的定义，所以是无偏估计，但是每次得到，要等到最终状态，中间会经历很多随机状态和动作，所以的随机性大，方差大。而时间差分不用等到最终状态，它可以走一步更新一次，TD目标中是估计值，所以方法是有偏估计，次只用了一步的随机状态和动作，所以方差小。时间差分法中同策略的方法：同策略就是采样的策略和评估、改进的策略是同一个策略。
算法流程：
输入:迭代轮数，状态集, 动作集, 步长，衰减因子, 探索率过程:
1:随机初始化所有的状态和动作对应的价值。
2:，进行迭代。初始化,为当前状态序列的第一个状态。设置为贪婪法在当前状态选择的动作。在状态执行当前动作,得到新状态和奖励，用贪婪法在状态选择新的动作更新价值函数:如果是终止状态，当前轮迭代完毕，否则转到步骤输出:所有的状态和动作对应的价值在步中，只是用贪婪法选取了下一个状态的下一个动作，实际上并不会执行，只是为了在中计算。
时间差分法中异策略的方法: 。异策略就是采样的策略和评估改进的策略不是同一个策略。这里说一下同策略和异策略的比较：同策略就是采样的策略和我们想要学习的策略一致，在异策略学习中，想要学习的是一个策略，而实际用于采样的又是另外一个策略。采取异策略的优点有：可以从给出的示教样本或其他智能体给出的引导样本中学习；可以重用由旧策略生成的数据；可以用一个策略进行采样，然后同时学习多个策略；可以在使用一个探索性策略的同时学习一个确定性策略。就是这样的，使用探索的策略采样数据，去学习一个确定的策略。
算法流程：
输入:迭代轮数, 动作集, 步长，衰减因子, 探索率
过程:
1 随机初始化所有的状态和动作对应的价值。
2 ，进行迭代。
初始化为当前状态序列的第一个状态。用贪婪法在当前状态选择出动作在状态执行当前动作,得到新状态和奖励更新价值函数:如果是终止状态，当前轮迭代完毕，否则转到步骤输出：所有的状态和动作对应的价值的目标函数中的动作是由贪婪策略得到的，对于，我们会使用贪婪法来选择新的动作，这部分和完全相同。但是对于价值函数的更新，使用的是贪婪法，而不是完的贪婪法。这一点就是和本质的区别。
DQN算法
前面的方法都是针对状态和动作空间都是离散的，所以可以用表格记录下来。而当状态维度很大或者连续时，不可能一一列出值，这时就要使用一个函数逼近的方法来表示值。
函数逼近可以使用非线性参数逼近比如神经网络，可以将逼近的值函数写为,其中就是神经网络的参数。
从蒙特卡罗和时间差分的值函数更新公式可以看出，值函数的更新过程就是向着目标值函数靠近的过程，函数逼近就是一个监督学习的过程，它的训练目标函数为：。前面是目标值函数（一次试验中实际计算得到的），后面是值函数逼近得到的，也就是根据值函数的神经网络计算得到的。
就是神经网络的值函数逼近和的结合,它相比于改进了以下3点：
(1)利⽤深度神经⽹络逼近值函数
(2)利⽤了经验回放训练强化学习的学习过程
(3)独⽴设置了⽬标⽹络来单独处理时间差分算法中的偏差
经验回放：将试验得到的历史数据存放在一起，然后等概率的采样集合，作为输入，训练神经网络。可以打破数据之间的关联性。
DQN的目标函数为：，其中目标，计算目标的网络和要逼近的网络如果是同一个网络容易导致数据之间有很强的关联性，训练不稳定。所以就将两个网络设置成一样的结构,但参数不同的神经网络，实际中目标网络的更新可以通过硬更新，当逼近的网络更新了次，直接将逼近的网络参数赋值给目标网络的参数。
基于策略的强化学习算法
策略梯度算法
将策略参数化，即由变为，一般使用非线性函数（神经网络）表示，寻找神经网络的最优参数使得目标函数最大，强化学习的最终目标就是使得累积回报的期望最大：。
在基于值函数的⽅法中，迭代计算的是值函数，再根据值函数改善策略；⽽在基于策略的⽅法中，我们直接对策略进⾏迭代计算，也就是迭代更新策略的参数值，直到累积回报的期望最⼤，此时的参数所对应的策略为最优策略。
基于策略相比于值函数的优点：直接策略搜索⽅法是对策略进⾏参数化表⽰，基于策略的方法适用于动作空间很大或者是连续的情况；基于策略的方法一般使用随机策略，直接将随机策略集成到所学的策略中。
基于策略方法的缺点：容易收敛到局部最优；评估单个策略时并不充分，方差较大。
策略梯度算法的推导：
首先用表示一次试验的轨迹：。表示轨迹的累积回报。表示轨迹出现的概率。强化学习的目标是累积回报的期望最大，这时就是一个 最优化问题，就是求一组，使得最大，可以使用梯度提升。计算策略梯度,对式求导 最终策略梯度变成了求值的期望，可以使用经验平均值估计期望。根据当前策略，采样条轨迹，计算这条轨迹的平均值：
求解，由于，所以：其中是环境动力学，且没有参数，可以忽略，它是无偏的，方差很大，可以引入一个基线。来分析一下引入基线的好处，如果所有的回报都是正的，那么所有轨迹出现的概率都会增加。一个比较好的动作没有被采样到，而采样到的不好的动作得到了一个比较小的正的回报，那么没有被采样到的好动作的出现概率会越来越小，这显然是不合适的。因此需要增加一个回报的基线，让回报有正有负。比如对于一些状态来说，他们都具有比较大的动作值函数。那么我们就需要有一个大的基线来区分更大的动作值和相对小的动作值。但是对于其他一些状态，所有状态的值函数都比较小，那么我们就需要一个小的基线值。这个基线可以选择状态值函数的估计值，相当于动作状态值函数的一个平均值。
基于值函数和策略的方法
算法
该算法从名字上看包含了两部分：其中就是策略函数，可以用来生成动作和环境互动，是价值评估，用来评价的表现。该算法可以看成是策略梯度和的结合，它包含了两个近似：策略函数的近似和值函数的近似：策略函数的近似，值函数的近似，算法就是对蒙特卡罗策略梯度的改进，在蒙特卡罗策略梯度算法中，算法改变的就是，原来的蒙特卡罗策略梯度算法中，是一次试验完成后计算的t步开始的累积奖励，这就会带来不便，每次只能等到试验结束才能更新，而且随机性大，方差高。算法改进了，它是使用部分得到的，即值函数的近似来计算得到的，就像一样。网络的更新公式同，网络的更新公式同策略梯度算法，它的形式可以有多种，见下：其中，补充一下，策略网络输出的东西是什么：动作是离散的，就可以使用输出每个动作的概率值；动作是连续的，就可以输出策略分布的参数(常见使用高斯分布，输出。
**:
近端策略优化
**这种算法用在强化学习中的表现能达到甚至超过现有算法的顶尖水平，同时还更易于实现和调试。所以 已经把作为自己强化学习研究中首选的算法。近端策略优化，具有信任区域策略优化的一些优点，但它实现起来更简单，更通用，并且具有更好的样本复杂性（根据经验）。合理性的理论实际上建议使用惩罚而不是约束，即解决无约束优化问题：对两个分布的距离施加一个惩罚。把两个分布的距离惩罚直接换成了，压缩到一个范围内。
参考文献
[1]深入浅出强化学习，郭宪
[2]博客园 刘建平
[3知乎 rootxuan