时间序列的数据分析(六):指数平滑预测法

之前已经完成了五篇关于时间序列的博客，还没有阅读过的读者请先阅读：

时间序列的数据分析(一):主要成分
时间序列的数据分析(二):数据趋势的计算
时间序列的数据分析(三):经典时间序列分解
时间序列的数据分析(四):STL分解
时间序列的数据分析(五):简单预测法

指数平滑是在20世纪50年代后期提出的预测方法(Brown, 1959; Holt, 1957; Winters, 1960)，其原理是使用指数平滑方法生成的预测值是过去观测值的加权平均值，并且随着过去观测值离预测值距离的增大，权重呈指数型衰减。换句话说，观察值越近，相应的权重越高。

一.简单指数平滑预测(Brown)

最简单的指数平滑方法被称为“简单指数平滑”，这种方法适用于预测没有明显趋势或季节特征的数据。简单指数平滑通过一个递归式来获取所有观测数据的权重,并在此基础上做出对未来的预测。简单指数平滑的递归式定义：

$S_t = \alpha X_t + (1-\alpha) S_{t-1} \quad \text{where} \quad \alpha \in (0,1)$

如果我们将上面的递归式展开可以得到如下的等式：

$S_t = \alpha X_t + (1-\alpha) S_{t-1}\\\\= \alpha X_t + \alpha(1-\alpha) X_{t-1} + \alpha(1-\alpha)^2 X_{t-2}+\cdots+ \alpha(1-\alpha)^{t-1} X_1+ (1-\alpha)^tS_0$

最后我们将此递归展开式进行整理后得到：

$S_t = \sum_{i=0}^{t-1} \alpha(1-\alpha)^i X_{t-i} + (1-\alpha)^tS_0$

** 预测公式：**

$\hat{X}_{t+h} = S_t = \sum_{i=0}^{t-1} \alpha(1-\alpha)^i X_{t-i} + (1-\alpha)^tS_0 \quad \text{where} \quad h=1,2,3\cdots$

其中

$S_t$ ：表示t+h 时刻的预测值即 $\hat{X}_{t+h} = S_t \quad \text{where} \quad h=1,2,3\cdots$
$X_t$ : 表示时刻 t 的实际观测值.
$\alpha:$ 是平滑参数 $0 \le \alpha \le 1$
$S_0:$ : 它是递归展开式的初始化参数。

这里可以将 $S_0$ 理解为 $X_1$ 的预测值即 $\hat{X}_1$ ， $S_1$ 为 $X_2$ 的预测值即 $\hat{X}_2$ ,以此类推。而 $S_t$ 表示未来t+h时刻的预测值，这里的 $t$ 表示数据中的最后一个时刻, 因为我们需要同时预测多个未来值所以 h可以表示1,2,3...等多个未来预测值，只不过我们用简单平滑方法预测的所有的未来值都是相同的。

指数平滑方法会将更大的权重赋到最近的观测值，对于更久远的观测值则会赋予较小的权重，权重的衰减速度由参数 $\alpha$ 控制。这里权重 $\alpha , \alpha(1-\alpha), \alpha(1-\alpha)^2 ,\alpha(1-\alpha)^3 \cdots$ 会以指数方式逐渐衰减到0，下面我们我们对 $\alpha$ 取值0.2,0.4,0.6,0.8,1来观察权重的衰减过程：

size=10
df_alpha=pd.DataFrame()
df_alpha.index=['α(1-α)^'+str(i) for i in range(size)]
df_alpha['alpha=0.2']=[.2*((1-.2)**i) for i in range(size)]
df_alpha['alpha=0.4']=[.4*((1-.4)**i) for i in range(size)]
df_alpha['alpha=0.6']=[.6*((1-.6)**i) for i in range(size)]
df_alpha['alpha=0.8']=[.8*((1-.8)**i) for i in range(size)]
df_alpha['alpha=1']=[1*((1-1)**i) for i in range(size)]
df_alpha.reset_index().iloc[:,1:].plot();

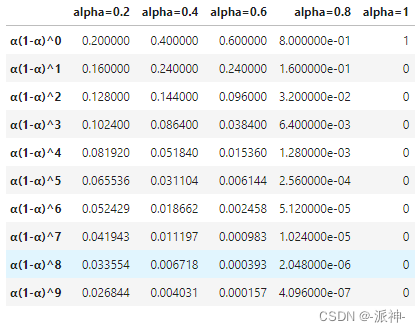
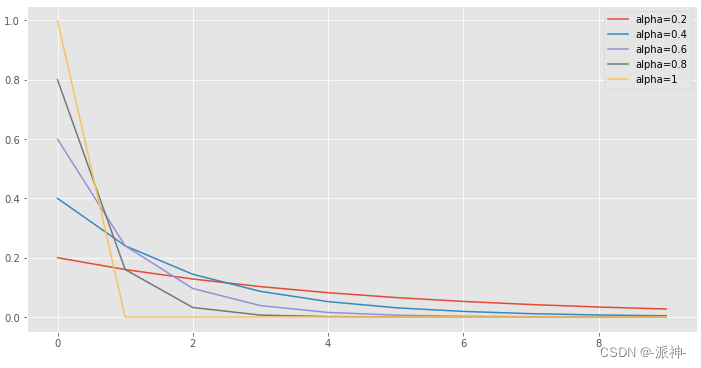
对于0到1之间的任何 $\alpha$ 值，随着时间向前推移，观察值的权重呈指数型下降，因此我们称之为“指数平滑”。当 $\alpha$ 越大时权重衰减的越快。当 $\alpha$ 越小时权重衰减的越慢，当 $\alpha=1$ , $\hat{X}_{t+1}=X_t$ 的极端情况，指数平滑的预测值等于最后一个预测值。

$\alpha$ 与 $S_0$ 的选择：

对于 $\alpha$ 我们可以通过对过去时刻的预测值与实际值进行比较来挑选预测误差最小时的 $\alpha$ 值，我们可以使用SSE(误差平方和)、 MAPE（平均绝对百分比误差）、MSE（均方误差）或 RMSE（均方根误差）等指标来评估预测误差，并且选择最合适的 $\alpha$ 值以使误差最小。通常可以使用 SSE 作为选择适当平滑常数的标准。例如，通过分配从 0.1 到 0.99 的值，我们选择产生最小 SSE 的值的 $\alpha$ ,SSE的定义如下：

$\text{SSE}=\sum_{t=1}^T(X_t - \hat{X}_{t})^2=\sum_{t=1}^Te_t^2$

其中：

这里, $t=1,2\dots,T$ 。设定残差为 $e_t=X_t - \hat{X}_t$ 。

对于 $S_0$ 我们可以有两种选择方法：

选取第一个时刻的实际值作为 $S_0$ 。
使用前五个或六个实际值的平均值作为 $S_0$ 。

下面我们生产一组没有趋势和季节性的白噪声时间序列，然后使用python的statsmodels包的SimpleExpSmoothing方法来拟合并预测未来10个值，这里我们设置不同的 $\alpha$ 值，来看看当设置不同的平滑参数时,拟合值的变化情况,这里需要说明的是简单指数平滑的方法只适用于没有趋势和季节性的时间序列数据，而白噪声是以0为均值呈现正太分布的序列，因此它正好适合用简单指数平滑的方法来预测。

np.random.seed(10)
y= np.random.normal(loc=0,scale=1,size=100)
df_noise = pd.DataFrame(y).rename(columns={0:'y'})

for alpha in [0.2 , 0.5, 0.8,1]:
    df_noise.plot.line()
    fit1 = SimpleExpSmoothing(df_noise).fit(smoothing_level = alpha  ,optimized=False)
    fcast1 = fit1.forecast(10).rename('alpha = ' + str(alpha))
    fcast1.plot(marker='o', legend=True,figsize=(12,4))
    fit1.fittedvalues.plot()
    plt.show()

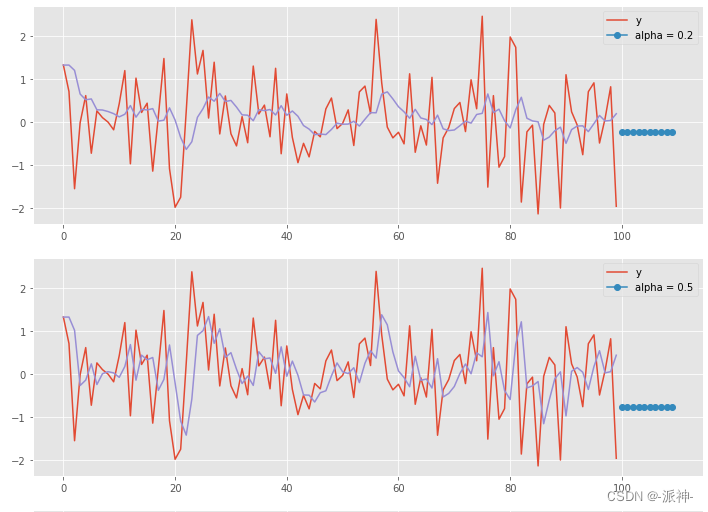
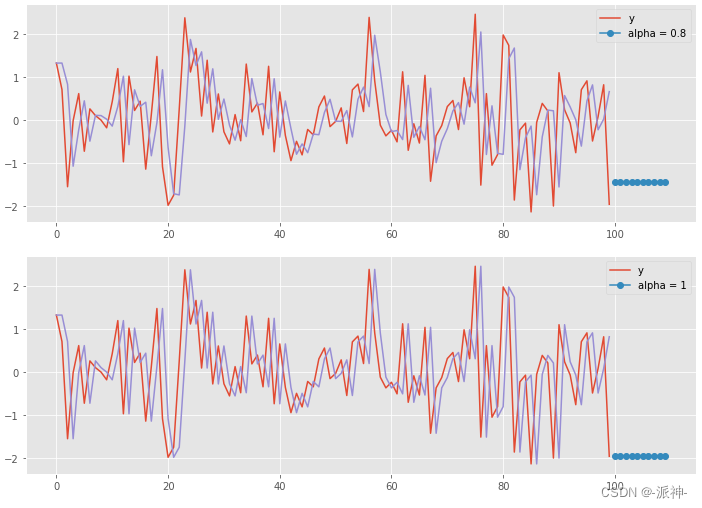
这里我们可以观察到当 $\alpha$ =0.2是，权重衰减的速度比较慢,也就是说更久远的过去值对未来值也会有较大的影响,所以拟合曲线总体比较平滑，当 $\alpha$ 逐渐变大时,权重衰减的速度加快，也就是说较近的过去值对未来值的影响变大了，更久远的过去值对未来的影响变小了，所以拟合曲线的形状更接近最近白噪声曲线,当 $\alpha$ =1时,拟合曲线的形状就像白噪声曲线向右平移了一个时刻,因为每一个时刻的拟合值正好等于之前一个时刻的白噪声的值。而我们未来的预测值(我们预测了10个预测值)都是相等的,当 $\alpha$ =1时预测值都等于最后一个白噪声值,这相当于我们的朴素预测法。

二.趋势法

Holt 趋势法

前面介绍的简单指数平滑预测法只适用于没有趋势和季节性的数据,因为它生成的预测值都是相等的即在水平方向生成所有的预测值,但是当原始数据存在趋势时，使用简单指数平滑预测法效果就会很差,因为它无法捕捉到数据的趋势,所以无法沿着数据的趋势方向来生成预测值。Holt (1957) 将简单指数平滑法扩展到可以预测具有趋势的数据。

下面我们来介绍一下基于趋势的指数平滑预测法的递归式(Holt)：

$S_t = \alpha X_t + (1 - \alpha) (S_{t-1} + b_{t-1})$

$b_t = \beta (S_t - S_{t-1}) + (1- \beta) b_{t-1}$

预测公式：

$\hat{X}_{t+h} = S_t + h b_t$

之前我们介绍的简单指数平滑法只有一个递归式，而趋势的指数平滑预测法有两个递归式 $S_t,b_t$ , 这里 $S_t$ 表示在 $t$ 时刻该时间序列的水平的估计值， $b_t$ 表示该时间序列在 $t$ 时刻的趋势（斜率）的估计， $\alpha$ 是水平的平滑参数( $0\le\alpha\le1$ ), $\beta$ 是趋势的平滑参数( $0\le\beta\le1$ )。

与简单的指数平滑一样，这里的水平方程表明 $S_t$ 是观测值在 t+1 时刻的预测值的加权平均值，这里由 $S_{t-1} + b_{t-1}$ 给出。趋势方程表明, $b_t$ 是基于 $S_t - S_{t-1}$ 和前一个趋势的估计值 $b_{t-1}$ 在 t 时刻的估计值的加权平均值。

这里的预测函数不再做水平方向预测，而是有趋势的。向前 h步预测值等于上一次估计的水平值加上前一个估计的趋势值的 h 倍。因此，预测值是一个关于 h的线性函数。

阻尼趋势方法(Damped trend methods)

Holt线性方法产生的预测值可以显示出未来的趋势，但会产生过度预测，尤其是对于更长远的预测而言。受此启发，Gardner & McKenzie (1985) 引入了一个参数，可以在未来某些时刻“平缓”趋势。

除了平滑参数 $\alpha$ 和 $\beta$ （在Holt方法中，取值介于0和1之间），该方法还包含一个阻尼参数 $0< \phi <1$

预测公式：

$\hat{X}_{t+h} = S_t + (\phi+\phi^2 + \dots + \phi^{h})b_{t}$

递归式：

$S_t = \alpha X_t + (1 - \alpha) (S_{t-1} + \phi b_{t-1})$

$b_t = \beta (S_t - S_{t-1}) + (1- \beta) \phi b_{t-1}$

如果 $\phi=1$ 则该方法与Holt趋势法相同。对于 0和 1之间的取值， $\phi$ 平缓了趋势，使其在将来某个时间接近一个常数。事实上，对于任意 $0<\phi<1$ 随着 $h\rightarrow\infty$ 预测值收敛到 $S_t+\phi b_t/(1-\phi)$ 。这意味着短期预测值有一定的趋势，而长期预测值则保持不变。 $\phi$ 的实际取值范围一般在 $0.8\le\phi\le0.98$ 。下面我们查看澳大利亚人口增长趋势图,该趋势图显示澳大利亚人口数量呈现近似线性增长趋势：

df=pd.read_csv('https://raw.githubusercontent.com/tongzm/ml-python/master/data/aus_economy.csv')[['Year','Population']]
df.set_index('Year').plot();

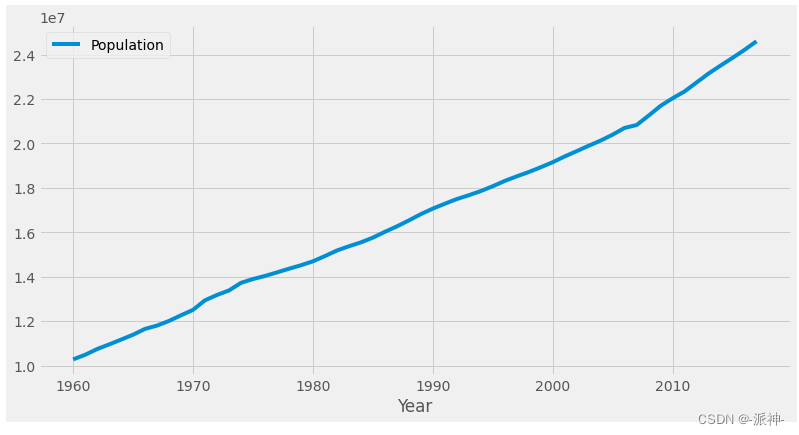
接下来我们使用简单指数平滑、趋势法、阻尼趋势法三种方法来预测澳大利亚未来10年的人口数量其中平滑参数 $\alpha,\beta$ ,阻尼参数 $\phi$ ,初始化参数 $S_0,b_0$ 我们都让算法来自动拟合出来,阻尼参数我们设置为0.9，下面我们我们调用statsmodels的SimpleExpSmoothing和Holt来实现简单指数平滑预测、趋势预测、阻尼趋势法预测：

from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt

fit1 = SimpleExpSmoothing(df.Population).fit()
fcast1 = fit1.forecast(10).rename(r'Simple ExpSmoothing')
fcast1.index=[i for i in range(df.Year.max()+1,df.Year.max()+11)]

fit2 = Holt(df.Population).fit()
fcast2 = fit2.forecast(10).rename("Holt's linear trend")
fcast2.index=[i for i in range(df.Year.max()+1,df.Year.max()+11)]

fit3 = Holt(df.Population, damped=True).fit(damping_slope=0.9)
fcast3 = fit3.forecast(10).rename("damped trend")
fcast3.index=[i for i in range(df.Year.max()+1,df.Year.max()+11)]

df1= df.set_index('Year')
df1=pd.concat([df1,fcast1,fcast2,fcast3],axis=1)
df1.plot();

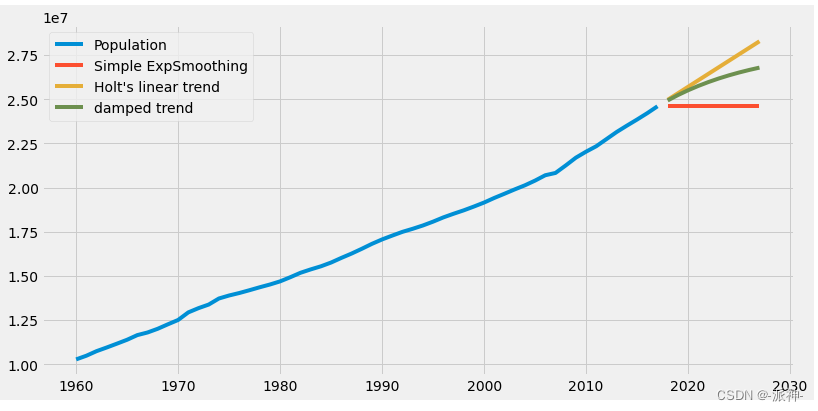
下面我们查看一下算法自动拟合出来的最佳参数：

params = ['smoothing_level', 'smoothing_trend', 'damping_trend', 'initial_level', 'initial_trend']
results=pd.DataFrame(index=[r"$\alpha$",r"$\beta$",r"$\phi$",r"$S_0$","$b_0$","SSE"] ,columns=['SimpleExpSmoothing', "Holt","Damped trend"])
results["SimpleExpSmoothing"] =[fit1.params[p] for p in params] + [fit1.sse]
results["Holt"] =[fit2.params[p] for p in params] + [fit2.sse]
results["Damped trend"] =[fit3.params[p] for p in params] + [fit3.sse]
results

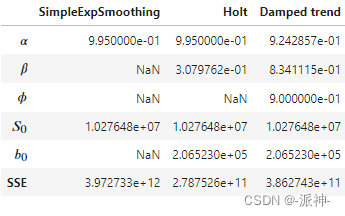
这里我们看到简单指数平滑法只存在 $\alpha,S_0$ 两个参数，Holt方法没有 $\phi$ 参数，而阻尼趋势法(Damped)包含了所有的参数，SSE指的是样本集内的误差平方和，最佳参数的组合会使得SSE最小。

三.Holt-Winters季节性方法

加法季节性

前面介绍的Holt趋势法有两个递归式，这里介绍的Holt-Winters季节性方法里有三个递归式定义如下：

$S_t = \alpha (X_t - c_{t - L}) + (1 - \alpha) (S_{t-1} + b_{t-1})$

$b_t = \beta (S_t - S_{t-1}) + (1- \beta) b_{t-1}$

$c_t = \gamma (X_t - S_{t-1} - b_{t-1})+ (1 - \gamma) c_{t-L}$

其中 $\alpha, \beta, \gamma \in (0,1)$

预测公式：

$\hat{X}_{t+h} = S_t + h b_t + c_{(t-L + h) \;\; mod \;\; L }$

这里 $S_t$ 表示在 $t$ 时刻该时间序列的水平的估计值， $b_t$ 表示该时间序列在 $t$ 时刻的趋势（斜率）的估计， $c_t$ 表示在 t 时刻的季节性估计值。 $L$ 表示季节性周期即一年内数据周期性变化的次数。如果数据是by day 的 $L$ 通常为7，如果数据是by month的 $L$ 通常为12，如果是数据by quarter的 $L$ 通常为4，但这不是绝对的，有时候需要通过计算自相关函数的极值数来确定 $L$ 。

下面我们使用statsmodels的ExponentialSmoothing来预测航空公司乘客数量，因为这个数据是月度数据，所以季节性周期是12，我们将使用加法季节性和乘法季节性(暂时没有介绍)两种方法来预测。我们会看到未来12个月预测值中乘法季节性的周期性变化的幅度比加法季节性的变化幅度要略大一点，这符合数据自身的特征，此外我们还要查看各个平滑参数的最优值，因为我们没有设置初始化的平滑参数(你也可以手动设置初始化平滑参数)，因此算法自动通过使用最小化SSE(误差平方和)的方法来拟合出最优的初始化平滑参数。

from statsmodels.tsa.holtwinters import ExponentialSmoothing
from sktime.datasets import load_airline
y = load_airline()

y.plot(figsize=(14,6),legend=True)
fit1 = ExponentialSmoothing(y, seasonal_periods=12, trend='add', seasonal='add')
fit1 = fit1.fit()
fit1.forecast(12).rename("seasonal additive").plot(color='b', legend=True)

fit2 = ExponentialSmoothing(y, seasonal_periods=12, trend='add', seasonal='mul')
fit2 = fit2.fit()
fit2.forecast(12).rename("seasonal multiplicative").plot(color='g', legend=True)

plt.show()

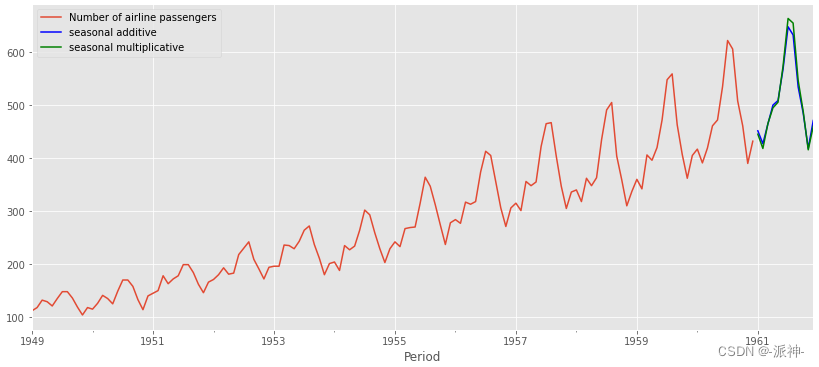
results=pd.DataFrame(index=[r"$\alpha$",r"$\beta$",r"$\phi$",r"$\gamma$",r"$S_0$","$b_0$","SSE"])
params = ['smoothing_level', 'smoothing_trend', 'damping_trend', 'smoothing_seasonal', 'initial_level', 'initial_trend']
results["Additive"]       = [fit1.params[p] for p in params] + [fit1.sse]
results["Multiplicative"] = [fit2.params[p] for p in params] + [fit2.sse]
results

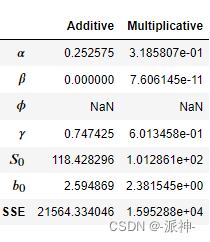
这里因为我们没有使用阻尼系数，因此 $\phi$ 参数为空。

四.指数平滑法的分类

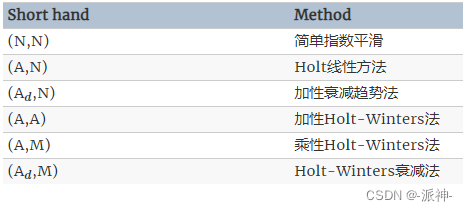
指数平滑法并不局限于前面介绍的这些方法。通过考虑趋势和季节性的不同组合变化，可以得到九种指数平滑方法，每种方法都由一对字母组合 (T,S) 标记，分别表示“趋势”和“季节”成分。例如， (A,M) 是具有加性趋势和乘性季节性的方法; (A $_d$ ,N) 是具有衰减趋势且没有季节性的方法等等。

其中一些方法我们已经知道它们有其他名称

在此基础上我们还可以推广出所有版本的指数平滑方法：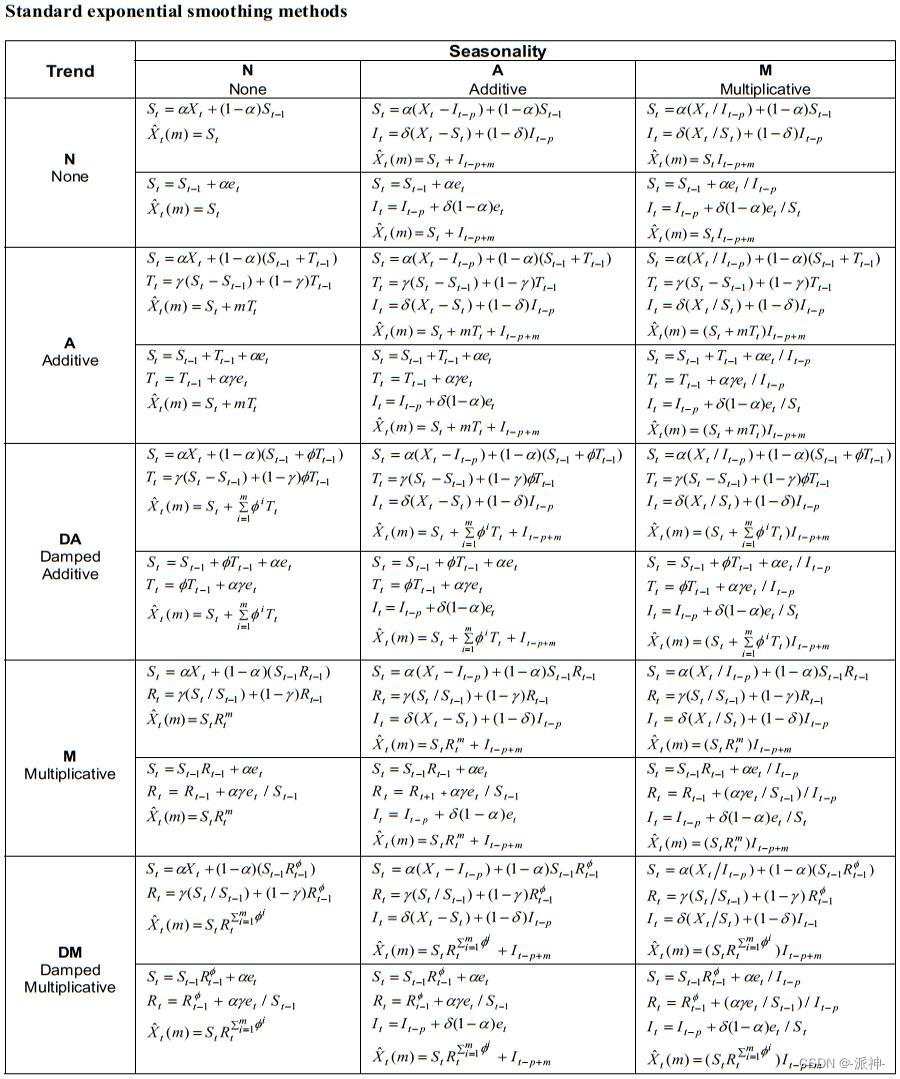

总结

今天我们主要介绍了指数平滑的一些基本方法如简单指数平滑,趋势法、阻尼趋势法，季节性法。需要说明的是本文主要参考了<<Forecasting: Principles and Practice>>并将书中原来用R语言实现的算法用Python实现了一下，在python代码中调用的指数平滑算法包主要来自于statsmodels包。通过对<<Forecasting: Principles and Practice>>的学习并结合对statsmodels包的练习可以更加深刻的解指数平滑的原理。

参考质料

Forecasting: Principles and Practice (3rd ed)

Exponential smoothing — statsmodels

标签：时间序列时间序列预测数据分析

本文转载自: https://blog.csdn.net/weixin_42608414/article/details/126540698
版权归原作者 -派神- 所有，如有侵权，请联系我们删除。

时间序列的数据分析(六):指数平滑预测法

一.简单指数平滑预测(Brown)

二.趋势法

Holt 趋势法

阻尼趋势方法(Damped trend methods)

三.Holt-Winters季节性方法

加法季节性

四.指数平滑法的分类

总结

参考质料

发表评论

“时间序列的数据分析(六):指数平滑预测法”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航