本文深入探讨生成式AI的核心技术,包括GANs、VAEs、自回归模型和Transformers,详细描述其原理、实现方法及实际应用,结合代码示例和现实案例,展示最新技术进展和应用场景。
关注作者,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人
目录

一、引言
生成式AI(Generative AI)作为人工智能的一个重要分支,通过学习大量的数据生成新的数据样本,在多个领域取得了令人瞩目的进展。生成式AI不仅在学术研究中激发了广泛的兴趣,也在工业应用中展示了巨大的潜力,推动了图像生成、文本生成、视频生成等领域的快速发展。
生成对抗网络(GANs)的突破
生成对抗网络(Generative Adversarial Networks, GANs)由Ian Goodfellow等人在2014年提出,通过生成器和判别器之间的博弈学习,GANs在图像生成领域取得了显著的成功。例如,StyleGAN3能够生成极其逼真的高分辨率人脸图像,在图像生成质量和细节处理方面达到了新的高度。
变分自编码器(VAEs)和自回归模型的进展
变分自编码器(Variational Autoencoders, VAEs)和自回归模型在生成数据时通过对输入数据进行概率建模,提供了生成数据的新方式。VAEs在生成逼真的数据分布方面表现出色,而自回归模型如GPT-3在文本生成任务中展示了强大的能力。
变换模型(Transformers)的应用
变换模型(Transformers)通过其强大的并行处理能力和自注意力机制,在自然语言处理和多模态生成任务中取得了突破性进展。GPT-3和最新的GPT-4模型展示了前所未有的语言理解和生成能力,广泛应用于文本生成、翻译、对话系统等领域。
实际应用的广泛拓展
生成式AI在实际应用中的潜力逐渐显现。图像生成技术被广泛应用于艺术创作、广告设计和电影特效中;文本生成技术在自动化写作、聊天机器人和语言翻译中取得了显著进展;在医疗和科学研究中,生成式AI帮助预测蛋白质结构、设计新药物和分析医学影像,为科学发现提供了新的工具。
技术挑战与未来发展
尽管生成式AI在多个领域取得了显著进展,但仍面临诸多挑战,如模型训练的不稳定性、数据隐私和伦理问题、生成内容的真实性和安全性等。未来,随着技术的不断创新和优化,生成式AI有望在更广泛的领域中发挥更大的作用,推动科学技术和社会进步。
二、生成对抗网络GANs
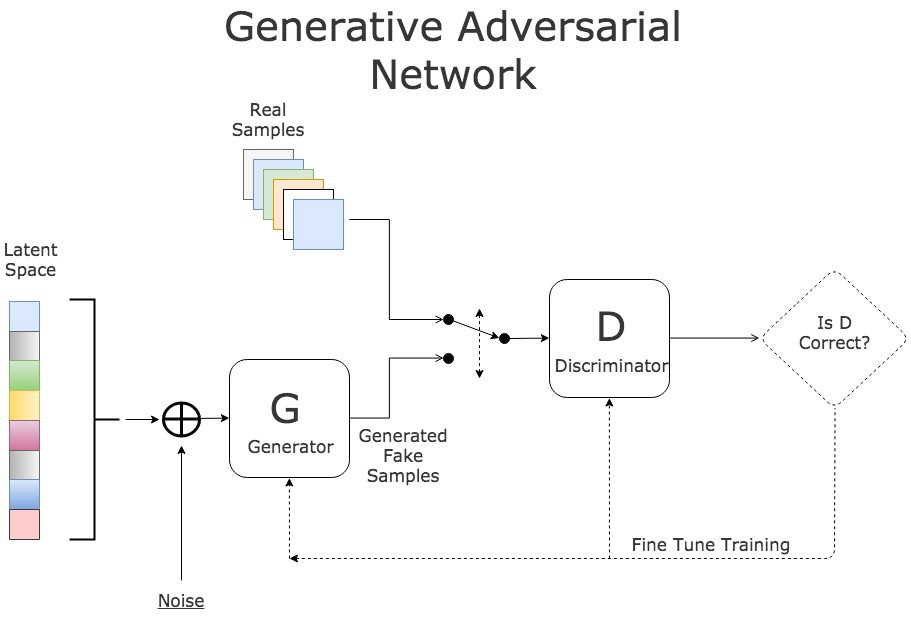
生成对抗网络(Generative Adversarial Networks, GANs)是生成式AI领域的一个重要突破。自2014年由Ian Goodfellow等人提出以来,GANs迅速成为生成模型的一个主要方向,通过其独特的对抗训练机制,GANs在图像生成、数据增强和许多其他应用中表现出了卓越的能力。
GANs的基本概念
GANs由两个主要部分组成:生成器(Generator)和判别器(Discriminator)。生成器负责从随机噪声中生成数据,试图欺骗判别器;而判别器则尝试区分真实数据和生成数据。两者通过对抗性训练不断优化,最终生成器能够生成逼真的数据。
生成器(Generator)
生成器的任务是接收随机噪声向量,并将其转换为类似于训练数据的样本。其架构通常采用反卷积神经网络(Transposed Convolutional Neural Networks)来实现数据的上采样。
import torch
import torch.nn as nn
classGenerator(nn.Module):def__init__(self):super(Generator, self).__init__()
self.main = nn.Sequential(
nn.ConvTranspose2d(100,512,4,1,0, bias=False),
nn.BatchNorm2d(512),
nn.ReLU(True),
nn.ConvTranspose2d(512,256,4,2,1, bias=False),
nn.BatchNorm2d(256),
nn.ReLU(True),
nn.ConvTranspose2d(256,128,4,2,1, bias=False),
nn.BatchNorm2d(128),
nn.ReLU(True),
nn.ConvTranspose2d(128,64,4,2,1, bias=False),
nn.BatchNorm2d(64),
nn.ReLU(True),
nn.ConvTranspose2d(64,3,4,2,1, bias=False),
nn.Tanh())defforward(self,input):return self.main(input)# 初始化生成器并显示结构
netG = Generator()print(netG)
判别器(Discriminator)
判别器的任务是接收数据样本,并判断其是否为真实数据。其架构通常采用卷积神经网络(Convolutional Neural Networks)来实现数据的下采样。
classDiscriminator(nn.Module):def__init__(self):super(Discriminator, self).__init__()
self.main = nn.Sequential(
nn.Conv2d(3,64,4,2,1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64,128,4,2,1, bias=False),
nn.BatchNorm2d(128),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(128,256,4,2,1, bias=False),
nn.BatchNorm2d(256),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(256,512,4,2,1, bias=False),
nn.BatchNorm2d(512),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(512,1,4,1,0, bias=False),
nn.Sigmoid())defforward(self,input):return self.main(input)# 初始化判别器并显示结构
netD = Discriminator()print(netD)
GANs的训练机制
GANs的训练过程可以看作一个博弈过程,生成器和判别器通过交替优化,最终达到一个纳什均衡。在训练过程中,生成器的目标是最大化判别器判断错误的概率,而判别器的目标是最大化正确判断的概率。具体而言,训练目标可以通过以下公式表示:
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]
GminDmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
训练过程的代码示例
以下是使用PyTorch进行GANs训练的基本代码框架:
import torch.optim as optim
# 损失函数和优化器
criterion = nn.BCELoss()
optimizerD = optim.Adam(netD.parameters(), lr=0.0002, betas=(0.5,0.999))
optimizerG = optim.Adam(netG.parameters(), lr=0.0002, betas=(0.5,0.999))for epoch inrange(num_epochs):for i, data inenumerate(dataloader,0):# 更新判别器
netD.zero_grad()
real = data[0].to(device)
batch_size = real.size(0)
label = torch.full((batch_size,), real_label, device=device)
output = netD(real).view(-1)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()
noise = torch.randn(batch_size,100,1,1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach()).view(-1)
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()# 更新生成器
netG.zero_grad()
label.fill_(real_label)
output = netD(fake).view(-1)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()# 打印训练进度if i %50==0:print(f'[{epoch}/{num_epochs}][{i}/{len(dataloader)}] 'f'Loss_D: {errD.item():.4f} Loss_G: {errG.item():.4f} 'f'D(x): {D_x:.4f} D(G(z)): {D_G_z1:.4f} / {D_G_z2:.4f}')
实际应用案例
图像生成
GANs在图像生成领域取得了显著的成果。StyleGAN3是由NVIDIA提出的一种高级GAN模型,能够生成高分辨率的逼真人脸图像。其主要创新在于改进了生成器的架构和训练过程,使得生成的图像在细节和整体结构上更加逼真。
数据增强
在数据科学和机器学习中,数据不足是一个常见的问题。GANs可以通过生成新的数据样本来增强训练数据集,尤其在医学图像、文本数据等领域应用广泛。例如,在医学图像处理中,GANs可以生成新的病变样本,从而提高疾病检测模型的性能。
艺术创作
GANs在艺术创作中的应用也非常广泛。通过训练GANs模型生成艺术作品,艺术家和设计师能够探索新的创作风格和表达方式。例如,DeepArt使用GANs技术生成艺术风格的图像,为用户提供个性化的艺术创作服务。
三、变分自编码器VAEs
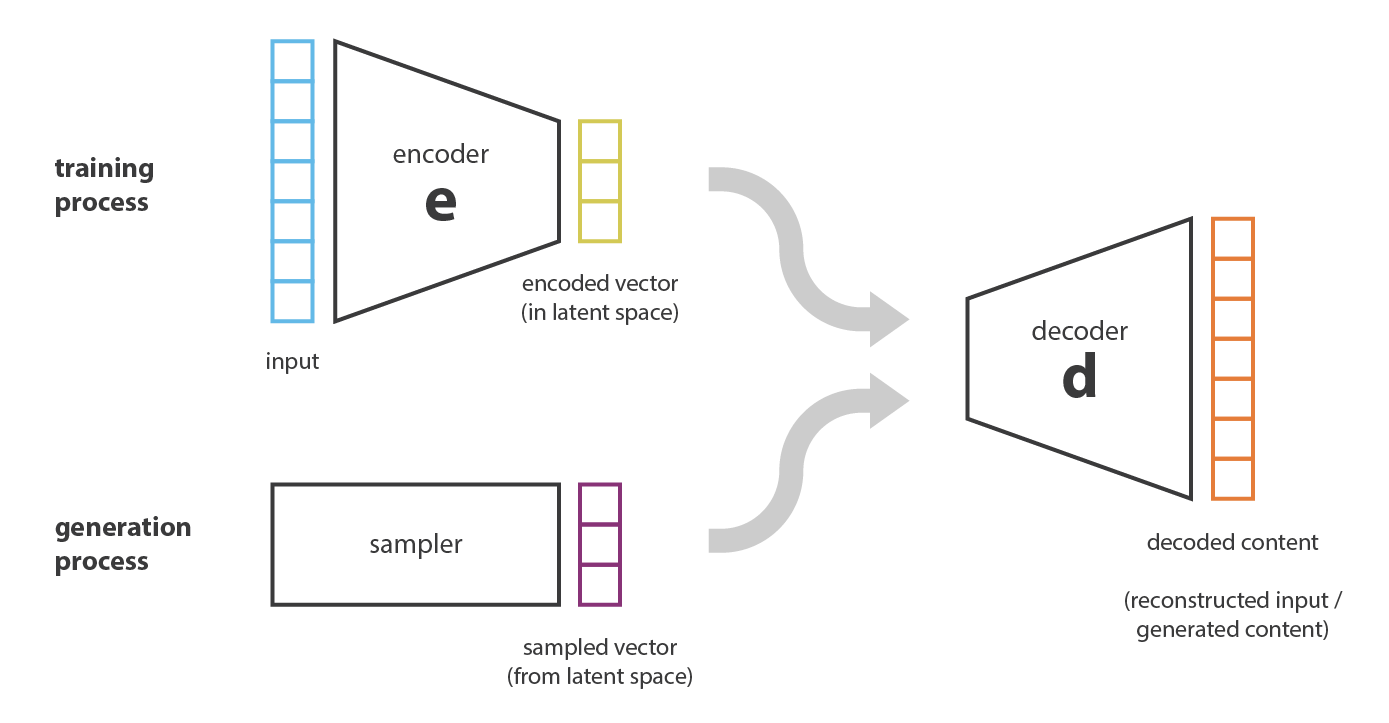
变分自编码器(Variational Autoencoders, VAEs)是生成式AI的另一核心技术。VAEs通过引入概率模型和变分推断,解决了传统自编码器在生成新数据时的局限性。VAEs在图像生成、数据降维和异常检测等方面具有重要应用。
VAEs的基本概念
自编码器的局限性
传统自编码器(Autoencoders)通过编码器(Encoder)将输入数据压缩成潜在表示,再通过解码器(Decoder)重建输入数据。然而,传统自编码器在生成新数据时存在局限,因为其潜在空间并未显式建模概率分布。
变分自编码器的原理
变分自编码器(VAEs)通过引入概率建模,解决了传统自编码器的生成问题。其核心思想是将输入数据映射到一个已知分布(通常是高斯分布)的潜在空间,并通过最大化证据下界(ELBO)进行优化。
变分自编码器的目标是通过以下步骤实现:
- 编码器:将输入数据( x )映射到潜在表示( z )的条件概率分布 ( q(z|x) )。
- 解码器:从潜在表示 ( z ) 生成数据 ( x ) 的条件概率分布 ( p(x|z) )。
- 优化目标:最大化变分下界(ELBO),其公式为: L ( x ; θ , ϕ ) = E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) \mathcal{L}(x; \theta, \phi) = \mathbb{E}{q_\phi(z|x)}[\log p_\theta(x|z)] - D{KL}(q_\phi(z|x) || p(z)) L(x;θ,ϕ)=Eqϕ(z∣x)[logpθ(x∣z)]−DKL(qϕ(z∣x)∣∣p(z)) 其中,( D_{KL} ) 表示Kullback-Leibler散度,用于衡量两种分布之间的差异。
编码器和解码器的实现
以下是一个使用PyTorch实现VAEs的基本代码示例:
import torch
import torch.nn as nn
import torch.nn.functional as F
classVAE(nn.Module):def__init__(self, input_dim, hidden_dim, latent_dim):super(VAE, self).__init__()# 编码器
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2_mean = nn.Linear(hidden_dim, latent_dim)
self.fc2_logvar = nn.Linear(hidden_dim, latent_dim)# 解码器
self.fc3 = nn.Linear(latent_dim, hidden_dim)
self.fc4 = nn.Linear(hidden_dim, input_dim)defencode(self, x):
h1 = F.relu(self.fc1(x))return self.fc2_mean(h1), self.fc2_logvar(h1)defreparameterize(self, mu, logvar):
std = torch.exp(0.5* logvar)
eps = torch.randn_like(std)return mu + eps * std
defdecode(self, z):
h3 = F.relu(self.fc3(z))return torch.sigmoid(self.fc4(h3))defforward(self, x):
mu, logvar = self.encode(x)
z = self.reparameterize(mu, logvar)return self.decode(z), mu, logvar
# 初始化VAE并显示结构
input_dim =784# 以MNIST数据集为例
hidden_dim =400
latent_dim =20
vae = VAE(input_dim, hidden_dim, latent_dim)print(vae)
损失函数的实现
在训练VAEs时,需要定义合适的损失函数,包括重构损失和KL散度损失。以下是实现代码:
defloss_function(recon_x, x, mu, logvar):
BCE = F.binary_cross_entropy(recon_x, x, reduction='sum')
KLD =-0.5* torch.sum(1+ logvar - mu.pow(2)- logvar.exp())return BCE + KLD
VAEs的实际应用
图像生成
VAEs在图像生成中的应用广泛,例如在MNIST数据集上,VAEs能够生成逼真的手写数字图像。通过对潜在空间的采样,可以生成无限多样的图像样本,提升图像生成任务的多样性。
数据降维
VAEs通过对数据进行压缩和重构,能够有效地进行数据降维和特征提取。与PCA等传统降维方法相比,VAEs能够捕捉数据的非线性结构,提供更为丰富的潜在表示。
异常检测
由于VAEs在重构正常数据时表现优异,且在处理异常数据时重构误差较大,因此VAEs被广泛应用于异常检测。例如,在工业设备故障检测中,VAEs可以通过监测重构误差,及时发现设备异常情况。
四、自回归模型Autoregressive Models
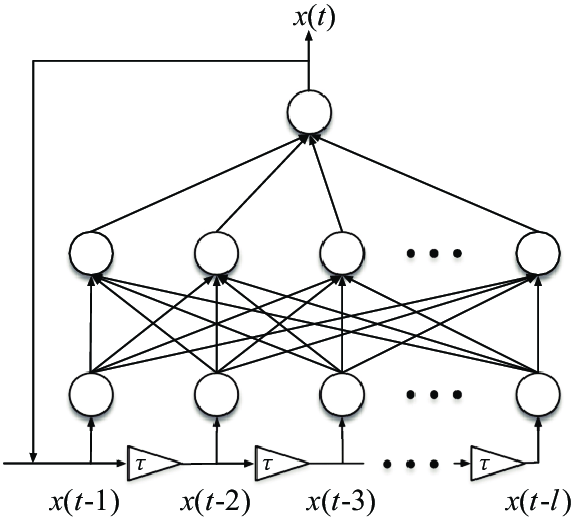
自回归模型(Autoregressive Models)是生成式AI中的一个重要类别,通过建模数据序列中的条件依赖关系,自回归模型能够逐步生成序列数据,如文本、音频和图像。自回归模型在自然语言处理、语音生成和图像生成等领域有着广泛的应用。
自回归模型的基本概念
自回归模型的定义
自回归模型是一种统计模型,用于描述数据序列中的依赖关系。其基本思想是当前时刻的数据依赖于之前时刻的数据。在生成式AI中,自回归模型通过逐步预测下一个数据点,从而生成整个序列。
自回归模型的公式表示
自回归模型的生成过程可以表示为:
p
(
x
1
,
x
2
,
…
,
x
T
)
=
∏
t
=
1
T
p
(
x
t
∣
x
t
−
1
,
…
,
x
1
)
p(x_1, x_2, \ldots, x_T) = \prod_{t=1}^T p(x_t | x_{t-1}, \ldots, x_1)
p(x1,x2,…,xT)=t=1∏Tp(xt∣xt−1,…,x1)
其中,( x_t ) 表示序列中第 ( t ) 个数据点,( p(x_t | x_{t-1}, \ldots, x_1) ) 表示在已知前 ( t-1 ) 个数据点的情况下,生成第 ( t ) 个数据点的条件概率。
自回归模型的实现
基本的自回归模型
最简单的自回归模型是线性自回归模型(Autoregressive Integrated Moving Average, ARIMA),其假设当前时刻的数据是之前数据的线性组合。对于生成式AI,我们通常使用更复杂的深度学习模型,如循环神经网络(RNNs)、长短期记忆网络(LSTMs)和变换模型(Transformers)。
使用RNN实现自回归模型
以下是使用PyTorch实现简单RNN的代码示例,用于生成文本序列:
import torch
import torch.nn as nn
import torch.optim as optim
# 定义RNN模型classRNNModel(nn.Module):def__init__(self, input_size, hidden_size, output_size):super(RNNModel, self).__init__()
self.hidden_size = hidden_size
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)defforward(self, x, hidden):
out, hidden = self.rnn(x, hidden)
out = self.fc(out)return out, hidden
definit_hidden(self, batch_size):return torch.zeros(1, batch_size, self.hidden_size)# 参数设置
input_size =10
hidden_size =20
output_size =10
batch_size =5
seq_length =15# 初始化模型和参数
model = RNNModel(input_size, hidden_size, output_size)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)# 生成数据示例
data = torch.randn(batch_size, seq_length, input_size)
labels = torch.randint(0, output_size,(batch_size, seq_length))# 训练模型
hidden = model.init_hidden(batch_size)
model.train()for epoch inrange(10):
optimizer.zero_grad()
output, hidden = model(data, hidden)
loss = criterion(output.view(-1, output_size), labels.view(-1))
loss.backward()
optimizer.step()print(f'Epoch {epoch+1}, Loss: {loss.item()}')
自回归模型的应用
自然语言处理
自回归模型在自然语言处理(NLP)中的应用最为广泛,如GPT-3等预训练语言模型。GPT-3是一种大规模自回归语言模型,能够生成高质量的自然语言文本。其基本思想是基于给定的上下文逐字生成文本,使生成的内容连贯且符合语法规则。
语音生成
在语音生成领域,自回归模型也表现出了强大的能力。例如,WaveNet是一种基于自回归模型的语音生成网络,通过建模音频样本的条件概率,能够生成高质量的语音信号。WaveNet的生成过程逐样本进行,使得生成的语音自然且细腻。
图像生成
自回归模型在图像生成中的应用包括PixelRNN和PixelCNN,这些模型通过逐像素生成图像,能够捕捉图像中的复杂依赖关系。例如,PixelCNN通过建模每个像素的条件概率分布,生成高质量的图像。
五、Transformers
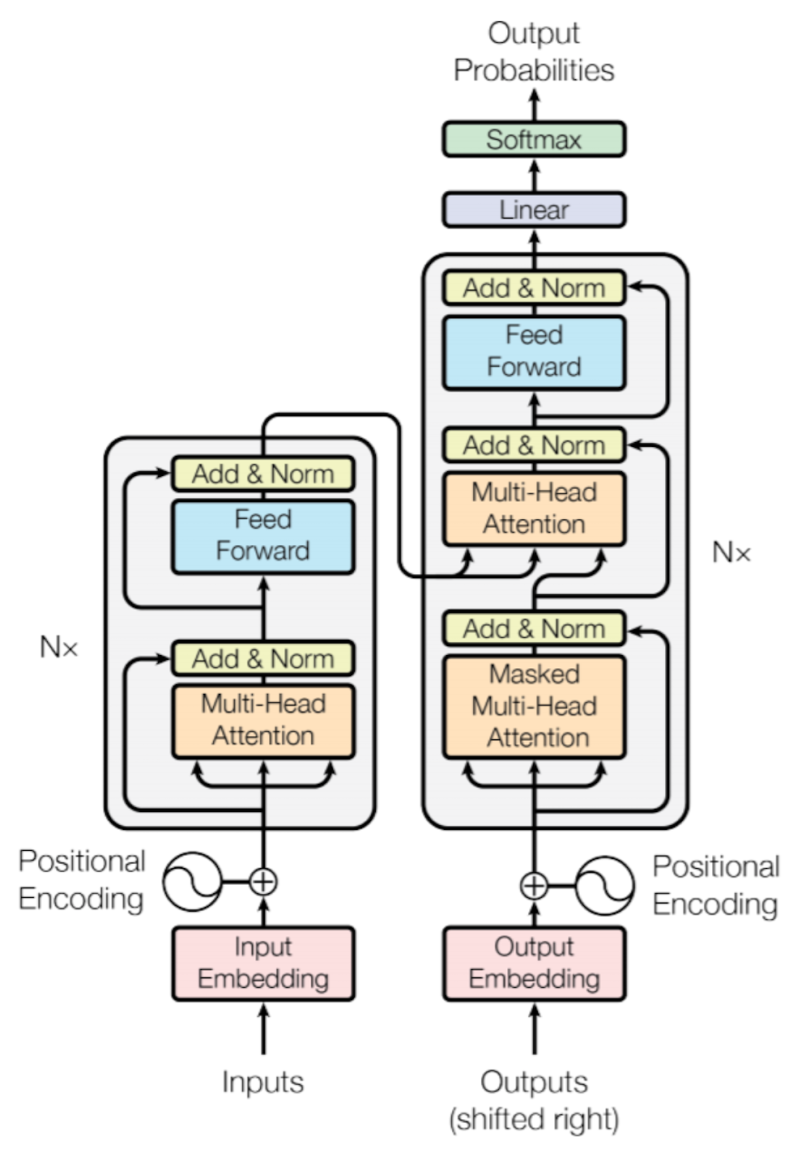
变换模型(Transformers)在近年来成为生成式AI领域的一个革命性技术。自从Vaswani等人在2017年提出以来,Transformers在自然语言处理(NLP)、计算机视觉(CV)和跨模态生成任务中展示了卓越的性能和广泛的应用。Transformers的核心优势在于其强大的并行计算能力和高效处理长距离依赖关系的能力。
Transformers的基本概念
注意力机制
Transformers的核心在于其注意力机制,尤其是自注意力机制(Self-Attention)。注意力机制允许模型在处理每个输入时关注整个输入序列,从而捕捉到全局依赖关系。具体来说,自注意力机制计算输入序列中每个元素与其他元素之间的相关性,然后基于这些相关性进行加权求和,从而生成新的表示。
多头注意力
多头注意力(Multi-Head Attention)通过并行多个注意力机制,进一步增强了模型捕捉不同特征和依赖关系的能力。多头注意力的公式表示如下:
MultiHead
(
Q
,
K
,
V
)
=
Concat
(
head
1
,
head
2
,
…
,
head
h
)
W
O
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_h)W^O
MultiHead(Q,K,V)=Concat(head1,head2,…,headh)WO
其中, ( \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) ),( Q )、( K )、( V ) 分别表示查询、键和值。
位置编码
由于Transformers不具有递归结构,需要引入位置编码(Positional Encoding)来注入序列中元素的位置信息。位置编码通常采用正弦和余弦函数定义:
P
E
(
p
o
s
,
2
i
)
=
sin
(
p
o
s
/
1000
0
2
i
/
d
m
o
d
e
l
)
PE_{(pos, 2i)} = \sin(pos / 10000^{2i/d_{model}})
PE(pos,2i)=sin(pos/100002i/dmodel)
P
E
(
p
o
s
,
2
i
+
1
)
=
cos
(
p
o
s
/
1000
0
2
i
/
d
m
o
d
e
l
)
PE_{(pos, 2i+1)} = \cos(pos / 10000^{2i/d_{model}})
PE(pos,2i+1)=cos(pos/100002i/dmodel)
编码器-解码器架构
Transformers采用编码器-解码器架构。编码器由多个编码层组成,每个编码层包含多头注意力和前馈神经网络(Feed-Forward Neural Network, FFN);解码器也由多个解码层组成,除了类似编码器的多头注意力和FFN外,还包含用于处理编码器输出的交叉注意力(Cross-Attention)。
以下是一个基于PyTorch实现的简化Transformer编码器的代码示例:
import torch
import torch.nn as nn
classMultiHeadAttention(nn.Module):def__init__(self, embed_size, heads):super(MultiHeadAttention, self).__init__()
self.embed_size = embed_size
self.heads = heads
self.head_dim = embed_size // heads
assert self.head_dim * heads == embed_size,"Embedding size needs to be divisible by heads"
self.values = nn.Linear(self.head_dim, embed_size, bias=False)
self.keys = nn.Linear(self.head_dim, embed_size, bias=False)
self.queries = nn.Linear(self.head_dim, embed_size, bias=False)
self.fc_out = nn.Linear(embed_size, embed_size)defforward(self, values, keys, query, mask):
N = query.shape[0]
value_len, key_len, query_len = values.shape[1], keys.shape[1], query.shape[1]
values = values.reshape(N, value_len, self.heads, self.head_dim)
keys = keys.reshape(N, key_len, self.heads, self.head_dim)
queries = query.reshape(N, query_len, self.heads, self.head_dim)
energy = torch.einsum("nqhd,nkhd->nhqk",[queries, keys])if mask isnotNone:
energy = energy.masked_fill(mask ==0,float("-1e20"))
attention = torch.softmax(energy /(self.embed_size **(1/2)), dim=3)
out = torch.einsum("nhql,nlhd->nqhd",[attention, values]).reshape(
N, query_len, self.embed_size
)
out = self.fc_out(out)return out
classTransformerBlock(nn.Module):def__init__(self, embed_size, heads, dropout, forward_expansion):super(TransformerBlock, self).__init__()
self.attention = MultiHeadAttention(embed_size, heads)
self.norm1 = nn.LayerNorm(embed_size)
self.norm2 = nn.LayerNorm(embed_size)
self.feed_forward = nn.Sequential(
nn.Linear(embed_size, forward_expansion * embed_size),
nn.ReLU(),
nn.Linear(forward_expansion * embed_size, embed_size))
self.dropout = nn.Dropout(dropout)defforward(self, value, key, query, mask):
attention = self.attention(value, key, query, mask)
x = self.dropout(self.norm1(attention + query))
forward = self.feed_forward(x)
out = self.dropout(self.norm2(forward + x))return out
classEncoder(nn.Module):def__init__(self, embed_size, num_layers, heads, device, forward_expansion, dropout, max_length):super(Encoder, self).__init__()
self.embed_size = embed_size
self.device = device
self.word_embedding = nn.Embedding(max_length, embed_size)
self.position_embedding = nn.Embedding(max_length, embed_size)
self.layers = nn.ModuleList([
TransformerBlock(
embed_size,
heads,
dropout=dropout,
forward_expansion=forward_expansion,)for _ inrange(num_layers)])
self.dropout = nn.Dropout(dropout)defforward(self, x, mask):
N, seq_length = x.shape
positions = torch.arange(0, seq_length).expand(N, seq_length).to(self.device)
out = self.dropout(self.word_embedding(x)+ self.position_embedding(positions))for layer in self.layers:
out = layer(out, out, out, mask)return out
# 初始化编码器并显示结构
embed_size =512
num_layers =6
heads =8
device = torch.device("cuda"if torch.cuda.is_available()else"cpu")
forward_expansion =4
dropout =0.1
max_length =100
encoder = Encoder(embed_size, num_layers, heads, device, forward_expansion, dropout, max_length).to(device)print(encoder)
Transformers的应用
自然语言处理
在自然语言处理(NLP)领域,Transformers表现出了强大的能力。基于Transformers的BERT(Bidirectional Encoder Representations from Transformers)和GPT(Generative Pre-trained Transformer)模型,显著提升了机器翻译、文本生成、问答系统等任务的性能。例如,OpenAI的GPT-3模型能够生成高质量的自然语言文本,广泛应用于对话系统、内容创作和代码生成等领域 。
计算机视觉
Transformers在计算机视觉领域也取得了重要进展。ViT(Vision Transformer)通过将图像划分为固定大小的块,并将每个块视为一个序列元素,利用Transformers的注意力机制处理图像数据。ViT在图像分类任务中取得了优异的性能,与传统的卷积神经网络(CNN)相比,展示了Transformers在视觉任务中的潜力 。
跨模态生成
Transformers在跨模态生成任务中表现出色,如OpenAI的DALL-E模型。DALL-E通过将文本描述转换为图像,展示了Transformers在处理多模态数据方面的强大能力。该模型能够生成高质量的图像,广泛应用于艺术创作、广告设计和内容生成等领域 。
版权归原作者 TechLead KrisChang 所有, 如有侵权,请联系我们删除。