前言
活动地址:CSDN21天学习挑战赛
🌍 python很适合机器学习领域,给大家推荐一款好用的刷题网站:《牛客网》
🌍 用来做一些练习快速熟悉基本语法非常的棒,而且题解也是非常的丰富
🚀 个人主页:阿阿阿阿锋的主页_CSDN
🌊 本文整理了从模型,到损失,再到损失关于权值的梯度的一些思路
🔥 希望和大家一起加油,一起进步!

文章目录
1. 模型
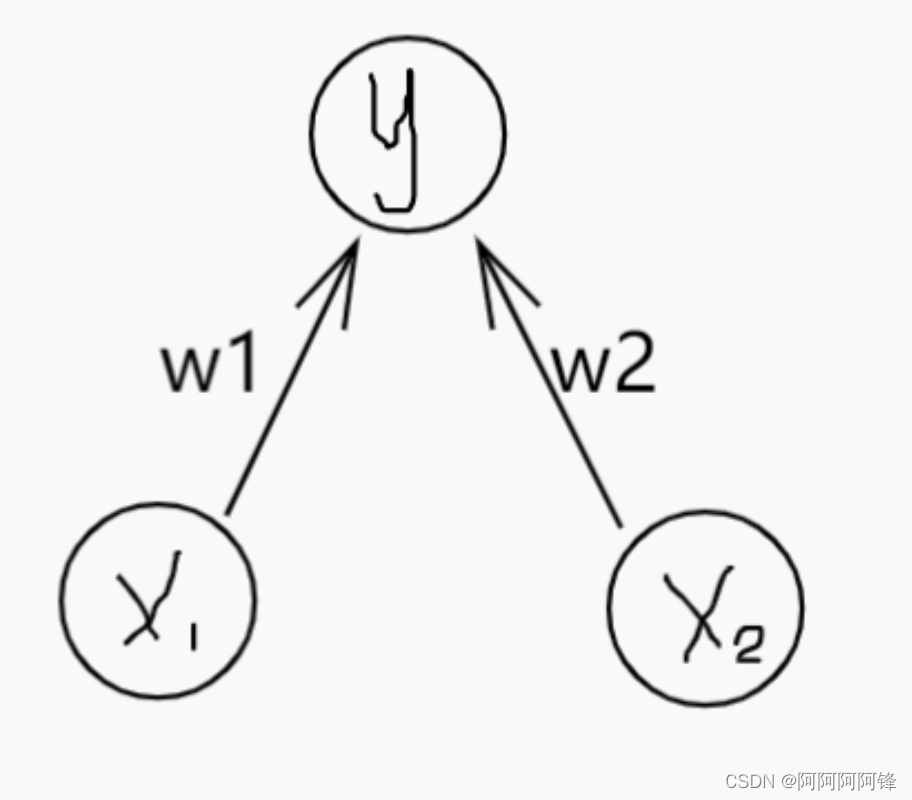
神经网络的模型可以就看作为一个函数,模型学习(训练)的过程,就可以看成是给函数寻找合适的参数的过程。比如,下面就是一个简单的模型,它所表示的函数就是
y
=
w
1
x
1
+
w
2
x
2
y = w1x1+w2x2
y=w1x1+w2x2
这个函数在两个侧面的投影,就是
y
=
w
1
x
1
y=w1x1
y=w1x1 和
y
=
w
2
x
2
y=w2x2
y=w2x2。学习一个多元函数,可以看成是分别学习多个一元的函数。

2. 损失
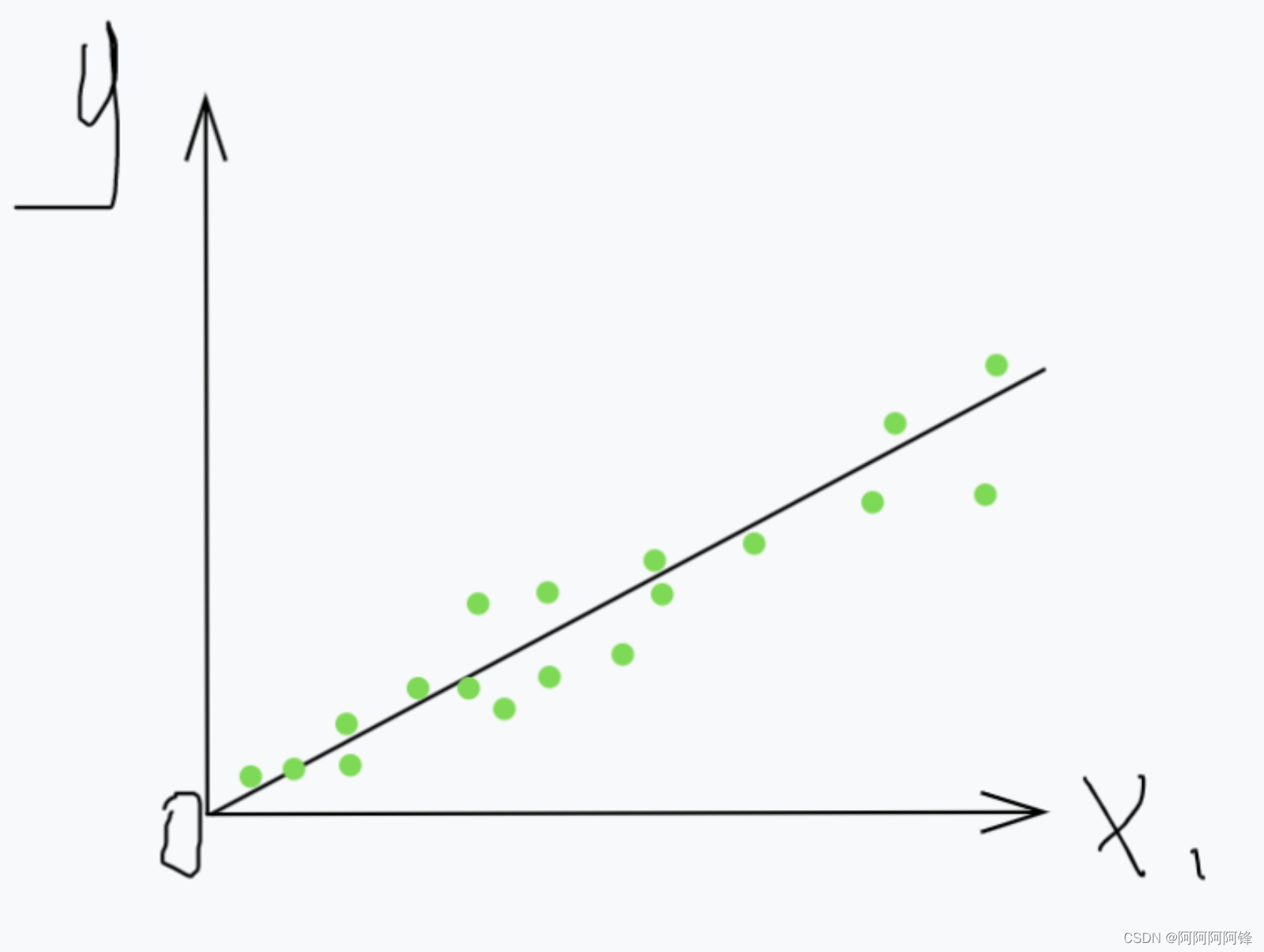
损失,也就是模型和数据的不贴合程度。
衡量损失常用的一个函数是均方损失函数:
l
o
s
s
=
∑
i
=
1
n
(
y
i
^
−
y
i
)
2
loss=\displaystyle\sum_{i=1}^n(\hat{y_{i}}-y_{i})^2
loss=i=1∑n(yi^−yi)2,其中 n 为数据点数量。
函数也可以写成
l
o
s
s
=
∑
i
=
1
n
(
W
X
i
−
y
i
)
2
loss=\displaystyle\sum_{i=1}^n(WX_{i}-y_{i})^2
loss=i=1∑n(WXi−yi)2,其中 W 为模型的所有权值,
X
i
X_{i}
Xi 为第 i 个数据点的所有自变量。
既然衡量损失有了一个确定的函数,那训练模型的过程就可以变成一个最小化损失的过程,方法就是不断地改变权值W,使函数关于所有这些数据点的损失(或者说平均损失)不断变小。
3. 损失loss关于权值W的梯度
通常来说,应该函数的权值 W 是固定的,而数据的特征 X 作为自变量。但我们是要通过一个固有的数据集,来优化权值W,所以在优化过程中,我们要把损失函数
l
o
s
s
loss
loss中的**W看作自变量**。
然后我们求
l
o
s
s
loss
loss 关于
W
W
W 的梯度,遵循着梯度的指引来改变
W
W
W。
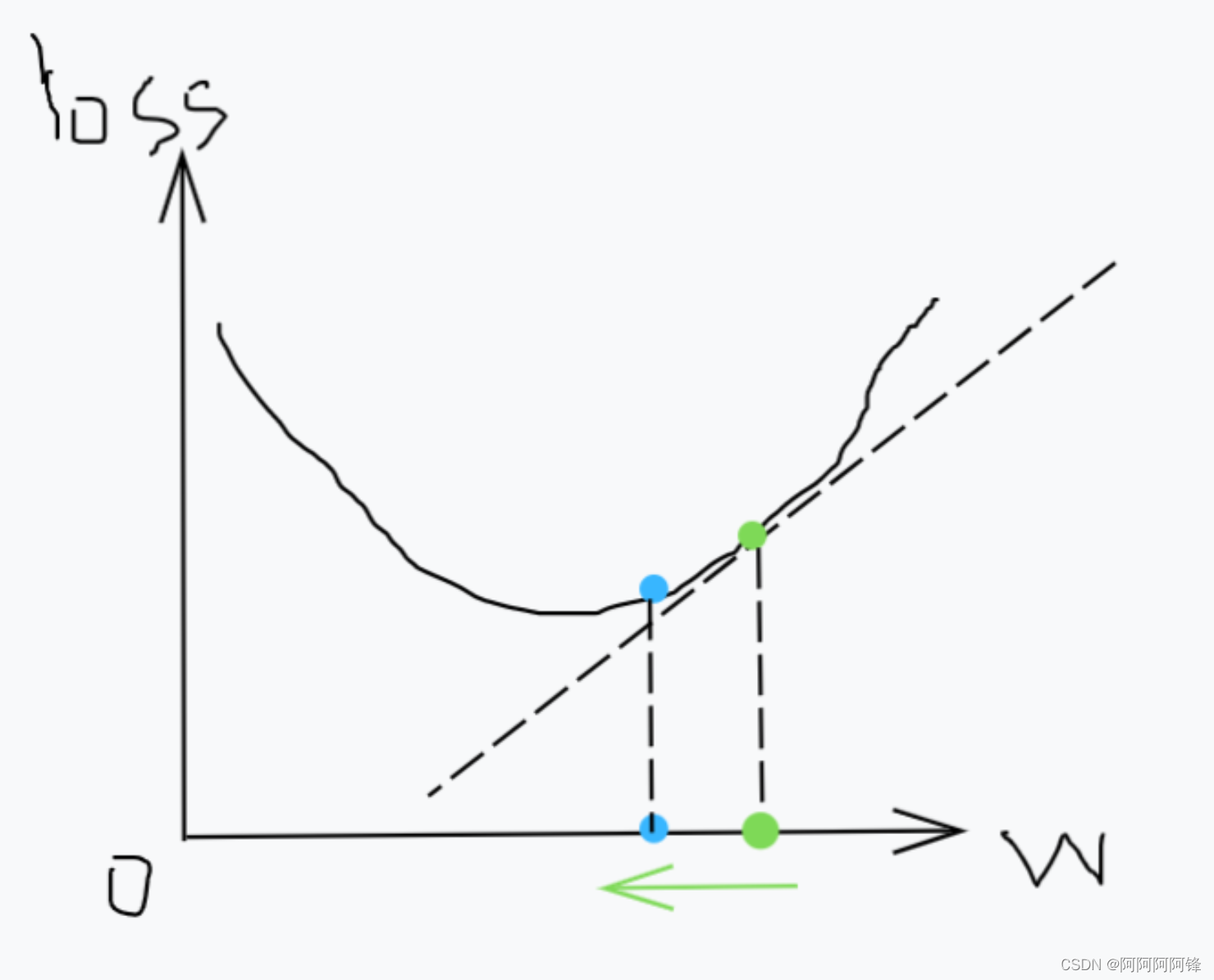
如果某个权值的梯度是正的,说明随着权值
w w w的增大,损失 l o s s loss loss也会增大。那我们为了让损失变小,就要减小 w w w的值。同样,如果梯度是负的,我们就要增大对应的权值。
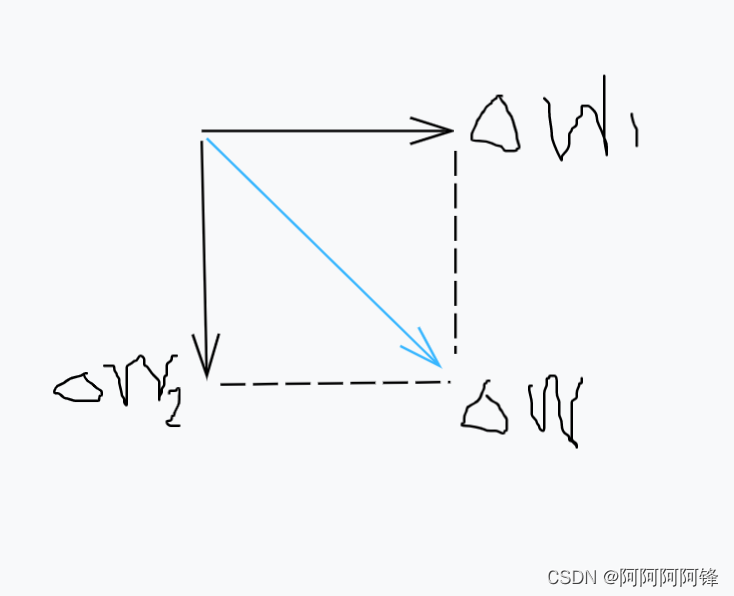
W
W
W 中的每个
w
w
w 的移动,可以看成是相对独立、互不干扰的。更新一个有很多权值的复杂模型,就成了很多重复的这样更新单个权值的操作。
4. 求梯度——数值梯度
在具体求梯度的过程中,计算机本身是不会公式演算的。但我们并不需要对损失函数求出梯度的表达式,而只需求函数在每个 权值
w
w
w处的梯度值。
数值梯度的方法,就人为地设置了一个确定的微小值
h
h
h,比如
1
0
−
5
10^{-5}
10−5(具体根据实际需要)。
l
o
s
s
g
=
l
o
s
s
(
w
+
h
)
−
l
o
s
s
(
w
−
h
)
2
h
loss_ g = {loss(w+h)-loss(w-h) \over 2h}
lossg=2hloss(w+h)−loss(w−h)
因此,我们更新
w
w
w 的方式,就像是先试探着往一个方向走一小步,如果发现合适,就再往那个方向走一大步;否则,就往反方向走。
5. 梯度下降中的小批量
小批量随机梯度下降法是机器学习中一种常用的方法,为什么要用到小批量?
前面每次计算损失,都是计算模型函数关于整个样本数据集的损失。那么在样本数据很大时,比如十万、百万的数据量时,这样计算资源的消耗就太大了,而且是不必要的。
使用小批量,就是起到部分代表整体的作用。我们假装一个小批量,就体现着整个数据集的特征。然而这难免有些片面性,通过小批量所指引的
w
w
w 前进的方向,有可能从整个的数据集中来看并不是恰当的方向。因此,我们把一个数据集划分成许多个小批量后,每个小批量都会使用,且会进行多轮(多个周期)的训练,以将整个数据集的特征都充分展现出来。
感谢阅读
版权归原作者 清风莫追 所有, 如有侵权,请联系我们删除。