目录
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。
🚀详情:机器学习强基计划
在什么是机器学习?和AI有什么关系?中我们提到机器学习是致力于研究如何通过计算的手段,利用经验产生模型以改善系统自身性能的学科。数据集核心知识串讲,构造方法解析讲解了数据(经验)的相关概念,本节我们讨论一下机器学习模型的思想。
1 奥卡姆剃刀原则
模型也称为关于真相的**假设(hypothesis),在不考虑性能和准确性的情况下,可以从数据集得到关于真相的多个假设,全体假设的集合称为假设空间(hypothesis space)**。
假设或模型的表示一旦确定,假设空间及其规模随即确定。

假设空间中符合训练集模式的假设论断的集合称为**版本空间(version space)**。由于版本空间的所有假设都导致了关于训练集数据的正确论断,因此这种等效性会使机器学习算法产生输出不确定性——可能版本空间的假设A判断新样本为正例而假设B判断为反例。
所以任何有效的机器学习算法必定要倾向于选择版本空间中的某类假设,称为**归纳偏好(inductive bias)**,归纳偏好可看作对假设空间执行搜索的启发式。
上面的概念有点抽象,老规矩,我们来一个实例。
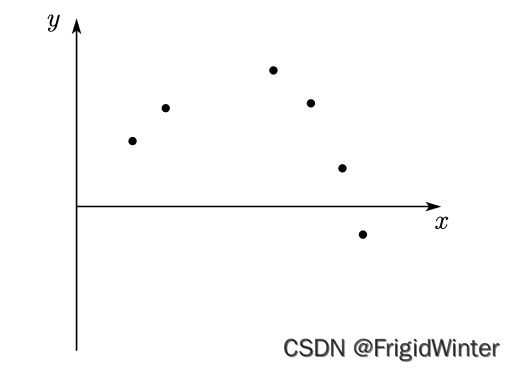
在二维平面上有这样一系列数据样本,我们需要建立一个模型,找出数据的规律
我们不妨选定一个模型的形式,设为多项式模型
y
=
∑
i
=
0
n
a
i
x
i
y=\sum_{i=0}^n{a_ix^i}
y=i=0∑naixi
则我们称全体多项式函数构成该问题的假设空间,假设空间中有许多符合样本分布规律的曲线共同构成版本空间,比如下面这样
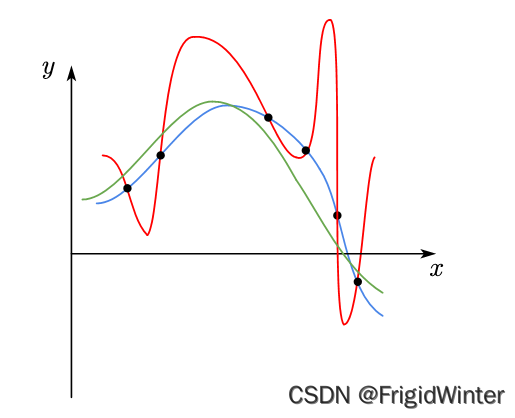
我们可以认为这些不同的曲线都是这个数据集的模型,基于这些模型都可以进行预测。
但是最终我们不能把这么多模型都提交给用户让他们自己选,所以就引出了之前介绍的归纳偏好,我们必须对某一种模型有偏好,才能决断出最终采用什么模型
奥卡姆剃刀原则就是一种归纳偏好,给我们决断模型提供了方向,用一句话概括:
如无必要,勿增实体
即若有多个与观察一致的假设,应选最简单的那个。
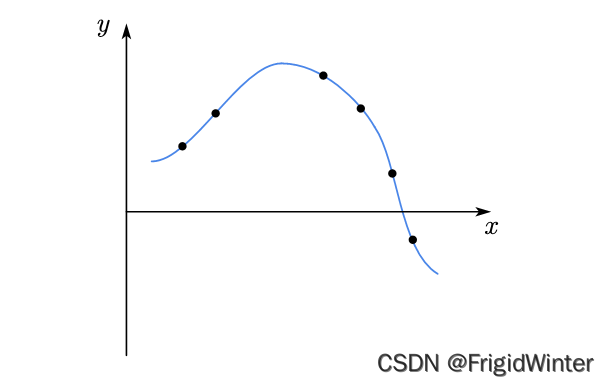
在这个实例中,我们可以选多项式次数最低的那条曲线作为最后的模型
2 天下没有免费的午餐
天下没有免费的午餐教育我们凡事都有代价的道理。那么机器学习中没有免费午餐定理讲得是什么呢?
举例:有一个算法A,其某一项性能,比如计算速度提升,得到算法B;那必然有另一项性能下降,比如存储占用加大。算法A和B哪个好?
你能说算法A比算法B更好吗?不能,因为在对计算速度要求高的场景下B好,对存储要求高的场景下A好。所以算法间的性能改善都要付出代价,而算法性能对比不能脱离实际意义。
现在我们形式化地给出没有免费午餐定理的具体内容:在所有问题出现的概率相同的情况下,任意两个算法间的期望性能相同。
来简单证明下这个定理。
假设样本空间为
X
\mathcal{X}
X,训练集为
X
X
X,则测试集为
X
−
X
\mathcal{X}-X
X−X,其中样本出现概率记为
P
(
x
)
P\left( \boldsymbol{x} \right)
P(x)。设算法为
L
\mathfrak{L}
L,我们要怎么度量这个算法的性能?可以用在测试集上的预测误差来计算
E
o
t
e
(
L
∣
X
,
f
)
E_{ote}\left( \mathfrak{L} |X, f \right)
Eote(L∣X,f)
其中
f
f
f是样本空间中不以人的意志为转移的客观模型,上面这个式子直译过来就是:在给定客观样本空间和有限训练集的情况下,得到算法的期望性能。
我们用全概率公式展开
E
o
t
e
(
L
∣
X
,
f
)
=
∑
h
∑
x
∈
X
−
X
P
(
x
)
ℓ
(
h
(
x
)
≠
f
(
x
)
)
P
(
h
∣
X
,
L
)
E_{ote}\left( \mathfrak{L} |X, f \right) =\sum_h{\sum_{\boldsymbol{x}\in \mathcal{X} -X}{P\left( \boldsymbol{x} \right) \ell \left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right) P\left( h|X, \mathfrak{L} \right)}}
Eote(L∣X,f)=h∑x∈X−X∑P(x)ℓ(h(x)=f(x))P(h∣X,L)
其中
ℓ
\ell
ℓ是性能度量函数,
h
h
h是给定算法和训练集后训练出的模型,
ℓ
(
h
(
x
)
≠
f
(
x
)
)
\ell \left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right)
ℓ(h(x)=f(x))就是模型预测和真实情况不相等时的代价。
回顾一下上面的例子,现实情况中可能有的问题对计算速度要求高,有的对存储性能要求高,换句话说,所有问题都有可能出现,且出现的概率相同,因此针对每种问题的样本空间的
f
f
f也存在若干种等概可能,我们对这些可能性求和(也就是求期望)
∑
f
E
o
t
e
(
L
∣
X
,
f
)
=
∑
f
∑
h
∑
x
∈
X
−
X
P
(
x
)
ℓ
(
h
(
x
)
≠
f
(
x
)
)
P
(
h
∣
X
,
L
)
\sum_f{E_{ote}\left( \mathfrak{L} |X, f \right)}=\sum_f{\sum_h{\sum_{\boldsymbol{x}\in \mathcal{X} -X}{P\left( \boldsymbol{x} \right) \ell \left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right) P\left( h|X, \mathfrak{L} \right)}}}
f∑Eote(L∣X,f)=f∑h∑x∈X−X∑P(x)ℓ(h(x)=f(x))P(h∣X,L)
变换一下积分顺序
∑
f
E
o
t
e
(
L
∣
X
,
f
)
=
∑
x
∈
X
−
X
P
(
x
)
∑
h
P
(
h
∣
X
,
L
)
∑
f
ℓ
(
h
(
x
)
≠
f
(
x
)
)
\sum_f{E_{ote}\left( \mathfrak{L} |X, f \right)}=\sum_{\boldsymbol{x}\in \mathcal{X} -X}{P\left( \boldsymbol{x} \right) \sum_h{P\left( h|X, \mathfrak{L} \right) \sum_f{\ell \left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right)}}}
f∑Eote(L∣X,f)=x∈X−X∑P(x)h∑P(h∣X,L)f∑ℓ(h(x)=f(x))
不失一般性考虑二分类问题,则
∑
f
ℓ
(
h
(
x
)
≠
f
(
x
)
)
=
1
2
ℓ
(
h
(
x
)
≠
f
(
x
)
)
+
1
2
ℓ
(
h
(
x
)
=
f
(
x
)
)
=
σ
\sum_f{\ell \left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right)}=\frac{1}{2}\ell \left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right) +\frac{1}{2}\ell \left( h\left( \boldsymbol{x} \right) =f\left( \boldsymbol{x} \right) \right) =\sigma
f∑ℓ(h(x)=f(x))=21ℓ(h(x)=f(x))+21ℓ(h(x)=f(x))=σ
是一个定值。
结果就是
∑
f
E
o
t
e
(
L
∣
X
,
f
)
=
σ
∑
x
∈
X
−
X
P
(
x
)
\sum_f{E_{ote}\left( \mathfrak{L} |X, f \right)}=\sigma \sum_{\boldsymbol{x}\in \mathcal{X} -X}{P\left( \boldsymbol{x} \right)}
f∑Eote(L∣X,f)=σx∈X−X∑P(x)
其性能与算法本身无关。
最后,总结一下没有免费的午餐定理:脱离具体应用场景空谈学习算法的优劣毫无意义,归纳偏好是否与当前问题匹配直接决定了算法能否取得好的性能。
3 丑小鸭定理
丑小鸭定理问了一个问题:
你觉得是丑小鸭和白天鹅的区别大,还是白天鹅与另一只白天鹅的区别大?
从形态角度,丑小鸭和白天鹅的区别大;从基因角度,白天鹅与另一只白天鹅的区别大!
这说明什么?
说明让计算机自动客观地为我们进行机器学习任务是不可能的,我们必须为它设定一个评判标准,比如丑小鸭问题中,标准是形态比较还是基因比较。而只要引入评判标准,就一定是主观的。
所以这个世界的任何评判都无法做到不歧视的完全公正。
在机器学习中,任何算法都有其主观性,因此对于客观规律的把握总有可改进的空间。
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇
版权归原作者 Mr.Winter` 所有, 如有侵权,请联系我们删除。