池化层是什么?
池化层是深度学习中常用的一种层级结构,它可以对输入数据进行降采样,减少数据量,同时保留重要的特征信息。池化层通常紧跟在卷积层之后,可以有效地减少数据量和计算复杂度,提高模型的训练速度和泛化能力。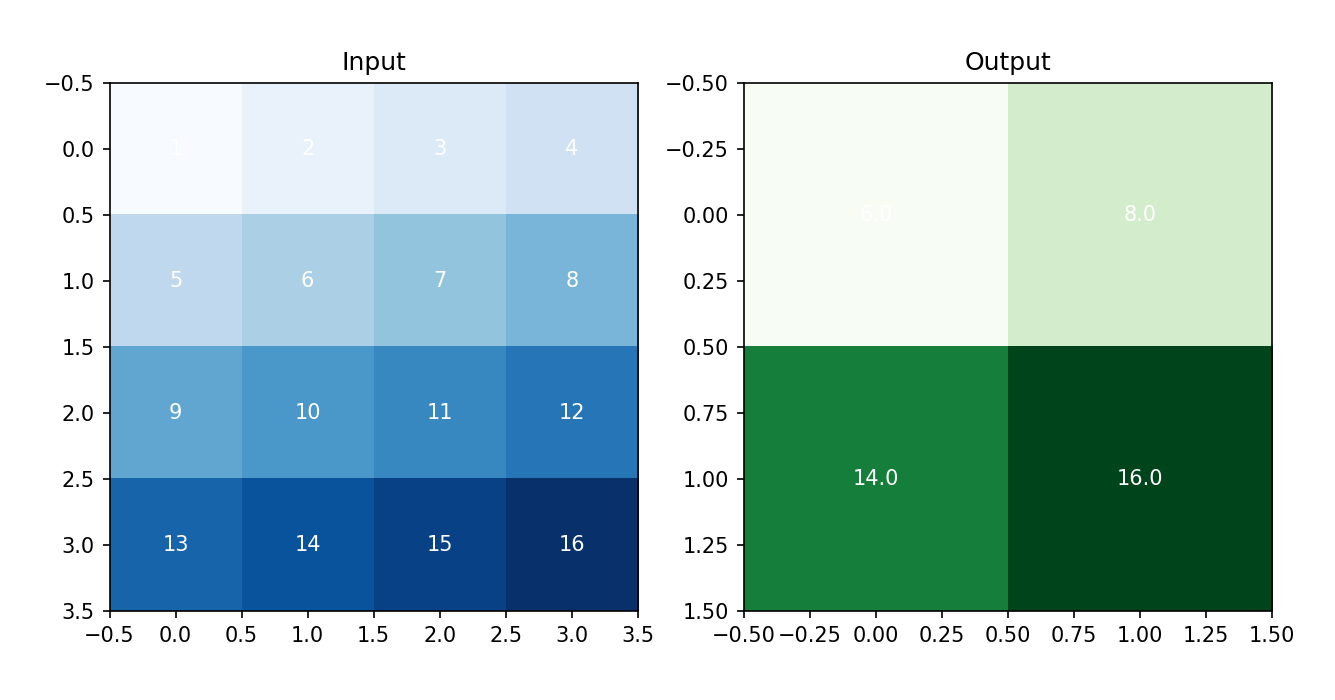
池化层的结构
池化层的结构与卷积层类似,它也由多个滤波器组成,每个滤波器对输入数据进行卷积操作,得到一个输出特征图。不同的是,池化层的卷积操作通常不使用权重参数,而是使用一种固定的池化函数,例如最大池化、平均池化等。
以下是池化层的结构图:
#mermaid-svg-5N236wkQzupBvdTn {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-5N236wkQzupBvdTn .error-icon{fill:#552222;}#mermaid-svg-5N236wkQzupBvdTn .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-5N236wkQzupBvdTn .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-5N236wkQzupBvdTn .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-5N236wkQzupBvdTn .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-5N236wkQzupBvdTn .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-5N236wkQzupBvdTn .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-5N236wkQzupBvdTn .marker{fill:#333333;stroke:#333333;}#mermaid-svg-5N236wkQzupBvdTn .marker.cross{stroke:#333333;}#mermaid-svg-5N236wkQzupBvdTn svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-5N236wkQzupBvdTn .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-5N236wkQzupBvdTn .cluster-label text{fill:#333;}#mermaid-svg-5N236wkQzupBvdTn .cluster-label span{color:#333;}#mermaid-svg-5N236wkQzupBvdTn .label text,#mermaid-svg-5N236wkQzupBvdTn span{fill:#333;color:#333;}#mermaid-svg-5N236wkQzupBvdTn .node rect,#mermaid-svg-5N236wkQzupBvdTn .node circle,#mermaid-svg-5N236wkQzupBvdTn .node ellipse,#mermaid-svg-5N236wkQzupBvdTn .node polygon,#mermaid-svg-5N236wkQzupBvdTn .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-5N236wkQzupBvdTn .node .label{text-align:center;}#mermaid-svg-5N236wkQzupBvdTn .node.clickable{cursor:pointer;}#mermaid-svg-5N236wkQzupBvdTn .arrowheadPath{fill:#333333;}#mermaid-svg-5N236wkQzupBvdTn .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-5N236wkQzupBvdTn .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-5N236wkQzupBvdTn .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-5N236wkQzupBvdTn .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-5N236wkQzupBvdTn .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-5N236wkQzupBvdTn .cluster text{fill:#333;}#mermaid-svg-5N236wkQzupBvdTn .cluster span{color:#333;}#mermaid-svg-5N236wkQzupBvdTn div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-5N236wkQzupBvdTn :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
输入特征图
池化层
输出特征图
池化层的应用
池化层主要用于减少数据量和计算复杂度,同时保留重要的特征信息。它可以提高模型的训练速度和泛化能力,避免过拟合等问题。具体应用包括:
- 图像分类:在卷积神经网络中,池化层常用于减少图像特征的维度,从而提高分类的准确率和速度。
- 目标检测:在目标检测中,池化层可以对特征图进行降采样,从而提高检测的速度和精度。
- 语音识别:在语音识别中,池化层可以降低声学特征的维度,从而提高识别的准确率和速度。
池化层的实现
在PyTorch中,可以使用nn.MaxPool2d和nn.AvgPool2d等函数实现最大池化和平均池化操作。以下是一个简单的例子:
import torch.nn as nn
# 定义一个池化层,使用最大池化函数,池化核大小为2x2,步长为2
pool = nn.MaxPool2d(kernel_size=2, stride=2)# 输入特征图大小为[batch_size, channels, height, width]
input_tensor = torch.randn(1,3,28,28)# 对输入特征图进行池化操作
output_tensor = pool(input_tensor)# 输出特征图大小为[batch_size, channels, height/2, width/2]print(output_tensor.size())
以上代码定义了一个最大池化层,输入特征图大小为[1, 3, 28, 28],输出特征图大小为[1, 3, 14, 14],即将输入特征图的大小降低了一半。
池化层的理论推导
池化层的理论推导与卷积层类似,都是通过卷积操作对输入数据进行处理,得到输出特征图。以下是最大池化和平均池化的推导过程。
最大池化
最大池化是指对输入数据中每个区域内的最大值进行池化操作,得到输出特征图。以下是最大池化的推导过程:
- 定义输入数据和池化核大小
假设输入数据为
X
∈
R
H
×
W
X\in R^{H\times W}
X∈RH×W,池化核大小为
k
×
k
k\times k
k×k,步长为
s
s
s。
- 定义输出特征图
输出特征图
Y
∈
R
H
′
×
W
′
Y\in R^{H'\times W'}
Y∈RH′×W′的大小为:
H
′
=
⌊
H
−
k
s
⌋
+
1
,
W
′
=
⌊
W
−
k
s
⌋
+
1
H'=\left\lfloor\frac{H-k}{s}\right\rfloor+1,\ W'=\left\lfloor\frac{W-k}{s}\right\rfloor+1
H′=⌊sH−k⌋+1, W′=⌊sW−k⌋+1
- 定义最大池化函数
最大池化函数
p
o
o
l
(
X
)
pool(X)
pool(X)的定义为:
p
o
o
l
(
X
)
i
,
j
=
max
m
=
0
k
−
1
max
n
=
0
k
−
1
X
i
×
s
+
m
,
j
×
s
+
n
pool(X)_{i,j}=\max_{m=0}^{k-1}\max_{n=0}^{k-1}X_{i\times s+m,j\times s+n}
pool(X)i,j=m=0maxk−1n=0maxk−1Xi×s+m,j×s+n
其中
i
∈
[
0
,
H
′
)
,
j
∈
[
0
,
W
′
)
i\in[0,H'),j\in[0,W')
i∈[0,H′),j∈[0,W′)。
- 计算输出特征图
将最大池化函数应用于输入数据
X
X
X的每个区域,得到输出特征图
Y
Y
Y:
Y
i
,
j
=
p
o
o
l
(
X
)
i
,
j
Y_{i,j}=pool(X)_{i,j}
Yi,j=pool(X)i,j
其中
i
∈
[
0
,
H
′
)
,
j
∈
[
0
,
W
′
)
i\in[0,H'),j\in[0,W')
i∈[0,H′),j∈[0,W′)。
平均池化
平均池化是指对输入数据中每个区域内的平均值进行池化操作,得到输出特征图。以下是平均池化的推导过程:
- 定义输入数据和池化核大小
假设输入数据为
X
∈
R
H
×
W
X\in R^{H\times W}
X∈RH×W,池化核大小为
k
×
k
k\times k
k×k,步长为
s
s
s。
- 定义输出特征图
输出特征图
Y
∈
R
H
′
×
W
′
Y\in R^{H'\times W'}
Y∈RH′×W′的大小为:
H
′
=
⌊
H
−
k
s
⌋
+
1
,
W
′
=
⌊
W
−
k
s
⌋
+
1
H'=\left\lfloor\frac{H-k}{s}\right\rfloor+1,\ W'=\left\lfloor\frac{W-k}{s}\right\rfloor+1
H′=⌊sH−k⌋+1, W′=⌊sW−k⌋+1
- 定义平均池化函数
平均池化函数
p
o
o
l
(
X
)
pool(X)
pool(X)的定义为:
p
o
o
l
(
X
)
i
,
j
=
1
k
2
∑
m
=
0
k
−
1
∑
n
=
0
k
−
1
X
i
×
s
+
m
,
j
×
s
+
n
pool(X)_{i,j}=\frac{1}{k^2}\sum_{m=0}^{k-1}\sum_{n=0}^{k-1}X_{i\times s+m,j\times s+n}
pool(X)i,j=k21m=0∑k−1n=0∑k−1Xi×s+m,j×s+n
其中
i
∈
[
0
,
H
′
)
,
j
∈
[
0
,
W
′
)
i\in[0,H'),j\in[0,W')
i∈[0,H′),j∈[0,W′)。
- 计算输出特征图
将平均池化函数应用于输入数据
X
X
X的每个区域,得到输出特征图
Y
Y
Y:
Y
i
,
j
=
p
o
o
l
(
X
)
i
,
j
Y_{i,j}=pool(X)_{i,j}
Yi,j=pool(X)i,j
其中
i
∈
[
0
,
H
′
)
,
j
∈
[
0
,
W
′
)
i\in[0,H'),j\in[0,W')
i∈[0,H′),j∈[0,W′)。
池化层的计算步骤
以下是最大池化和平均池化的计算步骤。
最大池化
假设输入数据为
X
∈
R
H
×
W
X\in R^{H\times W}
X∈RH×W,池化核大小为
k
×
k
k\times k
k×k,步长为
s
s
s。
- 定义输出特征图大小
输出特征图
Y
∈
R
H
′
×
W
′
Y\in R^{H'\times W'}
Y∈RH′×W′的大小为:
H
′
=
⌊
H
−
k
s
⌋
+
1
,
W
′
=
⌊
W
−
k
s
⌋
+
1
H'=\left\lfloor\frac{H-k}{s}\right\rfloor+1,\ W'=\left\lfloor\frac{W-k}{s}\right\rfloor+1
H′=⌊sH−k⌋+1, W′=⌊sW−k⌋+1
- 定义输出特征图
初始化输出特征图
Y
Y
Y为
Y
=
0
∈
R
H
′
×
W
′
Y=0\in R^{H'\times W'}
Y=0∈RH′×W′。
- 计算输出特征图
对于每个输出特征图的位置
(
i
,
j
)
(i,j)
(i,j),计算输入数据
X
X
X中对应区域内的最大值,得到输出特征图
Y
Y
Y:
Y
i
,
j
=
max
m
=
0
k
−
1
max
n
=
0
k
−
1
X
i
×
s
+
m
,
j
×
s
+
n
Y_{i,j}=\max_{m=0}^{k-1}\max_{n=0}^{k-1}X_{i\times s+m,j\times s+n}
Yi,j=m=0maxk−1n=0maxk−1Xi×s+m,j×s+n
其中
i
∈
[
0
,
H
′
)
,
j
∈
[
0
,
W
′
)
i\in[0,H'),j\in[0,W')
i∈[0,H′),j∈[0,W′)。
平均池化
假设输入数据为
X
∈
R
H
×
W
X\in R^{H\times W}
X∈RH×W,池化核大小为
k
×
k
k\times k
k×k,步长为
s
s
s。
- 定义输出特征图大小
输出特征图
Y
∈
R
H
′
×
W
′
Y\in R^{H'\times W'}
Y∈RH′×W′的大小为:
H
′
=
⌊
H
−
k
s
⌋
+
1
,
W
′
=
⌊
W
−
k
s
⌋
+
1
H'=\left\lfloor\frac{H-k}{s}\right\rfloor+1,\ W'=\left\lfloor\frac{W-k}{s}\right\rfloor+1
H′=⌊sH−k⌋+1, W′=⌊sW−k⌋+1
- 定义输出特征图
初始化输出特征图
Y
Y
Y为
Y
=
0
∈
R
H
′
×
W
′
Y=0\in R^{H'\times W'}
Y=0∈RH′×W′。
- 计算输出特征图
对于每个输出特征图的位置
(
i
,
j
)
(i,j)
(i,j),计算输入数据
X
X
X中对应区域内的平均值,得到输出特征图
Y
Y
Y:
Y
i
,
j
=
1
k
2
∑
m
=
0
k
−
1
∑
n
=
0
k
−
1
X
i
×
s
+
m
,
j
×
s
+
n
Y_{i,j}=\frac{1}{k^2}\sum_{m=0}^{k-1}\sum_{n=0}^{k-1}X_{i\times s+m,j\times s+n}
Yi,j=k21m=0∑k−1n=0∑k−1Xi×s+m,j×s+n
其中
i
∈
[
0
,
H
′
)
,
j
∈
[
0
,
W
′
)
i\in[0,H'),j\in[0,W')
i∈[0,H′),j∈[0,W′)。
希望以上内容能够帮助您理解池化层的概念和应用,如有疑问请随时提出。
版权归原作者 Helloworld188888 所有, 如有侵权,请联系我们删除。